![]()
|
"...Mentre una singola persona è un intrico incomprensibile, nell’aggregato diventa una certezza matematica. O almeno così dice la statistica." Arthur Conan Doyle |
.
9.1 Nello spazio delle velocità
Nel capitolo precedente noi non abbiamo fatto alcuna ipotesi sulla distribuzione delle velocità nei gas, né abbiamo ricavato alcuna informazione su di essa, al di là del legame tra temperatura assoluta T e velocità quadratica media < v >. La deduzione di tale distribuzione è alquanto laboriosa, e fu compiuta per la prima volta dal grande fisico scozzese James Clerk Maxwell (1831-1879), per cui oggi è nota con il suo nome. È utile vedere come egli procedette, in modo da constatare l'utilità del ragionamento matematico anche in Fisica, accanto all'indagine sperimentale, per lo studio dei fenomeni naturali. Sarà indispensabile fare un uso pesante degli strumenti dell'Analisi Matematica; per questo chi non li possiede deve saltare necessariamente alle conclusioni.
Vogliamo dunque determinare la densità di probabilità y(v), cioè la funzione che, moltiplicata per dv, fornisce la probabilità che una molecola presa a caso abbia velocità compresa tra v e v + dv. Le ipotesi di base sono:
a)
l'indipendenza della distribuzione di velocità dalla direzione;
b) il legame tra velocità quadratica media delle molecole e temperatura del gas,
espressa dalla formula (8.12):
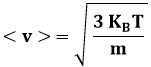
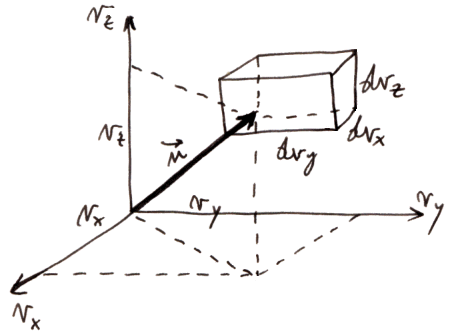
Def. 9.1: Dicesi spazio delle velocità Sv lo spazio tridimensionale i cui punti sono in corrispondenza biunivoca con i vettori delle velocità delle molecole. Le coordinate di ogni punto di sono cioè le componenti vx, vy, vz del vettore v corrispondente.
Prendiamo allora in considerazione un volumetto infinitesimo dτ dello spazio , i cui spigoli sono dvx, dvy e dvz, e posto a distanza dall'origine degli assi pari a:
![]()
Il volumetto non viene indicato con dV proprio per distinguerlo dal "volume" propriamente detto, che si ottiene moltiplicando tre lunghezze, mentre dτ si ottiene moltiplicando tre velocità.
La probabilità dp che una molecola scelta a casaccio nel gas rarefatto abbia velocità v contenuta in dτ, per la legge della composizione degli eventi indipendenti, è pari al prodotto delle probabilità che la componente vx cada nell'intervallo [ vx ; vx + dvx ], che la componente vy cada nell'intervallo [ vy ; vy + dvy ] e che la componente vz cada nell'intervallo [ vz ; vz + dvz ]. Tali probabilità verranno rispettivamente indicate con f(vx) dvx, f(vy) dvy e f(vz) dvz. Ovviamente la funzione f ha la stessa forma matematica nei tre casi, per via dell'ipotesi di isotropia (le direzioni degli assi cartesiani sono del tutto equivalenti fra di loro). Si ha allora:
dp = f(vx) f(vy) f(vz) dvx dvy dvz
Ora, l'ipotesi a) fatta all'inizio è sufficiente per stabilire la forma della funzione f incognita. Infatti, l'unico modo nel quale il prodotto appena scritto può dipendere dalla somma v2 = vx2 + vy2 + vz2 è attraverso un logaritmo, perché:
ln [f(vx) f(vy) f(vz)] = ln f(vx) + ln f(vy) + ln f(vz)
Ma, se la somma di tre funzioni di variabili tra loro indipendenti è legata alla somma dei logaritmi di tali variabili, deve essere per forza:
ln
f(vx)
= A vx2
+ B
ln f(vy)
= A vy2
+ B
ln f(vz)
= A vz2
+ B
Infatti, sommando membro a membro, il fattore A può essere portato a fattor comune:
ln f(vx) + ln f(vy) + ln f(vz) = A ( vx2 + vy2 + vz2 ) + 3 B
e quindi:
ln [f(vx) f(vy) f(vz)] = A v2 + 3 B
Chiamo e3 B = C ed ho:
![]()
e quindi:
![]()
Ora, la probabilità y(v) dv è pari alla probabilità che il vettore velocità di una molecola scelta a casaccio abbia modulo compreso tra v e v + dv, e cioè che il punto che lo rappresenta nello spazio delle velocità cada nell'intercapedine I tra due sfere centrate nell'origine degli assi, e di raggi rispettivamente v e v + dv:
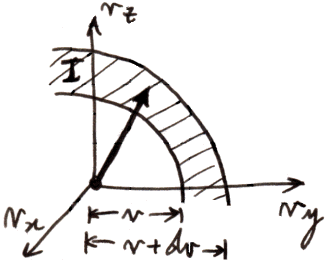
Dunque, y(v) dv è dato dall'integrale della probabilità dp su questo dominio I:
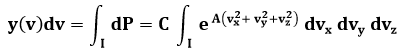
Ma, a meno di infinitesimi, l'argomento dell'integrale è costante e pari all'esponenziale di A v2. Ne segue:
![]()
Tale integrale è pari al volume (nello spazio delle velocità) dell'intercapedine sferica, che può essere espresso moltiplicando la sua area per il suo spessore, cioè con la formula 4 π v2 dv:
Abbiamo così trovato la forma analitica della distribuzione di Maxwell. Non resta che calcolare le costanti A e C. Per questo occorrono due condizioni. La prima è la condizione di normalizzazione, la seconda è l'ipotesi b) sopra scritta. Deve cioè essere:
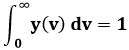
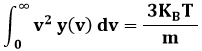
In altre parole, deve risultare:
La (9.3) discende dalla (8.11). Integriamo ora per parti. Nella (9.2) pongo:
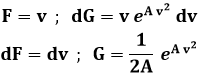
Dunque l'integrale (9.2) dà:
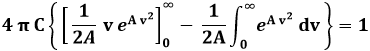
La parentesi quadrata è infinita, a meno che A non sia negativo. In tale ipotesi, si ha:
Questo integrale si calcola in coordinate polari. Basta scrivere:
![]()
Ricordiamo che, per passare da coordinate cartesiane a coordinate polari, queste sono le formule:
![]()
L'integrale sopra scritto è esteso a tutto il primo quadrante. Ne segue che:
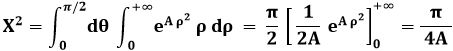
Questo è vero solo se A < 0, come già supposto sopra. Di conseguenza:
![]()
Per cui la (9.4) fornisce:
![]()
e di conseguenza:
Quanto al calcolo di A, dalla (9.3) segue:
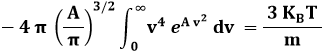
Pongo ora:
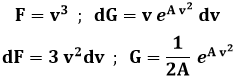
ed ottengo:
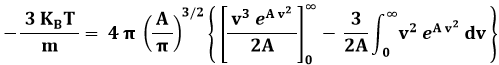
Se A < 0, la parentesi quadrata si elide e resta:
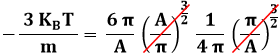
Da cui:
![]()
Dalla (9.5) segue:
![]()
Se sostituisco nella distribuzione (9.1) da noi trovata, ottengo:
Essa viene chiamata la distribuzione di Maxwell, o più semplicemente maxwelliana.

James Clerk Maxwell (1831-1879)
.
9.2 La forma della maxwelliana
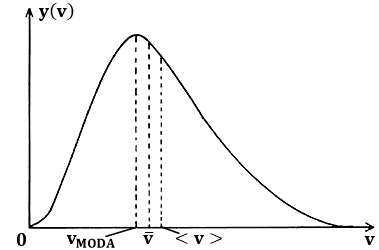
La (9.6) ci dice che, mentre (in linea di principio) tutte le velocità delle molecole sono possibili, è però vero che non tutte risultano ugualmente probabili. Rappresentando le distribuzioni a diverse temperature, si ottengono i grafici seguenti:
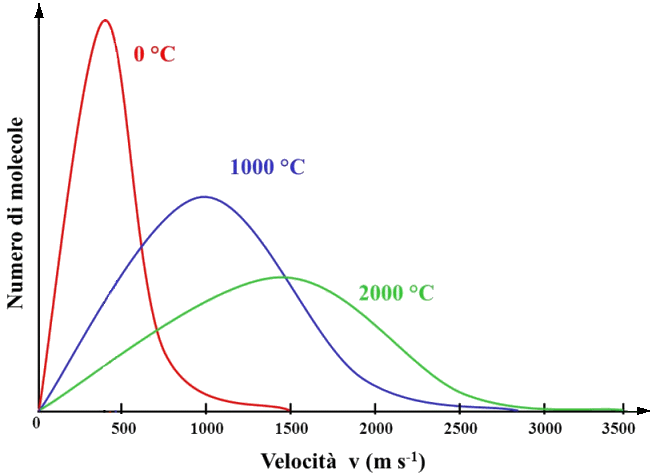
Come si vede, questa curva ha un massimo, è rapidamente crescente prima di questo, e decresce meno rapidamente dopo di esso. Al crescere della temperatura, il massimo si abbassa e tende a spostarsi verso temperature maggiori: ciò corrisponde a quanto già sappiamo circa il legame tra l'agitazione termica e la temperatura. L'ascissa di tale massimo, detta la moda della distribuzione della velocità, è facilmente calcolabile uguagliando a zero la derivata della (9.6); facendolo, si ottiene:
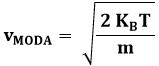
Dalla (8.11) si ricava:
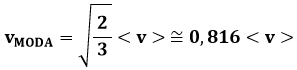
La moda è la velocità più probabile, e non coincide con la velocità quadratica media, ma è pari all'82 % di essa. Tale valore non coincide neppure con il valor medio della velocità, perchè la distribuzione non è simmetrica. Adoperando il formalismo dell'Analisi Matematica, si ha infatti:
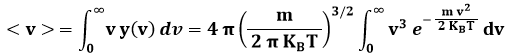
Per trovare v, integriamo per parti, ponendo:
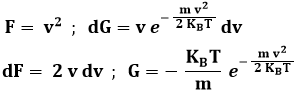
Si ha così:

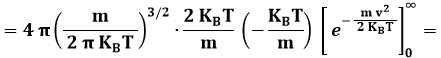
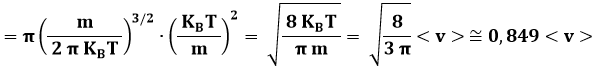
L'ordine crescente vMODA < v < < v > deriva dalla forma asimmetrica della curva, che arriva a v = 0 con tangente orizzontale e, per v → ∞, tende all'infinito con tangente orizzontale; tale asimmetria a sua volta è dovuta alla presenza di v2 nella (9.6). A dir la verità, i miei studenti più attenti si saranno accorti che il limite v → ∞ è privo di significato fisico, in quanto le molecole non possono superare la velocità della luce (lo ha stabilito il vecchio Albert Einstein). Il fatto è che il modello utilizzato per dedurre la suddetta distribuzione è interamente basato sulla Fisica Classica. Del resto, però, per valori della temperatura accessibili agli esperimenti, l'inesattezza della curva maxwelliana è del tutto trascurabile. Bisognerebbe salire a temperature di 1022 K, per poter cominciare ad avvertire effetti relativistici!
Come già spiegato, al crescere della velocità le maxwelliane si abbassano e si allargano, il che è un indice della maggiore dispersione delle velocità intorno al valore medio, e quindi un maggior disordine dello spazio delle velocità. Questo spiega, dal punto di vista microscopico, perché un riscaldamento produce un aumento di entropia del gas, giacché aumenta la dispersione nello spazio delle velocità.
La distribuzione di Maxwell è quella che caratterizza in maniera naturale le molecole di un gas. Noi potremo costruire artificialmente una distribuzione diversa, per esempio immettendo nel recipiente solo molecole con una velocità prefissata; però ben presto la situazione verrebbe modificata dagli urti che le molecole subirebbero tra di loro e contro le pareti. Alcune molecole acquisterebbero velocità a scapito di altre, e la distribuzione convergerebbe verso la maxwelliana, che rappresenta la distribuzione più stabile possibile. Infatti si può provare che, fissata l'energia notale ed il numero di particelle, tra tutte le distribuzioni possibili, la maxwelliana è "la più disordinata", e quindi la più probabile. E, come sappiamo, all'equilibrio in natura si manifesta solo ciò che risulta più probabile che si manifesti. Gli scostamenti da questa distribuzione sono del tutto trascurabili. La trasformazione seguita da un gas per portarsi alla distribuzione maxwelliana è tipicamente una trasformazione adiabatica irreversibile, accompagnata da un aumento di entropia.
.
A questo punto dovremmo aver compreso come, ad opera di Maxwell e di Boltzmann, le leggi statistiche, basate sul concetto di velocità, abbiano fatto per la prima volta il loro ingresso nella Fisica. Prima di loro si pensava che tutto fosse regolato da leggi deterministiche, cioè che, a partire da precise condizioni iniziali, si potesse in ogni caso studiare l'evoluzione di un sistema in tutti i particolari; e questo era influenzato anche dall'implicito determinismo insito nelle equazioni della Dinamica e nelle leggi della Gravitazione Universale. Purtroppo, quando dalla dinamica di un sistema di pochi corpi si passa a quella di un sistema formato da un numero sterminato di particelle, cessa ogni certezza deterministica, e le uniche certezze che ci rimangono sono a livello di distribuzioni di probabilità.
Naturalmente, ogni nuova idea che implica una certa rivoluzione concettuale quasi sempre viene accolta con una certa diffidenza; è stato, questo, anche il destino della Relatività di Einstein, a lungo bollata come "fisica giudea". Non poteva essere diversa la sorte delle teorie fondate sulla natura corpuscolare della materia e nell'applicazione ad essa delle leggi statistiche. Esse suscitarono infatti lunghissime discussioni, talora molto accese, fino a che il fisico tedesco Otto Stern (1888-1969) nel 1926 non riuscì a verificare sperimentalmente la bontà della distribuzione di Maxwell, mediante il selettore di velocità da lui stesso messo a punto. Il suo schema è raffigurato qui sotto.
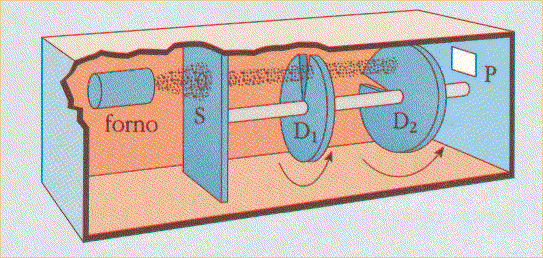
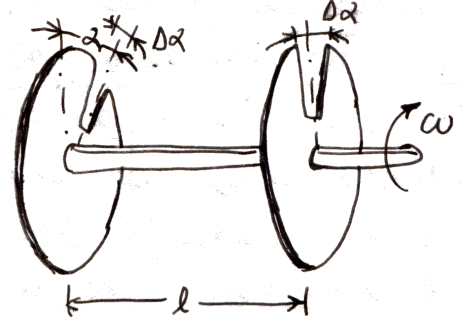
Esso è costituito fondamentalmente da due dischi uguali D1 e D2 calettati sullo stesso albero, entrambi con una fessura radiale di ampiezza Δα, ma calettati in modo che le due fessure siano sfasate di un angolo α. Un forno genera un fascio di atomi di mercurio, che viene iniettato attraverso un collimatore S, così da generare un flusso perfettamente rettilineo e sottile. Esso è poi indirizzato sui due dischi D1 e D2, in rotazione con velocità angolare ω; le molecole che riescono a passare attraverso la fessura del primo disco vengono intercettate dal secondo, a meno che esse non abbiano velocità tale da percorrere la distanza l tra i due dischi nello stesso tempo in cui i dischi ruotano di un angolo Δα, così da "infilare" le due fessure una dopo l'altra. Tale velocità è pari a:
![]()
Variando la velocità ω, varia la velocità v delle molecole che "sopravvivono" al passaggio attraverso i due dischi; un rivelatore P indica la quantità di molecole che possiedono ogni valore di velocità (più esattamente, le molecole la cui velocità è compresa tra v e v + dv). In questo modo, Stern poté verificare che gli atomi di mercurio gassoso obbediscono perfettamente alla distribuzione di Maxwell, fugando una volta per tutte i dubbi residui sulla Teoria Cinetica dei Gas.

Otto Stern (1888-1969)
.
9.4 Il teorema di equipartizione dell'energia
Si è già detto che, nel caso di sistemi privi di moti apparenti, l'energia interna di natura termodinamica si identifica con l'energia meccanica totale (cinetica e potenziale). È semplice scrivere l'espressione di questa energia interna, nel caso di un gas schematizzato secondo il modello da noi utilizzato nello studio della Termodinamica Cinetica. In tal caso, infatti, mancando qualunque interazione diversa dagli urti, l'energia totale si riduce alla sola energia cinetica.
Ora, secondo la teoria statistica, ogni molecola possiede un'energia cinetica pari a 1 / 2 m < v >2. Poiché ogni mole contiene NAV molecole, una massa gassosa composta da n moli di gas conterrà un'energia totale pari a:
![]()
E siccome per la (8.12) si ha:
![]()
ne consegue:
![]()
Ma si è visto nel § 4.6 che, secondo la Termodinamica classica, U = n cV T, e quindi deve essere:
![]()
perchè sappiamo che KB NAV = R. Abbiamo così che il calore specifico molare a volume costante è pari a cV = 3 R / 2, come visto appunto nel § 4.6.
Fin qui, tutto semplice; bisogna però ricordarsi del fatto che il modello da noi utilizzato è fin troppo semplificato. Infatti, nella Teoria Cinetica dei Gas le molecole appaiono come punti materiali, praticamente privi di struttura. Ma l'unico gas reale che si può comportare in questo modo è un gas monoatomico, come l'elio o il neon.
Invece, per un gas biatomico come l'ossigeno, le cose si complicano. Infatti possiamo tentare di schematizzare le molecole come un oggetto formato da due particelle puntiformi, vincolate ad una certa distanza l'una dall'altra. Se ipotizziamo che questa distanza resti fissa, non occorre preoccuparsi delle forze interne alla molecola; trascurando le interazioni tra le molecole, l'energia è ancora puramente di tipo cinetico, però ora le molecole, oltre al contributo traslazionale 1 / 2 m < v >2, ha anche un contributo rotazionale, dovuto alle sue rotazioni attorno al centro di massa. Per cercare di valutare tale contributo, ricorriamo ad un fondamentale assunto della Meccanica Statistica, ottenuto dal solito Boltzmann e noto come:
TEOREMA DI EQUIPARTIZIONE DELL'ENERGIA CINETICA: ad ogni grado di libertà delle molecole è associata, in media, una quantità di energia cinetica pari a KB T / 2.
Naturalmente questo vale in media, ma per un gran numero di particelle possiamo fidarci di esso al 100 %. Vediamo come usarlo.
Se la molecola è monoatomica, come si è supposto finora, ha tre gradi di libertà; e infatti, per individuare la posizione di un oggetto puntiforme, occorrono tre coordinate tra di loro indipendenti. Ne consegue che l'energia cinetica media vale:
![]()
da cui cV = 3 R / 2, come già abbiamo calcolato. Per la molecola biatomica, invece, abbiamo tre gradi di libertà traslazionali e due rotazionali, perchè con tre coordinate si individua il centro di massa, e con due angoli l'asse di inclinazione della molecola! Ne segue:
![]()
e quindi il calore molare a volume costante vale:
![]()

E quindi si ritrova il risultato già noto secondo cui cV = 5 R / 2 per un gas biatomico.
Un risultato del tutto diverso si ottiene però se si ipotizza che la molecola non sia un sistema rigido ma, come avviene in realtà, la distanza tra gli atomi può cambiare. Supponiamo di modellizzare queste forze mediante un'interazione di tipo elastico, supponendo cioè che i due atomi siano collegati da una molla che segue la Legge di Hooke (F = – k x). Sicuramente allora tali atomi oscillano di moto armonico. Infatti, nel moto armonico l'accelerazione ha direzione opposta allo spostamento ed è direttamente proporzionale ad esso. Per il Secondo Principio della Dinamica, F = m a. Sostituendo in essa la Legge di Hooke si ha:
![]()
da cui:
![]()
Per cui il moto delle molecole è armonico. In tale tipo di moto, a = – ω2 x, e quindi:
Usando gli strumenti dell'Analisi Matematica, l'accelerazione è la derivata seconda dello spostamento rispetto al tempo:
![]()
Ponendo perciò:
![]()
Ne risulta:
![]()
![]()
L'energia potenziale del moto armonico è pari a:
![]()
e per la (9.7):
![]()
Mentre quella cinetica è pari a:
![]()
Allora l'energia meccanica totale è pari a:
![]()
Al totale dell'energia cinetica bisogna dunque aggiungere un contributo KB T / 2, dovuto al grado di libertà della distanza interatomica, e poi un ulteriore contributo dovuto all'energia potenziale, ottenendo:
![]()
Da cui si ricava:
![]()
e di conseguenza:
![]()
Per una molecola poliatomica, con gli atomi a distanze fisse, bisogna considerare sei gradi di libertà totali (tre dovuti alle coordinate del centro di massa e tre angoli per l'inclinazione delle molecole nello spazio), per cui:
![]()
da cui U = 3 n R T, e cV = 3 R. A questo punto, è pensabile di applicare la nostra Teoria Cinetica anche alle sostanze solide, rappresentate come atomi puntiformi oscillanti attorno a posizioni di equilibrio, alle quali sono trattenute da forze di richiamo elastico. In questo caso, per ogni atomo vi sono tre contributi di energia cinetica e tre di energia potenziale, per un totale di 6 KB T / 2 = 3 KB T. Allora l'energia interna risulta pari a U = 3 n R T, come nel caso precedente, da cui si inferisce cV = 3 R. Poi, mediante la Relazione di Mayer (4.15), posso trovare i calori specifici a pressione costante cP. Riempiamo allora questa tabella riassuntiva:
| SISTEMA |
MODELLO |
cV |
cp |
| GAS MONOATOMICO | Molecola puntiforme |
|
|
| GAS BIATOMICO | Molecola rigida con cinque gradi di libertà |
|
|
| GAS BIATOMICO | Molecola con vibrazioni elastiche interne |
|
|
| GAS POLIATOMICO | Molecola rigida con sei gradi di libertà |
3 R |
4 R |
| SOLIDO CRISTALLINO | Atomi vincolati elasticamente al cristallo |
3 R |
// |
.
9.5 Validità del modello cinetico
A questo punto, è naturale confrontare i risultati teorici, appena ottenuti secondo la Teoria Cinetica, con quelli sperimentali. A questo scopo, tabuliamo i calori specifici molari a pressione costante (la loro misura è più agevole di quelli a volume costante) in funzione della temperatura per i seguenti gas: elio, vapori di sodio, idrogeno, ossigeno e vapori di litio.

Nel diagramma si è indicato:
con 1 il modello classico di gas monoatomico con tre gradi di libertà;
con 2 il modello classico di gas biatomico con cinque gradi di libertà;
con 3 il modello classico di gas biatomico con vibrazioni elastiche e sette gradi di libertà.
Come si vede dal diagramma, per temperature accessibili alla nostra tecnologia l'accordo (in inglese "fit") delle previsioni teoriche con i risultati sperimentali è ottimo per i gas monoatomici, ed in particolare per i gas nobili come l'elio, mentre per i vapori di sodio si ha uno scostamento massimo del 5 % a 3000 K. Per questi gas monoatomici, dunque, il modello adottato di molecole puntiformi senza struttura interna è perfettamente adeguato. In realtà, noi sappiamo benissimo che l'atomo singolo è costituito da un nucleo e da una nuvola elettronica, ed è pertanto in grado di trovarsi in stati differenti di energia. Il successo del semplice modello classico deriva dal fatto che, a queste temperature, gli urti tra le diverse molecole non sono abbastanza intensi da provocare l'eccitazione interna dei loro atomi. L'energia cinetica media di una molecola monoatomica è infatti facilmente calcolabile per mezzo della solita formula (8.12):
![]()
Esprimendo l'energia in elettronVolt, come si fa in Fisica Atomica, si ha che tale energia cinetica a temperatura ambiente vale:
Ec = 1,5 x 1,38 x 10–23 J / K x 300 K = 6,2 x 10–21 J = 0,039 eV
mentre a 3000 K vale:
Ec = 1,5 x 1,38 x 10–23 J / K x 3000 K = 6,2 x 10–20 J = 0,39 eV
Invece, l'energia minima per eccitare atomi di elio e di sodio valgono rispettivamente 20 eV e 2 eV. Per giungere ad eccitare il sodio serve una temperatura pari almeno a:
T = ( 2 Ec ) / ( 3 KB ) = 2 x 2 x 1,6 x 10–19 J / ( 3 x 1,38 x 10–23 J / K ) = 15.500 K
e per eccitare l'elio bisogna salire addirittura a:
T = ( 2 Ec ) / ( 3 KB ) = 2 x 20 x 1,6 x 10–19 J / ( 3 x 1,38 x 10–23 J / K ) = 155.000 K
A queste temperature però la materia abbandona lo stato gassoso ed assume l'aspetto di plasma.
Quanto invece alle molecole biatomiche, il modello scelto fornisce previsioni accurate entro l'1 % a 300 K per l'idrogeno e per l'ossigeno; per il primo, addirittura, l'accordo è buono fin oltre i 1000 K. Questo è anche il caso di altri gas comuni come N2, HCl, NO, eccetera. Dunque, a temperatura ambiente le vibrazioni interne di queste molecole risultano pressoché "spente". Al crescere della temperatura, però, l'eccitazione interna delle molecole comincia ad avere luogo, e cp si avvicina piuttosto al modello con vibrazioni elastiche. Per l'idrogeno, questo è vero sopra i 3000 K, per l'ossigeno già a 1500 K, mentre per il litio tali condizioni sono già soddisfatte a temperatura ambiente o poco sopra.
Se però si vuole riprodurre dettagliatamente l'andamento di cp tra l'uno e l'altro modello, la Teoria Cinetica classica deve dichiarare fallimento. Un calcolo più preciso può essere condotto solo per mezzo della Meccanica Quantistica, in grado di descrivere la situazione dinamica interna di atomi e molecole molto meglio del tradizionale oscillatore armonico classico. Di questo problema però riparleremo in un altro ipertesto.
Quanto alle molecole poliatomiche, esse non sono riportate sul diagramma soprastante; qui sotto tuttavia vedrete riportati alcuni valor di cp / R, che non si discostano molto dal valore di 4 R previsto dalla Teoria Cinetica dei Gas.
| GAS |
Tipo di molecola |
cp / R |
| N2O | lineare | 4,45 |
| CO2 | lineare | 4,38 |
| C2H2 | lineare | 4,98 |
| C2H4 | non lineare | 5,00 |
| C2H6 | non lineare | 5,85 |
| H2O | non lineare | 3,99 |
Per ottenere risultati più precisi esiste una legge, che distingue tra di loro le molecole lineari da quelle non lineari. Un esempio di molecola lineare è offerto dall'acetilene o etino (C2H2), la cui formula di struttura può essere così ricostruita attraverso un modellino:

Un esempio di molecola non lineare è invece rappresentato dall'etilene o etene (C2H4), così ricostruibile:

Nei due modellini, le sferette nere rappresentano gli atomi di carbonio, quelle rosse gli atomi di idrogeno.
Le molecole lineari come quella dell'acetilene hanno tutte tre gradi di libertà traslazionali e due rotazionali (quello attorno al loro asse è ininfluente); quanto ai gradi di libertà vibrazionali, una legge semiempirica assicura che essi sono in numero totale pari a ( 3 N – 5 ), dove N è il numero totale di atomi di ogni molecola. Per esempio, l'anidride carbonica (CO2) ha tre atomi per molecola, il che corrisponde a quattro gradi di libertà vibrazionali. Sommandoli ai tre traslazionali e ai due rotazionali, si ottiene un totale di nove gradi di libertà. Li moltiplico per R / 2, come richiede la regola, e trovo 4,5 R, in buon accordo con l'esperienza, come dimostra la tabella soprastante. Per l'acetilene (C2H2) invece abbiamo N = 4, e quindi 3 N – 5 = 7: ben sette gradi di libertà vibrazionali, che sommati ai tre traslazionali e ai due rotazionali danno un totale di 12, e moltiplicandoli per R / 2 si arriva a un totale di 6 R.
Quanto alle molecole non lineari, esse hanno tre gradi di libertà traslazionali e tre rotazionali, a cui però bisogna aggiungere ( 3 N – 6 ) gradi di libertà vibrazionali. La molecola di acqua (H2O) ha tre atomi per molecola, il che corrisponde a tre gradi di libertà vibrazionali. Sommandoli ai tre traslazionali e ai tre rotazionali, si ottiene un totale di nove gradi di libertà. Li moltiplico per R / 2 e arrivo a un totale di 4,5 R, come dimostra la tabella soprastante. Per l'etilene (C2H4) invece abbiamo N = 6, e quindi 3 N – 6 = 12: dodici gradi di libertà vibrazionali, che sommati ai tre traslazionali e ai tre rotazionali danno un totale di 18, e moltiplicandoli per R / 2 troviamo un totale di 9 R. Come si vede, per poter prevedere con precisione questi valori occorre una conoscenza più accurata della struttura interna delle molecole, conoscenza che la Teoria Cinetica dei Gas non può certo fornire.
Quanto infine ai solidi cristallini, per essi vale la nota legge di Dulong e Petit, proposta nel 1819 dai francesi Pierre Louis Dulong (1785-1838) e Alexis Thérèse Petit (1791-1820). Essa è di natura sperimentale, è valida purché i solidi cristallini siano semplici, e afferma al di sopra di una temperatura caratteristica, diversa per ogni sostanza, il calore specifico per grammoatomo a volume costante, detto calore atomico, è pari a circa 6 cal / mol °C, cioè appunto a circa 3 R, come previsto abbastanza discretamente dalla Termodinamica Statistica.
Naturalmente, la Teoria Cinetica dei Gas è valida finché sono accettabili due ipotesi basilari: le dimensioni trascurabili delle molecole e l'inesistenza di forze intermolecolari. Tali ipotesi sono valide se il gas è rarefatto e molto lontano dalla temperatura di condensazione, ma se queste condizioni non sono soddisfatte, ci troviamo in condizioni di grande affollamento molcolare, e gli assunti base dell'intera Termodinamica Statistica non sono più validi. Bisogna fare delle ipotesi semplificative per descrivere le forze intermolecolari e per tenere conto del volume proprio delle molecole. Proprio introducendo queste nuove ipotesi l'olandese Johannes Diderik van der Waals (1837-1923) elaborò nel 1873 l'Equazione di Van der Waals (3.4), che noi abbiamo già presentato nel § 3.5, e che è anch'essa "figlia" di una costola della Teoria Cinetica.
.
9.6 La distribuzione di Bose-Einstein
Quanto abbiamo discusso finora vale solo se le particelle hanno un comportamento regolato dalla Meccanica Classica. In realtà, noi sappiamo che per le particelle microscopiche valgono leggi affatto diverse, dettate dalla Meccanica Quantistica. In quel che resta di questo capitolo vogliamo dunque discutere come occorre modificare la Distribuzione di Maxwell e Boltzmann nel caso in cui si debba tenere conto anche del comportamento quantistico delle particelle. La trattazione sarà necessariamente stringata e semplificata, vista la complessità dell'argomento, e dovrà far ricorso al Calcolo Combinatorio e all'Analisi Matematica.
La trattazione quantistica delle particelle si applica quando la distanza tra le particelle si avvicina alla loro lunghezza d'onda di de Broglie, cioè alla lunghezza d'onda dell'onda di materia associata alla particella quantistica. Poiché la densità di occupazione degli stati energetici (che in Meccanica Quantistica sono discreti, a differenza della Fisica Classica) dipende dalla temperatura, si hanno comportamenti diversi tra stati ad alta e stati a bassa temperatura, e ciò richiede di conoscere la distribuzione statistica della velocità delle molecole, che sarà necessariamente diversa da quella vista nel capitolo precedente e in quello presente.

Satyendra Nath Bose ed Albert Einstein
La prima distribuzione quantistica la dobbiamo al bengalese Satyendra Nath Bose (1894-1974), che nel 1920 si occupò delle teorie di Albert Einstein, secondo la quale le onde elettromagnetiche sono costituite da particelle chiamate fotoni. Bose tradusse la teoria della relatività generale di Einstein dal tedesco all'inglese, e decise di derivare da considerazioni statistiche la formula della radiazione del corpo nero di Max Planck (1858-1947), ottenuta ipotizzando che la radiazione non scambi energia con la materia in modo continuo, ma solo attraverso pacchetti discreti, detti appunto quanti. Bose, utilizzando le particelle introdotte da Einstein per spiegare l'effetto fotoelettrico, fu in grado di derivare la formula della radiazione, sviluppando una statistica per particelle massicce senza il vincolo della conservazione del numero di particelle. Bose derivò la Legge di Planck relativa alla radiazione proponendo diversi stati per i fotoni; invece dell'indipendenza statistica delle particelle, Bose considerò le particelle come se fossero all'interno di cellette e descrisse l'indipendenza statistica dello spazio delle fasi di tali cellette.
In questo modo, Bose ottenne un risultato di rilievo, individuando una legge statistica in grado di spiegare il comportamento dei fotoni. Tuttavia nessuna rivista europea volle pubblicare il suo articolo "Planck's Law and the Hypothesis of Light Quanta", nel quale descriveva l'effetto fotoelettrico sulla base di considerazioni statistiche, perchè esso sembrava contenere un imbarazzante errore di statistica: in pratica, lanciando due monete, secondo Bose la probabilità di sortire una testa e una croce era pari ad 1 / 3, poiché egli contava tre possibili esiti: testa-testa, testa-croce e croce-croce. In realtà, la probabilità di ottenere una testa e una croce è pari a 1 / 2 perchè, dal momento che le monete sono due distinte, ci sono due eventi che producono una testa e una croce: testa-testa, testa-croce, croce-testa e croce-croce. La probabilità di ottenere una testa e una croce è quindi di due su quattro. L'assunto di base di Satyendra Nath Bose era quindi palesemente sbagliato; eppure, partendo da esso, il matematico bengalese aveva fornito una predizione teorica in accordo con le osservazioni sperimentali. Bose si rese conto che il suo apparente errore avrebbe potuto non essere per niente un errore, visto che era in accordo con il comportamento della Natura. Egli, inizialmente, sostenne che la distribuzione di Maxwell-Boltzmann avrebbe potuto non essere valida per particelle microscopiche, dove le fluttuazioni dovute al principio di indeterminazione di Heisenberg diventano preponderanti. In ogni caso, le riviste di fisica rifiutarono l'articolo di Bose, sostenendo che egli aveva presentato loro un banale errore, e i suoi risultati furono ignorati. Scoraggiato, Bose scrisse ad Albert Einstein in persona, il quale invece si dimostrò subito d'accordo con le sue teorie. I fisici iniziarono a prendere sul serio le idee di Bose solo quando Einstein mandò loro un proprio articolo in accompagnamento a quello di Bose, che fu pubblicato nel 1924.
Secondo Einstein, poiché i fotoni sono indistinguibili tra loro, non si possono considerare diversi due fotoni aventi la medesima energia. In analogia al lancio delle monete, se paragonassimo un fotone alle monete dell'esempio sopra fatto, la probabilità di ottenere due teste sarebbe una su tre. Il famoso "errore" di Bose è oggi alla base di quella che chiamiamo la distribuzione di Bose-Einstein. Einstein applicò la stessa idea a tutte le particelle con spin intero (in unità h/2π), di cui i fotoni sono un esempio; per questo oggi tali particelle sono chiamate bosoni, in onore di Bose. Applicando questa distribuzione agli atomi, i due fisici predissero l'esistenza di un nuovo, esotico stato della materia, chiamato condensato di Bose-Einstein, la cui esistenza è stata sperimentalmente dimostrata nel 1995, e del quale abbiamo già parlato in precedenza, nel § 5.6.
La distribuzione di Bose-Einstein è descritta dalla formula:
con Ei > μ. In essa, ni è il numero medio di particelle nello stato i, Ei è l'energia dell'i-esimo stato, μ è il potenziale chimico, KB è la costante di Boltzmann e T è la temperatura assoluta. E quanto a gi? Un qualsiasi numero di bosoni può occupare lo stesso sottolivello, esattamente come testa-croce e croce-testa risultano indistinguibili nella statistica di Bose ed Einstein. Supponiamo che ciascun livello contenga gi sottolivelli distinti, ma tutti con la stessa energia e distinguibili tra loro. Ad esempio, due particelle potrebbero avere momenti diversi e di conseguenza essere distinguibili, ma potrebbero avere la stessa energia. Il valore gi dell’i-esimo livello è chiamato degenerazione di quel livello di energia.
Vediamo ora come può essere ricavata la distribuzione di Bose-Einstein. Supponiamo di avere un certo numero di livelli di energia, contraddistinti dall'indice i, ciascuno avente energia Ei e contenente un totale di ni particelle, mentre gi esprime la degenerazione dello stato i. Sia w(n,g) il numero di modi di distribuire n particelle tra i g sottolivelli di un certo livello energetico. Esiste solo un modo di distribuire le n particelle in un solo sottolivello, per cui w(n,1) = 1. È evidente che esistono invece ( n + 1 ) modi di distribuire n particelle in due sottolivelli, quindi scriveremo:
![]()
Con un semplice ragionamento si può stabilire che il numero di modi di distribuire n particelle in tre sottolivelli è w(n,3) = w(n,2) + w(n − 1,2) + ... + w(0,2), da cui:
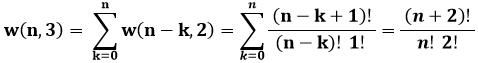
Basta utilizzare la seguente proprietà dei coefficienti binomiali:
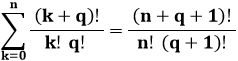
Ripetendo più volte questo procedimento, si può dimostrare che w(n,g) è dato da:
![]()
Generalizzando, il numero di modi di distribuire ni particelle in gi sottolivelli, al variare di i, è il prodotto dei modi in cui ogni livello di energia può essere occupato:
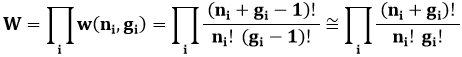
In questa approssimazione si assume che gi >> 1. Seguendo lo stesso procedimento utilizzato per ottenere la statistica di Maxwell-Boltzmann, si dovrebbe determinare un insieme di ni che massimizza la funzione W, sotto il vincolo che il sistema sia costituito da un numero prefissato di particelle e possieda un'energia prefissata. I massimi delle funzioni W e ln W si hanno in corrispondenza del valore Ni. In realtà è meglio rendere massima la funzione scritta qui sotto, perché ciò è matematicamente più semplice da esplicitare, utilizzando il metodo dei moltiplicatori di Lagrange. A questo scopo, si costruisce la funzione:
![]()
Applichiamo la cosiddetta formula di Stirling per i fattoriali:
e teniamo conto dell'approssimazione gi >> 1. Derivando rispetto ad ni, uguagliando a zero e risolvendo rispetto a ni, si ottiene:
![]()
Si può dimostrare, in base a considerazioni di termodinamica, che β = 1 / KB T e α = − μ / KB T. Sostituendo questi valori nella precedente si ottiene la (9.8). Si osservi che la (9.8) si trasforma nella distribuzione di Maxwell-Boltzmann per energie ( Ei – μ ) >> KB T. La distribuzione di Bose-Einstein è fondamentale per il funzionamento del laser.

Salvador Dalì, "La velocità massima della Madonna di Raffaello", 1954
.
9.7 La distribuzione di Fermi-Dirac
La distribuzione di Bose-Einstein non è l'unica distribuzione quantistica conosciuta. I due grandi fisici Enrico Fermi (1951-1954) e Paul Adrien Maurice Dirac (1902-1984), due tra i padri nobili della Meccanica Quantistica, nel 1926 ne introdussero un'altra, detta distribuzione di Fermi-Dirac in loro onore, valida non per i bosoni ma per i fermioni. Queste ultime sono particelle a spin semintero (in unità h/2π) che obbediscono al Principio di Esclusione di Pauli, secondo il quale non possono esistere nello stesso stato quantistico due fermioni aventi gli stessi numeri quantici. In altre parole, i fermioni sono distinguibili fra di loro, a differenza dei bosoni che risultano indistinguibili, Ad esempio, l'elettrone ha uno spin 1 / 2, e quindi è un fermione; esso obbedisce al Principio di Esclusione, e ciò ha una grandissima importanza in vista del cosiddetto aufbau, cioè del "riempimento" dei livelli energetici degli atomi, e quindi della costruzione della Tavola Periodica di Mendeleev. La distribuzione di Fermi-Dirac determina la distribuzione statistica dei fermioni negli stati di energia per un sistema in equilibrio termico. In seguito tale distribuzione fu applicata da Arnold Sommerfeld (1868-1951) anche agli elettroni nei metalli.

Enrico Fermi e Paul Dirac
Consideriamo un esempio semplice per capire le differenze nei conteggi statistici dovuti all'indistinguibilità delle particelle ed al loro carattere bosonico o fermionico. Supponiamo di disporre due particelle in tre scatole differenti. Se le consideriamo distinguibili e le disegniamo l'una colorata di rosso e l'altra di blu, secondo Maxwell e Boltzmann otteniamo nove stati differenti; se le consideriamo indistinguibili tra loro (tutte rosse, ma in modo che non valga il principio di Esclusione di Pauli) otteniamo sei stati differenti; infine, se introduciamo il Principio di Esclusione di Pauli, per il quale due particelle identiche non possono occupare lo stesso stato, allora otteniamo solo tre stati differenti, come mostra la figura seguente:
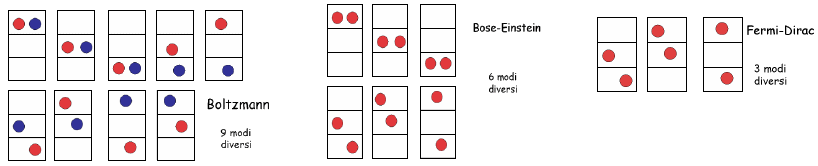
Ricaviamo ora per via statistica la formula della distribuzione di Fermi-Dirac, cioè del numero medio di fermioni che occupano uno stato di singola particella di energia Ei alla temperatura assoluta T:
dove ni è il numero medio di particelle nello stato considerato; Ei è l'energia dello stato considerato; EF è l'energia di Fermi; KB è la costante di Boltzmann e T è la temperatura assoluta.
Come derivare questa distribuzione? Anche in questo caso occorrono il Calcolo Combinatorio e l'Analisi Matematica. Consideriamo un sistema di N fermioni, che possono occupare degli stati quantistici individuati da un gruppo q di numeri quantici, a cui è associata l'energia Eq. Vogliamo determinare il numero medio di fermioni che occupano lo stato q, supponendo che esso dipenda solo da Eq, da N e dalla temperatura assoluta T. A questo scopo, cercheremo la distribuzione che rende massima l'entropia del sistema di N particelle e di energia totale pari ad E, espressa dalla (7.6) (vedi capitolo 7):
![]()
dove P è il numero di stati microscopici che corrispondono a quella distribuzione. Supponiamo di raggruppare tali stati microscopici in gruppi, tali che il gruppo j contiene Gj stati di singola particella e Nj particelle, con Gj >>1 e Nj >> 1, e tuttavia le energie corrispondenti siano molto vicine fra loro e a un'energia "media" Ej. In queste condizioni, il numero medio di occupazione degli stati che appartengono al gruppo j è uguale per tutti, ed è pari a:
nj = Nj / Gj (9.11)
Il numero di modi in cui le Nj particelle possono essere distribuite fra i Gj stati è dato dal numero delle loro combinazioni, che il Calcolo Combinatorio ci insegna essere espresso dal coefficiente binomiale:
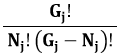
Quindi il logaritmo del numero totale di stati microscopici sarà dato dalla somma di questi contributi per ogni gruppo j:
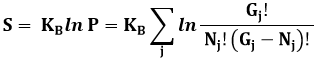
e utilizzando la formula di Stirling (9.9) per il fattoriale otteniamo:
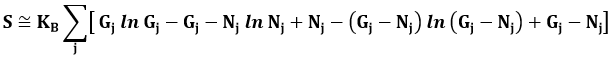
che per la (9.11) diventa:
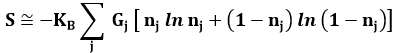
Questa funzione deve essere massimizzata con i vincoli:
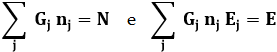
Questo è un problema di massimo con estremo vincolato, che come nel caso della distribuzione di Bose-Einstein si risolve introducendo due moltiplicatori di Lagrange α e β. La soluzione è:
![]()
E risolvendo rispetto a nj si ottiene:
![]()
Anche in questo caso, in base a considerazioni di Termodinamica si ricava β = 1 / KB T e α = EF / KB T. Sostituendo questi valori nella precedente si ottiene la (9.10). Anche quest'ultima si riduce alla distribuzione di Maxwell-Boltzmann per basse energie.
Siccome gli elettroni sono fermioni, gli elettroni dentro un metallo, che sono liberi di muoversi da un atomo all'altro, obbediscono alla distribuzione di Fermi e Dirac; ne consegue che gli elettroni dentro un conduttore si comportano esattamente come le molecole di un gas, come intuì per primo Enrico Fermi nel 1926. Per questo si parla di gas di elettroni di Fermi. Si dice poi energia di Fermi l'energia del più alto livello occupato dal gas di elettroni ad una temperatura molto vicina allo zero assoluto. Detto N il numero di molecole e V il volume occupato dal gas di Fermi, integrando su tutti gli stati si ha:
dove ħ è la costante h/2π. Utilizzando passaggi analoghi a quelli della Teoria Cinetica dei Gas (vedi capitolo 8) si ottiene la pressione esercitata dal gas di Fermi:
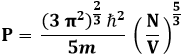
Questa può essere riscritta più semplicemente:
![]()
ed è l'equivalente della Legge di Boyle (vedi § 3.1), secondo cui P V = cost., valida per un gas di molecole classiche.
Consideriamo l'esempio di una nana bianca, una stella collassata con una massa comparabile con quella del nostro Sole, ma con un raggio 100 volte minore, cioè simile a quello della Terra. L'altissima densità raggiunta dalla sua materia fa sì che gli elettroni non siano più legati ai singoli nuclei, ma formino invece un gas elettronico degenerato. La densità elettronica in una nana bianca raggiunge l'ordine di 1036 elettroni/m3. Questo significa che per la (9.12) l'energia di Fermi è pari a circa EF = 5 x 10−14 J = 3 x 105 eV.

Sirio
B, la piccola compagna di Sirio,
è un tipico esempio di nana bianca
Ricapitolando i risultati ottenuti in questo capitolo: la distribuzione di Maxwell-Boltzmann (9.6) si applica ai gas di molecole classiche a temperatura ambiente o a temperature più alte. La distribuzione di Bose-Einstein (9.8) si applica ai gas di bosoni, in stato di degenerazione. La distribuzione di Fermi-Dirac (9.10) si applica ai gas di fermioni, soggetti al principio di Pauli. Quest'ultima distribuzione viene spesso usata per lo studio degli elettroni nei solidi, e quindi costituisce la base per la teoria dei semiconduttori e dell'elettronica, avendo reso possibile scoperte come quella del transistor. La distribuzione di Maxwell-Boltzmann rappresenta il limite classico in condizioni non degeneri e ad alta temperatura delle distribuzioni di Bose-Einstein e di Fermi-Dirac: infatti ad alta temperatura la maggior parte dei sistemi si comporta analogamente a quelli classici, ovvero le differenze tra fermioni e bosoni sono trascurabili a meno che essi abbiano una densità molto alta, come ad esempio appunto in una nana bianca.

E anche stavolta, abbiamo concluso l'ultimo capitolo; vi ringrazio molto per avermi seguito fin qui, nonostante l'oggettiva difficoltà degli argomenti trattati. Tuttavia, anche stavolta desidero aggiungere a questo libro un'Appendice che contiene, per gli studenti interessati, alcuni importanti approfondimenti a livello universitario, che richiedono conoscenze approfondite di Analisi Matematica. Se invece vi sentite pronti a misurarvi con alcuni esercizi conclusivi, cliccate qui. Per tornare all'indice, infine, il link è questo.
![]()