![]()
|
"Oltre la notte, oltre l'invisibile, Genrosso, "Oltre l'invisibile", 1992 |
.
4.1 Il lavoro esterno
Come si è già detto, la Termodinamica studia la complessa fenomenologia che deriva dagli scambi energetici tra un sistema e l'ambiente esterno, con particolare riguardo ale trasformazioni del lavoro in calore e del calore in lavoro. In relazione al suo primo sviluppo storico, infatti, la Termodinamica si è originata come un ramo collaterale della termologia, riguardante le macchine termiche; in seguito però si è rivelata un mezzo d'indagine in grado di analizzare qualunque problema connesso al calore e al lavoro. Vediamo dunque come si è giunti alla formulazione dei principi che stanno alla base della Termodinamica.
Anzitutto, il Principio di Conservazione dell'Energia limitata alle sole forme di energia meccanica (cinetica, elastica, gravitazionale...) non può essere sperimentalmente verificato. Infatti, ad esempio un pendolo sottoposto ad un impulso iniziale dovrebbe oscillare all'infinito, mentre invece a poco a poco le sue oscillazioni si smorzano, finché si ferma, e tutta la sua energia meccanica scompare. Idem dicasi per gli urti anelastici, in cui l'energia meccanica non si conserva affatto.
Insomma, l'energia cinetica tende sistematicamente a diminuire fino ad annullarsi, in tutti i casi in cui sono presenti forze dissipative. Se però tocchiamo i copertoni di un'auto dopo che questa ha frenato, disperdendo così tutta la propria energia cinetica, ci accorgiamo che essi sono caldi. Idem dicasi per le rotaie di un treno dopo che questo ha frenato presso una stazione. Se, in generale, eseguiamo un'esperienza durante la quale una certa quantità di energia meccanica è scomparsa all'interno di un calorimetro, si verifica che il termometro in esso inserito segnala un aumento di temperatura. In tal caso, è evidente che una certa quantità di energia meccanica si è completamente convertita in una quantità misurabile di calore. Viceversa, il calore può, almeno in parte, essere convertito in energia meccanica, come sa chi ha visto i tradizionali film western, dove all'accensione del fuoco nella caldaia del treno corrisponde il movimento delle ruote. Il problema principale che intendiamo affrontare è dunque questo: in che modo il calore si trasforma in lavoro, e viceversa? Come calcolare il lavoro e il calore che intervengono in una determinata trasformazione termodinamica?
Un treno del Far West nel film "Butch Cassidy" (1969) di George Roy Hill
Def. 4.1: Si dice lavoro esterno il lavoro compiuto dalle forze che il sistema esercita sull'ambiente esterno, quando la frontiera del sistema subisce uno spostamento (il lavoro è sempre compiuto da una forza lungo uno spostamento). Per questo, se la frontiera non si sposta, il lavoro è da considerarsi nullo. Naturalmente, esso non comprende:
i) né il
lavoro compiuto dalle forze interne al sistema,
ii) né il lavoro compiuto dalle forze esterne lungo spostamenti di particelle
microscopiche che non muovano la frontiera del sistema.
Il lavoro esterno è dunque una parte del lavoro meccanico totale che si compie durante una trasformazione del sistema, poiché il lavoro meccanico totale comprende anche i contributi (i) e (ii). Tuttavia, il nostro interesse si focalizza unicamente sul lavoro esterno, poiché questo è calcolabile quando sono note le forze (o le pressioni) agenti sulla frontiera e gli spostamenti di questa (o le variazioni di volume), mentre il lavoro meccanico totale richiederebbe un'impossibile conoscenza dettagliata di forze e spostamenti microscopici. Inoltre, visto ciò che abbiamo detto sopra riguardo alle applicazioni tecniche, ciò che interessa di una macchina è connesso allo spostamento macroscopico di parti del sistema, più che a vibrazioni invisibili delle molecole.
Vediamo dunque come calcolare il lavoro esterno in maniera semplice. Supponiamo di prendere un elemento ΔS della frontiera del nostro sistema. Sia F la forza agente su di esso per via delle forze esterne; se pF è la pressione sulla frontiera, avremo:
ΔS = pF ΔS
Usando invece il linguaggio dell'Analisi Matematica, dS sarà l'elemento infinitesimo di area della frontiera, ed allora la forza infinitesima agente su di esso sarà:
dF = pF dS
Convenzione: Si assume come positivo il lavoro compiuto dal sistema sull'ambiente, e negativo quello compiuto dall'ambiente sul sistema.
Se dunque la frontiera subisce uno spostamento Δl, il sistema compie complessivamente sull'elemento di area ΔS un lavoro pari a:
![]()
e in termini infinitesimi:
![]()
Questo è un infinitesimo del terzo ordine, dato che dS è del secondo ordine e dl è del primo ordine. Occorre dunque integrare tre volte per determinare W. Ma ora torniamo a ragionare in termini finiti, ed osserviamo la figura seguente:

θ è l'angolo formato dal vettore Δl con la normale uscente dalla frontiera del sistema nel punto in cui è centrata ΔS. Per ottenere il lavoro esterno complessivo, cioè quello compiuto da tutto l'ambiente esterno su tutto il sistema, bisogna sommare su tutta la frontiera del sistema:

Se pF è costante su tutta la frontiera del sistema, come avviene se la trasformazione è reversibile, ed il sistema è costituito per esempio da un fluido di densità trascurabile, la metto a fattor comune e la porto fuori dalla sommatoria. Dalla figura soprastante si ricava che ΔS Δl cos θ è il volume di un cilindro che ha ΔS come base e Δl come generatrice, per cui si ottiene:
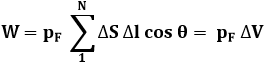
In termini di Analisi Matematica, questo equivale a un integrale doppio. Resta perciò da integrare su l, ma siccome il lavoro è un differenziale non esatto, l'integrazione va condotta lungo tutta la trasformazione. In ogni caso, il risultato non dipende solo dallo stato iniziale A e dallo stato finale B, ma anche dal tipo di trasformazione seguita da A a B. Dunque il lavoro esterno termodinamico non è la variazione di una funzione di stato. Non possiamo cioè inventarci un'energia potenziale, come si fa nel caso del lavoro della forza gravitazionale, della forza elastica o della forza elettrostatica, perchè in quei casi il campo era conservativo. In termini di Analisi Matematica:
Questa è la formula da usare per calcolare il lavoro lungo una trasformazione qualsiasi. Essa però vale solo sotto le seguenti ipotesi:
a) sforzi normali alla
superficie che si sposta;
b) pressione uniforme.
Non servirebbe, per esempio, per calcolare il lavoro di un corpo solido che striscia su di una superficie solida. Inoltre, l'integrale (4.1) è calcolabile solo se riusciamo a sostituire a P una funzione della variabile V, del tipo P = P(V). Nel seguito vedremo come si applica questo calcolo allo studio di particolari trasformazioni, molto utili per risolvere i nostri esercizi.
E per chi non conosce neppure i rudimenti dell'Analisi Matematica? Useremo la cosiddetta integrazione grafica, che ora illustreremo. Il prodotto p dV rappresenta l'area di un rettangolino di altezza P e di base dV nel piano di Clapeyron (colorato in rosso qui sotto); l'integrale (4.1) rappresenta dunque la somma delle aree di tutti i rettangolini sottesi dalla funzione P = P(V), e quindi coincide con l'area del trapezoide compreso tra la curva , l'asse V e le perpendicolari condotte a quest'ultimo da VA e da VB fino alla curva stessa:

Se ne deduce che le aree nel piano PV corrispondono a dei lavori; in particolare, l'area sottesa da una trasformazione termodinamica rappresenta il lavoro compiuto sull'ambiente dal sistema nel corso di tale trasformazione.
Questo permette di visualizzare il fatto che d*W non è un differenziale esatto. Si considerino infatti le due trasformazioni 1 e 2 illustrate qui sotto. Entrambe partono dallo stato A e si concludono nello stato B, però sottendono aree molto diverse, e quindi compiono lavori molto diversi sull'ambiente circostante. Il lavoro di conseguenza non è una funzione di stato.
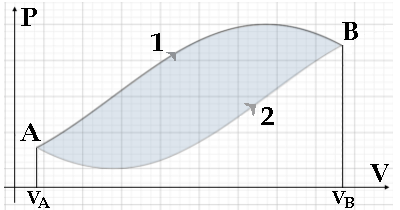
Inoltre, questa rappresentazione ci permette di giustificare la nostra convenzione di segno. Infatti, se il tratto AB è percorso nel verso delle V crescenti (il lavoro è fatto contro l'ambiente: lo stantuffo che si espande), l'integrale è positivo e con esso il lavoro. Se invece il tratto viene percorso in senso contrario, l'area è evidentemente negativa (il lavoro è compiuto dall'ambiente sul sistema: lo stantuffo che scende), e con essa il lavoro. La nostra convenzione è dunque più che giustificata.
Se poi voglio calcolare il lavoro compiuto nel caso di un ciclo, cioè quando punto iniziale e punto finale coincidono, dalla figura di evince che tale area è uguale a quella di ACBB'A' meno quella di AC'BB'A', poiché il tratto ACB è percorso nel senso dei valori crescenti di V, quello BC'A nel senso dei valori decrescenti di V.

Se ne deduce che:
Wciclo = S (ACBB'A') – S (AC'BB'A') = S (ACBC')
In termini di Analisi Matematica si scrive:
![]()
Tale valore è positivo se il ciclo è percorso in senso orario, negativo se è percorso in senso negativo.
.
4.2 Il lavoro lungo alcune particolari trasformazioni
Vediamo ora di utilizzare quanto detto nel paragrafo precedente per calcolare i lavori compiuti durante alcune particolari trasformazioni:
a) ISOCORA. Lungo di essa, V = cost., dunque ΔV = 0. Lo stantuffo del cilindro è bloccato, non può andare né su né giù, e quindi non può compiere lavoro: WV = 0 (la V a pedice indica l'isocora). L'isocora è la trasformazione che avviene senza scambio di lavoro meccanico.
b) ISOBARA. Lungo di essa, P = cost., dunque il lavoro corrisponde all'area di un rettangolo:
WP = P ΔV = P (VB – VA)
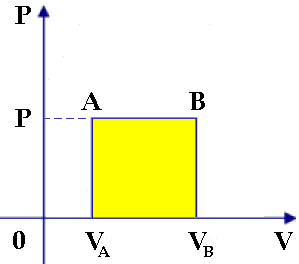
Usando il linguaggio dell'Analisi, basta notare che la pressione è costante e perciò essa esce dall'integrale (4.1):
![]()
Il lavoro in questo caso dipende solo dal volume nei due estremi: WP = P ΔV.
c) ISOTERMA. In questo caso, T = cost. e vale la legge di Boyle P V = cost. Purtroppo calcolare l'area sottesa dall'isoterma con procedimenti elementari è impossibile, e bisogna per forza ricorrere al calcolo integrale. Chi non lo conosce, può saltare subito al risultato La legge di Boyle può essere scritta P V = PA VA, da cui si può ricavare:
![]()
Sostituendolo nella (4.1), otteniamo:

E ricordando che PA VA = PB VB:
che si può anche scrivere:
![]()
Def. 4.2: Si dice politropica una trasformazione che nel piano di Clapeyron è rappresentata dall'equazione:
P Vk = cost. (4.3)
con k numero reale qualsiasi. Se k = 0 si ha P = cost., dunque l'isobara è una politropica. Se k = 1 si ha P V = cost., cioè la legge di Boyle, e dunque anche l'isoterma è una politropica. Invece l'isocora non lo è, perchè non è possibile eliminare la P, ma è il limite a cui tendono le politropiche quando k tende a meno infinito, perchè ogni numero maggiore di 1, se elevato a meno infinito, tende a zero. In seguito vedremo che anche l'adiabatica è una politropica, per k = γ.
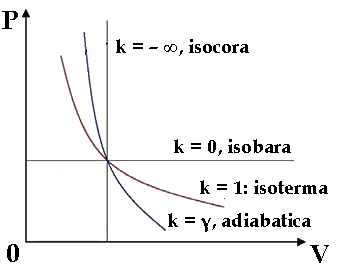
Il lavoro compiuto lungo una politropica può essere calcolato solo con gli strumenti dell'Analisi; anche in questo caso, chi non li possiede salti subito al risultato. Scriviamo anzitutto la politropica in questa forma:
P Vk = PA VAk
Da cui ricaviamo:
![]()
E perciò la politropica di esponente k ha lavoro:

Poiché PA VAk = PB VBk, si ha:
Osserviamo che se k = 0, cioè se mi muovo lungo l'isobara, la precedente diventa:
![]()
che è il risultato già trovato sopra. Se invece k tende a meno infinito, l'equazione della politropica tende a quella dell'isocora; a denominatore della (4.4) si ha allora un infinito e il lavoro tende a zero, in accordo con il calcolo precedente. Solo per l'isoterma la suddetta formula non funziona, perchè sia a numeratore che a denominatore compare uno zero, e l'espressione perde di significato.

Grafico delle trasformazioni politropiche al variare del parametro
4.3 Il Primo Principio dela Termodinamica
Prendiamo in considerazione una trasformazione chiusa, cioè quello che chiameremo un ciclo termodinamico. Per essa dall'esperienza di Jouke già sappiamo che il lavoro compiuto sul fluido dalla trasformazione si cambia integralmente in calore. Se perciò misuriamo il calore in Joule, come il lavoro, per tali sistemi vale l'equivalenza:
Q = W (4.5)
Questa osservazione esprime facilmente il primo principio della termodinamica per trasformazioni chiuse. In pratica, qualunque meccanismo in grado di produrre lavoro in modo continuo, che deve essere necessariamente basato su trasformazioni termodinamiche chiuse, per funzionare ha bisogno di un apporto di calore. Insomma, non è possibile creare lavoro dal nulla. La (4.5) rappresenta perciò una prima forma della conservazione dell'energia. Per avere una forma più completa di tale principio, consideriamo una trasformazione non chiusa, come l'espansione di un gas in uno stantuffo. Introduciamo la seguente:
Convenzione: Il
calore è positivo se è
entrante in un sistema, negativo se uscente.
Invece il lavoro è positivo
se compiuto dal sistema sull'ambiente,
negativo se compiuto
dall'ambiente sul sistema.
Questa convenzione può essere compresa mediante una metafora economica. Il denaro è positivo se è guadagnato ed entra in una casa, è invece negativo se è speso e ne esce. Il lavoro è positivo se io lo compio per conto di un altro e vengo pagato; se invece devo chiamare un idraulico e lui compie un lavoro per conto mio in casa mia, lo devo pagare e tale lavoro è negativo.
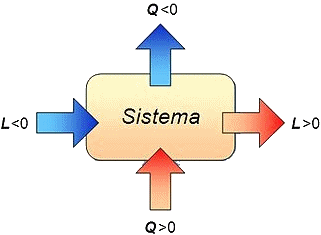
Prendiamo ora in considerazione per es. 1 kg di acqua a 15°C, e portiamo la sua temperatura a 100°C. Tale trasformazione si può eseguire in vari modi. Uno di questi consiste nel fornire le 85.000 calorie necessarie per questa trasformazione riscaldando l'acqua sul fuoco. In questo caso non si compie alcun lavoro meccanico sul sistema, mentre gli vengono cedute 85.000 cal sotto forma di calore. Dunque:
|
Q1 = + 85.000 cal |
Ma c'è anche un'altra possibilità: inserire quel chilo di acqua in un mulinello di Joule e far ruotare le sue pale finché il sistema non raggiunge la temperatura finale. In questo caso però il lavoro è negativo, in quanto è l'ambiente a compiere lavoro sul sistema, mentre il calore scambiato è nullo.
|
Q2 = 0 cal |
Un terzo sistema consiste nel fornire in parte calore e in parte lavoro meccanico; ad esempio, scaldando il chilo d'acqua in modo da fornirgli 35.000 cal di calore ed azionando il mulinello di Joule così da fornirgli 50.000 cal sotto forma di lavoro meccanico:
|
Q3 = + 35.000 cal |
Insomma, la trasformazione può avvenire in infiniti modi. In tutti i casi però la differenza Q – W è costante e non dipende dal tipo di trasformazione. È quindi una funzione dello stato del sistema, e non del tipo di trasformazione. In altre parole, Q – W è una funzione di stato, nonostante né Q né W lo siano. In termini di Analisi Matematica si dice che il differenziale d*Q – d*W è un differenziale esatto.
Ciò suggerisce di introdurre una nuova funzione di stato, analoga all'energia potenziale gravitazionale, elastica ed elettrostatica, che dipende solo dallo stato di un sistema in un determinato istante, in modo che la differenza Q – W sia pari alle variazioni di questa grandezza, ovvero alla differenza tra il suo valore alla fine e quello all'inizio.
Def. 4.3: Una tale variabile di stato si dice energia interna U del sistema.
Essa ha il significato di energia totale del sistema. Per comprendere questo concetto, ritorniamo alla metafora economica. Supponiamo che il sistema sia un'impresa e che il calore sia il denaro di cui essa dispone. L'impresa ha delle entrate (il calore positivo che fluisce nel sistema) e delle uscite (il calore negativo che fluisce fuori di esso); però questo denaro viene impiegato per acquistare materiale dall'esterno (il lavoro negativo fatto sul sistema) e per rivendere prodotti finiti sul mercato (il lavoro positivo fatto sull'ambiente). L'energia interna ha il suo equivalente nel "valore" della merce che effettivamente circola nell'impresa: il denaro ne ha uno, il materiale grezzo un altro, il prodotto finito un altro ancora. All'inizio nell'impresa ho un fondo cassa del valore di 10.000 euro; acquisto materiale grezzo per 2.000 euro e rivendo prodotti finiti per 4.000 euro, spendendo 1.000 euro per sostentamento, abbigliamento e motivi vari. Alla fine il fondo cassa è di 11.000 euro, per cui la variazione complessiva è di + 1.000 euro. Se acquisto materiale per 3.000 euro, ne rivendo per 6.000 euro e ne spendo 2.000 per motivi vari, il guadagno netto è sempre di 1.000 euro.
Se perciò parto dallo stato A, a cui è associato un valore di 10.000 euro, e arrivo allo stato B con un valore di 11.000 euro, mi accorgo che:
|
(4.000 – 2.000) – 1.000 = 1.000 |
cioè la differenza tra valore della merce e valore del denaro è costante: cambia se cambio gli stati A e B, non il tipo di transazione. Analogamente, se UA è l'energia interna dello stato A e UB quella dello stato B, avremo:
Q – W = UB – UA
qualunque siano le trasformazioni in cui si scambiano un calore Q ed un lavoro W, purché gli stati A e B restino gli stessi. Sia Q che W sono forme di energia, ma diverse: U esprime l'energia del sistema in modo astratto dalle sue manifestazioni fenomenologiche (calore e lavoro), esattamente come il "valore" è astratto dal fatto di trattarsi di denaro o di merce.
Possiamo allora enunciare il:
PRIMO PRINCIPIO DELLA TERMODINAMICA: La differenza tra il calore e il lavoro che un sistema scambia con l'ambiente esterno eguaglia la sua variazione di energia interna.
Q – W = ΔU (4.6)
La sua interpretazione più immediata è questa: se l'apporto di calore supera la produzione di lavoro (Q > W), l'energia complessiva "immagazzinata" nel sistema aumenta; nel caso contrario, il sistema si impoverisce di energia, per riportare il bilancio alla pari.
Il Primo Principio esprime dunque la conservazione dell'energia del sistema, esattamente come il bilancio economico fatto prima esprime la conservazione del valore della merce. Inoltre, esso garantisce che il calore è una forma di energia (o, almeno, un modo in cui l'energia si trasmette), e quindi riassume in sé anche il principio di equivalenza. Infatti, se la trasformazione è ciclica, si ha ΔU = 0, perchè stato iniziale e finale coincidono, e quindi Q = W: si ritrova la (4.5). Inoltre, il Primo Principio può essere visto come un'estensione del principio di conservazione dell'energia meccanica a quei fenomeni che coinvolgono scambi di calore. Infatti il principio per il quale la somma tra energia cinetica ed energia potenziale è costante vale solo se le forze in gioco sono conservative, cioè se non viene dispersa energia sotto forma di attrito, ovvero di calore. In questo caso, al principio di conservazione dell'energia meccanica va sostituita la (4.6).
La prima formulazione del Primo Principio della Termodinamica è attribuita al fisico tedesco Julius Robert von Mayer (1814-1878).
.
4.4 Il moto perpetuo di prima specie
Il Primo Principio della Termodinamica è altresì importantissimo perchè permise di negare una volta per tutte la realizzabilità del cosiddetto moto perpetuo.
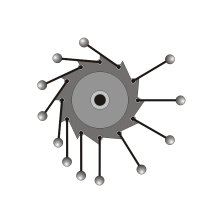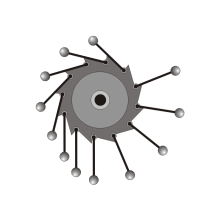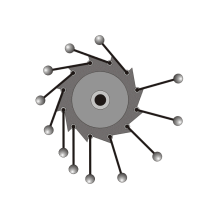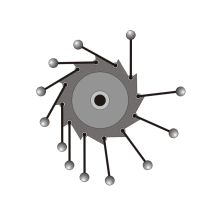
Si dicono macchine a moto perpetuo quegli ipotetici congegni, realizzare i quali era l'obiettivo di molti ingegneri del passato, in grado di creare lavoro utile senza alcuna spesa di energia. Intorno al 1150 il matematico indiano Bhāskara (1114-1185) descrisse una ruota in legno con raggi cavi riempiti di mercurio; poiché da un lato il liquido pesante distava maggiormente dal centro rispetto all'altro, la ruota avrebbe dovuto girare per inerzia all'infinito. Questo fu solo il prototipo di una serie di progetti di macchine, basati su ruote con elementi perennemente sbilanciati e indefinitamente attratti dalla gravità terrestre, come quello progettato nel 1245 dall'architetto francese Villard de Honnecourt, che si vede qui sotto. In esso al disco di legno sono collegati dei pendoli metallici; facendo ruotare il disco in senso antiorario, i pendoli ruotano ricadendo verso sinistra, e lo strappo da essi causato sarebbe sufficiente a vincere la resistenza di quelli sulla destra:

Il famoso Leonardo da Vinci (1452-1519) fu il primo a rendersi conto dell'impossibilità del moto perpetuo, come scrive nel Codice Madrid I:
« Qualunque peso sarà appiccato alla rota, il quale peso sia causa del moto d’essa rota, senza alcun dubbio il centro di tal peso si fermerà sotto il centro del suo polo; e nessuno instrumento che per umano ingegno fabbricar si possa che col suo polo si volti, potrà a tale effetto riparare. [...] O speculatori del continuo moto, quanti vari ingegni in simil cerca avete creati! Accompagnatevi con li cercatori d’oro. » [cioè gli alchimisti, che cercavano la pietra filosofale]
Nonostante il suo parere, gli sforzi per realizzare questa mitologica macchina proseguirono. Uno dei più famosi tentativi di mettere a punto il moto perpetuo è quello risalente al 1618 dell'alchimista inglese Robert Fludd (1574-1637). Esso comprendeva una pompa in grado di sollevare l'acqua che, cadendo, metteva in moto una ruota idraulica in grado di azionare la pompa stessa, come mostra questa incisione d'epoca:

Il gesuita Jean Taisnier (1508-1562) sviluppò una macchina basata sull'attrazione esercitata tra magneti opportunamente disposti su una ruota e schermati da fogli di piombo. Persino Denis Papin (1647-1712), che come abbiamo visto nel § 2.1 è noto come inventore della pentola a pressione, nel 1685 tentò di costruire una macchina a moto perpetuo utilizzando le proprietà dei fluidi:
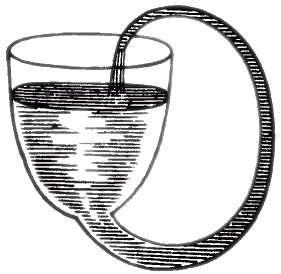
Papin pensava che, grazie alle proprietà dei capillari, l'acqua continuasse a scorrere nel tubo all'infinito. In realtà la stessa forza di coesione che attira il liquido lungo il tubo, impedisce alle goccioline di lasciare la scodella ed il flusso non è perpetuo. Con i fluidi si cimentarono altri che pensarono ad un nastro cui erano appesi dei galleggianti, metà dei quali erano immersi in acqua; si pensava che i galleggianti venissero in superficie attraverso il liquido per via del Principio di Archimede e facessero girare il nastro in eterno; tuttavia il piazzamento dei galleggianti sul fondo richiedevapiù energia di quanta essi generano risalendo.
Anche se oggi la cosa può sembrare risibile, una simile chimera è stata l'idea fissa di molti ancora in tempi recenti, tanto che ancor oggi vi è chi deposita brevetti di presunte macchine per il moto perpetuo. Il miraggio del moto perpetuo ha però suggestionato tutti gli uomini, compresi i più razionali, come dimostrano una famosa composizione di Nicolò Paganini (1782-1840) intitolata « Moto Perpetuo in sol maggiore, Op. 11, per violino e pianoforte o orchestra »:

e una celebre litografia di Maurits C. Escher (1898-1972), realizzata nel 1961:

La formulazione del Primo Principio della Termodinamica come noi lo conosciamo mise definitivamente in soffitta i sogni di produrre energia gratis. Infatti, estraendo ad esempio lo stantuffo da un cilindro a pareti adiabatiche, ci si accorge che il gas in esso contenuto si raffredda, perchè il lavoro è stato compiuto a spese dell'energia interna del gas. Per trasformazioni adiabatiche si ha Q = 0, per cui W = – ΔU. Se si compie lavoro, l'energia interna diminuisce; e, siccome la temperatura è un indice dell'energia (interna) posseduta dal corpo, la sua temperatura viene a diminuire. Ma sotto lo zero assoluto non si può scendere, e quindi la temperatura non può scendere a oltranza, né a oltranza si può ottenere lavoro senza consumo di energia.
Se ne deduce anche che la trasformazione isoterma, che avviene a U costante (ΔU = 0) è, come anticipato, la più difficile da realizzare, perché per farla avvenire deve essere Q = W. In altre parole, ogni volta che fornisco calore devo muovere il pistone abbastanza da compensarlo sottraendogli un'identica quantità di lavoro meccanico. Insomma, l'isoterma è quasi impossibile da realizzare: anziché restare costante, la temperatura oscilla intorno a un valore medio. Vedremo che l'unica isoterma realizzabile in pratica è quella che avviene in transizione di fase.
Bisogna dire però che il moto perpetuo ora descritto non è l'unico possibile. Si consideri infatti una nave che è in grado di estrarre dal mare in cui naviga il calore che esso riceve dal sole, e di trasformarlo integralmente in lavoro meccanico dell'elica. Questo calore viene restituito al mare per attrito, e così l'energia si conserva e il Primo Principio è rispettato; eppure, la nave continua a procedere all'infinito senza consumare carburante. Com'è possibile? Un simile moto perpetuo non crea lavoro dal nulla, ma semplicemente trasforma integralmente il calore in lavoro e poi il lavoro nuovamente in calore. Il moto perpetuo che crea lavoro dal nulla (con rendimento maggiore del 100 %) viene chiamato moto perpetuo di prima specie, per distinguerlo dal secondo tipo, che trasforma integralmente il calore in lavoro meccanico e viceversa (con rendimento esattamente pari al 100 %), detto moto perpetuo di seconda specie. Il moto perpetuo di prima specie è proibito dal Primo Principio della Termodinamica; vedremo che anche quello di seconda specie è proibito, ma dal Secondo Principio della Termodinamica.
Infine, un'importante considerazione, La convinzione che il moto perpetuo di prima specie sia impossibile è una conseguenza della nostra "fede" nel Primo Principio della Termodinamica. In realtà, nonostante la "consolazione" che deriva dal fatto di possedere uno strumento tanto potente come il principio di conservazione dell'energia, dobbiamo necessariamente ricordare che l'unica certezza nello studio della fisica è quella di non aver mai in possesso una verità assoluta, ma di procedere passo dopo passo verso stadi sempre più elevati di conoscenza, che superano quelli precedenti, così come avvenne quando la Relatività e la Meccanica Quantistica superarono la Fisica Galileiana. Finora però nessun fenomeno, neppure nel campo dell'infinitamente piccolo o dell'infinitamente grande, ha mai violato la (4.6), per cui fino a prova contraria possiamo continuare a ritenere vero quanto scritto in questo paragrafo, e ad affermare che tutti quanti continuano a brevettare progetti di macchine a moto perpetuo sono degli ignoranti in fisica o degli emeriti imbroglioni.

Julius Robert von Mayer (1814-1878)
.
4.5 Interpretazione cinetica del Primo Principio
Mostriamo ora come il Primo Principio possa essere dedotto anche dalle equazioni di conservazione dell'energia, già note dalla Meccanica, a patto di abbandonare il modo di procedere della Termodinamica, cioè la visione macroscopica, e di addentrarsi piuttosto in alcune considerazioni di ordine microscopico.
Consideriamo dunque il sistema termodinamico come un insieme di N particelle microscopiche, interagenti tra di loro e con l'ambiente esterno. Supponiamo che i moti del sistema avvertibili a livello microscopico siano tali da poter trascurare le variazioni di energia cinetica ad essi associate, e che lo siano pure le variazioni dell'energia potenziale dovute a forze di volume (ad esempio la forza gravitazionale). A livello microscopico si verificano dei movimenti disordinati delle particelle del sistema, non avvertibili a livello macroscopico, proprio perchè non coordinati, e quindi disordinati e casuali. Sotto queste ipotesi, il sistema possiede un'energia cinetica non nulla, anche se essa non si manifesta a livello macroscopico. Applico allora alle N particelle (un numero paragonabile al Numero di Avogadro) il Teorema dell'Energia Cinetica:
ΔEc = Σ W (4.7)
che può essere così riscritta:

dove ΔEc è la variazione di energia cinetica di tutto il sistema, Fi è la forza totale agente sull'i-esima particella e Δsi è il suo spostamento infinitesimo. Ora, la forza totale è la somma di due contributi, quello delle forze esercitate da altre particelle del sistema sull'i-esima, che diremo Fint (int sta per "interne"), e quello delle forze esercitate da corpi esterni al sistema, che diremo Fext:
![]()
da cui:
Assumendo che tutte le forze interne siano conservative, cioè che non ci siano attriti interni, si può introdurre per esse un'energia potenziale Uint tale che:
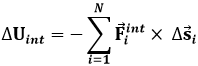
La diventa allora:
Ora, la somma ΔEc + ΔUint è l'energia meccanica totale del sistema, in quiete macroscopica ma non microscopica. Può essere identificata con l'energia interna U del sistema. Quanto al secondo membro, esso non coincide con il lavoro esterno termodinamico, perchè questo è associato solo a spostamenti macroscopici della frontiera. Ora, affinché ciò avvenga bisogna che un gran numero di particelle si muovano in modo coordinato nella stessa direzione presso la frontiera; moti isolati e caotici delle particelle non sono avvertibili a livello macroscopico. Per questo, il vettore Δs deve essere scomposto in una componente "ordinata" Δsord ed in una "caotica" Δscaot. Si ha così:
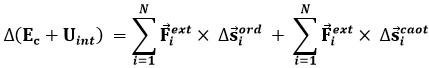
Chiaramente, il termine:

rappresenta il lavoro esterno termodinamico, a parte ovviamente il segno, perchè noi abbiamo considerato positivo solo quello esercitato dal sistema sull'ambiente, mentre questo è quello che l'ambiente (Fext) esercita sul sistema. Per riottenere il Primo Principio, cioè la (4.6), basta identificare:
E si ha così ΔU = Q – W. La (4.10) ci permette di arrivare ad una scoperta di fondamentale importanza: il calore è l'effetto del moto disordinato delle molecole che costituiscono i corpi. Siccome tale moto è privo di una direzione preferenziale, a differenza di quello che produce il lavoro meccanico, è evidente che non è avvertibile a livello macroscopico, ma si manifesta come calore. Si parla perciò di agitazione termica delle molecole. Più oltre vedremo anche un'interpretazione meccanica della temperatura, e sarà facile vedere come essa è un perfetto accordo con questa del calore.
Ci sono buone ragioni per credere che, a dispetto, di quanto la nostra vista limitata ci vuole far credere, tutta la natura sia animata da un moto continuo delle sue molecole. È abbastanza intuitivo fin da ora capire che, più si alza la temperatura, più tale moto diventa violento, mentre, viceversa, si affievolisce andando verso le basse temperature. Allo zero assoluto le molecole risultano ferme; e questo è uno dei motivi per cui tale temperatura è la minima pensabile. Non si può immaginare, infatti, delle molecole meno che ferme!
.
4.6 Determinazione dell'energia interna
Per ogni sistema termodinamico, compiutamente caratterizzato da due variabili X ed Y, esiste sempre un legame che permette di conoscere il valore dell'energia interna U, assegnati i valori di X e di Y nello stato da noi considerato. Nel caso dei gas rarefatti, questo legame è molto semplice. Descriviamo dunque l'esperienza con cui James Prescott Joule giunse al calcolo di tale valore. Tale esperienza prende il nome di espansione senza lavoro esterno o espansione libera di Joule.

Sia dunque il dispositivo visibile qui sopra: un calorimetro a pareti adiabatiche, nel quale sono contenuti due recipienti A e B a pareti rigide, cioè senza stantuffi in grado di fornire lavoro dall'esterno. Essi sono separati da una valvola; nel primo è presente un gas alla pressione iniziale P, nel secondo invece è praticato il vuoto. Tutto il sistema è in equilibrio termico ad una temperatura T, segnata dal termometro.
Io apro la valvola e lascio espandere bruscamente il gas, fino a che esso non si è espanso in B, raggiungendo una nuova pressione P'. All'equilibrio, mi accorgo che la temperatura è invariata.
Se il gas è abbastanza rarefatto, questo risultato è facilmente verificabile mediante l'esperimento. Discutiamolo alla luce del Primo Principio. Anzitutto, il lavoro fornito è nullo, poiché le pareti sono rigide; però anche lo scambio di calore è nullo, avendo le pareti adiabatiche. Se ne conclude che anche ΔU = 0.
Eppure, sia la pressione che il volume del gas sono cambiati, perchè il gas si è espanso e la sua pressione è calata. Si parla di "espansione libera" del gas, perchè esso non incontra resistenze nell'aumentare il proprio volume; si tratta chiaramente di un'operazione irreversibile, perchè il gas non tornerà mai da solo nel recipiente A, come discuteremo nel capitolo 7. Siccome l'unica variabile che è rimasta costante è la temperatura, mentre U resta costante, si può dedurre che, nel corso di un'espansione libera del gas, l'energia interna è funzione della sola temperatura:
U = U(T) (4.11)
Naturalmente, questo vale solo se il gas è abbastanza caldo e rarefatto, cioè se è un gas perfetto. Sì, ma come determinare la funzione (4.11) che lega U a T? Prendiamo in considerazione, allo scopo, una trasformazione comoda, per esempio un'isocora reversibile. Per essa già sappiamo che W = 0, quindi ΔU = Q. Ricordiamo la definizione di calore specifico a volume costante:
![]()
Da essa si ricava:
ΔU = n cV ΔT
Come si vede, a tale semplice espressione siamo giunti attraverso il calcolo in termini finiti. In termini differenziali, con gli strumenti dell'Analisi Matematica, la precedente andrebbe così scritta:
dU = n cV dT (4.12)
e integrando:
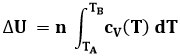
Come si vede in questo grafico, nel caso dell'acqua cV(T) è variabile con la temperatura. Per i gas rarefatti, tuttavia, si verifica sperimentalmente che il calore specifico è quasi costante. In particolare, per i gas monoatomici (come l'elio) si ha cV = 3 R / 2, dove R è la costante dei gas perfetti, mentre per i gas biatomici (ad es. l'idrogeno) si ha cV = 5 R / 2, anche se l'approssimazione è meno buona che nel caso dei gas monoatomici: una spiegazione di questi valori la daremo nel § 9.4. Sostituendo questi valori costanti nella (4.12), cV esce dall'integrale e si ha:
U = U0 + n cV dT (4.13)
U0 giustifica il fatto che non si conoscono i valori assoluti di energia interna, ma solo le sue variazioni. Se poniamo U = 0 per T = 0, si ottiene semplicemente U = n cV T.
Questo risultato vale naturalmente solo per i gas perfetti; per quelli reali, U = U ( P , V , T ). L'utilità del fatto di prendere in considerazione il gas perfetto, anche se è solo un'astrazione fisico-matematica, risiede nella possibilità di usare equazioni semplici come la (4.13), tat'è vero che, grazie ad esse, un gas perfetto si può definire anche come il gas che soddisfa all'equazione di stato del tipo P V = n R T, e la cui energia interna è data da U = n cV T. Ciò ci sarà utile per comprendere in termini microscopici anche le variabili che finora abbiamo definito solo in maniera operativa.
Esempio 4.1: Tre moli di gas perfetto dallo stato iniziale a VA = 80 l e a PA = 1 atm allo stato finale a VB = 60 l e PB = 2 atm, mediante la trasformazione rappresentata in figura, rappresentata da un segmento nel Piano di Clapeyron:

Il gas è biatomico. Quanto calore scambia il gas con l'ambiente?
Naturalmente basta usare il Primo Principio della Termodinamica: Q = ΔU + W. Il ΔU si calcola facilmente usando la (4.13):
Occorre però conoscere la differenza di temperatura. Ovviamente useremo la (3.3), trovando:
TA = PA VA / n R = 1 atm x 80 l / 3 mol x 0,0821 l atm / K mol = 324,8 K
TB = PB VB / n R = 2 atm x 60 l / 3 mol x 0,0821 l atm / K mol = 487,2 K
E quindi ΔT = + 162,4 K. La (4.14) ci dice che:
ΔUAB = 3 mol x 8,31 J/K mol x 2,5 x 162,4 K = 10121,6 J
Bisogna poi calcolare il lavoro: per questo, basta ricordare che l'area AA'B'B sottesa dal grafico della trasformazione nel piano di Clapeyron è rappresentata dal lavoro da essa compiuto. Ma l'area sottesa dalla nostra trasformazione è un trapezio, ed è facile calcolarne l'area. L'area di un trapezio la si ottiene moltiplicando la somma delle basi per l'altezza e dividere il risultato per due; la base maggiore è PB = 2 atm = 2,026 x 105 Pa, la base minore è PA = 1 atm = 1,013 x 105 Pa, mentre l'altezza è VB – VA = – 20 l = – 0,02 m3: non c'è da stupirsi che sia negativa, visto che lo è la sua altezza! Se ne conclude che il lavoro cercato è:
WAB = ( 2,026 x 105 + 1,013 x 105 Pa ) x ( – 0,02 m3 ) / 2 = – 3039 J
Il lavoro perciò è compiuto dal sistema sull'ambiente. Se ne conclude che QAB = ΔUAB + WAB = 7082,6 J. Il calore è positivo, dunque è assorbito.
Esempio 4.2: Tre moli di gas perfetto passano dallo stato iniziale a TA = 27°C e a PA = 1 atm allo stato finale a PB = 2 atm, mediante la trasformazione di equazione:
P V2 = cost.
Il gas è biatomico. Quanto calore scambia il gas con l'ambiente?
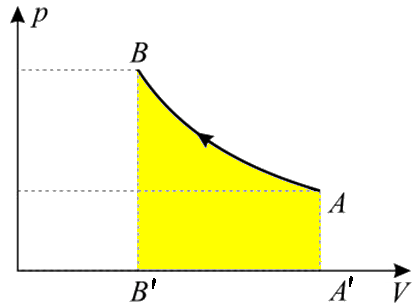
Naturalmente basta usare il procedimento dell'Esempio 4.1. Il ΔU si calcola facilmente usando la (4.14), ma anche in questo caso occorre determinare la differenza di temperatura. L'equazione della trasformazione ci dice che:
PA VA2 = PB VB2
Ma P V = n R T. Sostituendo nella precedente si ha:
n R TA VA = n R TB VB
Semplificando n R, si ha TA VA = TB VB: volume e temperatura sono inversamente proporzionali. Se ne ricava anche:
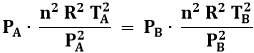
da cui:

e quindi:
ΔU = 3 mol x 8,31 J/K mol x 2,5 x ( 424,26 – 300 ) K = 7750 J
Bisogna poi calcolare il lavoro, cioè l'area AA'B'B: per questo, è indispensabile utilizzare il calcolo integrale., dato che l'area colorata in giallo nella figura non può essere calcolata per via elementare. Da P V2 = PB VB2 segue:
![]()
Per cui:
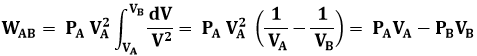
E quindi WAB = n R TA – n R TB = n R ( TA – TB ) = 3 mol x 8,314 J/mol K x ( 300 – 424,26 ) = – 3100 J < 0
Il lavoro perciò è compiuto dall'ambiente sul sistema. Se ne conclude che QAB = ΔUAB + WAB = 4650 J. Anche in questo casso il lavoro è assorbito dal sistema.
.
4.7 La Relazione di Mayer e la trasformazione adiabatica
Abbiamo visto che, oltre che dalle relazioni P V = n R T ed U = n cV T, il gas perfetto è caratterizzato dalla proprietà per cui cV = 3 R / 2 per un gas monoatomico e 5 R / 2 per un gas biatomico. E cP? Lo si può calcolare in modo semplice? Sì, grazie alla cosiddetta Relazione di Mayer, che si può ricavare direttamente dal Primo Principio della Termodinamica. Nel § 1.6 si è visto che:
![]()
Sostituendo in essa la (4.6) si ricava:
![]()
A pressione costante, inoltre, si ha che W = P ΔV. Ne consegue che:
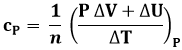
Sempre a pressione costante, P ΔV = n R ΔT, mentre ΔU = n cV ΔT. Se ne conclude:
![]()
Quindi, per un gas perfetto, cP e cV differiscono sempre di R:
cP = cV + R (4.15)
Se il gas è monoatomico, cP = 5 R / 2; se è biatomico, invece, cP è circa pari a 7 R / 2.
Ora, utilizzando la Relazione di Mayer, determineremo l'equazione della trasformazione adiabatica, quella con Q = 0. Avverto però fin da ora che si potrà fare solo con gli strumenti dell'Analisi Matematica; chi non dispone di essi, passi direttamente al risultato. Differenziando entrambi i membri dell'equazione P V = n R T, si ottiene:
P dV + V dP = n R dT
Ricaviamo da essa dT:
![]()
E siccome dU = n cV dT, ne segue:
![]()
Ma, se Q = 0, dU = – d*W = – p dV. Se ne ricava:
![]()
Questa è un'equazione differenziale. Riscriviamola in questa forma:
![]()
Semplifichiamo la R a denominatore e usiamo la Relazione di Mayer:
![]()
Usiamo la separazione delle variabili:
![]()
Ora integriamo ambi i membri tra A e B, e otteniamo:
![]()
Questa si può riscrivere:
Cambiamo nome alla costante e definiamo:
![]()
Def. 4.4: Si indica con γ il rapporto tra i calori specifici a pressione e a volume costante di un gas perfetto, detto coefficiente di dilatazione adiabatica.
Per il gas monoatomico:
![]()
Invece, per il gas biatomico si ha circa:
![]()
La (4.16) allora può essere riscritta:
Questa è l'equazione della trasformazione adiabatica. Anch'essa è una politropica, quando si pone k = γ. Possiamo dunque trovare il lavoro compiuto lungo tale trasformazione, usando la formula (4.4):
![]()
Adoperando l'equazione P V = n R T, è possibile riscrivere la (4.17) in termini di temperatura e volume, oppure di temperatura e pressione:
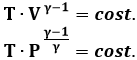
Rappresentando la (4.17) nel piano di Clapeyron, si ottiene una curva che ricorda l'isoterma, ma che è più ripida di quest'ultima, come si vede nel grafico sottostante, perchè γ è sicuramente maggiore di 1, essendo cP > cV per via della Relazione di Mayer. Di questo dovremo tenere conto, quanto disegneremo i cicli termodinamici, a partire dal ciclo di Carnot.

Vale la pena di raccogliere in una tabella le principali caratteristiche delle trasformazioni politropiche:
| TRASFORMAZIONE | k |
equazione |
ΔU | Q | W |
| ISOBARA | 0 |
P = cost. |
n cV ΔT |
n cP ΔT |
P ΔV |
| ISOTERMA | 1 |
P V = cost. |
0 |
|
|
| ADIABATICA | γ |
P Vγ = cost. |
n cV ΔT | 0 |
– n cV ΔT |
| ISOCORA | ∞ |
V = cost. |
n cV ΔT | n cV ΔT | 0 |
.
4.8 Il calore specifico delle politropiche
Determiniamo ora, sempre sulla scorta del Primo Principio della Termodinamica, il calore specifico della trasformazione politropica generica, che indicheremo con la lettera Λ (lambda maiuscola). Naturalmente, sarà indispensabile ricorrere agli strumenti dell'Analisi Matematica; chi non dispone di essi, salti direttamente al risultato. Per definizione di calore specifico, avremo:
Naturalmente noi prendiamo in considerazione un gas perfetto ed una trasformazione reversibile. Allora, per il Primo Principio:
d*Q = dU + d*W = n cV dT + P dV
L'equazione della politropica è P Vk = C, dove C indica una costante, da cui si ottiene:
![]()
Dobbiamo ricavare V in funzione di T, usando l'equazione dei gas perfetti:
![]()
Se ne ricava:
![]()
E quindi:
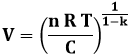
Ora dobbiamo differenziare entrambi i membri, il secondo rispetto a T. Si ha così:

Dato che P = C / Vk, si ottiene:
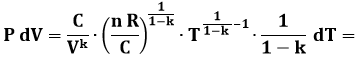

Se ne ricava:
![]()
Sostituendo nella (4.18) avremo:

In conclusione:
Vediamo alcuni ben noti casi particolari:
1) se k = 0 (isobara) si ha cΛ = cV + R = cP per la relazione di Mayer.
2) se k → ∞ (isocora) si ha cΛ = cV + 0 = cV, com'è giusto che sia.
3) se k = 1 (isoterma) si ha cΛ → ∞; infatti non ha senso parlare di calore specifico se la temperatura è costante, perchè la temperatura non varia qualunque sia l'apporto di calore.
4) Se k = γ (adiabatica) si ha:

Ma cV – cP = – R , e quindi cΛ = cV – cV = 0. Infatti non c'è scambio di calore, per cui d*Q = 0 e cΛ = 0.
Esempio 4.3: Si consideri la trasformazione P V2 = cost. dell'Esempio 4.2. Si tratta di una politropica con k = 2, e il gas preso in considerazione è biatomico, dunque:
![]()
Perciò:
![]()
come si era già trovato. Il calcolo da noi eseguito era dunque corretto, e abbiamo trovato una strada alternativa per determinare il calore scambiato nel corso di una trasformazione politropica.

Heike Kamerlingh Onnes (1853-1926)
.
4.9 L'entalpia e la Legge di Hess
Torniamo ora al caso dell'isobara. Si è visto che, lungo di essa, WAB = P ΔV. Ma allora:
QAB = ΔU + WAB = ΔU + P ΔV = UB – UA + P ( VB – VA ) = ( UB + P VB ) – ( UA – P VA )
Viene allora la tentazione di introdurre una nuova grandezza, pari alla somma tra l'energia interna U e il prodotto della pressione P per il volume V:
H = U + P V
Questa grandezza è nota come entalpia, dal greco "enthalpos" ("bruciare all'interno"), e fu introdotta per la prima volta nel 1875 da Josiah Willard Gibbs (1839-1903), del quale sentiremo riparlare; egli la chiamò semplicemente « calore a pressione costante », mentre il termine entalpia, coniata sul modello di "energia", apparve per la prima volta nella letteratura scientifica nel 1909, in una pubblicazione di Heike Kamerlingh Onnes (1853-1926), fisico olandese che eseguì fondamentali ricerche sulle temperature prossime allo zero assoluto, scoprendo tra l'altro la superconduttività. Il simbolo "H" per indicare l'entalpia fu invece introdotto per la prima volta nel 1922 da Alfred W. Porter (1863-1939).
Per la trasformazione isobara, l'entalpia è una grandezza di stato, poiché il calore dipende solo dai valori iniziali e dai valori finali di U, P e V. Potremo dunque affermare che:
QP = HB – HA = ΔH
Cioè il calore lungo una trasformazione isobara è pari alla variazione di entalpia.
Questa funzione di stato è importantissima; infatti, le reazioni chimiche avvengono quasi sempre a pressione costante. Siano A e B i reagenti, C e D i prodotti di una reazione chimica. Se essa è endotermica, cioè se assorbe calore, scriveremo:
energia + A + B → C + D
Se vogliamo calcolare quanto vale questa energia, possiamo eseguire un bilancio di entalpia. Se ΔHf è l'entalpia di formazione dei reagenti e dei composti, allora vale la legge di Hess:
Q = ΔHf (C) + ΔHf (D) – ΔHf (A) – ΔHf (B)
Tale legge fu formulata per la prima volta nel 1840 dal chimico svizzero Germain Henri Hess (1802-1850), ed è usatissima in chimica. Le entalpie di formazione sono tabulate sui manuali; le sostanze elementari, come le molecole di H2, O2, eccetera, hanno entalpia di formazione nulla.
Esempio 4.4: Si consideri la reazione:
CO + H2O → CO2 + H2
che avviene a circa 500°C. Sa che:
ΔHf
(CO) = – 110,54 KJ mol–1
ΔHf (H2O) = – 241,84 KJ mol–1
ΔHf (CO2) = – 393,50 KJ mol–1
Sono negativi perchè sono calori ceduti dal sistema. Allora, per la legge di Hess:
ΔH = ΔH (prodotti) – ΔH (reagenti) = ΔHf (CO2) – ΔHf (H2O) – ΔHf (CO) = – 41,12 KJ mol–1
Siccome il risultato è negativo, la reazione è esotermica (l'energia dei reagenti è minore di quella dei prodotti, perchè vi è liberazione di energia).
Germain Henri Hess (1802-1850)
Se nella reazione interviene l'ossigeno, si parla di combustione. La legge di Hess permette allora di ricavare il calore di combustione.
Esempio 4.5: Sia la combustione dell'ossido di carbonio:
2 CO + O2 → 2 CO2
Poiché O2 è una specie elementare, ha ΔH di formazione nullo. Ne segue, con i dati scritti sopra:
Qcombustione = ΔHf (CO2) – ΔHf (CO) = – 282,96 KJ mol–1
Anche la combustione è evidentemente esotermica. Osserviamo che, aggiungendo 2 H2 a destra e a sinistra della relazione precedente, 2 H2 e O2 reagiscono a formare acqua, e si ritrova la reazione dell'Esempio 4.4. Però anche la reazione 2 H2 + O2 → 2 H2O è una reazione di combustione (dell'idrogeno); si ha:
Qcomb (H2) = ΔHf (H2O) = – 241,84 KJ mol–1
E quindi, per la reazione dell'Esempio 4.4:
ΔH = Qcomb (CO) – Qcomb (H2) = – 41,12 KJ mol–1
che è ovviamente lo stesso risultato di prima.
.
E con questo, abbiamo detto tutto circa il Primo Principio della Termodinamica. È ora di parlare del Secondo Principio, e lo faremo nel capitolo successivo. Per tornare all'indice, invece, cliccate qui.
![]()