![]()
|
"Dall'acqua Allah ha creato tutti gli animali. Alcuni di loro strisciano sul ventre, altri camminano su due piedi e altri su quattro." Corano, Sura XXIV, 45 |
.
6.1 La degradazione dell'energia
In questo capitolo affronteremo il problema, brillantemente risolto da Clausius, di definire una grandezza di stato che valuti il grado di irreversibilità di una trasformazione energetica. Già ai tempi di Carnot era chiaro che, da un punto di vista tecnologico, i processi reversibili risultano più vantaggiosi di quelli irreversibili. I primi però rappresentano solo il limite a cui dovrebbero tendere questi ultimi, per realizzare le condizioni migliori, cioè quelle di perfetta reversibilità, in quanto è praticamente impossibile ridurre a zero tutti gli attriti interni del ciclo. Lo stesso Ciclo di Carnot di cui abbiamo parlato nel § 5.3 rappresenta un livello di rendimento irraggiungibile, poichè:
a) le trasformazioni che lo
compongono sono reversibili;
b) le trasformazioni perfettamente isoterme e perfettamente adiabatiche sono
irrealizzabili tecnicamente;
c) le sorgenti si trovano a temperatura costante, mentre per assorbire calore da
un corpo è necessario che vi sia una differenza di temperatura tra noi ed esso.
Quindi, tutti i rendimenti delle macchine reali sono inferiori ad ηc, e perciò i rendimenti di Secondo Principio sono tutti inferiori ad uno. Mentre il rendimento di Primo Principio η = W/Q1 misura l'abilità con cui una macchina converte il calore in lavoro meccanico, il rendimento di Secondo Principio misura l'abilità con cui una macchina annulla le irreversibilità interne. In questo senso il Ciclo di Carnot rappresenta il meglio che c'è nell'universo, ma è un ciclo ideale, che può avvenire solo su tempi praticamente infiniti, essendo le trasformazioni quasi-statiche.
Si può supporre che, nei processi reversibili, a parità di calore disponibile, l'energia perduta sia minima e il lavoro ottenuto massimo; tuttavia, bisogna tenere conto del fatto che il calore non ha sempre lo stesso "valore energetico": esso dipende dalla temperatura a cui il calore si trova. Per esempio, 1000 J a 500°C non hanno lo stesso valore di 1000 J a 50°C, o a 5°C. Per rendercene conto, prendiamo proprio 1000 J a 500°C e facciamoli assorbire da un gas perfetto, che poi ne cede una parte a una sorgente a 0°C attraverso un Ciclo di Carnot. Siccome le due temperature corrispondono rispettivamente a 773,15 K e 273,15 K, come si è visto nel § 5.3 il rendimento di tale ciclo è pari a:
![]()
e quindi il lavoro ottenibile da tale ciclo è W = ηc x Q1 = 0,647 x 1000 J = 647 J. Se invece la sorgente calda si trova a 50°C e la sorgente fredda è sempre la stessa, stavolta le temperature estreme sono 323,15 K e 273,15 K, e quindi il rendimento del ciclo scende a:
![]()
e quindi il lavoro ottenibile da tale ciclo è W = ηc x Q1 = 0,155 x 1000 J = 155 J. Se infine la sorgente calda si trova ad appena 5°C, stavolta le temperature estreme sono 278,15 K e 273,15 K, e il rendimento del ciclo è appena pari a:
![]()
e quindi il lavoro ottenibile da tale ciclo è solamente pari a W = ηc x Q1 = 0,018 x 1000 J = 18 J. Più è bassa la temperatura della sorgente calda, minore è il rendimento, e minore è il lavoro meccanico che posso tirarne fuori, perchè è più facile trasformare in lavoro il calore quando esso si trova ad alta temperatura.
Da queste considerazioni discende che, in luogo del calore Q da cui può unicamente dipendere il lavoro utile ottenibile, né il lavoro perduto nel ciclo rispetto a un processo reversibile, conviene adoperare una combinazione di Q e di T (la temperatura assoluta a cui si trova il calore Q). Clausius in particolare ebbe l'idea che ogni trasformazione reale di calore in lavoro lasci sempre una "traccia termodinamica" espressa dal rapporto tra Q e T, tanto più marcata quanto più il suo valore si discosta da quello della trasformazione reversibile. In altre parole, ogni trasformazione reale in cui avvengono scambi termici è accompagnata da un certo valore di Q / T, il quale ci dice che qualcosa è cambiato nell'universo dopo la trasformazione.
Fissiamo anzitutto l'attenzione su un Ciclo di Carnot che opera tra le temperature T1 e T2 < T1. Si è visto che:

da cui:
![]()
cioè i calori scambiati in un Ciclo di Carnot sono proporzionali alle temperature assolute alle quali essi sono scambiati. Essa si può così riscrivere:
Introduciamo ora una nuova grandezza di stato, indicata con S e definita come il rapporto tra il calore scambiato e la temperatura a cui esso viene scambiato; perciò S = Q / T, e si misura in J/K o J K–1. Si tratta di una grandezza estensiva e, perciò, additiva. Questa grandezza di stato venne introdotta per la prima volta da Rudolf Clausius nel suo "Abhandlungen über die mechanische Wärmetheorie" ("Trattato sulla teoria meccanica del calore"), pubblicato nel 1864. Egli la chiamò inizialmente Verwandlung, cioè "Trasformazione", ma in seguito cambiò idea e coniò il termine entropia, oggi universalmente utilizzato. Tale parola deriva dal greco "en", "dentro", e "tropé", "rivolgimento", sul modello di energia: Clausius intendeva riferirsi al legame tra il movimento delle molecole interne al sistema e l'energia interna o il calore. La (6.1) ci porta allora a scrivere:
![]()
Il Ciclo di Carnot è un ciclo reversibile, per cui è lecito scrivere ΔSrev = 0. Noi sappiamo che il rendimento di tutti i cicli reali è minore di quello di Carnot; ne consegue che:

Da qui si ricava:
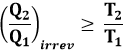
La si può riscrivere:
cioè:
![]()
Ne consegue un risultato importantissimo: l'entropia di un sistema resta costante in seguito ad una trasformazione reversibile, aumenta in seguito ad una irreversibile. La conservazione dell'entropia vale solo per le trasformazioni reversibili; viceversa, si possono definire processi reversibili quelli che avvengono ad entropia costante, cioè le isoentropiche. Ne consegue che l'entropia è una grandezza di stato che misura l'irreversibilità del sistema.
Approfondiamo la questione analizzando un caso particolare di trasformazione irreversibile: il passaggio di calore tra due corpi a diversa temperatura. Siano dunque A e B due corpi rispettivamente alle temperature T2 e T1 > T2, ed aventi capacità termiche molto elevate, in modo che le loro temperature non subiscano variazioni apprezzabili anche in seguito a grandi scambi energetici. Ponendo i due corpi a contatto diretto tra di loro, una quantità di calore ΔQ viene spontaneamente trasferita da A a B; ΔQ è negativa per A che la cede e positiva per B che la acquista. Ne consegue che la variazione di entropia di A è – ΔQ / T1, mentre quella di B è pari a + ΔQ / T2. La variazione totale di entropia del sistema formato dai due corpi in seguito all'avvenuto scambio di calore è perciò pari a:
Essendo T1 > T2, ne consegue che 1 / T1 < 1 / T2, per cui ΔS > 0. Anche in questo caso, a seguito dello scambio di calore in modo irreversibile, l'entropia è aumentata.
Esempio 6.1: Una quantità di calore pari a 100.000 J passa spontaneamente da un corpo a 400 K a un altro corpo a 250 K. Qual è la variazione di entropia del sistema?
Applicando la (6.3) avremo:
![]()
Si noti che, se il calore fluisse dal corpo a 250 K a quello a 400 K, il primo termine sarebbe negativo e il secondo positivo, per cui la variazione di entropia sarebbe paria a ΔS = – 150 J / K. Per il Secondo Principio della Termodinamica, Enunciato di Clausius, questo passaggio di calore non potrà mai avvenire spontaneamente, e quindi l'entropia non potrà mai diminuire spontaneamente, ma solo restare costante (nelle trasformazioni reversibili) o aumentare (in quelle irreversibili! Ne segue il:
SECONDO PRINCIPIO DELLA TERMODINAMICA, ENUNCIATO DELL'ENTROPIA: È tecnicamente e teoricamente impossibile realizzare una trasformazione termodinamica il cui unico risultato è quello di abbassare l'entropia di un sistema.
Sulla base di questo nuovo enunciato, è possibile sintetizzare sia il Primo che il Secondo Principio della Termodinamica in un modo elegante e suggestivo: l'energia dell'universo è costante, mentre la sua entropia è in aumento! L'entropia potrebbe al massimo restare costante se si seguissero solo trasformazioni reversibili, ma gli attriti interni ad ogni sistema vanificano questa possibilità.
Esempio 6.2: Un chilogrammo di ghiaccio si scioglie interamente, trasformandosi in acqua liquida a pressione ambiente. Di quanto varia la sua entropia?
In questo caso il calore è quello latente necessario per la fusione del ghiaccio, e durante la trasformazione (un passaggio di stato) la temperatura resta costante. Nel § 2.2 si è visto che per fondere 1 kg di ghiaccio alla temperatura di 0°C = 273,15 K occorrono 333.500 J, e quindi:
![]()
Anche in tal caso il ghiaccio assorbe il calore, che risulta positivo, e quindi ΔS > 0. Ancora una volta, l'entropia aumenta se il processo è irreversibile, come la fusione del ghiaccio. L'entropia è proprio una misura dell'irreversibilità di un sistema termodinamico.
Esempio 6.3: Calcoliamo la variazione di entropia di un sasso di massa m = 2 kg che cade in un laghetto dall'altezza di 10 m, sapendo che la temperatura del laghetto è di 17°C. Calcoliamo anche la variazione di entropia del laghetto.
Il lago contiene molta acqua, per cui la sua temperatura risulta costante. La variazione di entropia del sasso è allora nulla, perchè lo stato iniziale è uguale a quello finale. Quanto invece al laghetto, siccome T è costante, allora ΔU = 0, e la quantità di calore che esso riceve è pari al lavoro meccanico compiuto dal sasso (per il Primo Principio della Termodinamica, Q – W = 0). Ne segue che:

.
6.2 L'integrale di Clausius
In questo paragrafo vedremo come si arriva al concetto di entropia usando gli strumenti dell'Analisi Matematica; chi non è in grado di adoperarli, salti pure direttamente al paragrafo seguente. Generalizziamo anzitutto la (6.1) per un ciclo qualunque. La macchina compie una serie di trasformazioni tutte reversibili, durante il quale il sistema assorbe un calore Q1i e produce un lavoro Wi, con i che varia da 1 a N, funzionando tra due temperature intermedie fra T1 e T2.

Se, come nella figura soprastante, immagino di suddividere il ciclo in un numero grandissimo di Cicli di Carnot di spessore infinitesimo, per ciascuno di essi vale ancora la (6.1), per cui usando il concetto di limite conviene scrivere:
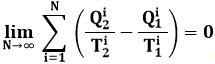
Ma, per N → ∞, Q1i e Q2i sono quantità di calore infinitesime, quindi in Analisi conviene indicarle con il simbolo d*Q, mentre con T indicheremo la temperatura a cui avviene la trasformazione. La somma di infiniti termini infinitesimi prende il nome di integrale, per cui la precedente può essere così riscritta mediante il calcolo integrale:
dove il "rev" scritto vicino al simbolo dell'integrale sta a significare che esso è esteso a tutta la trasformazione ciclica reversibile: i contributi negativi compensano esattamente quelli negativi. La (6.4) prende il nome di integrale di Clausius. Esso conferma l'intuizione da noi avuta che il rapporto Q/T rappresenti una grandezza fisica adatta a valutare la capacità di un sistema di fornire lavoro meccanico, a dispetto delle irreversibilità in esso riscontrabili. Infatti, tutte le volte che il sistema descrive un ciclo formato da trasformazioni tutte reversibili, la variazione dell'integrale di Q/T è nulla, e noi interpretiamo questo fatto dicendo che la potenziale capacità del sistema di produrre lavoro è rimasta immutata. E adesso, compiamo un altro passo avanti.
Dividiamo in due il nostro ciclo reversibile attraverso due punti A e B, e chiamiamo (1) il tratto reversibile superiore (A → B) e (2) il tratto reversibile inferiore (B → A):

Allora la (6.4) fornisce:
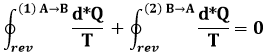
Invertendo tra loro gli estremi di integrazione, l'integrale cambia di segno, per cui la precedente si può riscrivere:

E in definitiva si ha:

Ma allora l'integrale di d*Q / T, calcolato lungo una trasformazione reversibile, dipende dai suoi estremi A e B, ma non dal tipo di trasformazione seguita. Ne consegue che d*Q / T è il differenziale esatto di una funzione di stato, a dispetto del fatto che d*Q non lo è! Tale grandezza di stato è quella che noi abbiamo definito entropia:
![]()
Le sue variazioni sono perciò date dall'integrale di Clausius calcolato tra i due estremi della trasformazione:

Questo integrale fornisce, attraverso grandezze operativamente misurabili, la variazione di entropia lungo una qualsiasi trasformazione aperta, finita e reversibile. Anche l'entropia S, come l'energia interna U, è definita a meno di una costante additiva; i suoi valori dipendono cioè da dove si pone il livello di entropia zero. Come vedremo, a seguito del Terzo Principio della Termodinamica (vedi § 5.6), si pone solitamente nulla l'entropia del sistema allo zero assoluto. Naturalmente, però, ai fini della Termodinamica interessano solo le differenze di entropia tra due stati di equilibrio, quindi la costante è di secondaria importanza.
Ripetiamo ora il ragionamento per una trasformazione irreversibile. Dalla (6.2), scomponendo il ciclo irreversibile in infiniti cicli di Carnot infinitesimi, si ottiene:
Presi ora due stati generici A e B, consideriamo un ciclo formato da una trasformazione irreversibile da A a B e da una reversibile da B ad A. La (6.5) vale anche per questo ciclo, per cui:
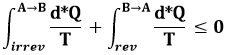
cioè:
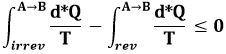
Quest'ultimo integrale coincide con la variazione di entropia da A a B. Ne segue così quella che viene chiamata disuguaglianza di Clausius:
Se il sistema è isolato, esso non scambia calore con l'esterno, per cui d*Q = 0, e si ha:
SB > SA per i processi irreversibili;
SB = SA per i processi reversibili.
La (6.6) si può considerare un ulteriore enunciato del Secondo Principio della Termodinamica, ed è anzi la più semplice formulazione matematica del Secondo Principio: l'integrale di Clausius calcolato lungo una trasformazione reversibile supera quello calcolato lungo ogni trasformazione irreversibile avente gli stessi estremi. La (6.6) si può anche formulare così: la Natura permette che avvengano solo trasformazioni per le quali è soddisfatta la disuguaglianza di Clausius.
La medesima espressione può essere sfruttata per scoprire se una reazione chimica avviene o meno in modo reversibile in quanto, in tal caso, nella (6.6) vale il simbolo di uguale, mentre se avviene in modo irreversibile vale il simbolo di minore.
.
6.3 L'entropia del gas perfetto
Determiniamo ora la variazione di entropia di un gas perfetto. Anche per questo sarà necessario ricorrere al Calcolo Infinitesimale; chi non lo conosce, può passare direttamente al risultato. Anzitutto, per il Primo Principio si ha:
d*Q = dU + d*W
tuttavia dU = n cV dT e d*W = p dV, per cui:
d*Q = n cV dT + P dV
Ora, dalla legge dei gas perfetti (3.3):
![]()
L'ultimo passaggio è stato eseguito ricordando che la derivata di un prodotto di funzioni è data dalla prima per la derivata della seconda, più la derivata della prima per la seconda. Sostituendo nella precedente si ha:
![]()
E quindi, usando la Relazione di Mayer (4.15):
![]()
Utilizzando di nuovo la legge dei gas perfetti P V = n R T, la si può riscrivere:
![]()
Applichiamo ora la (6.6):
![]()
Da qui si ricava:
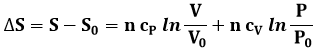
Poiché cP / cV = γ, la si può riscrivere:

E in definitiva:
Abbiamo visto che, per la (4.17), lungo una adiabatica reversibile risulta:
P Vγ = P0 V0γ
E quindi la (6.7) ci dice che:
S = S0 + n cV ln 1 = S0
dunque, lungo un'adiabatica reversibile l'entropia rimane costante. Per questo, una tale trasformazione è detta anche isoentropica.
.
6.4 Il piano di Gibbs
Riprendiamo ora in mano il Ciclo di Carnot che, come si è visto nel § 5.3, è composto proprio da due isoterme e due isoentropiche. È possibile rappresentare tale composizione in modo elegante ed immediato su di un grafico? Certo. Infatti, ricordando la (6.6), si può affermare che, lungo una trasformazione isoterma:
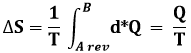
Ne consegue che, lungo una trasformazione isoterma, il calore scambiato può essere trovato con la formula;
QT = T ΔS (6.8)
Si ricordi che, lungo una trasformazione isobara, il lavoro compiuto può invece essere espresso da:
WP = P ΔV
Questo suggeriva di rappresentare le trasformazioni in un piano che ha le pressioni in ordinate e i volumi in ascisse, cioè il Piano di Clapeyron. La (6.8) allora suggerisce di adoperare un nuovo piano, con le temperature assolute in ordinate e l'entropia in ascisse. Tale piano prende il nome di Piano di Gibbs, dal nome dello scienziato americano Josiah Willard Gibbs (1839-1903). Si noti che esso ha in ascisse una grandezza estensiva (l'entropia) e in ordinate una intensiva (la temperatura), esattamente come il Piano di Clapeyron ha in ascisse una grandezza estensiva (il volume) e in ordinate una intensiva (la pressione). Che l'entropia è una grandezza estensiva ce lo dice la (6.7), nella quale è presente il numero di moli, che è una grandezza estensiva come il volume. Due grandezze, una intensiva ed una estensiva, il cui prodotto ha le dimensioni di un'energia, si dicono coniugate, per cui la pressione P ha come coniugata estensiva V. Ne consegue che l'entropia è la coniugata estensiva della temperatura.
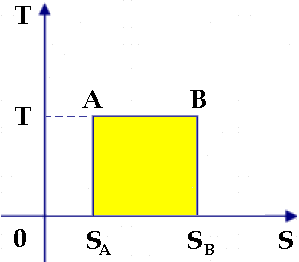
Nel Piano di Gibbs la trasformazione isoterma è rappresentata da una retta orizzontale, per cui il prodotto T ΔS rappresenta l'area sottesa da tale retta. La (6.8), come si è detto, vale solo lungo una trasformazione particolare; ma ogni trasformazione può essere approssimata con una serie di isoterme infinitesime, per cui, quando il numero di tali isoterme diventa grandissimo, l'area sottesa da ogni curva nel piano T-S esprime il calore scambiato lungo tale trasformazione!
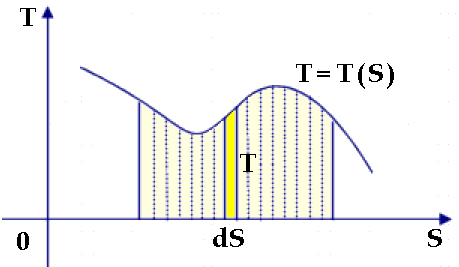
Usando gli strumenti dell'Analisi Matematica, si può scrivere:
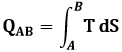
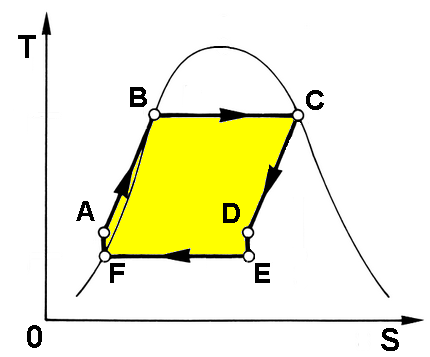
Ora, nel piano di Gibbs le adiabatiche (cioè le isoentropiche) sono rappresentate da rette verticali, per cui il Ciclo di Carnot assume l'incredibile forma di un rettangolo:
È allora facile calcolarne il rendimento. Infatti BC e DA non sottendono alcuna area, perchè sono isoentropiche (ΔS = 0), mentre i calori scambiati lungo le isoterme AB e CD sono pari a:
QAB = TA ( SB – SA ) > 0
QCD = TD (SD – SC ) = – TD ( SB – SA ) < 0
Ed essendo ΔU = 0, per il Primo Principio della Termodinamica si ha:
W = QAB + QCD = ( TA – TD ) ( SB – SA )
Quindi:

Ritroviamo così la prima parte del Teorema di Carnot, per cui ηc dipende dalle sole temperature estreme. Utilizzando l'entropia però è possibile dimostrare agevolmente anche la seconda parte, perchè basta osservare che, fissate due sorgenti di temperature T1 e T2, qualunque ciclo formato da trasformazioni AB e CD che NON sono parallele all'asse delle ascisse (cioè delle entropie) presenta un'area inferiore a quella del rettangolo in cui esso è inscritto:

Idem dicasi se le trasformazioni BC e DA non sono parallele all'asse delle ordinate (cioè delle temperature), perchè in tal caso queste trasformazioni implicano una variazione di entropia ΔS, cioè un calore aggiuntivo che NON è assorbito a temperatura costante, e quindi è minore di quanto sarebbe se la trasformazione fosse verticale come nel Ciclo di Carnot. Conclusione: il ciclo a rendimento massimo è quello a forma di rettangolo nel piano di Gibbs, cioè (lo si è visto) proprio il Ciclo di Carnot.
.
6.5 Le politropiche nel piano di Gibbs
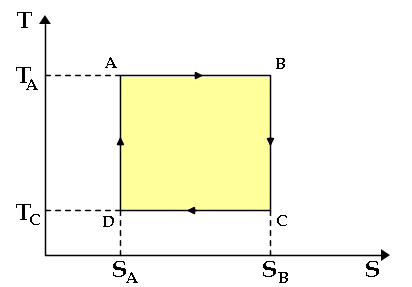
Nel piano di Gibbs, come si è detto, le isoterme sono rappresentate da rette orizzontali e le isoentropiche o adiabatiche da rette verticali. Ma le isobare e le isocore? E le altre politropiche? Consideriamo la (6.7). Se in essa poniamo P = P0 = costante, avremo:

E quindi, lungo un'isobara:
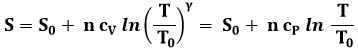
Invertendo la funzione, si trova:
Questa è l'equazione dell'isobara nel piano di Gibbs. Analogamente, ponendo V = V0 = costante nella (6.7), si trova:
![]()
e invertendo:
Questa è l'equazione dell'isocora nel piano di Gibbs. Poiché cV < cP per via della relazione di Mayer (4.15), ci si rende subito conto che nel piano di Gibbs l'isocora ha una pendenza maggiore dell'isobara, come si vede nel grafico sottostante.

Troviamo ora l'equazione generale della politropica (del tipo P Vk = cost.) nel piano di Gibbs. Sostituendo la (4.3) nella (6.7) si ha, con successivi passaggi algebrici:
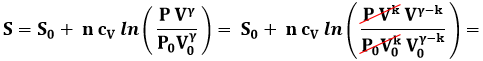
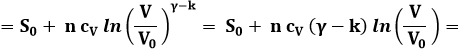
![]()
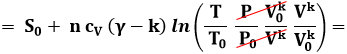
![]()
Ora, uno dei passaggi di questa catena di identità ci dice che:
![]()
E quindi, sostituendo questo risultato nella precedente:

Portiamo ora k ΔS a primo membro:

Invertendo la funzione, troviamo infine:
dove k è il parametro che compare nell'equazione (4.3) della politropica.
Se k = 0, ricordando che γ = cP / cV, la (6.11) si trasforma nella (6.9), che è appunto l'equazione dell'isobara. Se k → ∞, la (6.11) tende alla (6.10), che è l'equazione dell'isocora. Se k = 1, resta solo T = T0, cioè l'isoterma. Se k = γ, dal passaggio precedente la (6.11) si ricava ΔS = 0, cioè l'isoentropica, e quindi l'adiabatica. I conti tornano perfettamente.
Si noti che di solito si pone:
![]()
per cui la (6.11) si riscrive così:
![]()
Se x = γ, si ha k = 0 e quindi l'isobara. Se x = 1, si ha k → ∞, e quindi l'isocora. Se x → ∞, si ha k = 1 e quindi l'isoterma. Se x = 0 si ha k = γ, e quindi l'isoentropica.
Esempio 6.4: È possibile dimezzare contemporaneamente il volume e la pressione di un gas perfetto isolato termicamente dall'ambiente circostante?
Lo scambio di calore è nullo, per cui lo è anche la variazione di entropia (cioè l'integrale di Clausius). Ora, la variazione di entropia dovuta al passaggio dallo stato iniziale ( PA ; VA ) a quello finale ( PA/2 ; VA/2 ) non dipende chiaramente dal percorso seguito. Usiamo allora la (6.7):
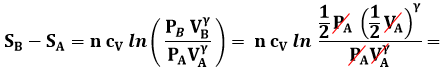
![]()
Si constata subito che tale valore è negativo, per cui la disuguaglianza di Clausius non è soddisfatta, e dunque la trasformazione ipotizzata non è realizzabile spontaneamente, essendo in contraddizione con il Secondo Principio della Termodinamica.

Josiah Willard Gibbs (1839-1903)
Vale la pena di spendere due parole anche per il Piano di Mollier, un piano termodinamico che in ascisse ha l'entropia e in ordinate ha l'entalpia. Esso prende il nome dall'ingegnere austriaco Richard Mollier (1863-1935), che lo introdusse per la prima volta nel 1906. In ingegneria viene usato particolarmente il Diagramma di Mollier (o diagramma psicrometrico) della miscela aria-acqua, che rappresenta l'entalpia di tale miscela in funzione dell'entropia, del volume, della pressione, della temperatura e del titolo di vapore. Tale diagramma viene infatti utilizzato per la progettazione di centrali elettriche, turbine a vapore, compressori e sistemi di refrigerazione. Ecco una versione semplificata del Diagramma di Mollier aria-acqua:
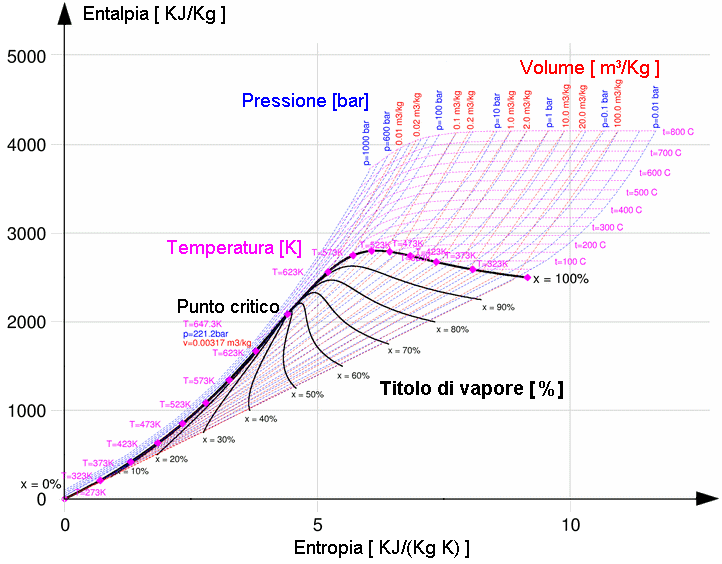
.
6.6 L'energia libera di Gibbs
In base alla disuguaglianza di Clausius, si è visto che:
Qirrev < Qrev
Consideriamo ora una trasformazione a pressione e temperatura costante. Sembra troppo limitante, come condizione? Ebbene, si tenga conto che quasi tutte le reazioni chimiche avvengono a pressione atmosferica e a temperatura ambiente. Ora, si sa che a temperatura costante:
Qrev = T ΔS = T ( S2 – S1 )
e a pressione costante:
W = P ΔV = P ( V2 – V1 )
Allora, essendo:
Qrev > Qirrev = ΔU + W
ne segue che:
T S2 – T S1 > U2 – U1 + P V2 – P V1
Quest'ultima si può riscrivere:
U1 + P V1 – T S1 > U2 + P V2 – T S2
indipendentemente dal tipo di reazione. Di conseguenza posso introdurre una nuova funzione di stato, detta energia libera di Gibbs e indicata con G:
G = U + P V – T S = H – T S
La disuguaglianza di Clausius allora si può così riscrivere in termini di energia libera:
![]()
dove l'uguale vale solo per le trasformazioni reversibili. Ed ecco l'ennesima versione del Secondo Principio della Termodinamica:
la natura lascia avvenire solo le trasformazioni che comportano una diminuzione di energia libera
Come già nel caso dell'entalpia (vedi § 4.9), questo non è solo un artificio matematico. Infatti la variazione di energia libera corrisponde al lavoro utilizzabile, cioè al lavoro che si può trasformare in altre forme di energia: nelle pile, ad esempio, in energia elettrica.
Lutile = – ΔG
Infatti, dovendo aumentare l'entropia complessiva, deve per forza risultare:
ΔStot = ΔSsistema + ΔSambiente > 0
cioè:
![]()
Se il calore è scambiato a pressione costante, come in questo caso, si ha:
ΔH = Qrev
e quindi:
![]()
da cui:
ΔH – T ΔS = ΔG < 0
Presa allora una qualunque reazione chimica del tipo:
α A + β B → γ C + δ D
risulta subito:
ΔG = γ ΔG (C) + δ ΔG (D) – α ΔG (A) – β ΔG (B)
dove ΔG (A) è l'energia libera di formazione della specie chimica A. Osserviamo che, siccome ΔG = ΔH – T ΔS, si ha:
1) se la reazione è endotermica (ΔH > 0) ed ordinante (ΔS < 0), cioè se diminuisce il numero dei legami chimici, ΔG > 0 e la reazione non avviene mai;
2) se la reazione è esotermica (ΔH < 0) e disordinante (ΔS > 0), cioè se aumenta il numero dei legami chimici, ΔG < 0 e la reazione avviene a qualunque temperatura;
3) se la reazione è endotermica (ΔH > 0) e disordinante (ΔS > 0), avviene solo quando T ΔS prevale su ΔH, cioè per alte temperature;
4) se la reazione è esotermica (ΔH < 0) ed ordinante (ΔS < 0), avviene solo quando ΔH prevale su T ΔS, cioè per basse temperature.
Esempio 6.5: Determinare la variazione di energia libera di Gibbs per la combustione completa di una mole di metano, e dire se la reazione è spontanea.
La reazione in questione è CH4 + 2 O2 → CO2 + 2 H2O. La variazione di energia libera cercata è data da:
ΔG = ΔG (CO2) + 2 ΔG (H2O) – ΔG (CH4) – 2 ΔG (O2)
Ora, le energie libere di formazione delle quattro specie chimiche interessate dalla reazione sono:
ΔG (CH4) = – 50,8 KJ/mol
ΔG (CO2) = – 394,4 KJ/mol
ΔG (H2O)
= – 237,0 KJ/mol
Invece ΔG (O2) = 0 KJ/mol perchè le specie chimiche elementari hanno energia libera di formazione nulla. Ne consegue che:
ΔG = – 394,4 KJ/mol + 2 x ( – 237,0 KJ/mol ) – ( – 50,8 KJ/mol ) = – 817,6 KJ/mol
Poiché il valore di ΔG trovato è negativo, ciò significa che la reazione è spontanea, in accordo con la nostra esperienza quotidiana: infatti il metano brucia spontaneamente, avvicinando un cerino acceso al fornello, e costituisce un combustibile assai diffuso. Una mole di metano, cioè 16 g di questo gas, bruciando libera ben 817.600 J.
Aggiungiamo che esiste anche una differente energia libera, la cosiddetta energia libera di Helmholtz, che prende il nome dal medico e fisico tedesco Hermann von Helmholtz (1821-1894), detto dai suoi contemporanei "il Cancelliere della Fisica". Indicata con A, essa è così definita:
A = U – T S = G – P V
Si può dimostrare che nelle trasformazioni isotermocore (in cui T e V sono costanti) l'energia libera di Helmholtz diminuisce per un processo irreversibile, mentre è costante per un processo reversibile. In termini di energia libera di Helmholtz, dunque, la disuguaglianza di Clausius si riscrive così:
![]()

Hermann von Helmholtz (1821-1894)
.
6.7 L'Equazione di Clapeyron e la tensione di vapore
Anche questo paragrafo, per essere compreso appieno, richiede gli strumenti dell'Analisi Matematica, e dunque potrà essere compreso appieno solo da chi può destreggiarsi con essa. Partiamo dalla definizione di energia libera di Gibbs data nel § precedente:
G = U + P V – T S
Differenziamo ora ambi i membri della precedente, usando la regola della differenziazione del prodotto:
dG = dU + d(PV) – d(TS) = dU + P dV + V dP – T dS – S dT
Ma, per il Primo Principio della Termodinamica, se P e T sono costanti (trasformazioni isotermobariche):
dU = d*Q – d*W = T dS – P dV
Allora la precedente fornisce:
dG = T dS – P dV + P dV + V dP – T dS – S dT = V dP – S dT
Se ne ricava così che:
dG = V dP – S dT (6.12)
Supponiamo ora di prendere in considerazione una transizione di fase, per esempio da solido (s) a liquido (l). Esso avviene per l'appunto a pressione e temperatura costanti, ed è reversibile, per cui si può ammettere che risulti:
G (s) = G (l)
e quindi, anche:
dG (s) = dG (l)
cioè, per la (6.12):
V (s) dP – S (s) dT = V (l) dP – S (l) dT
La si può riscrivere:
[ S (l) – S (s) ] dT = [ V (l) – V (s) ] dP
Ma, siccome nelle transizioni di fase la temperatura è costante, si ha:
![]()
Sostituisco nella precedente ed ho:
Questa è chiamata equazione di Clapeyron, e fornisce il legame (differenziale) tra pressione e volume nelle trasformazioni isotermobariche, come per eempio durante i cambiamenti di fase. Si osservi che, se ΔH > 0 e ΔV > 0, cioè se il volume aumenta ed è assorbito calore durante il processo, la pendenza della curva P = P (T) è positiva, altrimenti è negativa. In termini finiti, per chi non conosce il concetto di derivata, la (6.13) si può scrivere:
![]()
L'equazione di Clapeyron è importantissima, perchè può essere usata per esempio per calcolare la tensione di vapore di un gas, da noi introdotta nel § 2.1, cioè la pressione che esercita un vapore in equilibrio con un liquido ad una certa temperatura. Certi autori parlano di "pressione di vapore", anziché di tensione di vapore, perché non si tratta di una forza, ma in questo ipertesto si è deciso di utilizzare il termine imposto dalla consuetudine storica. Conoscere la tensione di vapore è importante, poiché come si è già detto una sostanza bolle solo allorché la sua tensione di vapore, evidentemente funzione della temperatura, uguaglia la pressione atmosferica esterna. Chiedersi qual è la tensione di vapore di una sostanza equivale dunque a chiedersi qual è la sua temperatura di ebollizione. Scriviamo perciò la (6.13) nel caso dell'ebollizione:
![]()
dove ΔHev è, evidentemente, il calore latente di evaporazione, ricavabile sperimentalmente. Ora, consideriamo per un momento ΔHev = V (g) – V (l). A 100°C, una mole di vapor d'acqua ha un volume di 30 litri, dato ricavabile dall'equazione dei gas perfetti o dall'equazione di Van der Waals, mentre una mole d'acqua liquida, pari a 18 grammi, ha un volume di soli 0,018 litri. Il volume del liquido è sempre trascurabile rispetto a quello del vapore. Perciò:
![]()
Allora l'equazione di Clapeyron diventa:
![]()
dove con h si indica l'entalpia molare, cioè il calore necessario per far evaporare una mole di liquido. Se suppongo che il calore latente molare vari poco con la temperatura, posso separare le variabili:
![]()
Integro ambi i membri tra lo stato iniziale e quello finale, ed ho:

cioè:
![]()
da cui ricaviamo:
![]()
I Δhev sono tutti positivi; se aumento la temperatura (T2 > T1), ho 1 / T1 = 1 / T2 e ne segue facilmente che anche la pressione aumenta. Questo è facilmente intuibile anche dal punto di vista qualitativo , poiché all'aumentare della temperatura aumenta l'energia cinetica delle singole molecole, e più molecole si staccano dal liquido, aumentando la pressione di vapore. Come accennato, è questo il principio su cui si basa la pentola di Papin, che dà il titolo a questo ipertesto!
Esempio 6.6: A che pressione bolle l'acqua alla temperatura di 37°C? E di 200°C?
Basta ricordare che, per l'acqua, λev = 539 kcal/kg = 539 x 4186 x 0,018 = 40,6 kJ/mol. Poiché a P1 = 1 atm l'acqua bolle a 100°C, usando la precedente si ricava che a T2 = 37°C corrisponde la pressione di P1 = 0,07 atm, e a T2 = 200°C corrisponde a P1 = 16 atm.
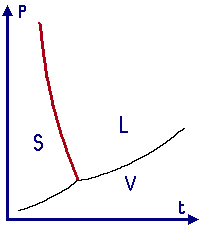
Rappresentando l'andamento di P = P(T) in funzione della temperatura, per le sostanze per cui ΔV > 0 (ad esempio la CO2, l'NH3...) l'andamento è quello qui sotto a sinistra. Ciò, però, non è affatto valido per l'acqua, poiché è risaputo che il ghiaccio, sciogliendosi, diminuisce di volume. Per l'acqua insomma il ΔV è negativo, e la curva corrispondente è quella qui sotto a sinistra:


La conseguenza è che il ghiaccio galleggia; si capisce facilmente che, se non fosse così, la biosfera non potrebbe mai mantenersi meteorologicamente stabile, perchè gli oceani comincerebbero a ghiacciare dal fondo. Lo ha intuito persino questo versetto del Corano:
« Dall'acqua Allah ha creato tutti gli animali. Alcuni di loro strisciano sul ventre, altri camminano su due piedi e altri su quattro. » (Sura XXIV, 45)
Questo comportamento anomalo è dovuto ai legami idrogeno che essa stabilisce tra le proprie molecole. Essi reclamano precise direzioni spaziali, e così si spreca volume nel realizzare il solido, cioè il ghiaccio, che aumenta di volume rispetto al liquido, a causa degli spazi vuoti rimasti tra le molecole. Questo spiega tra l'altro perchè l'acqua (H2O) bolle a + 100°C, mentre l'acido solfidrico (H2S) bolle a – 60°C, nonostante lo zolfo nella tavola periodica si trovi esattamente sotto l'ossigeno, e dunque essi dovrebbero avere proprietà chimiche molto simili. Lo zolfo infatti non forma legami idrogeno, a differenza dell'ossigeno, e dunque occorre molta meno energia per disgregare il solido, facendolo passare allo stato liquido!
Come si vede qui sotto, i due diagrammi soprastanti sono dei particolari dei diagrammi di stato da noi già disegnati nel capitolo 2; gli altri due tratti si disegnano tenendo conto che il ΔV di ebollizione e di sublimazione è comunque positivo per tutte le sostanze.

Aggiungiamo (perchè ci servirà più avanti) che una relazione analoga alla (6.12) può essere scritta anche per l'Energia Libera di Helmholtz. Sappiamo infatti che A = U – T S; differenziando ambi i membri di tale equazione si ha:
dA = dU – T dS – S dT
Tuttavia si è scritto sopra che:
dU = T dS – P dV
Sostituendola nella precedente si ottiene:
dA = – P dV – S dT (6.14)
Tale relazione vale per le trasformazioni isotermocore.
.
6.8 Il Ciclo Rankine
Come si è detto, il Ciclo di Carnot costituisce il ciclo con il rendimento migliore di tutti, però non è tecnicamente realizzabile, vuoi per la difficoltà a realizzare le isoterme, vuoi per la sua pretesa di reversibilità. Infatti, come è noto, è ben difficile realizzare trasformazioni isoterme, dovendosi ogni volta sottrarre un lavoro pari al calore fornito, e viceversa. Tuttavia, come sappiamo, esiste una situazione in cui gli scambi di calore avvengono in una situazione perfettamente isoterma: i cambiamenti di fase. L'idea è troppo attraente perchè non si cerchi di sfruttarla a fini tecnologici; nacque così la proposta di sostituire alle isoterme del Ciclo di Carnot due isotermobariche, cioè di farlo avvenire non con gas perfetti, bensì con fluidi reali al di sotto della Campana di Andrews, in questo modo:
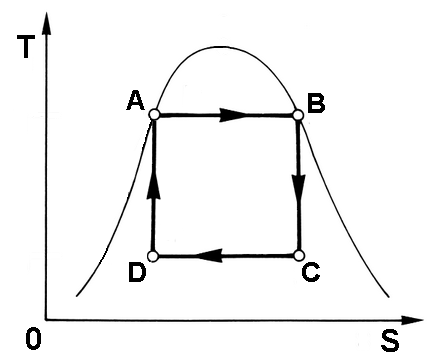
Quello così concepito è chiamato Ciclo di Rankine, in onore del suo ideatore, l'ingegnere scozzese William John Macquorn Rankine (1820-1872), ed è il ciclo comunemente utilizzato nelle moderne termoelettriche e termonucleari.
Il problema è che, come apprendiamo con sorpresa, anche questo ciclo è... irrealizzabile! Infatti il fluido sotto la Campana di Andrews è costituito da una miscela di liquido e di vapore, come abbiamo fatto nel § 3.4, e la sola idea di comprimere tale miscela (il tratto DA) è completamente da scartare per motivi tecnologici. È necessario spostare il tratto DA più a sinistra, e comprimere il solo liquido mediante una normale pompa. Il ciclo assume allora l'aspetto qui sotto, finalmente realizzabile tecnicamente:

Il tratto EA è assai più corto del tratto CD, perchè il liquido è praticamente incomprimibile. Così congegnato, però, il ciclo ha un rendimento assai minore di quello di Carnot, perchè nel tratto AB in fase liquida il calore non è fornito a temperatura costante. Per cercare di aumentare il rendimento, si sceglie allora di operare un surriscaldamento: si porta cioè il fluido, ora vapore, ad una temperatura ben più alta di quella di ebollizione, per poi far espandere il vapore surriscaldato così ottenuto. Si ha in tal modo il ciclo seguente:
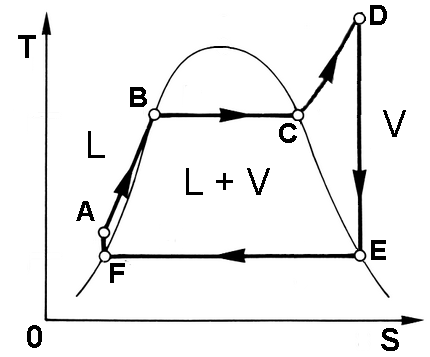
ABCD è un riscaldamento isotermobarico, in cui il fluido è posto a contatto con una sorgente di calore. Da A a B il fluido è ancora in fase liquida; da B a C si ha la transizione di fase; da C a D si ha solo vapore. Si osservi che questo riscaldamento non è ideale, potendosi fare mettendo il contatto il fluido di lavoro con un gas caldo, ad esempio i fumi di combustione in caldaia, che viaggiano in senso inverso, da D ad A, e cedono il loro calore al fluido del ciclo. Questo viene fatto all'interno della caldaia.
Da D ad E si ha un'espansione adiabatica, che avviene in turbina. È qui che dal fluido si estrae lavoro meccanico. Da E ad F si ha invece un raffreddamento isotermobarico, in cui si ha la trasformazione di fase inversa, fino allo stato di liquido saturo (in F). Ciò avviene in uno scambiatore di calore con l'ambiente esterno. Da F ad A infine si ha una compressione adiabatica del fluido interamente in fase liquida, grazie ad una pompa. Lo schema dell'impianto così realizzato è quello sottostante.

In realtà, anche qui c'è un problema: infatti, come si vede in figura, il tratto DE attraversa la campana di Andrews, e quindi in turbina si formano gocce d'acqua che possono letteralmente distruggere le pale della turbina. È un problema grave, cui si tenta di ovviare con varie soluzioni tecnologiche.
Naturalmente, il rendimento così ottenuto è ancora basso: si pensi che il ciclo Rankine di una normale locomotiva a vapore tipo Far West non raggiunge il 15 %! Siccome però quello era un ciclo destinato alla propulsione, non all'ottenimento di energia elettrica, poteva bastare per raggiungere buone velocità. Nei moderni impianti termoelettrici, invece, ciò non è più tollerabile. Allora, per cercare di alzare il rendimento, e contemporaneamente per cercare di diminuire il numero di gocce di liquido in turbina, si provvede alla rigenerazione:
Ciò significa questo: l'area del Ciclo Rankine è certamente inferiore a quella del Ciclo di Carnot; tuttavia, se riuscissi a realizzare un circuito come quello qui sopra, esso avrebbe la stessa area, e quindi più o meno lo stesso rendimento. Questo risultato può essere ottenuto sottraendo calore al fluido in espansione, in modo che l'espansione in turbina non sia più adiabatica a temperatura costante. Ciò è possibile ponendo a contatto diretto il fluido che si raffredda con quello che si riscalda, in modo da risparmiare calore "aiutando" l'altro tratto del ciclo ad arrampicarsi; o, come si fa più spesso nei cicli reali, spillando una parte del fluido dalla turbina e miscelandolo con il fluido che si sta riscaldando. Si parla allora di Ciclo Rankine con spillamenti. In realtà, esso è formato da tanti cicli sovrapposti quanti sono gli spillamenti, come si vede qui sotto, con due o più turbine a vapore ed altrettante pompe; in tal modo il rendimento può arrivare a sfiorare il 40 %. Tale era ad esempio il Ciclo Rankine della grande centrale nucleare italiana di Trino Vercellese.

.
6.9 Ciclo Otto e Ciclo Diesel
Dopo aver presentato il Ciclo Rankine, non possiamo fare a meno di presentare un altro ciclo comunissimo e di larghissimo uso: il Ciclo Otto, normalmente usato nei motori a combustione interna (detti anche motori a scoppio o motori a quattro tempi) delle nostre automobili. Esso prende il nome dall'ingegnere tedesco Nikolaus August Otto (1832-1891) che depositò il brevetto di questo motore nel 1876; il primo prototipo era però stato messo a punto dai lucchesi Eugenio Barsanti (1821-1864) e Felice Matteucci (1808-1887) già nel 1853. Nel 1861 poi l'inventore francese Alphonse Beau de Rochas (1815-1893) aggiunse la fase di compressione al motore di Barsanti e Matteucci.

Francobollo celebrativo di Barsanti e Matteucci (da questo sito)
Vale la pena di dire qualcosa a proposito di questi due geni a lungo dimenticati, che precorsero di gran lunga Nikolaus Otto e Rudolf Diesel. Nicolò Barsanti nacque a Pietrasanta (Lucca) e divenne sacerdote dell'ordine degli Scolopi, assumendo il nome di Eugenio dell'Addolorata. E ciò non deve stupire, perchè anche Niccolò Copernico, Ruggero Boscovich e Gregor Mendel erano allo stesso tempo preti e scienziati. Nel 1841 iniziò a insegnare fisica al Collegio San Michele di Volterra, ed è qui che, nella primavera del 1843, gli venne l'idea base dell'invenzione del motore a scoppio. Durante un esperimento in aula riempì un contenitore con una miscela gassosa e lo sigillò con un tappo di sughero, poi fece scoccare in esso una scintilla: la fiamma incendiò i gas, aumentandone il volume, e questo provocò uno scoppio che fece saltare il tappo. Non era la prima volta che si osservava questo fenomeno, ma Barsanti fu il primo ad avere l'idea di usarlo per trasformare l'energia termica in energia meccanica, facendo girare un motore, e fu il primo a capire che questo motore sarebbe stato più efficace e meno ingombrante di quelli a vapore.
Nel 1845 Barsanti cominciò a insegnare all'Osservatorio Ximeniano, importante istituto scientifico di Firenze. Qui fece amicizia con un altro illustre ingegnere, il lucchese Felice Matteucci. Quest'ultimo è stato definito da un biografo « il lato oscuro di Barsanti »: era introverso, insicuro e malato di depressione. Ma era un grande esperto di ingegneria idraulica e meccanica, così Barsanti vide in lui il collaboratore ideale per lavorare sul suo motore; iniziò così la loro feconda collaborazione, che in pochi anni portò alla realizzazione di una macchina in grado di ripetere ciclicamente la trasformazione della forza esplosiva in meccanica. Grazie all'appoggio delle Officine del Pignone di Firenze, il motore fu realizzato nel 1853. Ma non esisteva un ufficio brevetti nazionale,perché l'Italia unita non esisteva ancora. I due decisero di brevettare l'invenzione in Inghilterra, la patria della Rivoluzione Industriale; però servivano tempo e denaro, e i due inventori non ne avevano. E così l'ufficio londinese bocciò il progetto, e parte della documentazione di Barsanti e Matteucci andò perduta. I due però non si arresero: nel 1856 costruirono un nuovo prototipo, nelle officine della Ferrovia Maria Antonia. Stavolta andò meglio: nel 1857 la Società Lariana di Navigazione a Vapore, con sede a Como, chiese loro di realizzare un propulsore per i propri battelli con la potenza di 8 cavalli, perfettamente funzionante ma troppo poco potente per la navigazione. Nel 1859 si trasferirono nel Regno di Sardegna, fondarono una società e provarono a buttarsi nel business delle ferrovie. Un nuovo modello da 12 cavalli del loro motore fu presentato nel 1861 all'Esposizione Nazionale di Firenze e sembrò segnare una svolta: si fecero avanti aziende e imprenditori, italiani ed esteri.

Modello del motore Barsanti-Matteucci all'Osservatorio Ximeniano di Firenze
Ma, proprio quando le cose sembravano mettersi sulla buona strada, nel 1862 Matteucci, la cui depressione era stata aggravata da tutte queste traversie, decise di uscire dalla società, lasciando solo Barsanti, che purtroppo stava diventando cieco. Nonostante questo, egli continuò a lavorare giorno e notte: nel 1863 uscì dalle Officine Bauer di Milano l'ultimo prototipo. Funzionava così bene che un'azienda belga, la John Cockeril, si offrì di produrlo in serie. Ma il 19 aprile 1864 Barsanti morì improvvisamente a Seraing, vicino a Liegi. Matteucci morì a sua volta nel 1887, dimenticato da tutti. Nel frattempo, Nikolaus Otto aveva brevettato il suo motore a combustione interna, ottenendo un tale successo che da allora il suo nome fu inscindibilmente legato ad esso ("Ciclo Otto"); e un altro tedesco, Karl Friedrich Benz (1844-1929), aveva cominciato a produrre la Patent Motorwagen, la prima "carrozza senza cavalli" dotata di un motore a scoppio. Tranne pochi dettagli, tale motore era praticamente identico all'ultima versione progettata da Barsanti. Coincidenza o plagio? Nessuno lo sa. Quel che è certo è che l'affermazione del motore tedesco fu strepitosa, mentre del sacerdote-inventore di Pietrasanta e del suo collega malato di depressione si perse a lungo ogni memoria. Del loro lavoro è rimasto ben poco, perché molti documenti e tutti i prototipi sono andati perduti, ma nel 2003, grazie agli sforzi della Fondazione Barsanti e Matteucci, un gruppo di studiosi ha ricostruito il motore che i due avevano ideato nel 1853, restituendo all'Italia il giusto primato, anche se con 150 anni di ritardo.
Vale la pena di aggiungere un'altra curiosità interessante. Carlo Menon (1858-1924) era un industriale nato a Roncade, in provincia di Treviso, il quale, in società con un amico, l'ingegnere milanese Cervasoni, cercò di ideare un aeroplano a pedali, come le biciclette di cui si era occupato fino ad allora. Come racconta suo figlio, Luigi Menon, in un diario pubblicato solo nel 1985, si trattava di un triciclo con gomme pneumatiche i cui pedali, anziché agire sulle ruote, facevano girare un'elica a quattro pale che avrebbe dovuto far alzare l'aereo. un biplano con apertura alare di 10 metri. I migliori ciclisti riuscirono a far correre a terra l'apparecchio con qualche saltino: potenza insufficiente, riconobbero Menon e Cervasoni. Tentarono con un cavallo veloce sulla strada principale del paese, e l'aereo si alzò da terra per qualche metro, ma un velivolo a cavalli non aveva senso e dunque si pensò ad un motore potente e leggero, un « De Dion Bouton » francese che pesava una cinquantina di chilogrammi e che dava una potenza di 2,5 cavalli vapore. Fu subito acquistato ma intanto la società, gravata di tutte le spese sostenute, fallì. L'ingegner Cervasoni tornò a casa deluso, ma Menon non si scoraggiò e montò il prezioso motore su una carrozza. Funzionò e nacque così la « Vetturetta », in grado, con i successivi adattamenti, di viaggiare a 35 chilometri orari. Oggi si discute se essa fu il primo mezzo a quattro ruote motorizzato realizzato in Italia, perché il veronese Enrico Bernardi (1841-1919) negli stessi anni concepì qualcosa di analogo (ma con tre ruote). La Vetturetta in ogni caso divenne famosa e comparve anche in alcuni film, ma in seguito se ne persero le tracce. Anche in Italia era finita l'era dei pedali e della macchina a vapore, e cominciava quella del motore a scoppio.
Vediamo dunque di spiegare come funziona il ciclo ideato dai due geni lucchesi, e sfruttato dall'intraprendente trevigiano. Esso avviene in un cilindro dotato di pistone come quello illustrato qui sotto: il pistone è collegato a un albero mediante un sistema biella-manovella, che trasforma il moto alternativo del pistone in moto rotatorio, trasmesso poi alle ruote dell'automobile. Il cilindro è dotato di valvole di immissione del carburante e di valvole di scarico dei gas combusti, oltre ad una candela elettrica in grado di far scoccare una scintilla. Come si vede, il motore funziona attraverso quattro fasi o tempi, che in questa animazione si vedono numerate da 1 a 4:
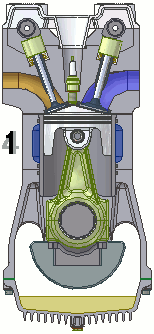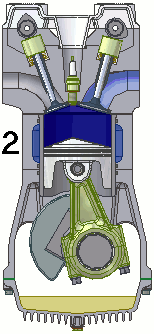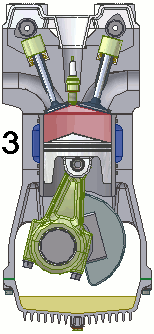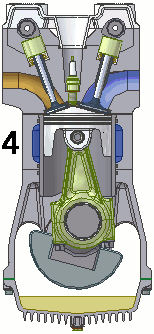
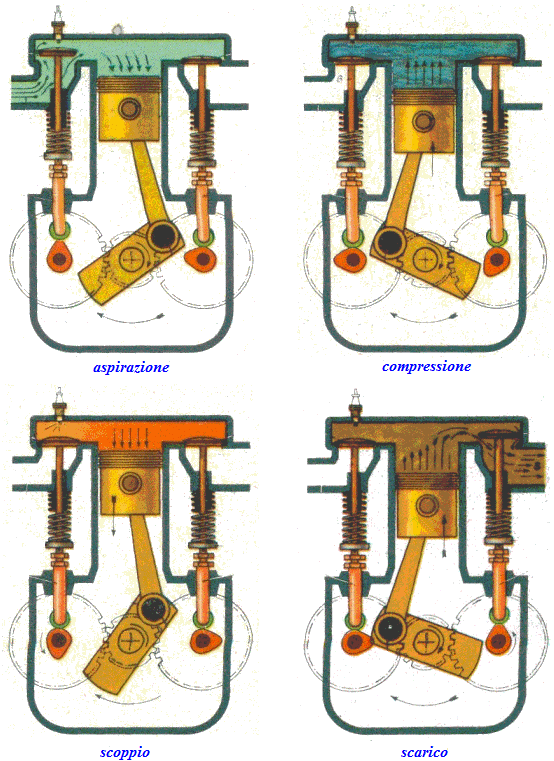
1a fase (aspirazione): lo stantuffo si muove verso il basso e crea una depressione; si apre la valvola di immissione ed il combustibile, proveniente dal carburatore, è aspirato dentro il cilindro.
2a fase (compressione): dopo essere arrivato a fine corsa, cioè a quello che si chiama il punto morto inferiore, il pistone torna su spinto dall'albero; entrambe le valvole sono chiuse e la miscela viene fortemente compressa.
3a fase (scoppio ed espansione): quando il pistone raggiunge il punto più alto della sua corsa, cioè a quello che si chiama il punto morto superiore, la candela fa scoccare una scintilla, e ciò provoca l'esplosione della miscela che si espande e spinge il pistone verso il basso.
4a fase (scarico): il pistone risale e la valvola di scarico si apre, cosicché i gas combusti vengono spinti fuori, verso il tubo di scappamento.
Si osservi che una sola fase è attiva, cioè è in grado di spingere il pistone: lo scoppio. Ma un intero ciclo dura ben due giri completi dell'albero. Per assicurare il funzionamento continuo del motore, sull'albero sono calettati quattro cilindri che si trovano ciascuno in una fase diversa, in modo che contemporaneamente il primo sarà in fase di aspirazione, il secondo in fase di compressione, il terzo in fase di scoppio ed il quarto in fase di scarico. Subito dopo il primo passerà in fase di compressione, il secondo di scoppio, il terzo di scarico e il quarto di aspirazione; e così via. Il moto dell'albero motore comanda anche le valvole e la candela. Infatti l'albero motore è collegato a due alberi a camme, visibili nell'animazione qui sopra, che ruotando aprono e chiudono le valvole di immissione e di scarico in perfetta sincronia con le fasi del motore a scoppio. Anche le candele emettono una scintilla nel momento giusto, cioè in corrispondenza alla fine della fase di compressione, grazie ad uno strumento chiamato spinterogeno, anch'esso collegato all'albero motore.
Ora, la seconda e la terza fase si possono assimilare rispettivamente a una compressione e ad un'espansione adiabatica, mentre la prima e la quarta, nell'ipotesi che il pistone sia pressoché fermo nei punti morti inferiore e superiore, si approssimano rispettivamente con un raffreddamento isocoro e un riscaldamento isocoro. Il Ciclo Otto dunque risulta formato da due isocore e due adiabatiche, e lo si rappresenta in questo modo nei piani di Clapeyron e di Gibbs:

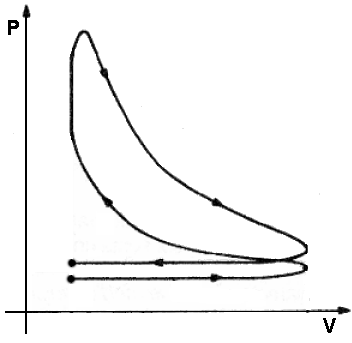
In realtà, il ciclo ora tracciato è assolutamente ideale e il gas in esso non cambia mai. Invece, nel ciclo Otto la miscela di carburante e ossigeno proveniente dal carburatore viene completamente bruciato, e non si possono reimmettere nel cilindro i prodotti di combustione per chiudere il ciclo. Il Ciclo Otto reale insomma è aperto, e viene rappresentato come nella figura sottostante:
Esiste un'altra versione del Ciclo Otto, il cosiddetto motore a scoppio a due tempi. Esso funziona attraverso due sole fasi, durante il quale l'albero motore compie un giro solo, da cui il nome. Il cilindro possiede tre aperture prive di valvole, chiamate luci di immissione, di lavaggio e di scarico. Esse sono aperte e chiuse non dalle valvole, come nel motore a quattro tempi, ma dal pistone stesso durante il suo movimento. Senza valvole, mancano gli alberi a camme, mentre la presenza della candela per incendiare la miscela richiede uno spinterogeno. Il pistone, inoltre, possiede uno speciale profilo deflettore che ha il compito di evitare la mescolanza dei gas combusti con la miscela fresca. La miscela non passa direttamente dal carburatore al cilindro, ma viene prima aspirata e compressa nel carter, cioè nella porzione del cilindro al di sotto del pistone, dove ruota il sistema biella-manovella. Come si vede qui sotto, nella prima fase, all'inizio della corsa verso il punto morto inferiore, la luce di lavaggio si apre e la miscela fresca che si trova nel carter viene compressa e spinta nel cilindro, al di sopra del pistone. Nel contempo si apre la luce di scarico e la miscela fresca che entra effettua il lavaggio, contribuendo a spingere fuori i gas combusti del ciclo precedente. In fase di risalita le luci di lavaggio e di scarico si chiudono e ha inizio la compressione, mentre si apre la luce di immissione, al di sotto del pistone, che richiama la miscela dal carburatore entro il carter per effetto della depressione generata dalla salita del pistone. Quando il pistone è quasi giunto al punto morto superiore, si verifica lo scoppio ed inizia la seconda fase. Spinto dai gas che si espandono, il pistone inizia la corsa verso il basso ed apre prima la luce di scarico, attraverso la quale i gas combusti sono pompati verso il tubo di scappamento, e poi quella di lavaggio, attraverso la quale inizia l'ingresso della miscela fresca che si completerà, durante la successiva risalita.
Nonostante nel motore a due tempi si abbia una fase attiva ogni giro, anziché ogni due come in quello a quattro tempi, a parità di cilindrata la potenza ottenuta è inferiore. Ciò dipende, fra l'altro, dall'impossibilità di un perfetto riempimento del cilindro (fughe di miscela fresca dalla luce di scarico, presenza di residui di gas combusti) e dal fatto che la luce di scarico si apre quando è ancora in atto l'espansione dei gas combusti. Per questi motivi questo ciclo è stato oggetto di numerosi perfezionamenti, dall'introduzione di un sistema di valvole di distribuzione, come nel motore a quattro tempi, all'utilizzo di camere di precompressione per la miscela da introdurre nel cilindro. Essendo privo di alberi a camme, il motore a scoppio a due tempi è più semplice da realizzare di quello a quattro tempi ed occupa meno spazio, per cui è solitamente installato sui ciclomotori e nei motori fuoribordo.

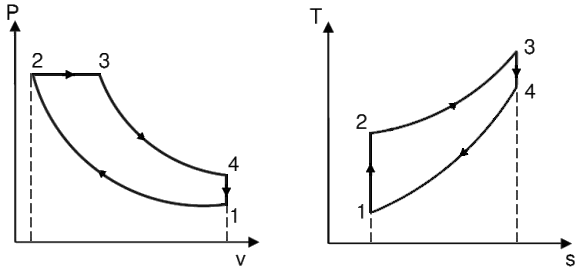
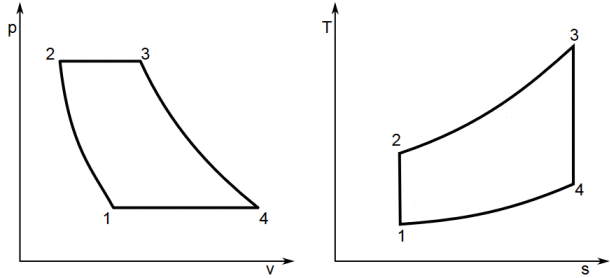
Un altro ciclo molto utilizzato è il Ciclo Diesel, così detto dal suo inventore, il tedesco Rudolf Diesel (1858-1913), che lo mise a punto nel 1892. Esso, a differenza del Ciclo Otto, è formato da due adiabatiche, un'isocora e un'isobara, come si vede nei diagrammi sottostanti, perchè la fase di scarico avviene a volume costante, non a pressione costante, anche se in realtà anch'esso è un ciclo aperto, non potendosi bruciare nuovamente il combustibile esausto. Il suo ciclo viene svolto in due giri di albero motore, e comprende delle valvole mosse dall'albero a camme, come nel motore a scoppio, ma è privo di candele. Infatti lo scoppio avviene per mera compressione del combustibile, che non è più benzina come nel Ciclo Otto, ma gasolio, molto più facilmente infiammabile. Questo però richiede un rapporto di compressione molto maggiore di quello del Ciclo Otto, proprio perchè il combustibile va compresso molto più fortemente, per esplodere senza bisogno di scintille. Con il termine rapporto di compressione si intende il rapporto tra il massimo ed il minimo volume del cilindro, cioè tra quello misurato al punto morto inferiore e quello misurato al punto morto superiore; per il Ciclo Otto esso vale circa 8, mentre per il Ciclo Diesel esso deve valere almeno 20. L'assenza di candele comporta l'assenza dello spinterogeno; tuttavia, i moderni motori Diesel contengono le cosiddette candelette di preaccensione, che riscaldano la miscela favorendone lo scoppio. Sempre nei motori Diesel moderni si ricorre alla cosiddetta sovralimentazione, onde introdurre una maggior quantità di ossigeno all'interno della camera di scoppio per poter bruciare una maggior quantità di combustibile ad ogni ciclo. Per ottenere questo risultato si ricorre ad un turbocompressore collegato al collettore di aspirazione: esso comprime l'aria che verrà immessa poi nel cilindro. Il compressore centrifugo è trascinato dalla turbina a gas di scarico calettata sullo stesso asse, che espande i gas combusti in uscita dal cilindro del motore.
Esiste anche un Ciclo Diesel a due tempi, oggi impiegato quasi esclusivamente per la propulsione delle navi: il suo ciclo corrisponde ad un giro di albero motore esattamente come nei motori a scoppio a due tempi, ed è detto anche Ciclo Sabathé. In esso la combustione avviene in parte a pressione costante ed in parte a volume costante.
Un altro ciclo di interesse industriale è il Ciclo Stirling, così detto dall'inventore scozzese Robert Stirling (1790-1878), che nel 1816 inventò il cosiddetto Motore a Combustione Esterna. Questo ciclo è formato da due isoterme e due isocore, e il calore viene trasmesso al fluido attraverso uno scambiatore (da cui il nome di "motore a combustione esterna"). Il motore funziona a ciclo chiuso utilizzando un gas come fluido termodinamico, solitamente aria, oppure, nelle versioni ad alto rendimento, idrogeno o elio. Quando è raggiunta una sufficiente differenza di temperatura tra la sorgente calda e la sorgente fredda, si innesca una pulsazione ciclica, trasformata in moto alternato dai pistoni. La pulsazione perdura finché si mantiene la differenza di temperatura, assorbendo calore dalla sorgente calda e cedendone alla sorgente fredda. L'assenza di contatto diretto fra la miscela dei gas combusti e tutte le parti meccaniche in movimento ne riduce l'usura, la necessità di lubrificazione e la conseguente manutenzione. Il motore inoltre non ha valvole e non subisce scoppi, quindi è più semplice, con vibrazioni più facilmente controllabili e molto meno rumoroso di un motore a combustione interna. Il motore Stirling può essere alimentato con una qualsiasi fonte di calore, e cioè la combustione di legna, carbone, gas, biogas, combustibili liquidi, energia solare ed energia nucleare. Tuttavia la combustione esterna, richiedendo scambiatori di calore sia alla sorgente calda sia alla sorgente fredda, rende il motore di Stirling in generale più ingombrante e pesante di un generico motore a combustione interna a parità di potenza erogata, e il suo avviamento è lento. Inventato come evoluzione dei motori ad aria calda usati in Inghilterra durante la Prima Rivoluzione Industriale, nel 1950 l'olandese Philips realizzò un piccolo generatore elettrico basato su una unità Stirling a combustione di petrolio, con una potenza di circa 200 Watt, che veniva usato per alimentare apparecchi radiofonici dislocati in località remote, prive di alimentazione elettrica.
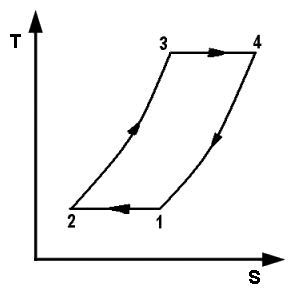
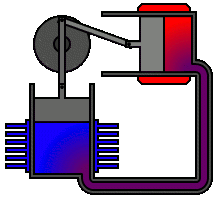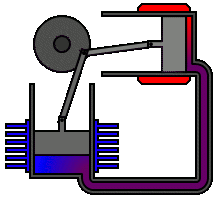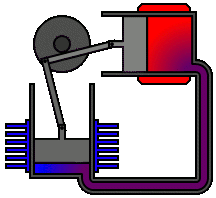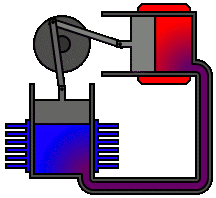
Il Ciclo Ericsson, ideato nel 1829 dall'inventore svedese John Ericsson (1803-1889), è invece formato da due isoterme e due isobare, e si compone di 4 fasi: compressione isoterma, riscaldamento isobaro, espansione isoterma e raffreddamento isobaro. Molto simile ad esso, infine, è il cosiddetto Ciclo Brayton, così detto perchè brevettato nel 1872 dall'ingegnere statunitense George Brayton (1830-1892). Esso si compone di due adiabatiche e due isobare, e comprende quattro fasi: compressione adiabatica del gas in un compressore, riscaldamento isobaro, espansione isoentropica del gas in una turbina, raffreddamento isobaro. I motori Brayton sono a combustione interna e a ciclo aperto: il compressore aspira aria dall'ambiente aumentandone la pressione senza scambi di calore con l'esterno; si inietta il combustibile che brucia alzando la temperatura del fluido, ma non la pressione che invece resta costante; il fluido caldo si espande in una turbina cedendo ad essa lavoro meccanico e diminuendo la propria pressione e temperatura; infine, il fluido uscente dalla turbina a pressione ambiente si raffredda nell'atmosfera.
Si basa sul ciclo Brayton il funzionamento del turbocompressore, noto semplicemente come "motore turbo". Esso deve il suo nome al fatto che è costituito da un compressore trascinato da una turbina, azionata dai gas di scarico del motore; per funzionare, quindi, non assorbe potenza dal motore. Il motore turbo è infatti composto da un corpo centrale di sostegno e due chiocciole; nella chiocciola di scarico è contenuta una turbina detta impeller azionata dai gas di scarico, che trasmette il suo movimento tramite un albero alla girante racchiusa nella chiocciola opposta, la quale comprime l'aria aspirata funzionando da compressore. A causa della sua altissima velocità di rotazione, che arriva a 600 m/s, la girante è soggetta a forti sollecitazioni meccaniche, che impongono un'elevata resistenza strutturale dei materiali. Nella turbina l'aria viene fortemente accelerata e, per effetto del campo centrifugo, subisce una forte compressione, con conseguente innalzamento della sua temperatura fino a quasi 300°C. Anche questo ciclo in realtà è aperto, perchè i gas combusti non possono certo rientrare in ciclo. Il primo motore turbo fu messo a punto nel 1885 dall'ingegnere tedesco Gottlieb Daimler (1834-1900), e successivamente brevettato dallo svizzero Alfred Büchi (1879–1959) nel 1905. I piccoli motori turbo per impiego automobilistico apparvero negli anni '60, per iniziativa di alcuni costruttori come l'Alfa Romeo, e in seguito furono largamente adottati nelle competizioni automobilistiche, poiché garantivano prestazioni elevatissime.

.
Se non vi ho stancato con questa lunga cavalcata attraverso i cicli disegnati nel Piano di Gibbs e nel diagramma di Mollier, vi consiglio di cliccare qui e di passare con me al prossimo capitolo, nel quale vedremo come quella strana grandezza chiamata entropia è connessa al concetto di probabilità. Per tornare all'indice, invece, il link è questo.
![]()