Entropia e probabilità

Quello di entropia è un concetto assai difficile; tuttavia, l'opportunità di introdurlo è giustificata dall'efficacia con cui, tramite questo, vengono interpretati i fenomeni termodinamici e risolti i problemi ad essi connessi. Ciò deriva dalle notevoli proprietà possedute da questa funzione di stato, a partire dall'uso del piano di Gibbs che, come si è visto, semplifica in maniera incredibile la trattazione di certi cicli, come il Ciclo di Carnot. Ma non solo: infatti, poiché tutti i processi naturali sono irreversibili, ogni processo naturale conduce sempre un sistema isolato in uno stato finale in cui l'entropia è maggiore di quella corrispondente allo stato iniziale. L'evoluzione spontanea di un sistema isolato può avvenire solo con una crescita di entropia, a patto che il sistema non scambi energia con l'esterno. L'esistenza dei frigoriferi non contraddice questo principio, poiché la sottrazione di calore dalla cella frigorifera comporta sì una diminuzione di entropia in essa, ma questo processo richiede energia, fornita dalla rete elettrica; per produrre tale energia si è dovuto bruciare del petrolio o far fissionare dell'uranio o far cadere masse d'acqua da alta quota, tutti processi che comportano sostanziali aumenti di entropia. Ebbene, l'aumento di entropia dovuto alla combustione di una certa quantità di barili di petrolio è senz'altro maggiore della diminuzione di entropia dovuta al raffreddamento della cella frigorifera, per cui complessivamente l'entropia dell'universo nel suo complesso è aumentata, salvaguardando il Secondo Principio. L'universo si dirige spontaneamente verso lo stato di entropia massima, e ciò è in accordo con il significato del termine "entropia" (in greco ἐντροπή), che tra l'altro significa "dirigersi".

Notiamo anche che un aumento di entropia corrisponde ad una perdita in quanto a capacità di produrre lavoro. Infatti, i processi che hanno portato all'aumento di entropia avrebbero potuto dare luogo alla produzione di lavoro meccanico, che invece non c'è stata. Per esempio, l'espansione libera di un gas, che aumenta l'entropia dell'universo, avrebbe potuto muovere uno stantuffo o far girare una turbina, ma non lo ha fatto. In tal modo, si può affermare che tutte le volte che l'entropia aumenta, si perde la capacità di produrre lavoro. È vero che, se si fornisce calore ad un gas, la sua entropia aumenta, ma esso ha aumentato la propria pressione e quindi è aumentata la sua potenziale capacità di produrre lavoro in una turbina; in ogni caso, siccome l'entropia può solo aumentare, il lavoro utilizzabile nell'universo può solo diminuire. Se per esempio consideriamo una fonte di calore a 300°C (ad es. l'acqua di soffioni boraciferi) ed una sorgente fredda a 0°C (ad es. l'acqua di un lago in inverno), e le utilizziamo per produrre lavoro meccanico mediante un ciclo termodinamico, io sottraggo del calore dalla fonte calda per cederla alla sorgente fredda; esse NON sono sorgenti ideali nel vero senso della parola, per cui la temperatura della sorgente calda ben presto scende, ad esempio ad 80°C, mentre quella della sorgente fredda sale a 15°C. Per il Teorema di Carnot, il lavoro che si può ricavare da questa situazione è assai minore di quello che si poteva ricavare prima, per cui il fatto di estrarre del lavoro inficia la possibilità stessa di produrre ulteriore lavoro.

Ciò significa che l'universo va verso quella che Clausius chiamò la morte termica, cioè uno stato di entropia massima, in cui ogni punto dell'universo si trova alla stessa temperatura, e dunque non è più possibile ricavare neppure un Joule di lavoro meccanico. Infatti, se T₁ = T₂, il rendimento di Carnot è pari a zero, e quindi il lavoro utile ricavabile è pari a zero. Questo concetto venne introdotto nel 1851 da Lord Kelvin, e ben presto divenne così popolare, da diventare sinonimo di "apocalisse". Ci fu chi cominciò a credere addirittura che la morte termica fosse imminente, che il sole si sarebbe spento ben presto e che la Terra sarebbe fatalmente morta di freddo. Il poeta romagnolo Giovanni Pascoli (1855-1912) fu talmente suggestionato da questa terribile prospettiva, da descrivere con accenti drammatici nella sua poesia "La Porta Santa" (compresa nella raccolta "Odi e inni" del 1906) la morte per consunzione dell'astro solare, ritenuta prossima ventura:

« Non ci lasciar nell'atrio
del viver nostro, avanti
la Porta chiusa, erranti
come vane parole;
ad aspettar che l'ultima
gelida e fosca aurora
chiuda alle genti ancora
la gran porta del Sole;
quando la Terra nera
girerà vuota, e ch'era
Terra, s'ignorerà. » (vv. 56-66)

Nella letteratura esiste un altro famoso riferimento a questa ipotesi in voga ai primi del Novecento: il mito di Cthulhu. Cthulhu è una creatura mitologica creata dalla fantasia dello scrittore statunitense Howard Phillips Lovecraft (1890-1937), e appare per la prima volta nel racconto "Il richiamo di Cthulhu" (1928). Si tratta di una creatura aliena di aspetto abominevole, giunta sulla Terra quando l'evoluzione della vita su di essa era appena cominciata, che si sarebbe insediata nella perduta città sommersa di R'lyeh, sotto l'Oceano Pacifico. Lovecraft immagina di averne avuto notizia dal "Necronomicon", un misterioso manoscritto scritto dall'"arabo pazzo" Abdul Alhazred. Tale è la fama del "Necronomicon" che molti lettori si sono convinti della sua reale esistenza e lo hanno cercato davvero, ma grazie al Cielo esso esiste solo nella contorta fantasia di Lovecraft, così come Cthulhu e molte altre creature consimili. Cthulhu sarebbe un essere vagamente antropomorfo, con la testa simile a quella di un polpo: viscida, flaccida e circondata di tentacoli. La sua pelle avrebbe il colore di un cadavere, ed emetterebbe il tanfo pestilenziale della carne in decomposizione. Tra i tentacoli si apre la bocca, armata di tre denti acuminati, e il suo corpo sarebbe dotato di ali membranose e di poderosi artigli. Cthulhu contatterebbe gli esseri umani nel sonno, attraverso gli incubi, e così sia popoli antichi, sia creature non umane lo avrebbero divinizzato; il suo culto sarebbe esteso a tutta la Terra, dall'Arabia alla Groenlandia ed alla Nuova Zelanda. Lovecraft non creò un Mito di Cthulhu completo e coerente, come fecero invece Tolkien ed Asimov con le loro invenzioni fantastiche, ma altri scrittori suoi contemporanei riutilizzarono il suo mondo e le creature da lui inventate, fra cui Cthulhu, concorrendo a dare intima coerenza a questa mostruosa deità del male. Che c'entra questo orrore con la Termodinamica? Il fatto è che vari lettori hanno avanzato l'ipotesi che, nella mente di Lovecraft, Cthulhu sia proprio la personificazione del concetto di morte termica dell'universo. E non ci sarebbe da stupirsi, visto che queste demoniache creature avrebbero avuto come scopo la distruzione completa del cosmo, e nulla potrebbe rendere l'universo più inabitabile proprio della morte termica che aveva già turbato i sonni di Pascoli!

Anche Dante Alighieri era cosciente della corsa di tutte le realtà terrene verso la morte termica, come si evince da questi suoi versi del settimo canto del suo "Paradiso":

« Tu dici: "Io veggio l'acqua, io veggio il foco,
l'aere e la terra e tutte lor misture
venire a corruzione, e durar poco » (Par. VII, 124-126)

Come si arguisce da quanto sopra detto, il ragionamento condotto sinora per introdurre il concetto di entropia è alquanto influenzato dall'interesse economico di ottenere lavoro utile con il minimo dispendio possibile di energia; inoltre, sia la definizione che la valutazione operativa di tale fondamentale grandezza derivano dalla distinzione fra processi reversibili ed irreversibili.

D'altro canto, non conviene collegare, nella nostra mente, il concetto di irreversibilità con le capacità tecniche ed operative dell'uomo. Infatti se, in forza del progresso tecnologico dell'umanità, un processo attualmente irreversibile potesse diventare reversibile, tutta la logica del Secondo Principio, e quindi il concetto di entropia, che da esso deriva, crollerebbe di schianto, costringendoci a rivedere tutto l'impianto della Termodinamica. Ora, siccome è ragionevole credere che i principi che regolano l'universo (come la conservazione dell'energia e l'aumento dell'entropia) siano più vecchi della razza umana, sembra altrettanto ragionevole che siano indipendenti dall'osservatore, cioè... da noi. Bisogna perciò cercare di liberare l'entropia da una matrice "antropomorfa", definendola in un orizzonte che sia il più possibile svincolato dalle attuali conoscenze fisiche e tecnologiche dell'uomo.

A questo scopo, osserviamo che, mentre il Primo Principio della Termodinamica è una legge universale di validità assoluta, dai nuclei atomici agli ammassi di galassie, il Secondo Principio è prettamente "umano", cioè le ragioni che ci hanno condotto ad enunciarlo derivano quasi esclusivamente da osservazioni effettuate su sistemi formati da un numero enorme di molecole, escludendo quelli costituiti da un numero relativamente piccolo di particelle. La differenza è dunque abissale: la conservazione dell'energia vale anche per sistemi composti da una sola particella, mentre il secondo, potendosi applicare solo a sistemi composti da un gran numero di particelle, deve pur sempre presentare una logica marcatamente termodinamica, cioè macroscopica, altrimenti sarebbe privo di senso. Per chiarire questo problema, consideriamo due recipienti A e B contenenti un gas a temperatura e pressione uniforme, e comunicanti per mezzo di una paratia scorrevole, manovrabile senza alcun attrito. Immaginiamo ora, come fece James Clerk Maxwell con un suo famoso esempio, di immettere in questo sistema, inizialmente all'equilibrio termodinamico, un essere diabolico detto Diavoletto di Maxwell, in grado di tenere aperta la valvola solo quando una particella, durante il suo moto disordinato, sbatte contro la paratia con alta velocità dalla parte di A, o con velocità bassa dalla parte di B. In tal modo, ben presto tutte le molecole veloci passano da A a B, e tutte le molecole lente da B ad A. Come si sa i diavoli non mangiano, non bevono, non respirano, e dunque in tal modo si crea spontaneamente una diminuzione di entropia, perchè si è ottenuto uno squilibrio di pressione senza alcun bisogno di fornire lavoro dall'esterno. Analogamente, se il Diavoletto di Maxwell fa passare in B tutte le molecole veloci e in A tutte quelle lente, ben presto si otterrà una diminuzione di entropia con la situazione esattamente speculare rispetto alla precedente. In entrambi i casi il diabolico operatore, esercitando le sue capacità cognitive, ha trovato il modo di violare il Secondo Principio della Termodinamica. Certo, ci vorrà molto tempo, anzi moltissimo, ma i diavoli sono notoriamente immortali, ed hanno molta, anzi moltissima pazienza...

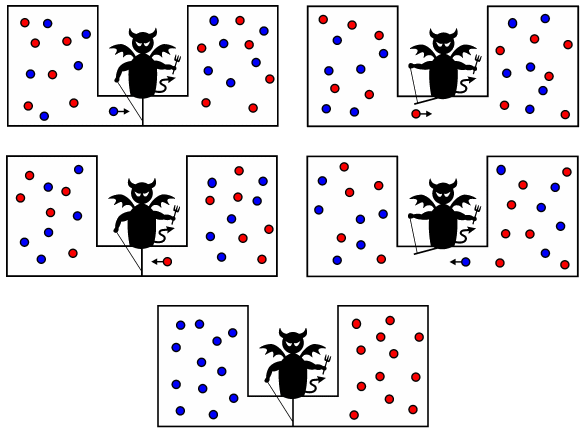
Naturalmente qualcuno di voi potrebbe chiedersi cosa ci fa un diavolo nella storia della Fisica, che è razionalista per eccellenza. Il fatto è che, al posto del diavolo, ci potrebbe essere un dispositivo automatico in grado di rilevare la velocità delle molecole e di aprire o chiudere la paratia a seconda delle molecole che si avvicinano, ottenendo la stessa diminuzione gratuita di entropia assicurata dal Diavoletto di Maxwell. Quello del Diavoletto ovviamente è un paradosso, e come tutti i paradossi deve avere una soluzione. A trovarla furono l'ungherese Leó Szilárd (1898-1964) e il francese Leon Brillouin (1899-1969) solo nel 1929, quindi 50 anni dopo la morte di Maxwell. Essi ragionarono così: anche ammesso che questo essere infernale, o qualunque apparecchio che ne faccia le veci, possa esistere davvero, il sistema gas + diavoletto non è affatto un sistema isolato, per cui il Secondo Principio è salvo. Infatti, per poter operare con cognizione di causa un processo selettivo sulle molecole, il diabolico organismo deve ricevere ogni volta delle precise informazioni sulla direzione e sulla velocità delle molecole; in altre parole, egli deve vederle. Per questo, egli deve poterle... illuminare con un fascio di luce o con qualcosa di simile. Anche al di là di tutte le considerazioni quantistiche che questo comporta (noi ci stiamo occupando di Fisica Classica), comunque deve esistere una sorgente di radiazioni esterna al gas. Ciò presuppone necessariamente un'interazione energetica con l'esterno: l'acquisizione di informazioni implica sempre un dispendio di energia. Allora, la diminuzione di entropia dovuta al lavoro del diavoletto è più che compensata dall'aumento di entropia della sorgente di energia. È vero che, per esserne sicuri dal punto di vista quantitativo, occorrerebbe conoscere qualcosa di più sul metabolismo degli esseri infernali; ma, siccome il diavoletto concepito da Maxwell è necessariamente umanoide, ritengo che, nonostante l'accanirsi contro di esso di tutti i diavoli dell'inferno, il Secondo Principio della Termodinamica continuerà a mantenere la propria validità, e Kelvin, Clausius e soci potranno godersi il meritato riposo eterno.

Resta però un problema da affrontare: una situazione del genere, con diminuzione spontanea di entropia, può per caso verificarsi anche spontaneamente, cioè senza alcun bisogno di diavoli?

Per rispondere a questa domanda, bisogna per la prima volta abbandonare l'impostazione termodinamica, cioè smettere di considerare i gas come corpi macroscopici descrivibili mediante variabili macroscopiche e basta, e bisogna cominciare a considerarli come aggregati di un grandissimo numero di particelle.

In assenza di diavoli, dobbiamo affidarci unicamente al caso per dirimere le nostre questioni. E il caso è governato dalle leggi della probabilità. Sappiamo che, secondo l'impostazione classica dovuta a Blaise Pascal (1623-1662) e Pierre de Fermat (1601-1665), la probabilità che un evento casuale abbia luogo è data dal rapporto tra il numero di casi favorevoli e il numero di casi possibili, nell'ipotesi che tutti gli eventi siano equiprobabili, cioè equivalenti l'uno all'altro nell'esperienza che si sta per compiere. Per esempio, se ho una moneta perfettamente simmetrica, è equiprobabile che essa sortisca testa o croce, per cui la probabilità che esca l'una o l'altra è 1/2 (un caso favorevole su due possibili).

Prendiamo ora in considerazione i recipienti A e B da noi introdotti per l'esperienza del Diavoletto di Maxwell. Teniamo sempre aperta la porticina ed aspettiamo del tempo, anche molto tempo (come si è detto, i diavoli sono insonni ed hanno un sacco di pazienza). Detto N il numero delle molecole, partiamo con N = 1. Allora ci sono solo due modi per disporle, una a destra ed una a sinistra:

La probabilità che la molecola sia in A, sia quella che sia in B, sono pari ad 1/2.

Se N = 2, le due molecole A e B si possono invece disporre in almeno quattro modi diversi:

A, B

La probabilità che entrambe le molecole siano in A è ora pari a 1/4 = 1/2².

.
Stavolta la probabilità che tutte le molecole siano in A è pari a 1/8 = 1/2³. Analogamente, se ho quattro molecole, avrò 16 stati possibili, e la probabilità che tutte le molecole si trovino in A scende a 1/16 = 1/2⁴. E così via, come si verifica facilmente.

Come si vede, più numerose sono le molecole, più è bassa la probabilità di trovarle tutte in A. In generale, N molecole si possono disporre in 2^N modi possibili. Ciascuna delle possibili disposizioni delle molecole prende il nome di microstato. Supponiamo che A, B, C, ecc... siano molecole identiche tra loro; allora, osservandole "dall'esterno", è a priori impossibile distinguerle l'una dall'altra. E così, nell'esempio qui sopra, tutti e tre i microstati che contengono due molecole a sinistra ed una a destra risultano indistinguibili. E se di molecole ne avessimo un numero sterminato, e segnatamente un numero di Avogadro? Indichiamo con P il numero dei microstati possibili in cui le molecole possono distribuirsi. Poiché quella da noi descritta è sostanzialmente un'espansione libera, è facile immaginare che, se parto da N molecole, esse si distribuiranno per lo più in modo da avere N/2 molecole nel recipiente A e N/2 nel recipiente B. In quanti modi possibili ciò può avvenire? O, in altri termini, da quanti microstati può essere composto il macrostato testé descritto? Il calcolo combinatorio ci insegna che i modi possibili in cui le N molecole possono essere disposte metà a sinistra e metà a destra dopo l'espansione libera sono le combinazioni senza ripetizione di N elementi a gruppi di N/2; tale numero è pari a:

Questi fattoriali sono enormi! Se N è molto grande, tuttavia, vale la cosiddetta formula di Stirling:

dove e è il numero di Nepero. La relazione (7.1) allora diventa approssimativamente:

E si riottiene così il risultato già ricavato precedentemente per via empirica. Ma questo vuol dire che la probabilità che tutte le molecole (il cui numero è dell'ordine del numero di Avogadro) si trovino dalla stessa parte della valvola è:

Questo numero è così assurdamente piccolo, da risultare indistinguibile dallo zero. In pratica, la probabilità di vincere i primi dieci premi della lotteria di Capodanno dopo aver acquistato in edicola solo dieci biglietti è infinitamente più grande di quella che abbiamo di morire soffocati perchè tutte le molecole d'aria della stanza in cui ci troviamo, in virtù del loro moto disordinato, sono uscite tutte dal buco della serratura!!

Da tutto ciò discende che, solo se il numero delle molecole è piccolo, il concetto di entropia è privo di significato. Se invece un sistema (come un gas) è formato da un numero davvero enorme di elementi, esiste una impossibilità pratica di violare i principi della Termodinamica, e quindi l'unidirezionalità dei processi reali.

Abbiamo dunque imparato una cosa molto importante: il fatto che un fenomeno avvenga spontaneamente in una direzione anziché in un'altra significa semplicemente che quest'ultima è più probabile rispetto alla prima. In altre parole, la Natura privilegia stati con probabilità maggiore rispetto a quelli a probabilità minore, esattamente come è possibile che si verifichi il caso di uno o due 100/100 per classe agli Esami di Maturità, anziché quello (davvero improbabile) di 25 voti massimi su 25. Ciò che vediamo verificarsi si verifica semplicemente perchè ha una probabilità maggiore di verificarsi rispetto al resto. Se il sistema è composto da pochi individui, questo risultato si presenterà in media; se questi sono numerosi, invece, si può star certi che si verificherà solo l'evento più probabile. Si può perciò fornire un nuovo enunciato del Secondo Principio:

SECONDO PRINCIPIO DELLA TERMODINAMICA, ENUNCIATO PROBABILISTICO: ogni sistema, abbandonato a se stesso, evolverà verso la situazione la ci probabilità è massima.

Per questo, tutti gli enunciati del Secondo Principio di cui abbiamo discusso nel capitolo 5 non dovrebbero cominciare con la dicitura « È impossibile... », bensì con le parole « È estremamente improbabile... » Per esempio, l'enunciato di Clausius suonerebbe così: « È estremamente improbabile realizzare una trasformazione termodinamica il cui unico risultato consiste nella cessione di calore da un corpo più caldo a uno più freddo » In teoria insomma potrebbe capitare un caso simile, ma siamo nella stessa situazione di una scimmia che batta a caso sui tasti di un personal computer. È stato calcolato che la probabilità che la scimmia scrittrice digiti sul computer la prima terzina della "Divina Commedia" di Dante Alighieri è solo una su 10 alla 134. Quest'ultimo è un numero grandissimo: basti pensare che le stelle dell'universo sono pari a 10 alla 22! È indubitabile che, aspettando abbastanza tempo, la scimmia finirà pure per digitare tutto il famoso incipit della Commedia dantesca, ma per battere quei 98 caratteri (spazi tra le parole incluse) dovrà batterne almeno 10 alla 136, e anche se la scimmia battesse 969 caratteri al minuto, come è riuscito a fare il milanese Carlo Parisi, campione mondiale di velocità di scrittura su tastiera nel 2014 (leggete qui), per digitare così tanti caratteri occorrerebbero comunque 10 alla 127 anni, il che è un tempo incommensurabilmente più lungo dell'età attuale dell'universo, pari a "soli" 10 alla 10 anni. In altre parole, la scimmia digiterà per un tempo molto, molto più lungo di quello che ci separa dal Big Bang senza riuscire a tirar fuori quella celeberrima terzina. Analogamente, potremmo aspettare per un tempo eccezionalmente più lungo dell'età delle galassie senza mai vedere le molecole di gas nei due recipienti A e B del Diavoletto di Maxwell che si ritirano spontaneamente tutte da una parte!

Abbiamo così imparato che una cosa è la possibilità (cioè la realizzabilità), un'altra è la probabilità di un evento. Ad esempio, se io gioco a bridge con tre amici, è possibile che io mi veda servite tutte e 13 le carte di picche, un altro tutte e 13 le carte di cuori, il terzo tutte e 13 le carte di fiori e l'ultimo tutte e 13 le carte di denari? Certo che sì. Ma la probabilità che questa situazione eccezionale si realizzi è tanto bassa, che probabilmente essa non si è mai verificata nell'intera storia dell'uomo. Ciò che io non osservo non è necessariamente impossibile, perché il non osservabile può semplicemente essere troppo raro per poter essere osservato. Collegando perciò l'entropia con la probabilità, si può eliminare sia ogni riferimento ai processi reversibili, dai quali discende la misura dell'entropia, sia ogni riferimento "antropomorfo" nella definizione di tale sfuggente grandezza.

Vogliamo ora dare una veste quantitativa alla definizione probabilistica o, meglio, statistica dell'entropia, fornita in quel che precede. Infatti è naturale, dopo essersi resi conto del fatto che l'entropia è una grandezza statistica. Questa legge sarà l'equazione di Boltzmann.

Ludwig Boltzmann (1844-1906) ebbe infatti il merito di aver sviluppato addirittura una nuova branca della fisica, nota come termodinamica statistica. Delle distribuzioni di Maxwell parleremo più avanti. Per ora, accontentiamoci di notare che ad un solo stato termodinamico, macroscopicamente individuato dalle variabili P, V, T (detto per questo macrostato), può essere fatto corrispondere, a livello microscopico, un grande numero di stati dinamici microscopici a livello molecolare, cioè a diverse disposizioni delle molecole e a diverse distribuzioni di velocità (quelli che abbiamo già chiamato microstati). Infatti, la descrizione classica di uno stato termodinamico richiede solo le tre variabili macroscopiche pressione, volume e termodinamica, e non la determinazione della posizione e della velocità di ogni particella del sistema; in Termodinamica, ormai lo sappiamo, ciò che conta è solo l'effetto globale, prodotto in tanti modi differenti a seconda di come le molecole si dispongono.

Prendiamo per esempio due recipienti comunicanti A e B, come nell'esperienza del Diavoletto di Maxwell. Se un certo numero di molecole è spostato da A a B, ed altrettante da B ad A, l'effetto globale (cioè lo stato termodinamico) palesemente non muta, mentre invece muta lo stato microscopico del sistema. Quando un sistema è in equilibrio termodinamico, in generale non è affatto in equilibrio anche a livello microscopico, e perciò si evolve attraverso tutta una serie di microstati diversi. Data l'impossibilità di conoscere tutti i fattori che regolano l'evoluzione microscopica, giocoforza ci si accontenta, nella Termodinamica statistica, di assumere che la realizzazione in un dato istante di un microstato o di un altro sia un fatto puramente casuale, ed inoltre i microstati con uguale energia totale sono equiprobabili.

Senza quest'ultima ipotesi sarebbe impossibile calcolare qualunque probabilità nel senso classico del termine, così come non si possono calcolare le probabilità con cui si lancia una moneta, se i casi di testa e croce non risultano ugualmente probabili. Detto questo, si può prevedere logicamente che un sistema isolato tende a spostarsi macroscopicamente nel macrostato corrispondente al maggior numero di microstati equiprobabili. Insomma, va là dove la maggior parte dei microstati tende ad andare. Lo stato termodinamico più probabile (e quindi operativamente misurabile) è quello che corrisponde al maggior numero di stati microscopici possibili. Il numero di microstati corrispondenti ad un unico macrostato è chiaramente proporzionale alla probabilità che tale stato macroscopico si realizzi. Tale probabilità prende comunemente il nome di probabilità termodinamica, anche se non è una probabilità nel senso classico di questo termine, perchè non è il rapporto tra il numero dei casi favorevoli e quello dei casi possibili, e risulta invece proporzionale al numero dei microstati che danno vita a quel macrostato. Ecco un'ingegnosa animazione che illustra questo concetto, applicato ad un gas formato da sei molecole e contenuto nei soliti due recipienti comunicanti mediante un orifizio:

Pur essendo alquanto diversa dalla probabilità matematica di Pascal e Fermat, la probabilità termodinamica ne conserva tutte le proprietà, tra cui il:

Teorema della Probabilità Composta: la probabilità di un evento composto da più condizioni tra loro indipendenti è uguale al prodotto delle singole probabilità.

Se per esempio voglio la probabilità che da un mazzo di 40 carte sia estratto il re di denari, la probabilità che ciò avvenga è il prodotto della probabilità che venga estratto un re (4/40 = 1/10) e di quella che venga estratta una carta di denari (10/40 = 1/4); è cioè pari ad 1/40, ed infatti c'è un solo re di denari su 40 carte.

Chiariamo il concetto di probabilità termodinamica facendo ricorso al seguente esempio. Lanciamo un certo numero n di dadi da gioco, e consideriamo macrostati diversi quelli in cui è diverso il punteggio medio conseguito, cioè la somma delle facce divisa per il numero dei dadi. Tale punteggio assume nel nostro esempio il significato di variabile termodinamica, mentre un microstato è rappresentato da una sequenza di punteggi dei singoli dadi. Indichiamo con ( α₁, α₂, ..., α_n ) il microstato rappresentato dal punteggio α₁ del primo dado, dal punteggio α₂ del secondo dado... fino al punteggio α_n dell'n-esimo dado. La variabile termodinamica viene indicata con X ed è contenuta in un intervallo del tipo [ 1 ; 2 ), [ 2 ; 3 ), eccetera. Otteniamo così la seguente tabella, che contiene i microstati corrispondenti ad ogni valore di X, la relativa probabilità termodinamica e le loro somme S, nonché le probabilità matematiche, rappresentate dai rapporti P/S, nel caso in cui abbiamo solo due dadi a disposizione:

X	microstati per n = 2	P	P/S
[ 1 ; 2 )	( 1 , 1 ) ( 2 , 1 ) ( 1 , 2 )	3	1/12 (8,3 %)
[ 2 ; 3 )	( 1 , 3 ) ( 1 , 4 ) ( 2 , 2 ) ( 3 , 2 ) ( 2 , 3 ) ( 4 , 1 ) ( 3 , 1 )	7	7/36 (19,4 %)
[ 3 ; 4 ]	( 1 , 5 ) ( 2 , 4 ) ( 3 , 3 ) ( 4 , 2 ) ( 5 , 1 ) ( 1 , 6 ) ( 2 , 5 ) ( 3 , 4 ) ( 4 , 3 ) ( 5 , 2 ) ( 6 , 1 ) ( 2 , 6 ) ( 3 , 5 ) ( 4 , 4 ) ( 5 , 3 ) ( 6 , 2 )	16	4/9 (44,4 %)
( 4 ; 5 ]	( 3 , 6 ) ( 4 , 5 ) ( 5 , 4 ) ( 6 , 3 ) ( 4 , 6 ) ( 5 , 5 ) ( 6 , 4 )	7	7/36 (19,4 %)
( 5 ; 6 ]	( 5 , 6 ) ( 6 , 6 ) ( 6 , 5 )	3	1/12 (8,3 %)

È facile convincersi che, aumentando il numero dei dadi, la probabilità di ottenere un punteggio contenuto nella fascia centrale, cioè ( 3,5 ± 0,5 ), si va approssimando rapidamente all'unità, cioè alla certezza. Al contrario, la probabilità di trovare valori della variabile termodinamica prossimi a 1 o a 6 tende a zero per valori di n → ∞.

Perciò, con un errore che tende a zero per n → ∞, si può affermare che la variabile termodinamica X da noi costruita assume il valore ( 3,5 ± 0,5 ), perchè questo è il più probabile in ogni caso!

Ora, questo modellizza bene la situazione di un vero sistema termodinamico, in cui il numero delle particelle (i "dadi" della termodinamica) è effettivamente gigantesco, e pertanto i valori assunti dalle variabili termodinamiche sono, all'equilibrio, quelli del macrostato di maggior probabilità termodinamica, all'interno di inevitabili fluttuazioni certamente contenute al di sotto degli errori di misura. Quindi, se il sistema è abbandonato a se stesso, certamente si assesta su quel macrostato!

Noi sappiamo già dal capitolo precedente che tale evoluzione avviene nel senso delle entropie crescenti; ci deve quindi essere un legame tra entropia e probabilità. Vediamo come ci si arriva da un punto di vista strettamente matematico.

Si è detto che per la probabilità termodinamica deve valere il teorema della probabilità composta; deve allora essere possibile individuare una funzione del tipo S = f (P), atta ad esprimere il legame funzionale tra P e l'entropia S, tale che:

Pongo ora P₁ = x e P₂ = x ( 1 + ε ), con ε piccolo a piacere. Allora la precedente diventa:

Ora dobbiamo ricorrere a un concetto tipico dell'Analisi Matematica; chi non ne possiede i suoi strumenti, salti pure alla conclusione. Indichiamo con f '(P) la derivata di f (P). Essendo ε infinitesimo, si avrà:

Se in questa relazione pongo x = 1 (il microstato è costituito da un solo stato possibile), deve risultare:

Questa equazione è valida anche per ε = 0, a patto di porre in essa f (1) = 0. Chiamiamo ora f '(1) = k. Si trova così l'equazione:

Si tratta di un'equazione differenziale a variabili separabili. Separiamole e si ha:

Poiché si è stabilito che f (1) = 0, ne segue necessariamente che C = 0. Ho così la seguente relazione tra l'entropia e la probabilità termodinamica:

Che la relazione fosse di tipo logaritmico, anche al di là di questi ingegnosi passaggi matematici, lo poteva dedurre anche uno studente delle Scuole Medie Superiori. Infatti la funzione S = f (P) deve soddisfare due evidenti proprietà. Anzitutto, al crescere dell'entropia cresce anche la probabilità termodinamica. Infatti, consideriamo per esempio un gas che si diffonde irreversibilmente da un recipiente A a un recipiente B. Chiaramente l'entropia cresce; ma cresce anche la probabilità termodinamica, giacché la probabilità che tutte le molecole si trovino dalla stessa parte della paratia è 1/2^N, come si ricorderà dal paragrafo precedente, dove N è molto grande: 1/2^N vale meno di un milionesimo già se N = 20. La probabilità che le molecole siano ugualmente ripartite tra i due recipienti si approssima all'unità per N molto grande. Quando infatti viene rimosso il vincolo tra A e B, il sistema passa da un macrostato, corrispondente ad un certo numero di microstati, ad un altro macrostato rappresentato da un numero di microstati estremamente più grande del primo. La rimozione del vincolo fornisce cioè alle molecole la possibilità di ridistribuirsi su microstati in precedenza non realizzabili. Dunque, S deve essere una funzione crescente di P.

In secondo luogo, vale la proprietà additiva sopra ricordata; cioè, se ho due sistemi termodinamici caratterizzati dalle entropie S₁ e S₂, l'entropia complessiva del sistema 1 + 2 è pari ad S₁ + S₂, cioè l'entropia è una grandezza estensiva. Ma, se P₁ e P₂ sono le probabilità termodinamiche dei due macrostati, la probabilità che quelle due condizioni si verifichino contemporaneamente è P₁ * P₂. Cioè, alla somma di entropie corrisponde il prodotto della probabilità termodinamica. Ora, l'unica funzione elementare a noi note che trasforma i prodotti in somme è il logaritmo, per via della ben nota proprietà secondo cui:

Resta da determinare, in ogni caso, il valore della costante k nella (7.5). A questo scopo, cerchiamo di far valere quest'ultima relazione in un caso in cui si sa calcolare l'entropia in base alla definizione termodinamica, e contemporaneamente si conosce il numero dei microstati, e quindi la probabilità termodinamica. Tale circostanza si verifica nell'espansione libera del gas perfetto. Supponiamo che un gas contenuto in un recipiente di volume V si espanda liberamente, cioè senza scambi energetici con l'esterno, in un altro recipiente identico, venendo infine ad occupare un volume complessivo 2 V. Usiamo una mole di gas perfetto monoatomico, per il quale si sa che c_V = 3 R / 2 e γ = 5/3. La trasformazione in questione è isoterma; infatti Q = 0, W = 0, quindi ΔU = 0 e ΔT = 0. Allora, per la legge di Boyle si ha P₁ V₁ = P₂ V₂, e di conseguenza si ha che:

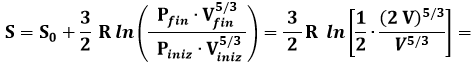
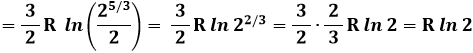
Si è posto S₀ = 0 in base al Terzo Principio della Termodinamica, per cui S = 0 a T = 0 K. Ora, ricordando dal calcolo precedente che un gas in espansione libera formato da un numero N di molecole ha approssimativamente 2^N stati possibili, adoperando un numero di Avogadro N_AV di particelle per la (7.5) si ha:

Quindi k è una costante universale, prende il nome di costante di Boltzmann, la si indica con K_B e vale:

Questa formula è nota come l'equazione di Boltzmann, e grazie ad essa svanisce qualunque influsso antropomorfo sulla definizione di entropia, poiché essa viene universalmente correlata ad una funzione matematica univocamente calcolata. Boltzmann la riteneva così importante, che chiese venisse incisa sulla propria tomba (k indica la costante di Boltzmann e W il numero di microstati, cioè la probabilità termodinamica):

« La geniale intuizione di Boltzmann è stata quella di far corrispondere l'equilibrio macroscopico alla distribuzione energetica realizzata dal massimo numero di configurazioni microscopiche, esprimendo l'entropia in funzione di tale numero. Di conseguenza, egli ha potuto interpretare quantitativamente, e non solo qualitativamente, la seconda legge della termodinamica in termini probabilistici: come una legge, cioè, che afferma la schiacciante prevalenza del passaggio spontaneo da stati meno probabili a stati più probabili (o anche da stati meno «confusi» a stati più «confusi», da stati più «ordinati» a stati più «disordinati» ), fino a raggiungere la distribuzione di equilibrio. » (G. Zanarini, "Entropia, informazione, complessità")

Quanto discusso permette di comprendere un nuovo aspetto, sinora inedito, dei concetti di entropia e di irreversibilità. Per chiarire questo nuovo fatto, introduciamo il cosiddetto principio dell'invarianza temporale. Esso afferma che le leggi di natura rimangono invariate quando al tempo t si sostituisce ( – t ) nelle equazioni del moto. Ciò significa che ogni processo fisico è possibile anche se evolve nell'ordine cronologico opposto. Anche facendo girare la "moviola" all'indietro, insomma, le leggi della Fisica devono risultare concettualmente valide.

Tale legge è verificata praticamente per tutti i sistemi meccanici, per cui tali fenomeni sono simmetrici rispetto all'inversione della linea temporale; in altre parole, sono reversibili. Invece, noi sappiamo che nel complicato mondo macroscopico dei processi termodinamici, ciò non è affatto vero. Eccoci dunque alle prese con un nuovo paradosso. La soluzione sta nel fatto che possibilità non vuol dire probabilità. In altre parole, in linea di principio tutti i processi sono possibili anche invertendo l'ordine dei tempi, ma in pratica esistono enormi differenze, in termini di probabilità, tra un processo ed il suo inverso.

Quando un evento è molto semplice, come per esempio l'urto tra due molecole, il processo diretto e quello inverso rispetto al tempo presentano, in generale, la medesima probabilità. Nel processo dinamico di urto, basta cambiare il segno delle velocità delle due particelle per riportarle nelle condizioni iniziali. Se invece la successione degli eventi risulta estremamente complessa, cioè interessa un numero estremamente grande di molecole e di singoli processi elementari, lo svolgersi spontaneo del fenomeno si manifesta solo nella direzione di massima probabilità, direzione che noi assumiamo come la "vera" direzione del tempo.

Tutto questo comporta una conseguenza inevitabile: l'esistenza e l'ineluttabilità di una freccia del tempo. Se io vedessi un filmato in cui i mille pezzi in cui una zuppiera di porcellana appare frantumata sul pavimento si rianimano per magia e ritornano spontaneamente sul tavolo a ricostituire la zuppiera intera, oppure uno nel quale, come si può vedere nell'animazione qui a sinistra, l'inchiostro scuro sciolto in una bacinella si ritira spontaneamente in una metà di essa, ne concluderei che i filmati sono stati proiettati a rovescio; e la stessa cosa penserei se vedessi un bicchiere di acqua tiepida diventare improvvisamente bollente, con la spontanea formazione in esso di un cubetto di ghiaccio, oppure se assistessi al ringiovanimento di una rana, che ritorna girino e poi uovo. Il motivo di tutti questi fatti è lo stesso per il quale il calore non fluisce "spontaneamente" da un corpo freddo ad uno caldo, e il rendimento di una macchina termica è sempre minore di uno. Queste situazioni sono esempi che mostrano come il mondo corra automaticamente nella direzione della massima probabilità termodinamica; questa è la spontanea direzione in cui evolve ogni fenomeno chimico e fisico, e quindi è la spontanea direzione del tempo. In altre parole, la "freccia del tempo" non è altro che la direzione di massima probabilità. Il tempo scorre nella direzione in cui la probabilità è maggiore, e questo spiega l'unidirezionalità dei processi termodinamici. Non è che sia impossibile viaggiare all'indietro nel tempo: solamente, è altamente improbabile riuscirci. Tutto ciò mette la pietra tombale su ogni speranza di poter costruire una macchina del tempo, come si è già anticipato nel § 5.1.

A questo punto, è possibile dire che vi è un legame diretto tra l'entropia e l'ordine. Infatti, quando un sistema è strutturato secondo una configurazione coerente, costruita su un principio logico che ci permette di distinguere una proprietà costante, si parla di ordine. L'ordine implica la disposizione razionale ed armonica di alcuni elementi nello spazio e nel tempo, secondo esigenze pratiche e ideali, o secondo norme dettate da una legge matematica. Questo è il caso dei cristalli, come quello cubico di cloruro di sodio (NaCl) illustrato qui sotto:

La sua struttura regolare è dovuta alla ripetizione di un singolo cubetto elementare nelle tre direzioni dello spazio. Nulla di più ordinato possiamo pensare di un cristallo, perchè i singoli atomi possono muoversi di pochissimo, vibrando intorno alla loro posizione di equilibrio nel cristallo. Un gas ad alta temperatura, invece, è quanto di più disordinato si possa concepire, con atomi o molecole caoticamente distribuiti alla rinfusa.

Ora, tutti i processi naturali tendono ad evolvere verso stati in cui il disordine è sempre maggiore, come si può osservare nel caso di un cubetto di canfora che, se esposto all'aria, sublima, aumentando il proprio disordine. Mentre è facile passare da una condizione di ordine ad una di disordine, il passaggio inverso non avviene MAI spontaneamente.

Supponiamo ad esempio di avere un mazzo di carte nuove, distribuite in bell'ordine su un tavolo secondo i semi e secondo il colore. Se rimescolo questo mazzo, qualunque traccia di ordine sparisce, ed è estremamente improbabile che si riesca a ripristinare nuovamente l'ordine iniziale, anche continuando a rimescolare a caso per giorni, mesi, anni e secoli. Infatti, se il mazzo contiene 40 carte, come nella foto qui sotto, secondo il calcolo combinatorio le permutazioni possibili delle carte da gioco sono 40! (40 fattoriale), cioè circa 8,16 x 10⁴⁷, e quindi vi è solo una probabilità su 816 miliardi di miliardi di miliardi di miliardi di miliardi, di ripristinare l'ordine iniziale. Troppo, perchè la natura ne possa tenere conto. Ammettendo di impiegare 10 secondi a rimescolare il mazzo ogni volta, il tempo necessario a provare tutte le combinazioni possibili sarebbe dell'ordine dei 10⁴¹ anni, e quindi enormemente più lungo dell'età stessa dell'universo. Ci troviamo nella stessa situazione descritta nel § 7.2 della scimmia che cerca di comporre la prima terzina della Divina Commedia battendo a caso i tasti di un computer!

Applichiamo la (7.6) al mazzo di 40 carte della figura soprastante. L'entropia di questo mazzo è pari a:

S = K_B ln (40!) = 1,38 x 10^–23 x ln ( 8,16 x 10⁴⁷ ) = 1,52 x 10^–21 J K^–1

Analogamente, per passare ad un esempio un po' più fisico, se riempio un recipiente per metà di zucchero e per metà di sale, lo chiudo e lo agito, io passo spontaneamente da uno molto ordinato ad uno altamente disordinato, ma il viceversa non avverrà mai spontaneamente, ripristinando l'ordine iniziale, neanche se io continuassi ad agitare per tutta la vita. Anche in questo caso, infatti, la configurazione rappresentata da zucchero tutto stratificato sotto e sale tutto stratificato sopra è unica, mentre quelle in cui i granelli sono rimescolati a caso è rappresentata da un numero incredibilmente grande di configurazioni microscopiche, e quindi è più probabile. Anche quando si parla di ordine e disordine, dunque, il sistema è di natura probabilistica, e dunque fa capolino inevitabilmente il concetto di entropia.

Naturalmente, se si opera su tempi scala davvero lunghi, anche configurazioni parzialmente o totalmente ordinate possono saltare fuori dal cappello a cilindro, se è vero che la storia dei giochi d'azzardo annovera dei colpi di fortuna davvero strabilianti. Ad esempio, come riporta questo articolo, il 26 ottobre 2016 presso una tabaccheria di Vibo Valentia un anonimo giocatore ha centrato un "sei" al Superenalotto che gli ha fruttato la vincita di ben 163.538.706 euro a fronte di una spesa per la schedina di soli tre euro! Eppure, la probabilità di centrare un "sei" al Supernalotto è pari appena a:

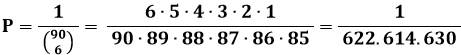
Siccome ogni settimana migliaia, anzi milioni di persone giocano al Superenalotto, dopo un numero di giocate alto ma non astronomico, e quindi dopo un tempo decisamente inferiore non solo alla vita dell'universo, ma anche alla vita media dell'uomo, la combinazione vincente viene azzeccata. In genere, però, per realizzare combinazioni ordinate con i sistemi termodinamici è necessario lavorare su tempi scala molto più lunghi, se è vero che 2 elevato al Numero di Avogadro è un numero con 10 alla 22 cifre!! Se al Superenalotto si estraessero non sei numeri su 90 ma su un Numero di Avogadro, la probabilità di azzeccarle tutte sarebbe così bassa, da risultate tecnicamente uguale a zero, ed una cosa del genere non sarebbe mai accaduto non solo a memoria d'uomo, ma di dinosauro. In tal caso, ricordando le proprietà dei logaritmi, l'entropia di questo iper-mazzo di carte diverrebbe:

Abbiamo così compreso che la distribuzione più probabile delle molecole, compatibilmente con lo stato del sistema, è quella più disordinata, perchè è quella che si può realizzare nel maggior numero di modi. Ogni deviazione da queste condizioni è altamente improbabile o, perlomeno, comporta l'intervento di un essere senziente tipo il Diavoletto di Maxwell per essere realizzata.

Naturalmente, la transizione costante dall'ordine al disordine è quotidianamente sotto i nostri occhi anche in Termodinamica. Infatti, quando il lavoro si trasforma in calore, si ha il passaggio da un movimento relativamente ordinato delle molecole (per esempio spinte da uno stantuffo dentro un cilindro) ad uno fortemente disordinato, Se si potessero osservare le molecole di un gas che si agitano durante una cessione di calore, si potrebbe vederle sbatacchiare qua e là nel movimento più caotico del mondo. Il calore insomma è la più disordinata tra le forme di energia.

La stessa cosa si verifica quando il calore passa da un corpo più caldo ad uno più freddo. Infatti, inizialmente è facile distinguere i due corpi, avendo temperature differenti, mentre, una volta raggiunto l'equilibrio, è cresciuto il disordine, essendo diminuita la possibilità di distinguere le singole parti del sistema.

Idem dicasi per un solido che fonde: la struttura del solido è ordinata, essendo di tipo cristallino (i solidi amorfi come il vetro e il polistirolo vengono chiamati "falsi solidi"!), ma quando subisce una fusione gli atomi si disordinano completamente, e quindi il disordine cresce. Tutti i fenomeni irreversibili fanno aumentare il numero dei modi in cui un particolare macrostato può realizzarsi. In altre parole, fanno aumentare la probabilità termodinamica, e quindi l'entropia.

Ne consegue che l'entropia di un sistema rappresenta una misura del grado di disordine molecolare che regna nel sistema. Abbiamo finalmente compreso qual è la natura dell'irreversibilità e del verso naturale associato agli eventi. Esso proviene semplicemente dall'ordine che si trasforma in disordine! Possiamo insomma formulare il:

SECONDO PRINCIPIO DELLA TERMODINAMICA, ENUNCIATO DEL DISORDINE: le uniche trasformazioni reali sono quelle che massimizzano il disordine dei sistemi termodinamici.

Nel lontano passato, il nostro universo doveva essere molto più ordinato di quanto non lo sia oggi. Infatti, nel Big Bang tutto era concentrato in un "uovo cosmico" (Hiranyagarbha, come direbbero i testi indù Bhagavad Gita), di dimensioni microscopiche, che poi si è "schiuso", generando tutto il cosmo quale oggi lo vediamo. In futuro, al contrario, sarà molto più disordinato di quanto non lo sia oggi, e al limite arriverà in uno stato disordinatissimo, in cui tutte le temperature risulteranno uniformi. Questo è lo stato di "morte termodinamica" del quale abbiamo discusso in precedenza, e che ha angosciato le notti di Pascoli e di Lovecraft.

Ora, siccome quando il disordine è massimo lo è anche l'entropia, si può pensare che il sistema cessi di evolvere la massima uniformità. Se poi consideriamo il complesso rappresentato dall'unione tra un sistema termodinamico e il suo ambiente circostante, anch'esso sarà caratterizzato da un continuo aumento dell'entropia, cioè del disordine. Quando l'entropia avrà raggiunto il suo massimo, certamente non si avranno più differenze di temperatura, e quindi tutta l'energia dell'universo, per quanto enorme sia, non potrà mai più essere utilizzata. Quando l'universo avrà raggiunto la massima entropia (la perfetta diluizione della materia e dell'energia nello spazio e nel tempo), esso dovrebbe trovarsi in equilibrio assoluto. In tale tutt'altro che simpatica situazione sarebbe impossibile realizzare qualunque processo chimico, fisico e biologico. Sarebbe la morte definitiva dell'universo. Da questo momento in poi non cambierà più nulla, e sarà come se il tempo abbia cessato di scorrere. Sarà allora calato l'ultimo sipario sulla vita, e si realizzerà in tal modo la terrificante eventualità prospettata dal grande scrittore americano Edgar Allan Poe (1809-1849) nel suo allucinante racconto intitolato « La Maschera della Morte Rossa »:

« E allora tutti compresero e riconobbero la presenza della "Morte Rossa". Era giunta come un ladro nella notte, ad uno ad uno i gaudenti giacquero nelle sale irrorate di sangue delle loro gozzoviglie, e ciascuno morì nell'atteggiamento disperato in cui era caduto. E quando l'ultimo morì, anche l'orologio d'ebano tacque, e le fiamme dei tripodi si spensero. E il Buio, la Putrefazione e la Morte Rossa dominarono indisturbati su tutto. »

Questa macabra conclusione a cui giunse Clausius nel 1867, ragionando intorno al concetto di entropia, ha ispirato persino un albo del celebre fumetto "Dylan Dog", e precisamente il n° 126 del marzo 1997, come si vede qui sopra. A questo punto però mi sembra giusto squarciare questa cupa atmosfera di pessimismo, e presentare anche il rovescio della medaglia. Infatti anche noi uomini, dopotutto, siamo delle macchine termodinamiche che trasformano l'ordine in disordine. Ma attenzione all'equazione fondamentale: vita equivale ad ordine, e non vita a disordine. La nostra esistenza stessa dipende dal funzionamento di tutta una serie di processi fisici e chimici perfettamente bilanciati tra di loro, e la stessa catena del DNA, che miliardi di anni fa diede inizio alla vita così come oggi la intendiamo, è una delle più regolari strutture molecolari che la chimica organica conosca. Quando un organismo muore, si raffredda, e va in equilibrio termodinamico con l'ambiente, per via della cessazione dei processi biologici che lo mantenevano in vita. La morte è il destino naturale di tutte le creature viventi, e « noi viviamo su un pianeta sul quale l'istituto della grazia è sconosciuto », come ebbe a dire lo scrittore Vittorio Messori. La morte è ineluttabile perchè lo è il Secondo Principio della Termodinamica nell'enunciato del disordine, da noi appena formulato.

Tuttavia noi sappiamo che, almeno una volta nella storia dell'universo, la "freccia del tempo" si è invertita: quando la vita è nata. In quel caso, infatti, si è passati dal disordine della non vita all'ordine delle macromolecole complesse e dei sistemi biologici viventi. Come ciò ha potuto accadere? Se ci basiamo unicamente sul Secondo Principio, bisogna concludere che la probabilità di un evento del genere era talmente bassa, che sarebbe occorso un tempo di trilioni e trilioni di anni, affinché avesse avuto modo di realizzarsi. Eppure, si è verificato "appena" 10 miliardi di anni dopo il Big Bang, ammesso che non si fosse già verificato su altri mondi prima che sulla Terra, come fa sospettare la continua scoperta di pianeti extrasolari, molti dei quali assomigliano molto alla Terra e sembrano in grado di ospitare la vita (si pensi alla scoperta dei sette pianeti in orbita attorno alla stella Trappist One, posta a 39,5 anni luce da noi nella costellazione dell'Acquario, annunciata il 22 febbraio 2017). Il famoso scienziato dello Sri Lanka Nalin Chandra Wickramasinghe (1969-) ha dichiarato che « un vento di tempesta che soffiasse su delle carcasse di aereo avrebbe più probabilità di ricostruire da solo un aviogetto perfettamente funzionante, di quante non ce ne sarebbero di creare la vita mettendo insieme a caso gli elementi che la compongono »!

Come si spiega tutto questo? I casi sono tre. O l'evento è meno improbabile di quanto si pensi, ma allora tutto il cosmo pullulerebbe di vita e la Galassia sarebbe affollata come un supermarket di specie intelligenti, così come mostrano le grandi saghe di Star Trek e Star Wars. Oppure, noi abbiamo avuto una fortuna sfacciata come il vincitore di 163 milioni e mezzo di euro al Supernalotto cui si è accennato sopra, ma i colpi di fortuna, si sa, sono sempre piuttosto improbabili. Oppure, esiste davvero un Deus ex Machina e noi siamo davvero il prodotto di un Disegno Intelligente. Effettivamente anche scienziati nel vero senso della parola si sono spinti ad affermare un intervento soprannaturale all'origine della vita; ma questa questione esula dagli intenti del presente ipertesto, ed io non prenderò posizione in questo dibattito, onde lasciare a tutti la possibilità di prendere posizione su questo argomento, come gli detta la sua sensibilità. Pensando alla vastità dell'universo e al mistero che circonda l'origine della vita e dell'intelligenza umana, comunque, non possono non venire in mente gli splendidi versi di Charles Baudelaire (1821-1867):

"Par dela le soleil, par dela les ethers,
par dela les confins des spheres etoilees,
mon esprit, tu te meus avec agilite,...
avec un indicible et male volupte"

[Al di là del Sole, al di là dell'etere,
al di là dei confini delle sfere stellate,
tu, mio spirito, ti muovi con scioltezza...
con indocile e maschia voluttà]
("Elevation", da "Le Fleurs du Mal")

Chi scrive non si illude di aver resa simpatica l'entropia a chi legge; tuttavia, comprenderne il significato è basilare, poiché essa continua a spuntare fuori in innumerevoli campi delle scienze. Infatti, poiché qualunque sistema complesso è suscettibile di una trattazione statistica, essa si ritrova nello studio delle proprietà della materia condensata, con applicazioni alla Fisica dei Materiali, ma anche nello studio degli equilibri chimici. La si ritrova addirittura nello studio delle mutazioni genetiche e in quello della trasmissione dei messaggi. Infatti un messaggio scritto è pur sempre una successione di simboli, in cui un disturbo di trasmissione può provocare qualche disordine casuale, misurabile per mezzo di una variabile per molti aspetti simili all'entropia. Approfondiamo in particolare questo concetto.

Nel 1949 Claude Elwood Shannon (1916-2001) e Warren Weawer (1894-1978), studiosi di teoria della comunicazione, proposero una misura quantitativa dell'informazione tramite la funzione H che codificava questa misura, detta entropia informazionale, e che coincide con la formula dell'entropia di un sistema fisico discreto. Ecco la formula elaborata dai due matematici:

Facciamo un esempio notevole di entropia informazionale. Consideriamo la seguente, curiosa riproduzione del volto del Presidente americano Barack Obama, tratta da questo sito:

Essa è in realtà un mosaico di ben 2250 tessere realizzate con 200 diverse immagini di precedenti Presidenti USA. Questa immagine-mosaico rende intuitivo il fatto the l'informazione relativa al volto di Obama, cioè il suo riconoscimento, dipende dal numero e dalla varietà di simboli (le diverse tessere) che codificano il messaggio. Una valutazione della quantità di informazione associata all'immagine e data, in prima approssimazione, proprio dall'entropia informazionale:

dove

(k = 1, 2, 3, ..., 200) indica la frequenza con la quale la k-esima faccia di Presidente si ripresenta nel mosaico.

Per fare un esempio, una conversazione con una persona che può dire sempre e solo una cosa, come il personaggio di Hodor nella serie televisiva "Game of Thrones", che dice solo "Hodor", sarebbe prevedibile ma con poca informazione. Una chiacchierata con Pikachu sarebbe un po' meglio; il famoso Pokémon può pronunciare solo le sillabe del suo nome, ma può riorganizzarle, a differenza di Hodor. Allo stesso modo, un testo che contiene una sola lettera dell'alfabeto o un brano musicale con una sola nota sarebbe relativamente facile per il cervello da imparare o da riprodurre, ma il brano faticherebbe a trasmettere qualsiasi tipo di messaggio.

La sorprendente analogia tra termodinamica e teoria delle comunicazioni aprì la strada per interessanti successivi approfondimenti. Léon Brillouin (1899-1969), nel suo famoso libro "Science and Information Theory", del 1960, affermò che esiste una precisa relazione tra la variazione dell'entropia di un sistema e l'acquisizione di informazioni relative al sistema stesso. Poiché la formula di Shannon e la formula dell'entropia hanno la stessa espressione (a parte il coefficiente moltiplicativo), si può dunque interpretare l'entropia come mancanza di informazione sul sistema considerato.

« L'entropia è considerata in generale come espressione del disordine di un sistema fisico. Più precisamente, si può dire che l'entropia misura la mancanza di informazione sulla strutture effettiva del sistema. Questa mancanza di informazione implica la possibilità di una grande varietà di strutture microscopiche diverse che sono, in pratica, impossibili da distinguere le une dalle altre. Poiché una qualunque di queste strutture può esistere realmente a un istante dato, la mancanza di informazione corrisponde ad un disordine reale. […] L'entropia è una misura della mancanza di informazione dettagliata relativamente a un sistema fisico: più grande è l'informazione, più piccola sarà l'entropia. L'informazione rappresenta un termine negativo nell'entropia di un sistema, sicché si può definire l'informazione come entropia negativa. »

È quindi possibile diminuire l'entropia di un sistema aumentando l'informazione su di esso, tramite misure più dettagliate della sua configurazione, e l'informazione può così cambiarsi in entropia negativa o "neg-entropia". A sua volta però, come già aveva puntualizzato Szilard, l'informazione può ottenersi soltanto a spese dell'entropia negativa di qualche sistema fisico, ed è quindi impossibile per questa via giungere ad una violazione del Secondo Principio della Termodinamica.

Va sottolineata l'impresa di Suman Kulkarni, ricercatrice dell'Università della Pennsylvania, la quale ha analizzato l'entropia informazionale contenuta in nientemeno che 337 composizioni di Johann Sebastian Bach (1685-1750), trasformando le partiture ini reti di punti, chiamati nodi, collegati da linee, chiamate bordi, e quantificando le informazioni da esse trasmesse. In queste reti, ogni nota della partitura originale è un nodo e ogni transizione tra le note è un bordo. Per esempio, se un brano includeva un Mi seguito da un Do e da un Sol suonati insieme, il nodo che rappresenta il Mi sarebbe stato collegato ai nodi che rappresentano il Do e il Sol. Kulkarni ha scoperto così una variazione nella struttura e nel contenuto informativo dei numerosi stili compositivi di Bach: le corali, un tipo di inno destinato a essere cantato, hanno prodotto reti relativamente scarse di informazioni, anche se più ricche di informazioni rispetto alle reti generate casualmente della stessa dimensione. Le toccate e i preludi, stili musicali spesso scritti per strumenti a tastiera come l'organo, il clavicembalo e il pianoforte, presentano un'entropia informativa più elevata. Naturalmente non è ancora esattamente chiaro come gli schemi di rete identificati dalla Kulkarni si traducano nell'esperienza vissuta dell'ascolto di un brano di Bach: la risoluzione di questo problema spetta alla psicologia musicale, non alla teoria dell'informazione.