![]()
|
"La statistica è l’unica scienza che permette a esperti diversi, usando gli stessi numeri, di trarne diverse conclusioni." Evan Esar (1899-1995) |
.
8.1 Variabili discrete e continue
Anche a distanza di molti anni dalla sua prima formulazione, la teoria cinetica dei gas rappresenta una delle teorie di maggior eleganza e di maggior successo, essendo riuscita a saldare per la prima volta argomenti teorici ed applicazioni pratiche a prima vista diversissimi tra di loro. Oggi l'esistenza degli atomi è universalmente accettata, anche se ancora all'inizio del ventesimo secolo si guardava con diffidenza alla teoria atomica; uno dei grandi meriti della teoria cinetica dei gas è stato proprio quello di anticipare i tempi, avendo precorso gli esperimenti di elettromagnetismo e di fisica nucleare, garantendo prove decisive a favore dell'esistenza delle invisibili molecole.
D'altro canto, le definizioni puramente operative della Termodinamica classica (quelle di cui ci siamo occupati finora), benché di per sé sufficienti ad istituire una serie di relazioni quantitative per esprimere il comportamento dei fluidi termodinamici, delle quali possiamo servirci per le nostre applicazioni pratiche, tuttavia non soddisfano la necessità di darci ragione del comportamento dei sistemi a livello microscopico. Si potrà affermare che si tratta di una necessità puramente intellettuale, ma quanti di noi fin da bambini non si sono accontentati di giocare con un balocco elettronico, ma lo hanno rotto per vederne il meccanismo interno?
Oltre a tutto ciò, la fisica cinetica ci offre l'occasione di vedere come una teoria si sviluppa praticamente dal niente, a cominciare dall'elaborazione di un modello, fino alla deduzione logica delle sue proprietà ed al confronto tra dati sperimentali e risultati teorici. Eppure, alla base di tutto ciò non sono richieste che conosce elementari di dinamica del punto materiale e di statistica. A questo proposito, cominciamo proprio con il presentare alcune nozioni di statistica che ci serviranno per la discussione successiva. In questo contesto occorrerà far uso
Una variabile statistica X è una variabile qualsiasi definita per ogni individuo di un certo insieme, che può assumere valori x diversi da individuo ad individuo. Tale variabile può essere discreta, cioè numerabile, come lo è per esempio il punteggio ottenuto lanciando un dado, oppure continua, ad esempio come l'altezza degli abitanti di una certa città. Nel caso di variabile discreta, dal punto di vista statistico essa è considerata nota quando si conoscono tutti i valori assunti da X ed il numero ni di volte in cui è stato registrato ogni valore xi.
Def. 8.1: Dicesi frequenza del valore xi di una variabile discreta il rapporto tra il numero degli eventi che hanno sortito il valore ed il numero totale degli individui di quella popolazione:
![]()
Def. 8.2: Dicesi momento di ordine p della variabile statistica discreta X, con p numero intero, la quantità:
I momenti in Fisica Statistica si indicano normalmente con < xp >. In particolare, se p = 1 si ha il momento di ordine uno, detto anche valor medio della distribuzione discreta di probabilità:
Il momento di ordine due è la media dei quadrati della variabile discreta x:
Def. 8.3: Dicesi varianza la differenza tra il quadrato della media e la media dei quadrati:
V(x) = < x >2 – < x2 >
Def. 8.4: Dicesi scarto quadratico medio σ la radice quadrata della varianza.
Def. 8.5: Dicesi moda il valore della x per cui fi è massimo. Esso è ovviamente il valore che si riscontra con più frequenza quando si effettua l'indagine statistica (infatti un capo di abbigliamento è "di moda" quando lo indossa la maggior parte della gente).
Invece, nel caso di una variabile statistica continua, è impossibile assegnare un significato al numero di volte in cui si presenta un certo valore x, giacché tale numero è certamente infinito, essendo compreso in un intervallo continuo di valori. Tuttavia, è possibile definire il concetto di "densità di presenza", a patto di far uso in maniera pesante degli strumenti dell'Analisi Matematica; chi non li possiede, salti al termine di questo paragrafo. Intuitivamente, la "presenza" è il numero di volte in cui la variabile assume un certo valore compreso all'interno di un prefissato intervallo, del tipo [ x0 ; x0 + Δx ]. Se n è una variabile anch'essa continua, il che è lecito se la N è molto, molto grande, ed osservando che n tende a zero al tendere a zero di Δx, si può enunciare la:
Def. 8.6: Dicesi densità di presenza il limite per Δx → 0 del numero di presenze della variabile continua tra x0 e x0 + Δx:
![]()
Conoscendo la densità di presenza, si può calcolare quante volte X assume valori compresi tra limiti scelti a piacere, per esempio tra x1 e x2. Infatti, avendosi:
![]()
basterà integrare tra x1 e x2 per ottenere:
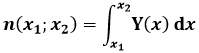
Y(x) può essere una densità di presenza se vale quella che si chiama la condizione di normalizzazione:
![]()
Def. 8.7: Dicesi densità di frequenza di una variabile continua il rapporto tra la densità di presenza e la probabilità totale:
Anche in questo caso deve valere la condizione di normalizzazione:
![]()
Def. 8.8: Dicesi momento di ordine p della variabile statistica continua X, con p numero intero, la quantità:
In particolare, se p = 1 si ha il momento di ordine uno, detto anche in questo caso valor medio della distribuzione continua di probabilità:
![]()
Il momento di ordine due è la media dei quadrati della variabile x:
La definizione di varianza V(x) = < x >2 – < x2 > e di scarto quadratico medio σ è la stessa già introdotta per le variabili discrete, mentre la moda è il valore per cui la y(x) è massima.

|
L’anfora campaniforme a figure nere di Exechias conservata ai Musei Vaticani è tra le ceramiche più famose del mondo antico. Risale al 540-530 a.C. ed è stata rinvenuta in una tomba etrusca a Vulci. Su di essa sono raffigurati Achille e Aiace che, in una pausa dei combattimenti sotto le mura di Troia, giocano a dadi |
Def. 8.9: Dicesi probabilità di un evento il limite a cui tende la frequenza di questo evento allorché il numero delle prove tende all'infinito. Si tratta di una definizione piuttosto diversa da quella classica di Fermat e Pascal cui abbiamo accennato nel capitolo precedente, ma è quella che si adatta meglio ai calcoli statistici. Se l'evento in questione consiste o meno nella comparsa di un valore x nella misura di una variabile X, si ha a che fare con una variabile probabilistica. Essa si considera nota quando sono note tutte le probabilità pi di ogni valore xi nel caso discreto, oppure tutta quanta la distribuzione y(x) in quello continuo. In tal caso, y(x) diventa una distribuzione di probabilità, definita come il rapporto tra la probabilità che X assuma un valore compreso nell'intervallo [ x0 ; x0 + Δx ] e l'ampiezza dell'intervallo stesso, allorché quest'ultima tende a zero:
![]()
Esiste dunque una strettissima correlazione formale tra variabili statistiche e probabilistiche; a queste si possono perciò estendere in modo naturale le definizioni di momenti, media, varianza, moda, eccetera. Vediamo ora un esempio di variabile probabilistica che ha un significato importantissimo anche in Fisica, e non solo nella ricerca demoscopica.
.
8.2 La distribuzione gaussiana
Proviamo ad estrarre a caso 150 cognomi dall'elenco telefonico della provincia di Varese, e a contare le lettere del loro cognome. Introduciamo perciò la variabile probabilistica « numero di lettere del cognome » rappresentata da xi; ni è il numero dei cognomi di lunghezza xi, ed fi è la corrispondente frequenza. Si tratta ovviamente di una variabile discreta, essendo numerabile il numero degli abbonati al telefono. Abbiamo ad esempio la seguente tabella:
|
xi |
ni |
fi |
|
3 |
1 |
0,007 |
|
4 |
3 |
0,020 |
|
5 |
20 |
0,133 |
|
6 |
35 |
0,233 |
|
7 |
33 |
0,220 |
|
8 |
25 |
0,167 |
|
9 |
18 |
0,120 |
|
10 |
11 |
0,073 |
|
11 |
4 |
0,027 |
|
|
N = 150 |
1 |
I dati così ottenuti possono essere riportati in un istogramma, simile a quello qui sotto riportato, che ci dà l'idea di come si realizza la distribuzione:

La moda è manifestamente 6, perchè il 23 % dei cognomi sortiti è composto da sei lettere. E la media? Utilizzando la (8.2), basta effettuare il calcolo seguente:

![]()
Dunque, il numero medio di lettere dei cognomi conteggiati è poco più di 7. Il fatto che sia un numero decimale ci dice che non rappresenta un valore reale, ma solo una media. Per la (8.3) si ha poi:
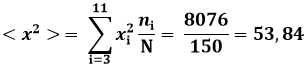
Allora la varianza vale V(x) = < x >2 – < x2 > = 2,765, e lo scarto quadratico medio è pari alla sua radice quadrata, cioè ad 1,663.
Osserviamo che questa distribuzione di probabilità è approssimabile con quella che i matematici chiamano la distribuzione normale o di Gauss, ideata dal tedesco Johann Friedrich Carl Gauss (1777-1855), uno dei maggiori matematici e fisici di tutti i tempi:
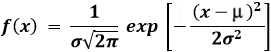
dove μ è il valor medio < x > e σ lo scarto quadratico medio. Nel nostro caso, la funzione sarebbe:
![]()
Ecco la tabella dei valori ottenuti con tale funzione:
| xi | fi vero | f(x) calcolato | errore |
| 3 | 0,007 | 0,011 | 34 % |
| 4 | 0,020 | 0,040 | 100 % |
| 5 | 0,133 | 0,104 | 22 % |
| 6 | 0,233 | 0,189 | 19 % |
| 7 | 0,220 | 0,239 | 9 % |
| 8 | 0,167 | 0,210 | 26 % |
| 9 | 0,120 | 0,129 | 7,5 % |
| 10 | 0,073 | 0,055 | 24 % |
| 11 | 0,027 | 0,016 | 69 % |
L'approssimazione è abbastanza buona per i valori intorno al valor medio. Tale curva permette (almeno approssimativamente) di ricavare la probabilità di trovare un cognome di x lettere, estraendo a casa un nominativo qualunque. Infatti, per la (1) e la (2), allorché si passa dal discreto al continuo, l'area sottesa dalla distribuzione di probabilità rappresenta la probabilità di trovare un valore di x compreso tra due valori prefissati. Non a caso, la probabilità di trovare x compreso tra – ∞ e + ∞ (tutti i valori possibili) è uno, cioè la certezza! Se, ad esempio, voglio trovare la probabilità di avere un cognome di 7 o più lettere, basta sommare i relativi valori di fi:
![]()
= 0,220 + 0,167 + 0,120 + 0,073 + 0,027 = 0,607
e quindi è del 60 %. Si osservi come sia più probabile trovare cognomi di lunghezza media, che cognomi molto lunghi o molto corti. Questo è il significato principale della distribuzione gaussiana, che regola la maggior parte dei fenomeni naturali. Ed ecco l'aspetto della distribuzione gaussiana per diversi valori di μ e di σ:
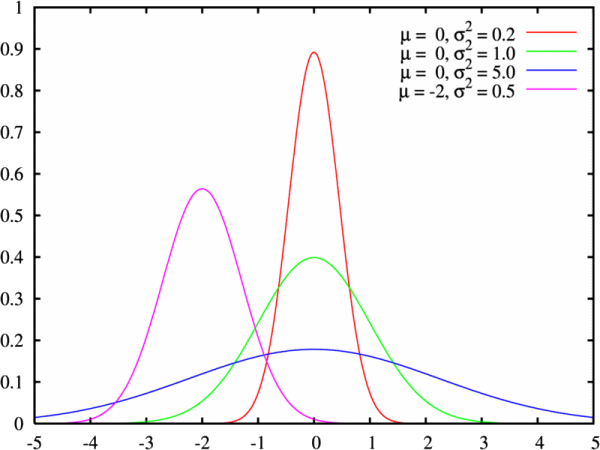
.
8.3 Dal moto browniano alla fisica statistica
Come è possibile applicare queste nozioni alla Fisica, e in particolare alla Termodinamica? La prima osservazione di un fenomeno che in qualche modo collega la Termodinamica classica all'esistenza di una popolazione costituita da un numero enorme di particelle all'interno di un gas fu compiuta nel 1827 dal botanico britannico Robert Brown (1773-1858), il quale osservò con un rudimentale microscopio le particelle di polline in una sospensione acquosa, e si accorse che esse non restavano ferme, ma erano animate da un moto disordinato e continuo, come nella figura sottostante:

Inizialmente Brown attribuì questo moto a qualche misteriosa attività vitale della materia, ovvero ad una proprietà di non meglio specificati "germi di vita". In seguito però egli abbandonò tale ipotesi, essendosi accorto che la stessa proprietà era manifestata dal polline anche dopo prolungata bollitura, o da polvere di composti minerali che sicuramente nulla avevano in comune con la materia vivente.
Fu Albert Einstein (1879-1955), nel 1905 (e quindi un secolo dopo le ricerche di Robert Brown), ad interpretare correttamente il cosiddetto moto browniano, e lo fece con uno dei tre articoli pubblicati durante il suo "annus mirabilis". L'articolo in questione è « Über die von der molekularkinetischen Theorie der Bewegung von Wärme geforderte in ruhenden suspendierten Flüssigkeiten Teilchen » (« Sulla teoria cinetico-molecolare del movimento dovuto al calore di particelle sospese in liquidi a riposo »); gli altri due articoli riguardano rispettivamente la Relatività Ristretta e l'Effetto Fotoelettrico. In tale lavoro Einstein interpretò il moto browniano come una conseguenza degli urti contro le particelle in sospensione da parte delle molecole d'acqua. Il moto browniano rappresentava cioè la prima prova sperimentale diretta dell'esistenza del moto molecolare.
Fu proprio questa constatazione che inserì definitivamente nell'agone della Fisica l'esistenza degli atomi e delle molecole, teorizzata ai primi dell'ottocento dai chimici John Dalton (1766-1844) e Joseph Louis Proust (1754-1826) per interpretare a livello microscopico la cosiddetta legge delle proporzioni multiple, secondo la quale i rapporti tra le diverse masse di un elemento che si combinano con una stessa massa di un altro elemento sono espresse da numeri interi e normalmente piccoli. Se però fino a quel punto non si poteva far altro che postulare la natura discontinua della materia (cioè la quantizzazione della materia) a livello microscopico, non si sapeva ancora come sfruttare la loro esistenza per rendere ragione del comportamento dei corpi macroscopici.
Chi riuscì in questa impresa fu il già citato Ludwig Boltzmann, ai suoi tempi molto contestato dalla comunità dei Fisici e dei Chimici, ponendo le basi della cinetica molecolare, che venne poi magistralmente sviluppata da James Clerk Maxwell, grazie alla prima formulazione statistica della Termodinamica. Purtroppo, ai suoi tempi furoreggiava una concezione fenomenologica secondo cui la realtà fisica era valutabile solo sulla base di ciò che è osservabile, e quindi non poteva fare ricorso a ciò che osservabile non era, come gli atomi e le molecole. Boltzmann non fu in grado di sostenere le sue teorie dal punto di vista sperimentale, fu snobbato dai suoi colleghi, e per questo si suicidò a Duino, località balneare presso Trieste, il 5 settembre 1906, mentre la sua famiglia si trovava in spiaggia (il famoso Erwin Schrödinger ammise che il più grande rimpianto della sua vita era quello di non aver fatto in tempo ad assistere alle sue lezioni). Per ironia della sorte, solo sei anni più tardi Niels Bohr riuscì ad interpretare gli spettri degli elementi chimici sulla base della teoria atomica quantistica da lui stesso formulata. Senza di lui, tuttavia, l'intera storia della Fisica sarebbe stata ben diversa.
Per poter impostare la Teoria Cinetica dei Gas, occorre prima ricordare il modello molecolare dei gas perfetti, da noi delineato nel § 3.1. Il gas è considerato come un insieme di N molecole, dove N è un numero talmente grande da poter essere ritenuto tendente all'infinito agli effetti pratici del calcolo numerico. Le molecole a loro volta sono considerate piccolissime sfere impenetrabili, indeformabili e di volume trascurabile rispetto a quelle del recipiente che le contiene, cioè puntiformi. Nell'intervallo di temperature e di pressioni da noi considerato, la distanza fra le molecole è molto grande rispetto alle dimensioni effettive delle molecole, e tra molecola e molecola c'è il vuoto. Le molecole si trovano in un continuo moto disordinato, detto caos molecolare, e tutte le direzioni del moto sono equiprobabili; in altre parole, le velocità delle molecole sono distribuite in modo isotropo. Le interazioni delle molecole tra di loro e con le pareti che delimitano il volume a disposizione sono unicamente urti elastici, per cui la somma di tutte le energie cinetiche delle molecole è costante nel tempo. Non vi sono interazioni tra le molecole oltre agli urti, per cui, tra un urto e l'altro, il moto delle molecole è rettilineo uniforme. Infine, il gas riempie con densità uniforme tutto il volume a sua disposizione. Ecco una rappresentazione animata di tale modello:
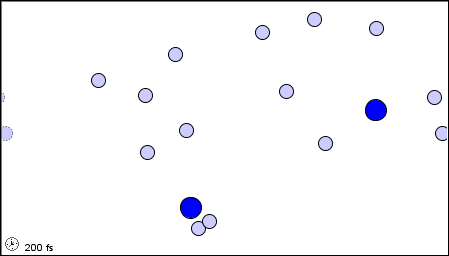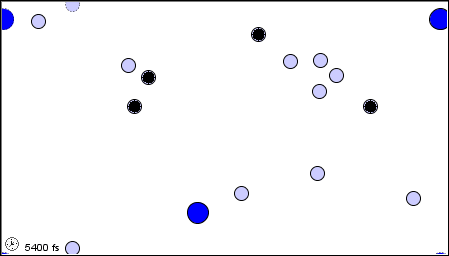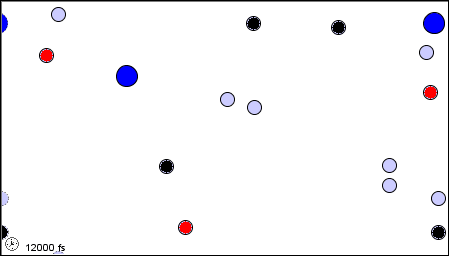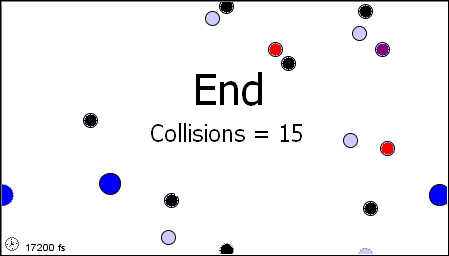
Il modello molecolare del gas perfetto (da questo sito)
Questo modello, come abbiamo visto, non è in perfetto accordo con il comportamento dei gas reali, per via della presenza di interazioni chimiche e di altro tipo, ma lo è tanto più quanto più il gas è rarefatto e lontano dalla temperatura di condensazione.
Supponiamo ora di voler effettuare un'analisi statistica di un sistema termodinamico, utilizzando le leggi della meccanica statistica. Per questo, occorre applicare ad ogni molecola le ben note leggi della meccanica classica, ma a questo punto sorge una difficoltà: per definire lo stato di un sistema occorre un numero enormemente grande di parametri, e cioè 3 N coordinate iniziali delle particelle e 3 N componenti delle velocità iniziali, dove N è dell'ordine del numero di Avogadro. Così si espresse in particolare il famoso scienziato illuminista Pierre Simon de Laplace (1749-1827) nell'introduzione al suo "Saggio filosofico sulla probabilità" (1812):
« Possiamo considerare lo stato attuale dell'universo come l'effetto del suo passato e la causa del suo futuro. Un intelletto che ad un determinato istante dovesse conoscere tutte le forze che mettono in moto la natura, e tutte le posizioni di tutti gli oggetti di cui la natura è composta, se questo intelletto fosse inoltre sufficientemente ampio da sottoporre questi dati ad analisi, esso racchiuderebbe in un'unica formula i movimenti dei corpi più grandi dell'universo e quelli degli atomi più piccoli; per un tale intelletto nulla sarebbe incerto ed il futuro proprio come il passato sarebbe evidente davanti ai suoi occhi. »

Pierre Simon de Laplace (1749-1827)
Questi calcoli non possono essere svolti con i nostri strumenti: appena il sistema raggiunge dimensioni dell'ordine delle migliaia di equazioni in migliaia di incognite, risulta praticamente impossibile conoscere la posizione e le velocità di tutte le molecole, e quindi seguirne l'incessante agitazione termica. D'altro canto, che senso avrebbe conoscere tutti questi risultati? Come può esserci utile, conoscere le proprietà differenziate delle singole molecole? A noi interessa il comportamento globale dell'intera popolazione di N molecole, ed esso può venire convenientemente descritto utilizzando delle grandezze medie, ottenute cioè mediando i parametri di tutte le molecole; e tali valori medi devono logicamente corrispondere alle grandezze macroscopicamente osservabili del nostro sistema termodinamico. Tutte le volte che si richiedono informazioni riguardo ad un numero grandissimo di oggetti, o quando un fenomeno è così complesso da escludere un'analisi diretta, così come ad esempio i programmi televisivi guardati da tutti gli abitanti di Milano, si ricorre ad un'analisi statistica. Così, se non ha alcun interesse sapere a quali programmi assiste la sera il signor Ermenegildo Bottazzi, è invece di grande interesse per le reti televisive conoscere la percentuale di telespettatori che assistono ai loro programmi ad una certa ora. Analogamente, nello studio di un sistema termodinamico non ha nessun senso conoscere l'evoluzione dinamica di una certa particella, mentre è possibile ricavare lo stato del sistema valutando statisticamente i valori medi e i valori più probabili delle grandezze microscopiche, come per esempio l'energia cinetica media delle molecole o il numero medio di molecole contenute in un recipiente. Del resto, le misure sperimentali di alcune grandezze macroscopiche, come la temperatura e la pressione, in realtà rappresentano solo i valori medi di alcuni parametri macroscopici, associati al movimento delle molecole. In un sistema in equilibrio termodinamico, infatti, le misure di queste grandezze medie forniscono, nell'ambito degli errori sperimentali, sempre lo stesso risultato, sicché le eventuali deviazioni sono troppo poco probabili per essere prese in considerazione.
Insomma, mediante l'analisi statistica noi ci disinteressiamo del singolo oggetto, e cerchiamo invece di valutare le proprietà medie dell'intero aggregato macroscopico, come fanno le indagini demoscopiche con i loro campioni di 10.000 utenti. Questo però non rappresenta affatto un "metodo approssimato" per "indovinare" il complesso comportamento di un sistema termodinamico. Si tratta invece di un metodo particolarmente efficace, al quale può sottostare ineluttabilmente ogni tipo di analisi riguardante un vasto numero di oggetti. Come scrisse Maxwell, « la vera logica di questo mondo è probabilistica » e, in parecchi casi, proprio il caso costituisce la migliore certezza. Se noi lanciamo una moneta dieci volte, potremmo ottenere quattro volte testa e sei volte croce; ma se la lanciamo un milione di volte, sarà praticamente certo il fatto che otterremo il 50 % di teste e il 50 % di croci. Infatti, secondo la Legge dei Grandi Numeri o Legge Empirica del Caso ideata dallo svizzero Jakob Bernoulli (1654-1705), al crescere del numero di prove, la frequenza tende ad uguagliare la probabilità matematica. E proprio il fatto che questa legge vale solo nel caso di grandi numeri, ci consente di applicare i metodi statistici alla termodinamica!
.
8.4 Approccio cinetico alla termodinamica
Ora ci addentreremo nella Teoria Cinetica dei Gas, con lo scopo di mostrare come si possa arrivare con questo metodo alla famosa equazione dei gas ideali P V = n R T. Cominciamo con l'analizzare i protagonisti di questa vicenda. Consideriamo un gas contenuto in un recipiente cubico di spigolo L, con i suoi spigoli paralleli agli assi cartesiani x, y e z, in modo che il suo volume risulti V = L3. Se il gas è concepito come una popolazione costituita da un numero immenso di molecole, immenso quanto la moltitudine dei salvati nell'Apocalisse di Giovanni, o come le schiere degli eserciti che si fronteggiano nelle epiche battaglie del "Signore degli Anelli", è logico che la pressione del gas contro le pareti del recipiente potrà venire interpretata come il risultato efficace degli urti delle molecole contro le pareti del recipiente. Siccome infatti essi sono tanto frequenti, danno l'idea di una azione continua. Applicando le leggi della meccanica classica al moto delle particelle, è possibile calcolare il valore della forza media (dovremo parlare necessariamente di grandezze medie) esercitata su ogni elemento della parete, e quindi la pressione. La temperatura sarà invece una stima dell'energia cinetica media posseduta dalle molecole.

La forza media esercitata dagli urti molecolari su di un elemento di superficie ΔS della parete rigida del recipiente contenente il gas può essere calcolata come il rapporto tra la quantità di moto scambiata tra la parete e le molecole che la urtano, e l'intervallo di tempo Δt in cui tale scambio avviene. Naturalmente nel calcolo l'intervallo di tempo considerato deve essere così breve da poter ottenere un valore pressoché istantaneo, ma lungo rispetto all'intervallo medio tra due urti successivi; ciò è lecito, visto il gran numero di molecole del sistema. L'angolo di incidenza è notoriamente pari all'angolo di riflessione, e il modulo della quantità di moto p della particella incidente è pari a quella della particella riflessa, perchè l'urto è elastico. Come si vede dalla figura qui sopra allora si ha:
| Δp | = 2 p cos θ = 2 m v cos θ (8.7)
Naturalmente v cos θ è la componente della velocità perpendicolare alla parete. Ne consegue che l'effetto degli urti obliqui sulle pareti del recipiente è indistinguibile da quello degli urti diretti perpendicolarmente alla parete. A questo punto, aggiungiamo delle ipotesi semplificative. Supponiamo che tutte le molecole si muovano in direzione perpendicolare alle pareti, cioè parallelamente ai tre assi coordinati x, y, z. Vista l'isotropia delle velocità, ogni direzione del moto è equivalente alle altre. Possiamo perciò ipotizzare che un terzo delle molecole si muova parallelamente all'asse x, un terzo parallelamente all'asse y e un terzo parallelamente all'asse z. Tutte le molecole inoltre si muovono con la stessa velocità, che necessariamente sarà rappresentata da un valore medio. Ma quale valore medio? Consideriamo N molecole che hanno la stessa massa m e velocità v1, v2, ..., vn. L'energia cinetica media di traslazione delle molecole è:
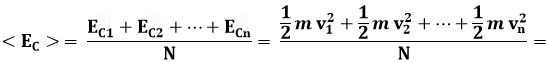
![]()
Ci accorgiamo che la seconda frazione rappresenta il momento di ordine due della distribuzione di velocità.
Def. 8.9: Dicesi velocità quadratica media delle molecole la radice quadrata di tale valore:
![]()
Di conseguenza potremo calcolare l'energia cinetica media delle molecole usando questa formula:
![]()
A partire dalla (8.7), la quantità di moto ceduta alla parete sarà allora:
| Δp | = 2 m < v >

Una volta urtata una parete, ogni molecola percorre una distanza L, pari allo spigolo del nostro recipiente cubico, fino alla parete opposta, rimbalza contro di essa, percorre un'altra distanza L e ritorna alla parete di partenza. Quindi, tra un urto e l'altro sulla medesima parete la particella percorre una distanza 2 L. Poiché si muove con velocità < v >, per percorrere tale distanza impiega un tempo pari a:
![]()
Questo è l'intervallo medio di tempo tra due urti successivi. A questo punto, bisogna applicare la cosiddetta Prima Equazione Cardinale della Dinamica, secondo la quale la forza esercitata dalla parete dalla singola molecola è pari alla quantità di moto da essa trasmessa alla parete nell'unità di tempo:
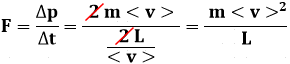
Ma allora la forza complessiva Ftot esercitata sulla parete del recipiente cubico dalle N / 3 molecole che cozzano contro di essa si ottiene moltiplicando la forza ora calcolata per N / 3:
![]()
E di conseguenza la pressione esercitata dal gas contro la parete è ottenibile dividendo tale forza per l'area L2 della parete:
A questo risultato si può arrivare in modo rigoroso anche usando gli strumenti dell'Analisi Matematica; chi non ne possiede i suoi strumenti, salti pure alla conclusione. Nell'intervallo Δt, di urti se ne verificano n1. Questo, evidentemente, è il numero di particelle contenute in un cilindretto di base dS e di inclinazione θ, il cui asse misura v dt. Anche questo numero è grande in assoluto, ma piccolo rispetto al numero totale di molecole contenute nel sistema.
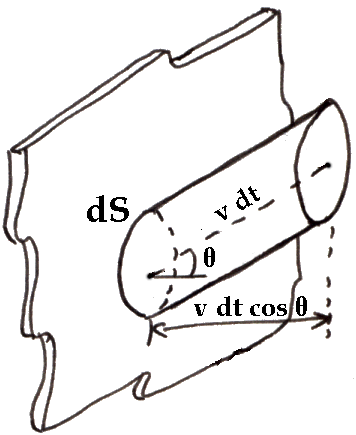
Sia allora N il numero totale di molecole contenute nel sistema; n1 si può calcolare moltiplicando N per la probabilità che una molecola a caso cada nel cilindretto rappresentato qui sopra, e poi per la probabilità che la velocità abbia inclinazione compresa tra θ e θ + dθ rispetto alla normale alla parete, e per la probabilità che il modulo della velocità sia compreso tra v e v + dv.
Se y(v) è la distribuzione delle velocità delle nostre particelle, che studieremo nel capitolo successivo, allora la probabilità che la velocità cada tra v e v + dv è semplicemente y(v) dv. La probabilità che le molecole cadano nel volumetto prefissato è dV/V, dove dV è l'elemento di volume sopra descritto, complessivamente pari a:
dV = v dt dS cos θ
Quanto alla probabilità che la direzione cada in un angolo prefissato, bisogna ricorrere al concetto di angolo solido. Come è noto, l'angolo piano è pari al rapporto tra l'arco e il raggio; analogamente, l'angolo solido è pari al rapporto tra la porzione di superficie sferica contenuta in tale angolo e il quadrato del suo raggio. Siccome la lunghezza della circonferenza di raggio R è pari a 2 π R, l'angolo giro misurerà 2 π R / R = 2 π radianti. E siccome la superficie sferica complessiva misura 4 π R2, l'angolo solido totale (che comprende tutte le possibili direzioni) misurerà 4 π R2 / R2 = 4 π steradianti.
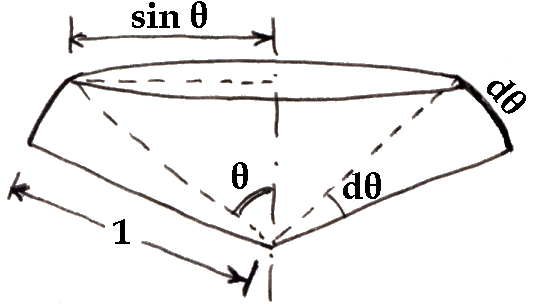
Detto Δω l'elemento di angolo solido, la probabilità che la direzione della velocità cada in un angolo prefissato è dω / 4 π. Allora, per definizione di angolo solido, dalla figura soprastante risulta che:
![]()
da cui:
![]()
Perciò, in definitiva:
![]()
La quantità di moto complessiva, esercitata dalle molecole contro le pareti del recipiente, si ottiene integrando dp x n1 su tutti i possibili valori dell'angolo θ tra 0 e 2 π, e su tutti i possibili valori di v tra 0 e + ∞. Abbiamo così:

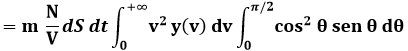
Questa è la quantità di moto ricevuta dall'area dS nel tempo dt, e cioè la quantità di moto per unità di superficie e di tempo. Ora, l'integrale:
![]()
è il momento di ordine due della variabile v, definito dalla (8.6), e di conseguenza rappresenta la media dei quadrati delle velocità, che tramite la (8.8) abbiamo definito < v2 >. Si tratta del quadrato della velocità quadratica media < v >.
Inoltre, mediante la sostituzione cos θ = t:
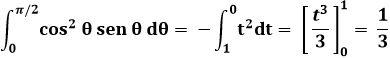
Da cui si ricava:
![]()
Ma la quantità di moto per unità di superficie e di tempo è proprio la pressione, come ci conferma l'equazione dimensionale:
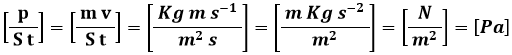
E così posso immediatamente ricavare la pressione secondo la Teoria Cinetica dei Gas:
![]()
E questo è il risultato espresso dalla (8.9), che avevamo già trovato sopra per via approssimata!
.
8.5 La temperatura dal punto di vista cinetico
Riprendiamo ora in mano la (8.9). Se n è il numero di moli del gas contenuto nel volume V, si ha N = n NAV, dove NAV è il numero di Avogadro. Sostituendola nell'espressione cinetica della pressione, si ha:
Ora rispolveriamo la costante di Boltzmann introdotta nel § 7.4:
![]()
La precedente allora può essere così riscritta:

Confrontiamola con l'equazione di stato dei gas perfetti, espressa dalla (3.3):
![]()
Si constata subito che le due equazioni coincidono a patto di identificare:
Moltiplicando entrambi i membri per 3 KB/2 la precedente diventa:
La (8.11) è la definizione di temperatura assoluta nella Teoria Cinetica dei Gas, mentre la (8.12) ci dice che la temperatura assoluta è direttamente proporzionale al valor medio < EC > dell'energia cinetica posseduta dalle molecole. In definitiva, dunque, un corpo caldo è un sistema in cui le molecole possiedono una grande energia cinetica. Ciò significa, in accordo con l'intuizione, che le molecole sono animate da una fortissima agitazione termica, che risulta tanto maggiore quanto maggiore è la temperatura assoluta. Accostando due corpi a temperatura differente, l'agitazione termica si trasmette da una particella all'altra per mezzo degli urti: quelle più veloci cedono una parte della loro energia a quelle più lente, per cui le veloci rallentano un po', e le più lente accelerano un po', arrivando alfine ad un valore medio.

|
Ecco un ingegnoso meccanismo per illustrare il modello cinetico dei gas: un cuscino d'aria fa muovere dei bottoni di plastica che simulano le molecole, e modellizza un insieme di particelle di dimensioni trascurabili che interagiscono senza attrito solo per urti elastici |
La (8.12) vale non solo per i gas perfetti, ma anche per i liquidi ed i solidi, se si considera il solo moto di traslazione delle molecole, e non quello di rotazione o di vibrazione. Essendo il prodotto di una massa (sempre positiva) per il quadrato di una velocità, l'energia cinetica media < EC > non può essere negativa. Di conseguenza, come del resto già sappiamo, anche secondo la Teoria Cinetica dei Gas la temperatura assoluta T di un corpo non può assumere valori negativi. Il suo valore minimo possibile è zero Kelvin. Ecco perchè tale temperatura è definita zero assoluto: essa è la minima temperatura possibile, e non è assolutamente possibile raffreddare un sistema termodinamico al di sotto di essa. A T = 0 K corrisponde < EC > = 0: dunque allo zero assoluto tutte le molecole sono ferme, e non possono essere raffreddate ulteriormente. Ecco perché la temperatura di un sistema non può scendere al di sotto di questa soglia. Ciò spiega anche perchè, secondo la legge di Charles, a T = 0 K si ha V = 0: secondo il modello di gas perfetto appena esposto, le molecole non hanno volume, e quindi anche il volume del condensato è nullo.
Esempio 8.1: In una lampada al neon spenta, la temperatura del gas è pari a 23°C. Quanto vale l'energia cinetica media delle molecole di neon contenute nella lampada?
Dato che le molecole di neon sono monoatomiche, trattandosi di un gas perfetto, e quindi puntiformi, esse possono traslare ma non ruotare e vibrare, e quindi si può applicare la (8.12). Siccome T = 23 + 273,15 = 296,15 K., si ottiene:
![]()
.
8.6 La propagazione sonora nei gas
Confrontando la (8.10) e la (8.11) si constata che in entrambe le definizioni di P e di T compare la velocità quadratica media < v2 >. Ma questa si può calcolare anche per via macroscopica? Certo. Se m è la massa di una molecola, m N è la massa dell'intero gas, e quindi m N / V è la densità del nostro gas, che indicheremo con la lettera greca ρ. La (8.10) perciò si può riscrivere:
![]()
e di conseguenza:
Esempio 8.2: Se so che 1,2 Kg di gas perfetto sono contenuti in un volume di 1000 litri alla pressione atmosferica, quanto vale la velocità quadratica media delle sue molecole?
Basta usare la (8.13) ed avremo:
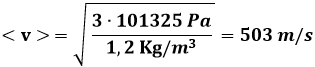
Esempio 8.3: Qual è la velocità quadratica media delle molecole d'aria a 25°C e un'atmosfera di pressione?
Poiché P = 101.325 Pa e T = 298 K, prendiamo un metro cubo di aria. Si ha:
![]()
E poiché, come già sappiamo, la mole d'aria vale 28,84 g, si ha:
m = 40,9 mol x 28,84 g / mol = 1,179 Kg
da cui ρ = 1,179 Kg / m3. Ne segue < v > = 507,6 m / s.
Osserviamo che tale valore è vicino a quello della velocità di propagazione del suono nell'aria. Questo ci consente di spiegare brevemente il meccanismo microscopico di propagazione del suono.
Oltre al disordinato moto di agitazione termica, in questo caso, le molecole devono possedere anche un moto ordinato lungo la direzione di propagazione, dal quale si origina, in seguito agli urti, una trasmissione di energia cinetica molecolare, che noi percepiamo sotto forma di energia sonora. Benché le molecole possiedano in media una velocità abbastanza elevata, esse a causa degli urti non si spostano di molto nella direzione di propagazione del suono. Ciò che si propaga è piuttosto l'energia sonora, con lo stesso ordine di grandezza dell'energia cinetica media molecolare.
A causa degli urti, del resto, la diffusione molecolare è sempre piuttosto lenta; e infatti, aprendo in una stanza chiusa una boccetta di profumo, occorre sempre un certo tempo prima che il profumo si avverta in un altro punto della stanza, come chiunque può constatare.

In un gas le molecole sono libere di scorrere le une sulle altre, e quindi il suono si propaga solo per mezzo di onde di pressione longitudinali. Ad esempio, un diapason messo in vibrazione genera una successione di perturbazioni di compressione ed espansione. Tale successione è percepita dall'orecchio umano come un suono. In genere le compressioni e le espansioni causate dal suono nel fluido sono troppo deboli perché vi sia una variazione apprezzabile di entropia, per cui possiamo considerare il processo isoentropico.
Per ricavare l'espressione della velocità del suono nei gas è indispensabile utilizzare il formalismo dell'Analisi Matematica; come sempre, chi non lo possiede salti pure alla conclusione. Applichiamo il principio di conservazione della massa ed il principio di conservazione della quantità di moto. Prima del passaggio dell'onda la velocità media del gas avrà sempre il valore vS e la pressione il valore P, mentre dopo di essa la velocità sarà diminuita se l'onda sonora è di compressione (o aumentata se l'onda è di espansione) al valore vS − d v; la pressione e la densità saranno aumentate (o diminuite) al valore P + d P e ρ + d ρ rispettivamente. Poiché la massa deve conservarsi, la portata in massa che l'onda attraversa deve essere uguale a quella che l'onda si lascia alle spalle; la portata è pari al prodotto della densità per la velocità, e quindi:
ρ a = ( ρ + d ρ ) ( vS − d v )
Sviluppiamo il tutto. Il prodotto di due variazioni è un infinitesimo di ordine superiore, per cui può essere trascurato:
vS d ρ = ρ d v (8.14)
Oltre alla massa poi deve conservarsi anche la quantità di moto, e allora:
P − ( P + d P ) = m [ ( vS − d v ) − vS ]
Sviluppiamo anche questa:
d P = ρ vS d v (8.15)
Infine, eliminando d v tra le due equazioni (8.14) e (8.15), otteniamo:
Ora, nel § 6.3 si è visto che:
![]()
Se il processo è isoentropico, dS = 0, e la precedente fornisce:
![]()
Dividendo entrambi i membri per cV, e ricordando che γ = cP / cV è il coefficiente di dilatazione adiabatica, già introdotto nel § 4.7, si ha:
![]()
Ora, facciamo ricorso all'equazione di stato dei gas perfetti e dividiamone ambi i membri per il volume
![]()
dove A è la grammomolecola, cioè la massa molecolare del gas. Ne consegue che la (8.16) diventa:
![]()
E quindi si può ricavare la formula che fornisce la velocità del suono:
Esempio 8.4: Determinare la velocità dell'aria a 15°C.
L'aria è un gas biatomico con A = 28,84 g/mol, per esso γ = 7/5 = 1,4, e quindi per la (8.17):
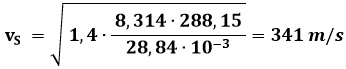
Esso coincide con il valore comunemente accettato della velocità del suono nell'aria. Come si vede, vS dipende solo dalla temperatura assoluta alla quale il gas si trova. Ad esempio, a − 10°C la velocità del suono nell'aria è di circa 325 m/s, e a + 30°C sale a 349 m/s: provare per credere.
.
A questo punto, dobbiamo approfondire il concetto di distribuzione maxwelliana di velocità. Per farlo, passate con me al capitolo seguente, nel quale avremo ancora a che fare con formule molto complicate. Per tornare all'indice, invece, il link è questo.
![]()