Le transizioni di fase

.

2.1  I passaggi di stato

Def. 2.1: Dicesi sistema aperto un sistema che scambia con l'esterno tanto materia quanto energia. Dicesi sistema chiuso un sistema che scambia con l'ambiente esterno solo energia, ma non materia. Dicesi infine sistema isolato un sistema che non scambia con l'ambiente esterno né materia né energia.

Un esempio di sistema aperto è la stanza in cui vi trovate in questo momento: essa scambia materia con l'esterno perchè nessuna chiusura è ermetica, e attraverso le fessure trafila aria, e scambia anche energia perché le pareti non sono adiabatiche. Un sistema chiuso è una stanza ermeticamente chiusa attraverso le cui pareti può comunque passare calore. Un sistema perfettamente isolato a rigore non esiste, stante l'impossibilità di creare pareti perfettamente adiabatiche; tuttavia normalmente si dice che l'intero universo è un esempio di sistema isolato. Normalmente nel seguito noi prenderemo in considerazione unicamente sistemi chiusi.

È ben noto il fatto che una stessa sostanza può presentarsi in diversi stati, detti stati di aggregazione della materia, a seconda di come le molecole sono in relazione tra di loro. Se le posizioni relative delle molecole sono fisse, ed esse possono al massimo vibrare intorno alla posizione di equilibrio, allora la sostanza è solida, ed è dotata sia di forma che di volume propri. Se le molecole possono scorrere l'una sull'altra, ma non separarsi tra di loro, la sostanza è liquida, ed è dotata di volume proprio, ma non di forma propria, assumendo quella del recipiente che la contiene. Se le molecole possono separarsi l'una dall'altra, allora la sostanza è aeriforme, e non è dotata né di forma né di volume proprio, ma assume quelli del recipiente che la contiene. Liquidi e aeriformi prendono anche il nome di fluidi. Esistono altri tre stati di aggregazione della materia: plasma, condensato di Bose-Einstein e plasma di quark e gluoni. Il primo è uno stato aeriforme elettricamente carico, in cui gli elettroni sono separati dai nuclei; il secondo e il terzo sono stati esotici della materia, che esistono solo in condizioni particolari e non nell'ambiente in cui si svolge la vita di tutti i giorni. Per questo, di questi tre stati di aggregazione in questo ipertesto noi non parleremo.

Questi stati di aggregazione non sono separati l'uno dall'altro, ma è possibile passare dall'una all'altra con le seguenti trasformazioni:

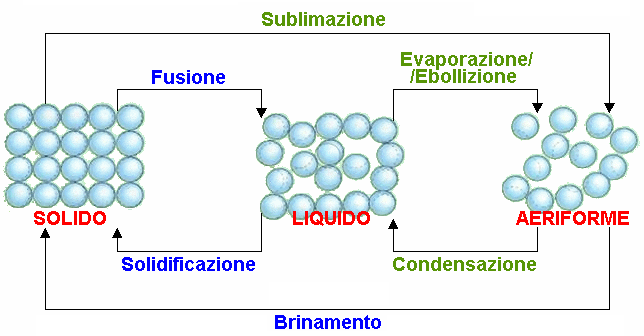
Come si vede, il passaggio di stato da liquido ad aeriforme può avere due nomi diversi, perchè può avvenire secondo due modalità diverse. La differenza tra evaporazione ed ebollizione sta nel fatto che la prima riguarda solo lo strato superficiale del liquido, mentre la seconda interessa tutto il suo volume, per via dei moti convettivi all'interno di esso. Se porto un solido alla temperatura di fusione, ad essa solido e liquido sono in equilibrio fra di loro. Idem si dica per un liquido e il suo vapore alla temperatura di evaporazione. Proviamo allora a rappresentare quella che si chiama la curva di riscaldamento di una sostanza (in genere in laboratorio per la didattica si usa acido stearico). Mettiamo in ascisse il tempo e in ordinate la temperatura, e somministriamo calore al corpo a tasso costante; ciò significa che in ascisse si può mettere anche il calore somministrato al corpo.

Operiamo a pressione costante. Io vedo salire la temperatura del solido fino a che non comincia la fusione (area azzurra sottostante), poi essa resta costante durante tutto il passaggio di stato (area verde). Si parla in tal caso di "sosta termica". Ricomincia a crescere quando tutto il solido è fuso (area rosa); la temperatura cresce fino a che il liquido non comincia a bollire; allora si ha una seconda sosta termica, che dura fino a che il passaggio di stato non è concluso (area blu); quindi, la temperatura cresce un'altra volta. Quella che si ottiene è la cosiddetta curva di temperatura della sostanza considerata:

Contrariamente a quanto si è detto finora, nel corso delle due soste termiche viene ceduto calore al corpo senza che questo aumenti la propria temperatura. Come mai? Perchè, mentre ciò avviene, il calore non serve ad alzare la temperatura del corpo, bensì a rompere i legami molecolari, il che comporta l'"allentamento" dell'energia di legame da solido a liquido, e da liquido a gas. La pressione parziale del vapore nella miscela liquido-aeriforme durante la transizione di fase si dice tensione di vapore (anche se non è una forza ma una pressione). Poiché questa miscela liquido-vapore è all'equilibrio con l'ambiente esterno, se ne deduce che si ha ebollizione solo se la tensione di vapore uguaglia la pressione esterna. Infatti, quando metto a bollire una pentola sul fuoco, il fondo di essa è a contatto diretto con la sorgente di calore e si scalda per primo, generando bolle di vapore sul fondo del liquido. Il vapore ha densità minore del liquido e quindi, per il Principio di Archimede, sale verso l'alto, causando la discesa di acqua più fredda, che si scalderà a sua volta; nascono così i moti convettivi, facilmente visibili quando si buttano i maccheroni nell'acqua che bolle. Se però la pressione all'interno delle bolle che si formano sul fondo della pentola (cioè la tensione di vapore) è inferiore alla pressione esterna dell'atmosfera e a peso dell'acqua, le bolle vengono schiacciate, e si ha ebollizione in tutta la massa del liquido solo quando la tensione di vapore diventa sufficientemente alta.

Questo significa che la temperatura di ebollizione di un liquido dipende dalla pressione esterna; al crescere di questa, la sosta termica di ebollizione si alza, come mostra la seguente tabella:

Più avanti ricaveremo l'andamento della temperatura di ebollizione in funzione della pressione esterna. Se l'acqua bolle al 100°C a livello del mare, cioè alla pressione di 1 atmosfera, a 3000 metri di quota essa bolle a temperatura più bassa, perchè la pressione esterna è minore, essendo legato al peso della colonna d'aria sovrastante (lo dimostra il fastidio che si prova alle orecchie durante il cambio di altitudine: la variazione della pressione atmosferica non è bilanciata da un'uguale variazione della pressione che agisce sulla parte interna del timpano. Sbadigliando o deglutendo si ripristina l'equilibrio). Dunque, a 3000 metri l'acqua bolle prima, e la pastasciutta rischierebbe di venire scotta. Non esiste una relazione precisa tra la quota e la pressione, poiché possono influenzarla altri fattori come la temperatura e l'umidità; approssimativamente si può assumere che alle basse quote la pressione diminuisca di 100 Pascal ogni 8 metri. Ecco la pressione atmosferica approssimativa ad alcune quote:

Confrontando le due tabelle, si deduce che a 3000 metri l'acqua bolle a 90°, a 5.500 metri bolle a circa 80° e a 12.000 metri bolle a 60°.

Al contrario, se la pressione è maggiore, l'acqua bolle a temperatura più elevata, e quindi più lentamente. È questo il principio sul quale si basa il principio della cosiddetta pentola di Papin, che ha dato il titolo a questo ipertesto. Ideata dal fisico francese Denis Papin (1647-1712), essa consiste in un recipiente ermeticamente chiuso per mezzo di una guarnizione, che viene messo a bollire sul fuoco; onde evitare che scoppi, vi è una valvola di sicurezza che lascia uscire il vapore in eccesso se la pressione diventa troppo alta. All'aumentare della pressione si alza la temperatura di ebollizione dell'acqua, e quindi per raggiungerla occorre più tempo; di conseguenza i cibi cuociono più a lungo e meglio. Non è certo un caso se Papin la brevetto nel 1679 con il nome di "digestore", essendo in grado di rendere i cibi molto più digeribili e di preservare molti preziosi principi nutritivi. Solo nel 1864 però il tedesco Georg Gutbrod iniziò a commercializzare pentole a pressione fabbricate in ghisa. Esse cominciarono a diffondersi in ogni casa con il boom economico seguito alla Seconda Guerra Mondiale.

Modello ottocentesco di pentola di Papin

Il fenomeno dell'ebollizione tra l'altro è ben noto anche a Dante Alighieri, che all'inizio del XXXIII canto dell'Inferno scrive:

« Quale ne l'arzanà de' Viniziani
bolle l'inverno la tenace pece
a rimpalmare i legni lor non sani [...]
tal, non per foco ma per divin' arte,
bollia là giuso una pegola spessa,
che 'nviscava la ripa d'ogne parte.
I' vedea lei, ma non vedëa in essa
mai che le bolle che 'l bollor levava,
e gonfiar tutta, e riseder compressa » (Inf. XXI, 7-9.16-21)

Nella Quinta Bolgia, quella dei Barattieri, a Dante sembra di essere nell'Arzanà, cioè nell'Arsenale di Venezia, costruito ai primi del XII secolo, che ai suoi tempi era il più attivo d'Europa (la voce veneta Arzanà ricalca l'arabo Dar sina'a, "casa di fabbricazione"). Infatti durante l'inverno, stagione poco propizia alle navigazioni di lungo corso, le navi venivano calafatate e rattoppate con pece bollente, la stessa di cui è zeppa la Bolgia. In quella "tenace pece", quella "pegola spessa" che invischia, cioè ricopre di una massa appiccicosa sia l'arsenale veneziano che quell'oscuro angolo infernale, Dante non vede altro che le bolle che salgono continuamente in superficie coinvolgendo tutto il volume del fluido, proprio come nel fenomeno dell'ebollizione: il Sommo Poeta vede la superficie della pece sollevarsi tutta, come fa un liquido viscoso che trattiene in sé del vapore, e subito dopo ricadere giù sgonfiandosi, come anche noi abbiamo visto fare ad esempio alla polenta che si rimescola nel paiolo!

.

2.2  I calori latenti

Def. 2.2: Si dice calore latente di fusione, indicato con il simbolo λ_fus, il calore che l'unità di massa di solido deve assorbire per trasformarsi interamente in liquido. Di conseguenza:

Q_fus = m λ_fus

Def. 2.3: Si dice calore latente di evaporazione, indicato con il simbolo λ_ev, il calore che l'unità di massa di liquido deve assorbire per trasformarsi interamente in vapore. Analogamente al caso precedente:

Q_ev = m λ_ev

λ_fus e λ_ev si misurano in J/Kg. Eccone alcuni valori:

Esempio 2.1: Calcolare il calore che si deve somministrare a 10 kg di ghiaccio, inizialmente alla temperatura di – 5°C, per ottenere acqua a 20°C.

Trovandosi il ghiaccio a – 5°C, occorre prima somministrargli calore per portarlo a 0°; a questo punto bisogna cedergli calore per farlo fondere, quindi bisogna somministrargli il calore latente di fusione; poi devo cedere all'acqua a 0°C il calore necessario per portarlo a 20°C. λ_fus del ghiaccio è desumibile dalla tabella soprastante, mentre il calore specifico dell'acqua vale 4186 J/Kg °C e quello del ghiaccio vale 2040 J/Kg °C. Ne consegue che il calore richiesto è:

Q = m c_gh (T_fus – T_iniz) + m λ_fus + m c_acqua (T_fin – T_fus) =

= 10 Kg x 2040 J/Kg °C x 5°C + 10 Kg x 333.500 J/Kg + 10 Kg x 4186 J/Kg °C x 20°C =

= 102.000 J + 3.335.000 J + 837.200 J = 4.274.200 J

Esempio 2.2: In un calorimetro ideale sono presenti 3 litri di acqua a 25°C. In essa inserisco 0,5 Kg di ghiaccio a – 15°C. Determinare la temperatura finale all'equilibrio.

Stavolta il procedimento è un po' diverso da quello del problema analogo dell'Esempio 1.4. Infatti, se m₁ è la massa dell'acqua, il calore da essa ceduto è pari semplicemente a m_acqua c_acqua (T₁ – T_eq). Quanto al ghiaccio, questo calore deve prima scaldarlo fino a 0°C, poi fonderlo ed infine portarlo a + 25°C. Perciò avremo l'equazione:

m_acqua c_acqua (T₁ – T_eq) = m_gh c_gh (T_fus – T₂) + m_gh λ_fus + m_gh c_acqua (T_eq – T_fus)

Sostituendo i valori numerici (m_acqua = 3 kg, m_gh = 0,5 Kg T₁ = 25°C, T₂ = – 15°C) si ha T_eq = 9°C circa.

Osservazione. Quanto detto in questo paragrafo può aiutarci a capire perchè si verifica un fenomeno stranissimo, noto come la "cascata di sangue dell'Antartide". Esso fu scoperto nel 1911 dall'esploratore britannico Thomas Griffith Taylor (1880-1963) nelle cosiddette Valli Secche di McMurdo. Poste alle coordinate di 77° 30′ Sud e 162° 00′ Est, esse rappresentano la più estesa superficie libera dai ghiacci in Antartide e comprendono il fiume Onyx, il più lungo fiume del Sesto Continente. Proprio in questo luogo così remoto dalle zone abitate del globo, è possibile assistere ad un fenomeno che definire inquietante è dire poco. Come si vede nella foto sottostante, scattata da Erin C. Pettit, inclusa nel candore del ghiaccio c'è infatti una cascata color rosso sangue, composta da acqua salmastra che si getta nel lago Bonney: il colore rosso è dovuto agli ossidi di ferro contenuti nell'acqua salmastra, che diventano di questo colore a contatto con l'ossigeno dell'aria. Nessuno però aveva mai capito da dove proviene l'acqua salata, dato che la zona è lontana dal mare e le Valli Secche di McMurdo, come recita il loro nome, sono una delle località con l'umidità e le precipitazioni più basse del mondo.

Nel 2017 però un team di ricercatori guidato da Jessica Badgeley dell'Università del Colorado e da Erin C. Pettit dell'Università dell'Alaska a Fairbanks ha risolto il mistero che durava da 106 anni: l'acqua di mare è stata intrappolata più di un milione di anni fa in una riserva sotto il ghiacciaio Taylor, e percorre un tratto di circa 90 metri prima di comparire in superficie: il percorso è stato tracciato tramite un radar. Ma come è possibile che esista acqua liquida in un ambiente così freddo, dove la temperatura media annuale dell'aria è di – 17°C? Semplice: nel momento in cui congela, come si è visto l'acqua rilascia una certa quantità di calore, e questo calore latente riscalda il ghiaccio circostante. Il calore e il contenuto salino dell'acqua, che gela a una temperatura inferiore, consente la presenza di acqua allo stato liquido. Per questo motivo, il ghiacciaio Taylor è il più freddo al mondo dove è presente in modo continuativo acqua liquida!

.

2.3  Il diagramma delle fasi

È possibile rappresentare su un unico diagramma tutte le fasi che una sostanza può presentare al variare della pressione e della temperatura, ed anche gli stati in cui le varie fasi sono all'equilibrio tra di loro. Si tratta in particolare di un diagramma che ha la temperatura assoluta in ascisse e la pressione in ordinate. Si è detto in quel che precede che, al crescere della pressione, la temperatura di ebollizione sale, quindi la linea di transizione di fase sarà crescente. Come vedremo nel seguito, è la linea qui sotto a sinistra:

Sopra sta il vapore, sotto lo stato liquido. Analoga è la linea di sublimazione, che separa il solido dal vapore, mentre quella che separa il solido dal liquido deve essere quasi verticale, poiché si può dimostrare che la pressione influenza assai poco la temperatura di liquefazione, essendo il solido quasi incomprimibile: occorrono pressioni altissime per modificarne di poco il volume. Si ottiene in tal modo il diagramma seguente:

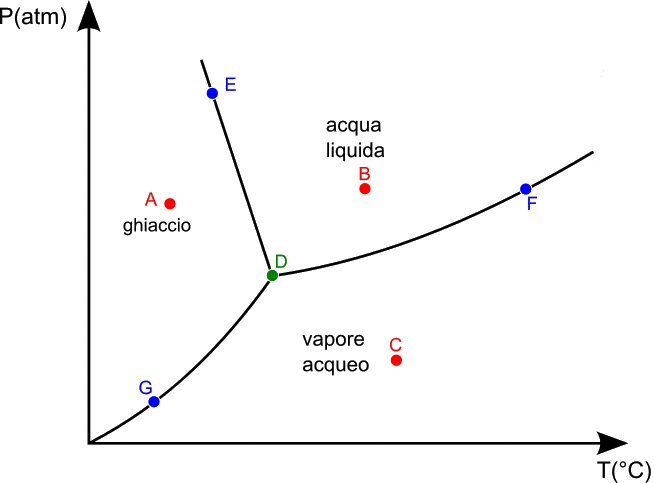
A seconda di dove cade il punto ( P ; T ) si può decidere se il corpo si trova in fase solida, liquida o aeriforme. Si parla per questo di diagramma delle fasi. Il punto A di colore rosso rappresenta uno stato in fase solida, il punto B uno in fase liquida, il punto C in fase vapore. Invece il punto E di colore blu rappresenta uno stato bifase in cui coesistono ghiaccio ed acqua liquida; il punto F ne rappresenta uno in cui coesistono acqua liquida e vapore acqueo; il punto G rappresenta uno stato bifase in cui coesistono ghiaccio e vapore. Invece il punto D in verde rappresenta un caso unico, in quanto in esso coesistono ghiaccio, acqua liquida e vapore acqueo. In altre parole, esistono una pressione ed una temperatura alle quali le tre fasi coesistono. Tale punto si dice punto triplo, ed è caratteristico di ogni sostanza. Per l'acqua, il punto triplo si ha per i valori di T = + 0,01°C e P = 4,58 torr.

Se parto da uno stato ( P ; T ), mantengo costante la pressione ed aumento la temperatura. Mi sposto così verso destra; prima c'è il passaggio di stato da solido a liquido, poi da liquido ad aeriforme. Si noti che sul diagramma non sono indicati né il tempo né il calore necessari alla transizione di fase, a differenza del diagramma mostrato sopra, per cui il passaggio di stato nel diagramma delle fasi appare puntiforme, senza alcun tratto orizzontale. Se però alzo la pressione, cioè se seguo un tragitto più in alto, la transizione di fase è incontrata a temperatura più alta; e vale anche il viceversa. Al di sotto di una certa pressione, si ha sublimazione senza alcun passaggio allo stato liquido. Questo è molto importante: infatti anche il ferro ha una tensione di vapore, per quanto piccolissima. Se pratico il vuoto spinto in un ambiente dove è presente del ferro, anche alla temperatura ambiente questo comincia a sublimare, cioè alcuni atomi superficiali di ferro passano allo stato gassoso. Di conseguenza, ottenere il vuoto assoluto dentro un recipiente è impossibile, perchè in tali condizioni le pareti comincerebbero ad evaporare!

.

2.4  La regola delle fasi

L'esistenza del punto triplo ci porta a domandarci: qual è il numero di fasi diverse che possono coesistere in un sistema? Risponde a questa domanda la regola di Gibbs o regola delle fasi. Si consideri un sistema termodinamico formato da c componenti (specie chimiche) diverse, con f fasi distinte. Il numero di gradi di libertà del sistema, cioè il numero di variabili che possono cambiare valore indipendentemente dalle altre, si chiama varianza v del sistema. Se v è negativa, il sistema non può sussistere. Se è nulla, non ho alcun grado di libertà, cioè il sistema esiste per un solo ben preciso valore di due parametri. La regola delle fasi afferma dunque che:

v = c + 2 – f

Esempio 2.3: Si consideri l'acqua allo stato liquido, come nel punto B in figura. Ovviamente è presente una sola specie chimica (c = 1) e una sola fase (f = 1). Si ha perciò:

v = 1 + 2 – 1 = 2

Posso dunque variare liberamente due parametri, ed infatti cambiando sia la pressione che la temperatura posso restare in fase liquida nel diagramma delle fasi. Di conseguenza, un sistema monofase è rappresentato da una porzione di superficie nel diagramma delle fasi-

Esempio 2.4: Consideriamo un sistema bifase formato da acqua liquida e vapore d'acqua in equilibrio termodinamico tra di loro, come nel punto F in figura. La specie chimica è sempre una sola (c = 1), ma stavolta ho due fasi (f = 2), per cui:

v = 1 + 2 – 2 = 1

Infatti, se vario la pressione non ho più un sistema bifase, a meno di non variare anche la temperatura. Per conservare le due fasi distinte devo muovermi lungo la linea che rappresenta l'evaporazione, e quindi se vario un parametro non posso variare liberamente anche l'altro. Di conseguenza, un sistema bifase è rappresentato da una linea nel diagramma delle fasi.

Esempio 2.5: Consideriamo un sistema trifase, nel quale cioè coesistono tre fasi, come nel punto D in figura. Stavolta f = 3, quindi:

v = 1 + 2 – 3 = 0

Si tratta di un sistema zerovariante, nel quale non posso cambiare alcun parametro, altrimenti una delle fasi inevitabilmente sparisce. Infatti, come si è detto sopra, il punto triplo è rappresentato da un punto solo nel diagramma delle fasi!

A questo punto, un attimo di attenzione. Le fasi possono essere anche più di tre, perchè possono sussistere (per quanto paia incredibile) diverse fasi solide, con differenti strutture cristalline. Tipicamente, è il caso dello zolfo, che possiede due fasi solide: rombica e monoclina. In condizioni normali lo zolfo è rombico, tipicamente giallo, opaco e fragile, ma a 95,6°C dà vita a una nuova fase solida, quella monoclina, i cui cristalli sono a forma di ago, cerosi e fragili. Se voglio che coesistano zolfo rombico, zolfo monoclino e vapore, allora v = 1 + 2 – 3 = 0. Essendo nulla la varianza, compare un nuovo punto triplo a 118,7°C, e un terzo compare a 151°C, dove coesistono fase rombica, fase monoclina e fase liquida. Ecco come appare allora il diagramma delle fasi dello zolfo:

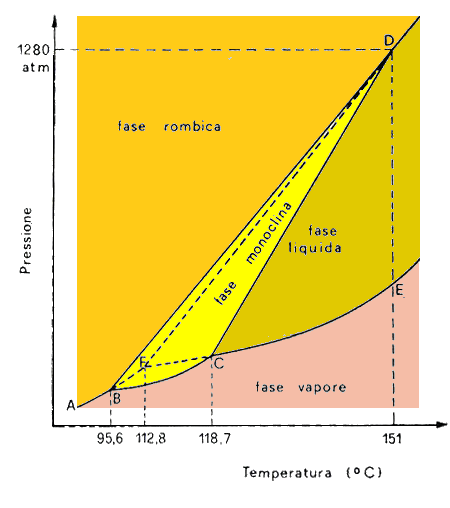
E se volessi quattro fasi? Con f = 4 avrei v = 1 + 2 – 4 = – 1, e quindi quattro fasi insieme non possono coesistere. Non vi è insomma alcun punto quadruplo, come si vede nel diagramma.

Per quanto possa parere strano, però, anche l'acqua ha più fasi solide distinte. Infatti, se sottoposto a pressioni dell'ordine delle migliaia di atmosfere, i legami idrogeno tipici del ghiaccio tradizionale si schiacciano, il tutto ricristallizza con una struttura romboedrica e si forma una nuova fase solida chiamata ghiaccio II. Esso ha una densità maggiore di quella dell'acqua liquida, a differenza del ghiaccio I; ghiaccio I, ghiaccio II e acqua liquida possono coesistere in un punto triplo con temperatura T = 22°C e pressione P = 2100 atmosfere. In tutto oggi si conoscono ben 17 fasi solide dell'acqua, alcune con caratteristiche davvero esotiche e a pressioni veramente elevate!

Si osservi che la regola delle fasi giustifica la comparsa della sosta termica vista sopra. Siccome, quando coesistono due fasi, si ha v = 1, ne consegue che, fissata la pressione, io non posso variare nulla, neppure la temperatura. Se la vario, una delle due fasi sparisce. Ecco perchè, in transizione di fase, P e T restano costanti assieme. In questo caso si parla di trasformazione isotermobarica.

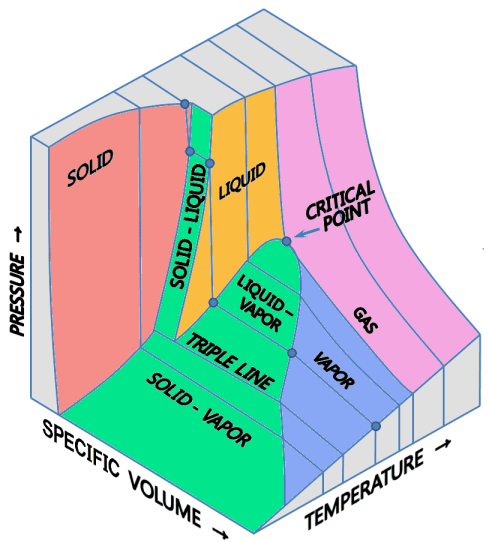
Non basta:C il 2 presente nella regola delle fasi indica semplicemente il numero di variabili con cui noi descriviamo il sistema: nel ostro caso, P e T. Se di variabili ne avessimo tre (P, V, T), la regola delle fasi diventerebbe v = c + 3 – f. Ma il diagramma delle fasi può essere tridimensionale? Sì, se si sfruttano tre assi coordinati anziché due: uno per il volume, uno per la pressione e uno per la temperatura assoluta. Il piano coordinato PV è quello di Clapeyron, quello PT è quello delle fasi. Nel diagramma così ottenuto, che potete vedere qui sopra, le diverse fasi sono rappresentate da porzioni di volume in tre dimensioni, perchè questa volta v = 3: in rosso la fase solida, in giallo la fase liquida, in blu la fase vapore, in porpora la fase di gas. Le superfici in verde rappresentano le zone di coesistenza tra le fasi, perchè v = 2, mentre la zona di coesistenza tra tre fasi è una linea, la linea tripla, perchè v = 1.

Aggiungiamo però due parole sul comportamento dei materiali amorfi come resine, polimeri, vetro, ceramica... Essi vengono sintetizzati generalmente allo stato liquido, per poi subire un processo di raffreddamento che ne evita la cristallizzazione: viene così mantenuta la tipica struttura microscopica disordinata del liquido, ma portandolo ai livelli di viscosità elevatissimi tipici di un solido. Prendiamo ad esempio il vetro: tipicamente amorfo, è uno dei primi materiali artificiali creati dall'uomo, forse scoperto come sottoprodotto della lavorazione dei metalli. Le qualità che associamo al vetro sono trasparenza, rigidità e fragilità, e nessuno, tranne un fisico, pensa che il vetro non sia un solido. Tuttavia, consideriamo un materiale che certamente non è un vetro, per esempio l'acqua. Quest'ultima a pressione ambiente rimane liquida tra 0° e 100°C, ma non appena abbassiamo la temperatura sotto lo zero diventa ghiaccio. Al punto di fusione, insomma, le proprietà dell'acqua cambiano bruscamente. Nei ruscelli di montagna l'acqua a una temperatura di poco superiore allo zero scorre verso valle proprio come d'estate: l'acqua resta liquida finche non ghiaccia diventando un solido piuttosto duro, così come il ghiaccio non diventa via via più molle prima di squagliarsi. Insomma, come si è visto sopra, tutti suddividiamo i materiali in solidi, liquidi e gassosi e sappiamo che passano da una fase all'altra in maniera istantanea quando si giunge alla temperatura di transizione di fase, ma in realtà siamo circondati da materiali che si comportano in maniera diversa, e il vetro è uno di questi.

Pensiamo a una candela accesa. Vicino alla fiamma la cera e un liquido perfetto che, se si rovescia la candela, cola senza problemi; quando pero comincia a scivolare giù lungo il bordo della candela, via via che scende si raffredda e cola sempre più lentamente fino al momento in cui "si blocca" perché la forza di gravità non ce la fa più a farla scemdere. Se interveniamo noi cercando di schiacciarla (possibilmente non con le dita per non scottarci), sentiamo che è assai cedevole e cambia forma senza la necessità di compiere grandi sforzi. Progressivamente però diventa sempre meno cedevole fino al punto in cui è a tutti gli effetti un solido. Ma se la cera prima era un liquido e poi è diventata un solido, quando e a quale temperatura è avvenuto il passaggio di stato? Difficile rispondere. Possiamo convenzionalmente introdurre una soglia di durezza e affermare che la cera diventa solida quando oltrepassa quella soglia, ma la temperatura precisa dipende dalla soglia scelta. In questa situazione la cera è un liquido sottoraffreddato e sotto una certa temperatura è un solido a tutu gli effetti e diventa quello the i fisici chiamano vetro. Lo stesso comportamento avviene per quello che noi chiamiamo comunemente con questa parola: da liquido quasi perfetto diventa un liquido viscoso e malleabile, un attimo fuggente (per dirla con l'omonimo film) durante il quale l'artigiano di Murano ne approfitta per realizzare le sue opere d'arte, ma anche in questo caso non si può individuare l'istante preciso in cui esso passa da liquido a solido. In pratica, i materiali amorfi sono metastabili, ovvero si trovano in uno stato intermedio tra il liquido e il solido, e sono soggetti a lenti cambiamenti strutturali, tali che nell’arco di milioni di anni essi compiono una vera e propria evoluzione verso configurazioni più stabili. A lungo è circolata la leggenda (eh sì, anche la Fisica ha le sue leggende) secondo cui le vetrate delle antiche cattedrali gotiche, risalenti al Medioevo, risultano essere più spesse sul fondo che in cima, e questo dimostrerebbe senza ombra di dubbio che il vetro è un liquido che scorre molto lentamente. In realtà si tratta solo di una leggenda metropolitana: non c’è mai stato uno studio scientifico in grado di dimostrare che quelle antiche vetrate sono più spesse nella parte inferiore; ma, anche se si rilevassero anomalie, la differenza di spessore non avrebbe nulla a che vedere con il fatto che il vetro sia un solido o un liquido, bensì sarebbe dovuta al fatto che il processo di lavorazione del vetro che veniva utilizzato all’epoca non era in grado di produrre lastre perfette con spessore uniforme. Conclusione: il vetro è un solido, anche se qualcuno preferisce l'espressione "falso solido", essendo privo di struttura cristallina.

.

A questo punto, sento già la vostra domanda: che differenza c'è mai, tra fase vapore e fase gas? A questa domanda risponderemo nel capitolo seguente. Per tornare all'indice, invece, il link è questo.

____