
Importante: per comprendere questo approfondimento è necessario conoscere i principi fondamentali della teoria elettromagnetica.
Nel paragrafo 2.1 abbiamo visto che la critica einsteiniana ai concetti di spazio, tempo e moto assoluti prese le mosse da alcune contraddizioni insite nella descrizione classica dei fenomeni elettrodinamici, e che la teoria dell'etere, giudicata da Maxwell indispensabile per giustificare la propagazione nel vuoto delle onde elettromagnetiche da lui previste; e proprio la teoria dell'etere divenne il cavallo di Troia che provocò la crisi della Teoria Classica dei Campi. Al termine di questa mia sintetica esposizione della Relatività Ristretta vorrei ritornare brevemente su quel problema per indicare, almeno in prima approssimazione, la traccia della sua soluzione.
La prima considerazione da fare consiste nel rilevare che quelle contraddizioni nascono solo perché si inquadrano i fenomeni cui esse si riferiscono nella cornice della Fisica Classica e perché, per descrivere il punto di vista di osservatori in moto relativo tra loro, si utilizzano le famose trasformazioni galileiane. Ma quei fenomeni, che appartengono all'ambito dell'elettromagnetismo, sono descritti dalle equazioni di Maxwell, e queste mantengono invariata la loro forma solo quando, per esprimerle in due sistemi di riferimento in moto relativo, si utilizzano le trasformazioni di Lorentz e non quelle di Galileo.
Se dunque due osservatori O1 e O2, solidali a due sistemi di riferimento K1 e K2 in moto rettilineo uniforme l'uno rispetto all'altro, vogliono descrivere un fenomeno elettromagnetico senza giungere a esiti contraddittori (mediante i quali si potrebbe giungere a stabilire chi è fermo e chi è in moto, contro il primo dei due postulati di Einstein), dovranno applicare alle grandezze che descrivono il fenomeno in uno dei due sistemi di riferimento le trasformazioni di Lorentz onde ottenere la descrizione del fenomeno nell'altro sistema di riferimento. Esemplificheremo ora gli esiti dell'applicazione delle trasformazioni galileiane ai fenomeni elettromagnetici in un caso particolare, calcolando la forza prodotta su una carica elettrica da una fila di cariche elettriche in quiete e in moto secondo la relatività galileiana e secondo quella einsteiniana.

Si consideri dunque la distribuzione filiforme ed indefinita di cariche positive di figura 1, ed una carica q posta a distanza r da essa. Per un osservatore O solidale con tale distribuzione di cariche, su q agirà una forza repulsiva Fc calcolabile applicando le consuete leggi dell'elettrostatica. Come sappiamo, l'espressione di questa forza è:
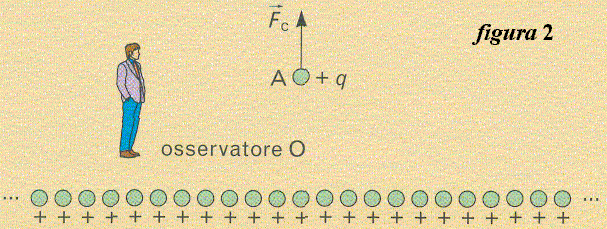
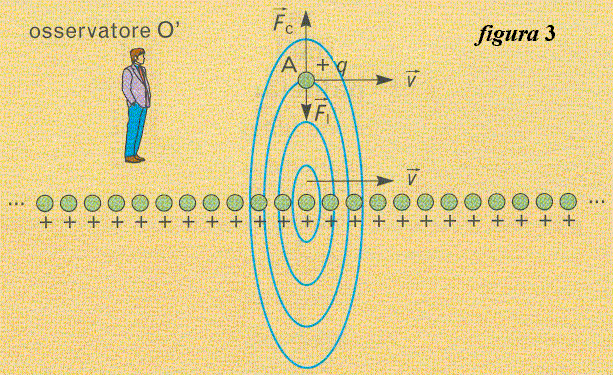
dove con λ si è indicata la densità lineare di carica, cioè la carica distribuita su un segmento della fila di cariche, divisa per la lunghezza del segmento stesso (si misura dunque in A / m). Proviamo ora a determinare la forza agente sulla carica q, ragionando dal punto di vista di un osservatore O' che si muove rispetto alla fila di cariche - e, quindi, anche rispetto alla carica q - con una velocità v diretta verso sinistra. Dal suo punto di vista, q e la fila di cariche si muoveranno verso destra con velocità v (vedi figura 3) e, quindi, ragionando in termini non relativistici, le sue previsioni riguardanti il valore della forza agente su q saranno le seguenti:
a) su q deve agire una forza coulombiana, centrifuga rispetto alla fila di cariche, data dalla formula (5.2) precedentemente scritta;
b) su q deve agire anche una forza di Lorentz diretta verso la fila di cariche, e data da F1 = q v B, essendo B il modulo del campo magnetico generato dalla fila di cariche.Il valore di B può essere dedotto trattando la fila di cariche come una corrente di intensità i data da:
![]()
N è il numero di cariche presenti nel tratto di lunghezza pari a v Δt. Indicando allora con n il numero di cariche per unità di lunghezza, la precedente ci fornisce:
![]()
Ma q n è ciò che abbiamo denominato densità lineare di carica (λ), e perciò i = λ n. In conclusione, applicando la legge di Biot-Savart alla nostra fila di cariche abbiamo:
![]()
da cui:
![]()
Poiché µ0 è legato alla costante dielettrica ε0 dalla relazione (1.3), la formula precedente diviene:
Combiniamo allora la (5.2) e la (5.3) e troviamo che, per l'osservatore O', la forza agente sulla carica q deve valere:
Questo risultato, nettamente diverso da quello previsto da O, è decisamente in contrasto con il primo postulato di Einstein, perché in tal caso potremmo finalmente decidere, osservando il comparire o lo scomparire della forza magnetica, chi fra O e O' si muove e chi sta fermo! Dove sta il busillis?
Semplice: tutto il nostro ragionamento si è basato, ancora una volta, sui principi della relatività galileiana. Completamente diverse sarebbero state le conclusioni riguardanti le osservazioni di O e O' se avessimo ragionato utilizzando i principi della relatività einsteiniana, tenendo conto, cioè, della dilatazione dei tempi e della contrazione delle lunghezze, che influenzano le grandezze fisiche coinvolte in un qualunque fenomeno che si sviluppa in un sistema in movimento. In tal caso infatti i due osservatori avrebbero misurato, ciascuno nel proprio sistema di riferimento, la medesima variazione della quantità di moto della carica q, e non avrebbero quindi potuto dire nulla in assoluto sul proprio stato di moto.
Per dare una giustificazione, pur approssimata, della identità di vedute dei due osservatori O e O' delle figure 1 e 2 relativamente al comportamento dinamico della carie q situata in prossimità della fila di cariche, anch'esse positive, si osservi che, nel considerare la densità lineare di carica, non abbiamo stabilito alcuna differenza fra quella misurata da O e quella misurata da O'. Ma, da un punto di vista relativistico, ciò è un errore: se infatti per l'osservatore O, fermo rispetto alla fila di cariche, N Cariche sono contenute in un segmento di lunghezza L, l'osservatore O', che vede quello stesso segmento muoversi con velocità v, dirà che quelle N cariche sono contenute in un segmento di lunghezza pari a:
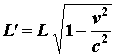
per via della (2.1). Di conseguenza, se la densità lineare di carica per O vale λ, per O' essa vale (mi si perdoni il gioco di parole):
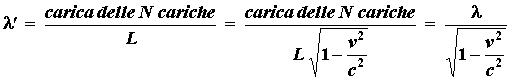
Si noti che, nella considerazione svolta per dedurre la relazione fra λ e λ', si è implicitamente assunto che il valore delle cariche non dipenda dal sistema di riferimento. Questa assunzione si fonda essenzialmente sul dato sperimentale che lo stato elettrico di qualunque sistema si rivela indipendente dal suo stato di moto.
Passiamo ora alla determinazione della variazione della quantità di moto Δp prodotta sulla carica q dalla forza generata dalla fila di cariche dei sistemi di riferimento ai quali appartengono O ed O'. Per i due sistemi di riferimento si avrà rispettivamente Δp = F Δt e Δp' = F Δt'. Tenendo conto che il tempo proprio è quello dell'osservatore rispetto al quale il sistema di cariche è in quiete, le due quantità Δt e Δt' sono legate tra di loro dalla relazione (2.1):
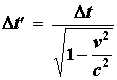
Tornando alle variazioni delle quantità di moto avremo allora, utilizzando le formule (5.2) e (5.4):
per
l'osservatore
O :

per
l'osservatore O' :
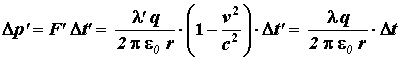
Come si vede, dunque, le constatazioni dei due osservatori riguardanti la dinamica della carica q sono ora perfettamente equivalenti.
Un'analisi più generale del modo con il quale le componenti del campo elettrico e del campo di induzione magnetica si trasformano nel passaggio da un sistema di riferimento ad un altro (in moto rettilineo ed uniforme rispetto ad esso, si intende) dimostra che i due campi non possono più essere considerati come enti indipendenti e separati, ma devono essere considerati come appartenenti a un più generale ente fisico, la cui descrizione richiede lo sviluppo di un formalismo matematico in uno spazio quadridimensionale: il cronotopo di Minkowsky, appunto.
Quest'affermazione può essere meglio compresa se si deducono le cosiddette trasformazioni di Lorentz per il campo magnetico, cioè quelle che permettono di mettere in relazione le componenti dei campi elettrici e magnetici misurati dai due osservatori K e K'. Supponiamo che essi siano in moto relativo rettilineo uniforme lungo l'asse x con velocità v, e che vi siano due cariche q e Q solidali con le origini dei due sistemi di riferimento. Entrambi gli osservatori attribuiscono alle cariche gli stessi valori, per quanto detto sopra; per l'osservatore K' vi è solo l'interazione elettrica tra q e Q, e la forza misurata su q è F' = q E', dove E' è il campo elettrico prodotto da Q e misurato da K'. Ma K vede la carica Q in moto, dunque egli osserva che essa produce sia un campo elettrico E che un campo magnetico B. Ma anche q è vista in moto con velocità v, per cui la forza esercitata da Q su q e misurata da K è F = q E + q v x B. Se Ex, Ey, Ez sono le componenti di E viste da K, Bx, By, Bz sono le componenti di B viste da K, Ex', Ey', Ez' sono le componenti di E viste da K', e Bx', By', Bz' sono le componenti di B viste da K', le leggi di composizione risultano le seguenti:
|
|
In modo analogo si ricavano le trasformazioni inverse.
Queste trasformazioni provano definitivamente che il campo elettrico ed il campo magnetico non rappresentano due entità fisiche separate, ma sono due aspetti diversi di una stessa realtà fisica, chiamata campo elettromagnetico: infatti, passando da un sistema di riferimento all'altro, le componenti del campo elettrico dipendono anche da quelle del campo magnetico, e viceversa. La separazione di un campo magnetico nelle sue componenti elettriche e magnetiche non è un fatto assoluto, bensì dipende dal moto delle cariche relativamente all'osservatore. E questo conferma la necessità di ricorrere alle trasformazioni di Lorentz per conservare la covarianza delle equazioni elettromagnetiche.
A questo punto però sorge un ultimo dubbio. Il campo elettrico ed il campo magnetico hanno globalmente sei componenti scalari, e cioè Ex, Ey, Ez, Bx, By, Bz; dunque il campo elettromagnetico non può essere certo un vettore, avendo sei componenti! Sono troppe anche per il cronotopo. Infatti si dice il campo elettromagnetico, indicato di solito con T, ha natura tensoriale. Un tensore tridimensionale ha nove componenti, ed il tensore elettromagnetico è fatto così:
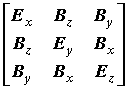
Come si vede, le componenti di E sono sulla diagonale principale, mentre quelle di B si trovano al di fuori di essa e sono disposte simmetricamente; infatti il campo magnetico è sempre perpendicolare al campo elettrico. La corretta formulazione della Relatività di Einstein (specialmente di quella Generale) è interamente di natura tensoriale. Ma per questo rimando il lettore ai testi specializzati citati nella Bibliografia.