Le scoperte di Einstein crearono un fermento mai visto da secoli. La rivoluzione da lui operata era pari a quella copernicana: ora l'universo andava visto in un modo affatto nuovo.
Certo, quando si viaggia in automobile ad una velocità di "soli" 144 Km / h , sette milioni e mezzo di volte più piccola di quella della luce, la percezione del tempo o le misure lineari delle persone a bordo non cambiano in modo apprezzabile, ma se si costruisce un sincrotrone per lo studio delle particelle subatomiche si deve tenerne ben conto!
Per descrivere le differenze nel moto dovute alla dilatazione dei tempi e alla contrazione delle lunghezze si deve ricorrere ad un nuovo sistema di coordinate. Il vecchio sistema galileiano, basato su lunghezze e tempi assoluti, era assai semplice ma, come questa unità cercherà di mostrare, assolutamente inadatto a descrivere i fenomeni studiati dalla meccanica relativistica.
Consideriamo un sistema di assi cartesiani ortogonali, ed un altro che si sposta rispetto ad esso con velocità costante v in modo che gli assi x e x' coincidano scivolando l'uno sull'altro, e gli altri (y e y', z e z') restino paralleli fra di loro, e consideriamo i due diversi sistemi di coordinate:
K (x, y, z, t) e K' (x', y', z', t')
riferiti rispettivamente alle origini O e O', come abbiamo già fatto nel paragrafo 0.1. Se K' si muove rispetto a K con velocità v, per la contrazione delle lunghezze sarà:
O'P'
![]() (3.1)
(3.1)
Infatti, considerando in K un punto P dell'asse x = x', punto che corrisponde a P' nel sistema K', le sue coordinate rispetto ai due sistemi risulteranno:
P (x, 0, 0, t) e P' (x', 0, 0, t')
O'P' = x' se K' é fermo, perché se é in moto con velocità v esso si contrae nella direzione del moto riducendosi ad una lunghezza data dalla (3.1).
Ma essendo O'P' = OP – OO' = x – v t , si deduce che
![]()
da cui:
Ordinata e quota rimangono uguali, visto il modo in cui K' si muove rispetto a K. Si consideri invece la coordinata temporale. Il segmento OP rispetto al sistema K' é uguale alla somma di:
OO' = v t con O'P = O'P' = x'
Il segmento OP, però, se K' fosse fermo, misurerebbe x; in effetti si muove con velocità v, e dunque, nella direzione del moto, risulta più corto:
quindi:
![]()
e, utilizzando la (3.2):
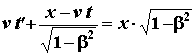
moltiplicando ambi i membri per ![]() ho:
ho:
![]()
da cui si ricava, senza alcuna difficoltà:
Si hanno così le nuove trasformazioni chiamate TRASFORMAZIONI DI LORENTZ, in onore di H.A.Lorentz, lo scienziato olandese da noi già citato nelle unità precedenti:
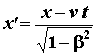
y' = y z' = z
|
Se v
é molto vicino a zero, cioé se v <<
c, si ritorna alle trasformazioni classiche di Galileo (0.1), perché
![]() e
e
![]() .
.
Le formule inverse si ottengono senza calcoli, solo tenendo conto che, se K' si considera fisso, sarà K a muoversi con una velocità – v ; allora ad x si deve sostituire x' e t' a t. Si ha così:
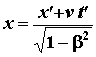
y = y' z = z'
|
Strano destino, quello della relatività ristretta: nascere, svilupparsi e giungere a scoperte allucinanti, tali da squassare dalle fondamenta tutto il grattacielo innalzato da Galilei e Newton, solo per giustificare qualcosa che era già acquisito da decenni come le equazioni di Mawxell. Un destino simile a quello dei partecipanti alla Corsa della Regina Rossa in "Alice nel Paese delle Meraviglie" di Lewis Carroll: correre, correre per restare al punto di partenza...

Adesso tocca alla composizione einsteiniana delle velocità. Chi vuole impararla passi subito al paragrafo successivo.