
Il primo mito sfatato da Einstein fu quello del tempo assoluto. Uno dei cardini della fisica classica era la contemporaneità degli eventi fisici rispetto a tutti i sistemi di riferimento; Einstein dimostrò illusorio questo principio con il ragionamento dell'orologio a luce.
Si dice « orologio a luce » quello che calcola il tempo attraverso la riflessione di un raggio di luce fra due specchi piani e paralleli. Dati due simili orologi in quiete, ben sincronizzati, la partenza dei raggi di luce, la loro riflessione e la loro percezione saranno eventi contemporanei. Ma se uno si muove di moto relativo rispetto all'altro, con velocità uniforme v, che cosa accade?

Per l'osservatore solidale con l'orologio in moto relativo, diciamo nel sistema K', il raggio di luce continua a riflettersi fra i due specchi, perpendicolarmente ad essi. Ma per un osservatore del sistema K , solidale con l'orologio che per noi é in quiete, il moto del raggio di luce si compone con quello traslatorio dell'orologio, e si ha la traiettoria diagonale della figura: non più AB, ma A'B'' e B''A'''. Ora, sia t il tempo misurato dall'orologio a luce in K per percorrere il tratto AB, e t' il tempo misurato in K' per percorrere uno spazio uguale. É chiaro che t < t', essendo AB = A''B'' < A'B'' (il cateto é minore dell'ipotenusa); ed essendo la velocità della luce costante in ogni sistema di riferimento, risulta:
per il teorema di Pitagora:
Da cui:
c 2 t' 2 = c 2 t 2 + v 2 t' 2
cioè:
( c2 – v2 ) t' 2 = c 2 t 2
con facili passaggi algebrici, si ricava:
Condizione di realtà é che sia:
![]()
Il denominatore é sempre minore di uno, quindi l'intervallo di tempo tempo misurato nel sistema K' é sempre maggiore di quello misurato nel sistema K fra due eventi apparentemente contemporanei, come si vede in figura. Per l'orologio in moto, insomma, il tempo passa più lentamente. É questo il fenomeno noto come DILATAZIONE DEI TEMPI. É come se i nostri due sistemi di riferimento vivessero in due... tempi differenti.

Naturalmente, se gli intervalli di tempo visti da due osservatori diversi risultano differenti, va all'aria anche il concetto di simultaneità tra eventi; per questo cedo la parola ad Einstein stesso, rimandandovi alla Lettura 2 dedicata a quest'argomento.
Facciamo un esempio. Sul treno di Einstein il tempo scorre più lentamente: se al passaggio da una stazione il suo orologio viene accordato con quello sulla pensilina, dopo un'ora ci si accorge che, al passaggio ad una nuova stazione, l'orologio di questa segna che é trascorsa più di un'ora, e precisamente:
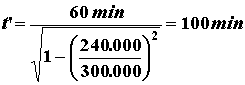
A questo punto sorge spontanea una domanda: la dilatazione relativistica dei tempi é una realtà fisica o una mera astrazione matematica? In effetti è più reale di quanto non si creda in quanto, senza di essa, spiegare taluni fenomeni é impossibile. Un esempio? Si prenda il caso dei mesoni µ, detti MUONI, prodotti naturalmente nell'alta atmosfera dallo scontro di particelle del vento solare con i nuclei degli atomi di gas rarefatti. Come? Anzitutto vengono prodotti dei PIONI, mesoni molto comuni, secondo la reazione:
![]()
Nella figura seguente è possibile vedere questa reazione, fotografata
in camera a nebbia. In circa 10 secondi, il pione negativo decade in un muone e
in un antineutrino muonico ![]() , un
leptone "compagno" del muone di cui si sa ancora pochissimo:
, un
leptone "compagno" del muone di cui si sa ancora pochissimo:
![]()
La vita media dei muoni é molto bassa, circa 2,2 microsecondi, assai minore del tempo necessario per giungere sulla superficie terrestre. Eppure, si riesce a rivelare un gran numero di muoni che riescono a raggiungere la bassa troposfera. Come mai?
Una sola spiegazione è possibile: grazie alla dilatazione dei tempi, la loro vita media si é ALLUNGATA! Ma, da buoni studenti di Relatività, potete fornire una descrizione del fenomeno dal punto di vista dei muoni stessi, ed affermare che essi vedono la Terra venire loro incontro ad una velocità prossima a quella della luce, il che comporta una... contrazione delle sue dimensioni, e quindi anche della loro distanza dal suolo, come apprenderemo nel paragrafo 2.4!

A questo punto è possibile comprendere perché ho dedicato quest'unità a Dante e Marco Lombardo, i quali, apparentemente, con Einstein non hanno proprio nulla a che fare. Chi ha studiato con attenzione la Divina Commedia dovrebbe ricordare le parole che Marco Lombardo rivolge a Dante nel canto XVI del Purgatorio (vv. 25-27):
« Or tu chi sé, che il nostro fumo fendi,
e di noi parli pur, come se tue
partissi ancor lo tempo per calendi? »
I due personaggi, Dante e l'anima purgante, vivono in due tempi diversi: l'uno nella dimensione terrena, con un preciso limite per la propria vita, l'altro proiettato nella dimensione della eternità. Le cose viste da loro sono le stesse, ma misurate in due modi differenti. Dante, come si vede, è stato così geniale da anticipare persino Einstein e la relatività dei tempi...

Così Gustave Dorè immaginò l'incontro fra Dante, Virgilio e Marco Lombardo
Nel successivo paragrafo 2.3 faremo una pausa tra tante formule, perché ci divertiremo ad analizzare il paradosso dei gemelli; le formule spunteranno fuori di nuovo nel paragrafo 2.4, nel quale vedremo come Einstein ha demolito, dopo il tempo assoluto, anche l'immutabilità delle lunghezze.