5.2   Un cono a... quattro dimensioni

Ritornando al concetto di spazio tetradimensionale, esso é perfettamente analogo a quelli mono-, bi- e tridimensionali, con l'unica differenza che la coordinata tempo é differente qualitativamente (non quantitativamente) dalle coordinate spazizli. Minkowski, genialmente, oltre ad x, y e z introdusse la coordinata i c t , dove c é la velocità della luce ed  é l'unità immaginaria, in modo da rendere le coordinate omogenee. Infatti moltiplicando c e t ho uno spazio, e quindi questa nuova coordinata ha le stesse dimensioni fisiche di x, y, z.

Ora, la distanza di due punti A(x_A) e B(x_B) in uno spazio monodimensionale é:

quella di due punti A( x_A ; y_A ) e B( x_B ; y_B ) in uno bidimensionale é:

quella di due punti A( x_A ; y_A ; z_A ) e B( x_B ; y_B ; z_B ) in uno tridimensionale é

In uno quadridimensionale, utilizzando la quarta coordinata tempo così come é stato introdotta da Minkowski, poiché i² = – 1, si ha che:

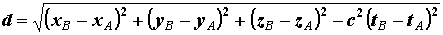
Questa distanza viene chiamata intervallo invariante. Infatti, mediante le formule relativistiche della dilatazione dei tempi e della contrazione delle lunghezze, si può dimostrare che, qualunque sia il sistema di riferimento, la distanza di due eventi nello spazio - tempo é la stessa, ed è pari a:

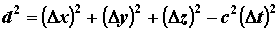
Insomma, passando da un sistena di riferimento a un altro, cambiano le componenti del vettore quadridimensionale AB corrispondente alla distanza di due eventi A( x_A ; y_A ; z_A ; i c t_A ) e B( x_B ; y_B ; z_B ; i c t_B ), ma il modulo di tale vettore, cioè la distanza d tra i due eventi nello spazio - tempo è sempre la stessa!

Nello spazio della geometria euclidea in cui viviamo, la distanza al quadrato tra due punti può essere solo positiva, se i due punti sono distinti, o nulla, se essi sono coincidenti. In nessun caso d² può essere negativo. Invece, la formula appena scritta ci dice che d² può avere anche segno meno! I casi allora possono essere non due, ma tre:

1) Se d² > 0, si dice che quello che separa i due eventi è un intervallo di tipo tempo; in questo caso un segnale emesso al tempo t_A in corrispondenza dell'evento A può propagarsi fino a influenzare, al tempo t_B, l'evento B: quindi l'istante di tempo t_A precede l'istante di tempo t_B in tutti i sistemi di riferimento. Inoltre, esiste sempre un sistema di riferimento inerziale (cioè solidale con il fenomeno osservato) in cui i due eventi hanno le stesse coordinate spaziali.

2) Se invece d² < 0, si dice che quello che separa i due eventi è un intervallo di tipo spazio; in questo caso un segnale emesso in corrispondenza dell'evento A non può propagarsi fino ad influenzare l'evento B, quindi i due eventi sono causalmente indipendenti in tutti i sistemi di riferimento. Inoltre, esiste sempre un sistema di riferimento inerziale in cui i due eventi hanno le stesse coordinate temporali.

3) Se infine d² = 0, si dice che quello che separa i due eventi è un intervallo di tipo luce; in questo caso, Δx = c Δt, e quindi solo un segnale luminoso che parte dall'evento A può propagarsi nel vuoto fino ad influenzare l'evento B.

Rappresentare il sistema tetradimensionale ( x, y, z, i c t ) é piuttosto difficoltoso; conviene di più, anche alla luce delle trasformazioni di Lorentz, rappresentare il sistema bidimensionale ( x, i c t ). Questo piano prende il nome di CRONOTOPO, dal greco "spazio-tempo". In questo sistema, le rette parallele all'asse x uniscono eventi contemporanei che prendono posto in luoghi diversi, mentre quelle parallele all'asse i c t costituiscono una successione cronologica di eventi che prendono posto nel medesimo luogo. Tutte le rette passanti per l'origine degli assi costituiscono una successione di eventi che si spostano linearmente nello spazio e nel tempo, cioè di moto uniforme. Le curve passanti per l'origine sono invece successioni di eventi più generali.

Ci si accorge subito di qualcosa di importantissomo: in questo sistema di coordinate, la distanza di due eventi può essere nulla anche quando essi non coincidono! Infatti, se:

la distanza dall'origine risulta:

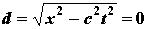
Rappresentando le due rette di equazioni , si divide il nostro piano in due parti di uguale ampiezza:

Nella zona colorata in azzurro nel primo e nel secondo quadrante, risulta subito:

    (5.1)

Poiché, a meno del fattore ± i , c t rappresenta la distanza percorsa dalla luce nell'intervallo di tempo che separa l'evento considerato dall'origine dei tempi, questo evento può essere raggiunto da un raggio di luce che parta dall'origine. La stessa relazione vale anche nella zona colorata in azzurro nel terzo e quarto quadrante, quindi l'origine può essere raggiunta da un raggio di luce che parte dall'evento considerato. Quest'ultima si chiama perciò la ZONA DEL PASSATO, l'altra la ZONA DEL FUTURO. L'origine costituisce il PRESENTE, quando x = 0 e t = 0. Le altre due zone grige sono invece caratterizzate dal fatto che

quindi la distanza x é maggiore di quella che la luce può percorrere nel tempo t. Tali punti risultano IRRAGGIUNGIBILI  dall'origine (primo e secondo quadrante), o l'origine é irraggiungibile partendo da essi (terzo e quarto quadrante). Essi costituiscono tutti gli eventi che non possono influenzare o essere influenzati dal momento presente. In sostanza, ogni individuo nella sua vita percorre una linea che viene dal PASSATO, attraversa il PRESENTE (l'origine), e sfocia nel FUTURO. Arresti o dietrofront non sono ammessi. Si può percorrere solo una ben determinata, continua e crescente LINEA DI UNIVERSO.

Ecco un esempio. La stella Alfa  Centauri è posta a 4,3 anni luce dalla terra; ciò significa che, se invia al momento presente un raggio di luce nella nostra direzione, lo si vedrà solo fra 4,3 anni, e se noi inviamo un raggio di luce verso Alfa Centauri, essa attenderà 4,3 anni prima di vederlo. Se per ipotesi io fossi fidanzato con una ragazza di Alfa Centauri, e venissi a sapere che essa si sposerà tra 10 anni con un altro, io potrei raggiungere l'astro e mandare a monte le nozze, perché viaggiando alla velocità della luce ci metterei "solo" 4,3 anni luce; potrei farcela anche viaggiando su un razzo stile "bambola russa" che si avvicini alla fatidica velocità c pur senza raggiungerla. Se invece lo sciagurato matrimonio avvenisse tra soli 4,3 anni, l'unico modo che avrei a disposizione per non perdere la morosa è quello di puntare un raggio Laser collimatissimo contro la prima stella del Centauro, ed usarlo per incenerire il mio rivale d'amore proprio davanti all'altare, perché solo la luce può percorrere 4,3 anni luce in 4,3 anni. Ma io non potrei fare nulla se le nozze avvenissero solo tra 2 anni, perché neppure la luce sarebbe abbastanza veloce per riuscirci, ed Einstein mi proibisce di andare più svelto. Quell'evento é fuori dalla mia portata perché é anche fuori dalla portata della luce.

La zona colorata nella figura precedente prende il nome di CONO DI LUCE. Infatti, introducendo la coordinata y, esso assume la forma di un doppio cono, così (immagine tratta da S.Hawking, Dal Big Bang ai Buchi Neri, [ 11 ]):

In questo caso il cono inferiore rappresenta il passato, il cono superiore rappresenta il futuro.

Introducendo anche la terza coordinata z, il cono diventa un IPERCONO in quattro dimensioni, non intuibile visivamente, perché il nostro cervello riesce a figurarsi al massimo oggetti in tre dimensioni.

Per ogni evento dello spazio-tempo possiamo costruire un cono di luce. Ogni linea di universo che attraversa l'interno del cono (o ipercono) di luce senza mai fuoriuscirne è permessa, come si è detto nel paragrafo 4.4, ad oggetti dotati di massa; le linee di universo contenute interamente nella superficie laterale del cono sono permesse ai raggi di luce, ma proibite per noi; le linee di universo che si trovano al di fuori del cono (quelle percorse dall'ipotetica Enterprise di capitan Kirk, per capirci) sono proibite per tutti. Poiché (secondo postulato di Einstein) la velocità della luce è la stessa per ogni osservatore, tutti i coni di luce saranno IDENTICI e puntati nella stessa direzione. Il PASSATO, il FUTURO e il CONO DI LUCE sono detti INVARIANTI DELLO SPAZIO - TEMPO, perché non cambiano qualunque sia il sistema di riferimento adottato.

A questo punto potete tornare al simulatore relativistico del dottor de Riso, e provare a quale velocità dovrete raggiungere con la vostra astronave (se mai avrete la fortuna di diventare capitani della Flotta Stellare) per poter viaggiare in pochi giorni, ore o minuti verso una data futura; oppure potete passare alla lettura dedicata alla Freccia del Tempo; oppure potete accedere all'approfondimento 3, nel quale verrà mostrato come il campo magnetico trova una naturale collocazione all'interno del cronotopo, anziché dello spazio-tempo newtoniano (attenzione, però: tale approfondimento è riservato a chi ha già studiato il magnetismo in generale e la forza di Lorentz in particolare). Per chi non riesce a resistere alla tentazione di conoscere per sommi capi i contenuti della Relatività Generale, ho preparato l'approfondimento 4. Infine, se vi sentite pronti, potete cimentarvi con i test di quest'unità, prima di osare inoltrarvi nel test finale. In bocca al lupo!