4.4 Particelle senza massa

In base alla teoria dell'espansione delle masse, anche le espressioni della quantità di moto p e dell' energia totale E_tot risultano modificate. D'ora in poi si seguirà la consuetudine di porre  ; estendendo inoltre la definizione classica  p = m v mediante la (4.1), si ha:

  (4.3)

La (4.3) può essere verificata sperimentalmente: basta misurare la quantità di moto di una particella accelerata in un sincrotrone. Ed ecco i risultati sperimentali ottenuti da W.Kauffman nel 1901 (cerchietti bianchi), da A.Bucherer nel 1909 (cerchietti neri) e da C.Guye e C.Lavanchy nel 1915 (le crocette). La figura è tratta da un'edizione d'epoca di Scientific American:

Si noti come il grafico soprastante sia sostanzialmente identico a quello del paragrafo 4.2, giacché entrambi, in buona sostanza, rappresentano il rapporto  in funzione di v/c !

In effetti, soltanto per velocità molto grandi si verifica una notevole differenza della quantità di moto della particella rispetto al valore m₀ v previsto dalla meccanica newtoniana: se v = c / 2, si ha solo p / m₀ v = 1,15, cioè l'aumento relativistico della quantità di moto è appena del 15 %. Per piccole velocità (v << c) si può ritenere  , e la (4.3) coincide con l'espressione classica della quantità di moto. Questo dimostra che la Fisica Classica non è tutta da buttar via, ma rappresenta un'approssimazione della Fisica Relativistica, valida a basse velocità.

Quanto poi all'energia, si dimostra che si può scrivere:

  (4.4)

la dimostrazione richiede il calcolo integrale, e verrà trattata nell'Approfondimento 2. La (4.4) ci dice che, per v = 0, l'energia non è zero, come risulterebbe dall'espressione classica dell'energia cinetica, bensì m₀ c², cioè l'energia a riposo del corpo. Al crescere di v il denominatore tende a zero, per cui l'energia cresce indefinitamente, e ciò giustifica il nome di dinamica delle alte energie che viene solitamente dato all'argomento dell'unità 4. Si noti che, nel modello newtoniano, a velocità c una particella avrebbe un'energia cinetica finita m₀ c²/2, mentre nel modello einsteiniano a velocità c l'energia diventa infinita, sulla scorta della dilatazione della massa. E ciò non fa altro che confermare l'illusorietà della speranza dell'Enterprise di capitan Kirk di raggiungere o addirittura superare la velocità della luce.

Dalla (4.3) si può ricavare v² :

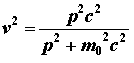
che, sostituita nella (4.4), dopo varie semplificazioni algebriche fornisce:

Essa permette di trovare l'energia totale in funzione della massa a riposo m₀ e della quantità di moto Q della particella. Se in particolare m₀ = 0 si ha: 

quindi, un'ipotetica particella senza massa può ancora avere una certa quantità di moto, contrariamente a quanto sostiene la Fisica Classica! Ma esistono particelle senza massa?

Certamente. É il caso del fotone, il "quanto" che trasporta l'energia delle onde elettromagnetiche, anch'esso previsto da Einstein nei suoi lavori sull'effetto fotoelettrico (1905). Secondo Einstein, esso é totalmente privo di massa a riposo, ma gli si deve associare un'energia pari a:

E  =  h f   (4.6)

dove f é la frequenza dell'onda elettromagnetica ed h la costante di Planck:

h = 6.67 * 10^–34 J s

Perciò, nonostante esso sia totalmente privo di massa a riposo (nel senso che non può neppure aver senso parlare di un fotone "a riposo"), ad esso si associa anche una quantità di moto:

e quindi una massa dinamica:

  (4.7)

Di altre particelle si suppone abbiano massa nulla. Vi é per esempio il gravitone, non ancora osservato, ma previsto dalle teorie dei campi come presunto mediatore del campo gravitazionale. Ci sono i neutrini, di cui si discute da decenni se abbiano massa nulla o non nulla. E lo zoo delle particelle a massa zero non finisce certo qui.

Chiudiamo con un'ultima osservazione. Se la luce è "fatta" di fotoni, si presuppone che essi possano viaggiare alla velocità della luce. Anzi, siccome è impossibile far « rallentare » la luce in base ai postulati di Einstein, è evidente che i fotoni possano viaggiare solo alla velocità della luce. Questo non è in contrasto con la nostra affermazione circa l'irraggiungibilità della velocità della luce? No, proprio perché il fotone ha massa a riposo nulla. Solo per una particella dotata di massa a riposo vige il divieto di uguagliare c, giacché altrimenti la (4.4) richiederebbe un'energia infinita per riuscirci. Per questo le particelle in natura si possono distinguere in due famiglie:

·      di massa a riposo nulla, che si possono muovere solo alla velocità della luce;

·      di massa a riposo non nulla (bradioni), che possono avvicinarsi a c senza mai raggiungerla.

Secondo alcuni esistono anche delle particelle (tachioni) che possono muoversi solo a velocità superiore a quella della luce, senza mai rallentare al di sotto di essa. Ciò è mai possibile? Sì, ma solo se esse hanno massa a riposo immaginaria (il che vuol dire che NON esistono a riposo). I tachioni sono un classico della fantascienza: nel film "I Fantastici Quattro e Silver Surfer" (2007), Mister Fantastic utilizza un raggio di tachioni per separare Silver Surfer dalla sua tavola, e nell’universo di Star Trek i tachioni sono frequentemente invocati per spiegare il funzionamento del dispositivo di occultamento dei Romulani, e proprio attraverso l'emissione residua di tachioni nel film "Star Trek, Nemesi" (2002) è possibile individuare un'astronave occultata. Nessuno però è mai riuscito finora ad identificare davvero dei tachioni: gli studenti di Fisica sappiano che c'è un Nobel che li aspetta, casomai un giorno fossero proprio loro a riuscirci!

E non è tutto: come ha scritto Davide Simonetti, « è plausibile pensare che così come accelerando il nostro tempo rallenta fino a fermarsi al raggiungimento (impossibile) di "c", particelle che nascono con velocità maggiore di quella della luce  viaggino, secondo il nostro punto di osservazione, a ritroso nel tempo? Se ciò fosse vero, non verrebbe violato il principio di casualità? E come sarebbe possibile che qualcosa torni ad un tempo che ormai non esiste più, o che qualcosa venga a visitarci da un tempo che non c'è ancora? » Domande per ora senza risposta, ma che come si vede qui sotto sono state ampiamente sfruttate da romanzi e fumetti di fantascienza!

Prima di chiudere questo capitolo, dobbiamo affrontare uno spinoso problema che, a fine 2011, minò la credibilità dell'intero edificio della Relatività Ristretta. È proprio vero che esistono particelle privilegiate, in grado esse sole di viaggiare più veloci della luce? Discuteremo la questione nel paragrafo 4.5.