4.2 La massa è energia

L'espansione delle masse porta a conclusioni sorprendenti. Anzitutto, la condizione di esistenza dell'espressione che fornisce il valore di m' é:

Se in particolare v tende ad avvicinarsi a c:

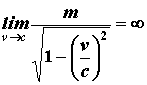
Ciò vuol dire che le velocità non possono crescere all'infinito. Secondo la fisica classica ciò era possibile; invece, a partire da Einstein, la velocità della luce diviene INSUPERABILE.

Crollano così i sogni di poter costruire fantascientifiche astronavi in grado di macinare anni luce al secondo: un corpo potrà avvicinarsi alla velocità della luce, ma mai uguagliarla. Inoltre, ad altissime velocità andare più veloce risulta difficile. Infatti, la massa cresce sempre di più, e più un corpo é massiccio, più energia si dovrebbe fornire per imprimergli una certa velocità. Il Secondo Principio della Dinamica asserisce che applicando una forza F ad un corpo, essa gli imprime una accelerazione a. Secondo Newton al crescere di F, anche a doveva crescere indefinitamente. Invece, ad un certo punto, l'energia fornita dalla forza applicata, invece di produrre ulteriore accelerazione, SI RIVERSA NELLA MASSA.

É per questo che, accelerando un corpo, apparentemente si "crea" materia, contro il principio di Lavoisier. In realtà non vi é nessuna creazione: semplicemente, é l'energia fornita al corpo che si trasforma in massa. Fu proprio tale considerazione che  condusse Einstein alla sua più grande scoperta. Vediamo come.

Si consideri il prodotto . Operiamo su di esso nel modo seguente:

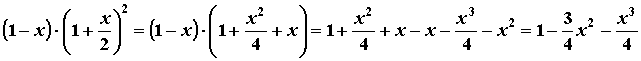
Se x << 1 (cioé x é molto minore di 1), x² e x³ sono trascurabili. Si ha quindi:

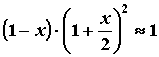
cioè, con facili passaggi algebrici:

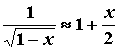
Se si usa la sostituzione , si ottiene:

dove m₀ é la massa a riposo del corpo, calcolata quando la sua velocità rispetto all'osservatore è zero, mentre m_d é la sua massa dinamica, a velocità v. Se si moltiplicano entrambi i membri per c² e si sviluppa, si perviene all'equazione:

Einstein ebbe il genio di intendere che m_d c² é l'ENERGIA TOTALE del corpo. Essa risulta la somma dell'energia cinetica  , fornita dal moto, e dell'addendo m₀ c² .

Einstein notò che, se v = 0, l'energia totale del corpo si riduce a m₀ c² ; egli chiamò quest'espressione ENERGIA A RIPOSO del corpo. Esiste quindi una perfetta equivalenza tra materia ed energia, espressa dalla celeberrima « formula di Einstein »:

L'esattezza dimensionale della formula é immediata:

[ m c² ] = [ m l² t^–2 ] = [ l² m t^–2 ] = [ E ]

Einstein sostituì la conservazione della massa stabilita da Antoine Lavoisier con quella della massa dinamica:

m_d  = m'_d  + m''_d  + m'''_d  + m^IV_d  + ......

e, se si moltiplica per c :

  m_d  c = m'_d c + m''_d c + m'''_d c + m^IV_d c + ...

ovvero:

m_d^tot  c² = m'₀ c² + 1/2 m'₀ v² + m''₀ c² + 1/2 m''₀ v² + ...

Questo prende il nome di conservazione della massa-energia: in ogni fenomeno si conserva sempre la somma delle masse e delle energie coinvolte.

Il risultato ottenuto è importantissimo, poiché significa che massa ed energia possono trasformarsi indifferentemente l'una nell'altra; in termini euristici, non è sbagliato dire che in un processo interviene « un chilo di energia »! Questo giustifica tra l'altro l'abitudine, assai diffusa nella Fisica della Materia, di misurare le masse delle particelle con unità energetiche. Facciamo un esempio semplice: la massa dell'elettrone, com'è noto, è di 9 * 10^-31 Kg. Ma il chilogrammo è un'unità troppo grande per le particelle su scala nucleare! Determiniamo allora l'energia a riposo in Joule di un elettrone attraverso la (4.2):

Anche il Joule è un'unità troppo grande su questa scala, un po' come se noi pretendessimo di misurare le nostre altezze in anni luce. Allora utilizziamo l'elettron-Volt, definito come l'energia posseduta da un elettrone che si muove nella differenza di potenziale di un Volt. Poiché la carica di un elettrone vale notoriamente  , si ha:

perché un Volt è pari ad un Joule su un Coulomb. L'energia a riposo di un elettrone vale perciò:

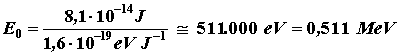
Dove MeV indica il Megaelettron-Volt, cioè un milione di elettron-Volt.

Purtroppo però l'equazione (4.2), oltre ad essere una delle pietre miliari della Fisica del Novecento, ha anche un tragico rovescio: costituisce infatti il fondamento teorico delle armi nucleari, in grado di trasformare una piccola massa in un enorme quantitativo di energia, che si libera con effetti catastrofici. Prima di proseguire in questa affascinante unità soffermiamoci un attimo a riflettere su questo punto. Lo stesso Einstein comprese la sciagurata possibilità di utilizzare a fini bellici la sua più importante scoperta allorché nel 1938, proprio mentre si profilava la Seconda Guerra Mondiale con l'invasione della Cecoslovacchia da parte di quell'Hitler che già lo aveva costretto all'esilio negli USA a causa dei suoi deliranti proclami contro la stirpe ebraica, il fisico Otto Hahn (1879-1968) ed il chimico Fritz Strassman (1902-1980) da Berlino annunciavano al mondo la scoperta della fissione nucleare. Allora, temendo che se Hitler fosse riuscito a costruire per primo la bomba atomica la avrebbe usata per ridurre il mondo ai suoi piedi, il 2 agosto1939 Einstein indirizzò al Presidente degli Stati Uniti Franklin Delano Roosevelt una lettera, nella quale chiedeva l’inizio del programma nucleare. Il risultato di quel programma è, purtroppo, ben noto: centinaia di migliaia di morti nelle città martiri di Hiroshima e Nagasaki. Einstein non si perdonò mai di aver scritto quella lettera, e si impegnò fino all'ultimo dei suoi giorni in campagne pacifiste.

Altre conseguenze inimmaginabili della (4.1) saranno esaminate nel paragrafo 4.3.