

Fino a meno di un secolo fa, quasi tutti i cosmologi credevano in un universo eterno, che sarebbe durato per sempre senza cambiamenti significativi. Tuttavia, la scoperta ad opera di Edwin Hubble e Georges Lemaître che l'universo è in espansione, e che quindi ha avuto un inizio, ha reso pressante stabilire se esso avrà o meno una fine. A questo punto, le ipotesi sul destino remoto del cosmo si possono ridurre a due sole alternative. L'espansione continuerà in eterno? Oppure, per effetto proprio dell'attrazione gravitazionale fra le galassie e gli ammassi di galassie, essa è destinata a far giungere l'universo a una dimensione massima, dopo la quale ricomincerà a decrescere? Pensiamoci bene: ciò significa chiedersi se l'universo può tornare a chiudersi su sé medesimo, andando a concentrarsi in quella stessa singolarità dalla quale è nato.
Le due alternative prendono il nome rispettivamente di "universo aperto" e di "universo chiuso" (tra poco vedremo che ve ne è una terza, quella dell'"universo piatto"). Esse dipendono chiaramente dal confronto tra la velocità dell'espansione e la densità della materia dispersa nello spazio, dalla quale dipende l'interazione gravitazionale che può "richiudere" l'universo. Quale che fosse l'intensità iniziale dell'espansione, la gravitazione é una forza estremamente debole, come ammetteva già Mago Merlino, e può essere in grado di rallentare l'espansione fino al punto di arrestarla solo se nell'Universo c'é una quantità sufficiente di materia. Viene chiamata densità critica dell'universo il valore minimo necessario affinché l'attrazione gravitazionale arresti l'espansione e riporti il cosmo al punto di partenza.
Come calcolare tale densità critica? Consideriamo un ammasso di galassie, che per semplicità avrà simmetria sferica. Indicando con ρ la densità della materia, la massa totale M del sistema sarà espressa dalla semplice formula:
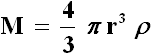
Fissiamo ora la nostra attenzione su una galassia di massa m, localizzata sulla superficie della suddetta sfera. L'energia potenziale da essa posseduta nel campo gravitazionale dell'ammasso sarà pari a:
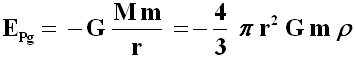
Ora, per la Legge di Hubble-Lemaître, la galassia considerata si allontana con velocità v = H r, per cui la sua energia cinetica sarà pari a:
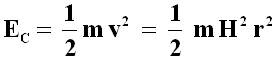
Di conseguenza, l'energia meccanica totale posseduta dalla galassia che si sta allontanando è data dalla somma delle due ultime espressioni:
Quest'energia, come sappiamo, resta costante durante il moto. Ora:
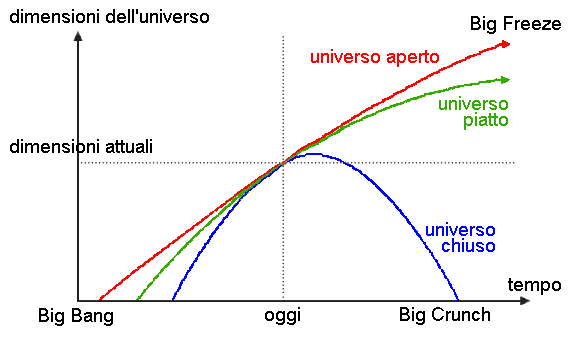
a) se Etot > 0, l'energia cinetica prevale sull'energia potenziale gravitazionale, e la galassia considerata (così come tutte le altre dell'ammasso) si allontana sempre più dalle altre senza mai tornare indietro. L'universo è aperto.
b) se Etot < 0, l'energia potenziale gravitazionale prevale sull'energia cinetica, e quindi, per effetto della gravità, la galassia considerata non potrà mai abbandonare l'ammasso. L'universo è chiuso.
c) se Etot = 0, la distribuzione della materia è tale che le galassie dell'ammasso si trovano in una sorta di equilibrio tra espansione ed attrazione gravitazionale. Si tratta di una situazione limite in cui l'espansione tende a zero solo dopo un tempo virtualmente infinito, la velocità diminuisce fino ad andare asintoticamente a zero, e si parla di universo piatto.
Osserviamo che la (1) può essere riscritta così, mettendo in evidenza alcuni termini:
Generalizziamo il discorso all'intero universo, in modo che ρ rappresenti la densità universale, e fissiamo la nostra attenzione sul rapporto 3 H2 / 8 π G. Esso ha le dimensioni di una densità:
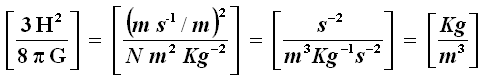
Essa è proprio la densità critica ρC che stiamo cercando, e che quindi ha l'espressione:
Infatti, in tal modo la (2) diventa:
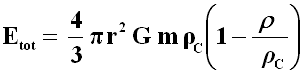
Di solito, anziché della densità critica ρC, ci si serve nei calcoli di un parametro adimensionale, il parametro di densità Ω, definito come il rapporto tra la densità effettiva dell'universo e la densità critica:
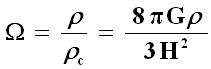
per cui la (2) in definitiva diventa:
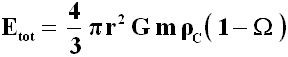
a) Se Ω < 1, Etot > 0 e l'universo è aperto;
b) se Ω > 1, Etot > 0 e l'universo è chiuso;
c) se Ω è esattamente pari a 1, Etot = 0 e l'universo è piatto.
Dunque la (3) ci fornisce proprio la densità critica da noi cercata! Essa può essere definita come il valore della densità dell'universo in corrispondenza del quale la velocità di fuga delle galassie risulta pari alla velocità dedotta dalla costante di Hubble-Lemaître.
Sostituiamo i valori oggi accettati per queste costanti. In una lezione precedente si è detto che H = (71,0 ± 2,5) km/s per Megaparsec, e siccome un Megaparsec misura circa 106 x 3,26 x 9,464 x 1012 Km = 30,85 x 1021 m, si ha:
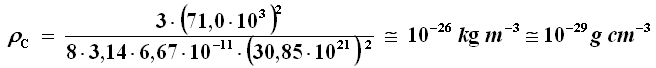
Questo valore corrisponde a una densità di non più di cinque atomi di idrogeno per ogni metro cubo di spazio. Ma quanto vale di preciso Ω, e quindi ρ?
A questa domanda gli scienziati cercano di rispondere da mezzo secolo a questa parte; purtroppo, però, la risposta é quanto mai incerta. Se la materia esistente nell'universo fosse sufficiente a raggiungere la densità critica, l'universo potrebbe richiudersi; in un tempo imprecisato l'espansione dovrebbe rallentare al punto da arrestarsi, per poi invertire il senso di marcia, cosicché le Galassie finirebbero per piovere l'una sull'altra, concentrandosi tutte verso un unico punto. Avverrebbe insomma quello che gli astrofisici chiamano il Big Crunch: l'aumento di densità farebbe aumentare il campo di radiazione, e quindi la temperatura; le galassie e le stelle si disgregherebbero, le forze tornerebbero a riaccoppiarsi mano a mano che l'energia cresce, e alla fine tutto tornerebbe al punto da cui tutto è cominciato: una singolarità in cui si concentrerebbe tutta la massa e tutta l'energia dell'Universo, a densità e temperatura inimmaginabili. Giunti a questo punto, non vediamo ragione perché l'universo non dovrebbe riesplodere nuovamente in un secondo Big Bang, pronto a ricostruire un nuovo universo, magari più bello di quello di prima. É la dottrina dell'eterno ritorno, che immagina il mondo come un continuo prodursi e disfarsi, in una sequenza infinita. Nella civiltà greco-romana, essa fu propugnata dai riti orfici, per i quali il tempo si ripeteva succube del fato, come se fosse la ruota in cui tutti gli esseri eternamente rinascono, muoiono e si ricompongono allo stato originale. L'eterno ritorno poi è un concetto cardine della filosofia indiana e della filosofia buddhista, dove viene chiamato Samsāra e rappresentato con una ruota, che solo il nirvana può spezzare. Secondo le dottrine indù ci troveremmo nel periodo detto Kali-Yuga, la quarta fase di un ciclo più lungo chiamato Mahâ-Yuga. I quattro periodi secondari detti Yuga sono Krita-Yuga, Tréta-Yuga, Dwâpara-Yuga e l'attuale Kali-Yuga; da notare la corrispondenza con le quattro età dell'antichità greco-romana: l'età dell'oro, dell'argento, del bronzo e del ferro. L'idea dell'eterno ritorno era presente anche nelle civiltà precolombiane d'America, fondata sulla ciclicità delle ere cosmiche. Con riferimento invece ai regimi politici, l'eterno ritorno venne descritto da Platone e da Polibio, e poi espresso da Giambattista Vico (1668-1744). L'eterno ritorno fu propugnato anche da varie correnti della Massoneria e dall'attuale New Age, che parla di ciclicità delle ere e in particolare del passaggio imminente dall'Età dei Pesci all'Età dell'Acquario, ritenuta una nuova età dell'oro.

Rappresentazione artistica tradizionale del Samsāra
La stima della massa universale fatta dai cosmologi lascia però poche speranze che l'universo possa "richiudersi": la densità stimata dell'universo osservabile oscilla sui 10–30 g/cm3, ed è quindi appena un decimo della densità critica necessaria a chiudere il nostro cosmo. Alcuni fisici hanno allora sostenuto che particelle considerate senza massa nel Modello Standard, come il neutrino, abbiano in realtà una piccola massa a riposo, compresa fra un centomillesimo ed un decimillesimo di quella dell'elettrone, la più leggera particella la cui massa é sinora stimabile con un certo grado di sicurezza. Massa piccolissima, é vero, ma i neutrini nel cosmo potrebbero essere tantissimi, dato che li produce una gran quantità di reazioni nucleari; e così, grazie ad essi, il Cosmo potrebbe essere chiuso. Le recenti misurazioni, come quelle dell'esperimento giapponese detto SuperKamiokande, fanno però pensare che la massa del neutrino non possa superare gli 0,05 eV/c2, contro i 511.000 eV/c2 dell'elettrone, corrispondenti ad appena 10–37 Kg; ed allora, per quanto numerosi siano i neutrini dell'universo, essi non saranno mai sufficienti a richiuderlo. Ma in soccorso di coloro che credono ancora nell'eterno ritorno e nella possibilità di un universo ciclico arrivò la speranza dell'esistenza di una notevole quantità di materia invisibile, che i nostri telescopi non riescono a captare, ma i cui effetti gravitazionali si fanno sentire anche sulla materia ordinaria. Stiamo parlando di un'altra delle grandi questioni irrisolte della cosmologia moderna: l'esistenza della materia oscura, della quale parleremo nella prossima lezione.