![]()
|
"Nel cratere dello Snæffels Yökull che l'ombra dello Scartaris tocca alle calende di luglio, discendi, o coraggioso viaggiatore, e giungerai al centro della Terra, cosa che io feci. Arne Saknussem" J.Verne, "Viaggio al Centro della Terra" |
.
A.1 Perchè i gravi non cadono esattamente verso il basso
Vogliamo chiudere questo ipertesto con alcuni approfondimenti che riguardano direttamente la gravità terrestre. Nel presente paragrafo amplieremo quanto visto nel § 3.2 circa le variazioni con la quota dell'accelerazione di gravità terrestre, mentre nel successivo dimostreremo come il campo gravitazionale di un corpo esteso sia equivalente a quello di una massa puntiforme concentrata nel suo baricentro. Nel terzo vedremo come varia il campo gravitazionale all'interno della Terra, ed infine nel quarto accenneremo al cosiddetto problema del "Pozzo di San Patrizio".
Nel suddetto paragrafo si è visto che l'accelerazione di gravità terreste cambia con la quota secondo la legge (3.4). Siccome l'espressione G MT / RT2 equivale all'accelerazione di gravità g0 a livello del mare, essa si può riscrivere anche così:
Occorre però una precisazione: la gravità terrestre non ha precisamente direzione radiale. Ciò è dovuto al fatto che la Terra ruota, e che quindi, oltre alla forza di gravità, agisce la forza centrifuga. Queste due si compongono, alterando la direzione della gravità locale come mostra la figura sottostante.

L'accelerazione di gravità al livello del mare è pari a g0, mentre l'accelerazione centrifuga è diretta in direzione radiale, ovvero perpendicolare all'asse di rotazione terrestre, ed il suo modulo vale:
![]()
Scomponiamo quest'ultima nelle due direzioni orizzontale (rispetto alla superficie terrestre) e radiale. Detta λ la latitudine, si avrà:
Ma, se R è il raggio terrestre:
![]()
e quindi le (A.2) diventano:
In direzione radiale, l'accelerazione centrifuga si compone con la gravità terrestre, dando luogo alla componente:
![]()
mentre g0 ha componente nulla in direzione orizzontale. Si ha così:
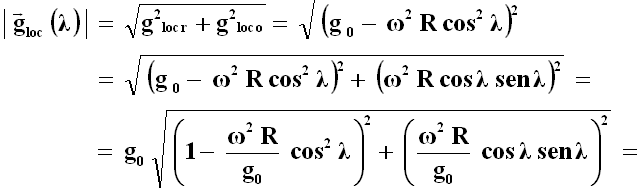
Chiamiamo ora:

Dato che ω2 R è un'accelerazione, se ne deduce che ξ è un parametro adimensionale. L'espressione di gloc si trasforma perciò nel modo che segue:

Osserviamo che ω = 2 π / T = 7,27 x 10–7 s–1, dunque:
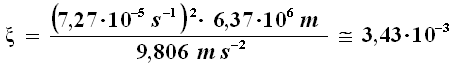
Essendo ξ così piccolo, mi sento autorizzato a trascurarne il quadrato, ottenendo:
Osserviamo ora che, se ξ << 1:
![]()
e perciò la (A.4) fornisce in definitiva:
Rappresentando questa funzione su un grafico cartesiano, otteniamo:
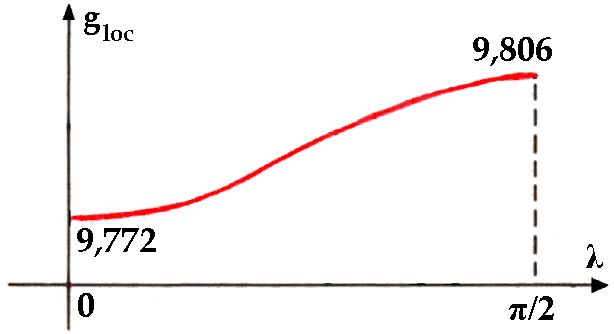
Se λ = 0 (all'equatore), di ha cos λ = 1 e gloc = g0 (1 – ξ ), per cui l'accelerazione di gravità è minima e vale all'incirca 9,772 m/s2.
Se invece λ = π / 2 (ai poli), si ha cos λ = 0 e la gravità locale coincide con g0. Si osservi che questo è l'unico punto in cui l'accelerazione centrifuga è nulla, e la direzione di gloc coincide effettivamente con la verticale.
A ciò si potrebbe aggiungere il fatto che la Terra non è una sfera perfetta, ma è schiacciata ai poli: la differenza tra raggio equatoriale e raggio polare incide su gloc per alcune parti su un milione.
Infine, si noti che, se all'equatore (λ = 0) avessimo ξ = 1, per la (A.5) la gravità sarebbe esattamente annullata dalla forza centrifuga, e all'equatore i corpi sarebbero praticamente privi di peso. Questo si verifica se:

Ma allora il periodo di rotazione terrestre (cioè la durata del giorno) dovrebbe essere:
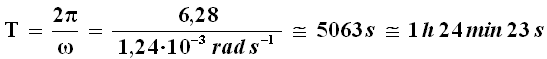
Si tratta circa di un diciassettesimo della durata attuale del nostro giorno. Se ne conclude che, se la velocità di rotazione terrestre fosse 17 volte maggiore, all'equatore la gravità sarebbe praticamente zero!
.
A.2 Se le masse non sono puntiformi
Vogliamo ora dimostrare uno dei punti cardini della teoria della Gravitazione Universale di Newton: l'effetto di una grande massa estesa è lo stesso di una equivalente massa puntiforme concentrata nel suo baricentro. Il calcolo non è banale, e proprio per condurlo in porto Isaac Newton inventò il calcolo integrale; chi non se la sente di affrontare tutto il ragionamento, salti subito alle conclusioni.

Consideriamo un guscio sferico di raggio a e spessore infinitesimo e dividiamolo in tante strisce sferiche, ottenute tagliandolo con piani perpendicolari al diametro AB; tutte hanno il centro su AB. Consideriamo un punto P esterno alla sfera sul prolungamento della retta AB, a distanza r dal centro C. Se 2θ è l'apertura della striscia sferica ( 0 < θ < π ), il raggio QH di ogni striscia misura a sen θ; l'angolo sotto cui il centro della sfera "vede" la striscia sferica sarà dθ, trattandosi di una misura infinitesima. Lo spessore della striscia sarà allora pari ad a dθ, dato che l'arco è pari al raggio per la misura dell'angolo in radianti. Moltiplicando lunghezza e altezza della striscia, posso trovarne l'area assimilandola ad un rettangolo:
![]()
Se M è la massa totale distribuita sulla superficie sferica, la sua densità sarà pari alla massa totale divisa per la superficie, cioè ad M / 4 π a2. Dunque la massa distribuita sulla striscia sferica vale:
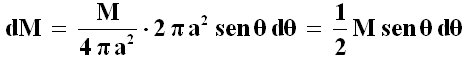
Tutti i punti della striscia si trovano alla stessa distanza R (θ) da P, dunque per la (4.1) il punto P avverte un'energia potenziale pari a:
essendo m la massa posta nel punto P. Dobbiamo dunque esprimere . Usiamo il teorema di Carnot applicato al triangolo CPQ:
![]()
a ed r sono costanti. Differenziando ambi i membri di quest'ultima si trova:
![]()
da cui:
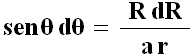
La sostituisco nella (A.6) ed ottengo:
Per ottenere l'energia gravitazionale in P dovuta a tutto il guscio sferico, devo integrare su R. L'angolo θ varia tra 0 e π, H si muove tra A e B, quindi R varia tra AP = r – a e BP = r + a. Si ha così:
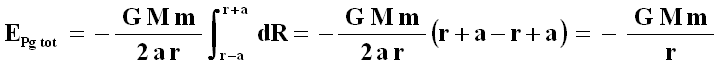
Se ne deduce che un guscio sferico di spessore infinitesimo e massa M genera nello spazio circostante lo stesso campo gravitazionale che eserciterebbe un corpo puntiforme di massa M posto nel suo centro. Un risultato fondamentale, che però nessuno può dare per scontato, ed infatti, come abbiamo visto, Newton vi arrivò solo dopo una dimostrazione lunga e complicata.
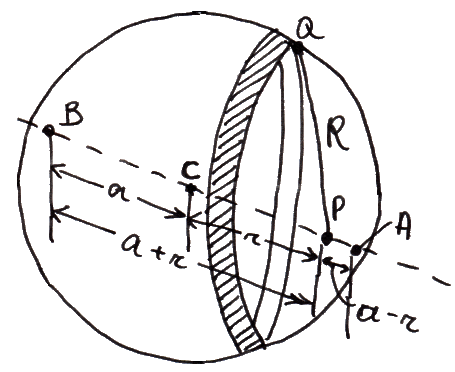
Questo vale se il punto P è esterno al guscio. E se è interno? Il discorso ora fatto resta valido, però cambiano gli estremi di integrazione della (A.7). Stavolta, infatti, R varia da AP = a – r a BP = a + r. Sembra una differenza banale, ma non lo è affatto, giacché si ottiene:
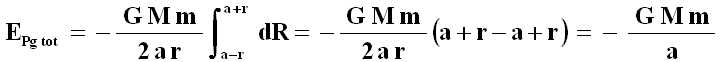
Ma a è costante. Ne consegue che un punto interno a un guscio sferico omogeneo avverte un'energia potenziale costante, indipendentemente dalla sua posizione! Fuori dal guscio, l'energia potenziale va come 1 / r ; dentro, è costante:

Chi conosce i fondamenti dell'analisi matematica sa che la forza è data dalla derivata dell'energia potenziale rispetto ad r, e quindi si ha:

Come si vede nei grafici sottostanti, l'energia potenziale è continua dentro e fuori il guscio sferico, ma la forza no! Questo vuol dire che un corpo, inizialmente all'interno di un guscio sferico, che lo attraversa e ne esce, sente improvvisamente la forza G M m / r2!

All'interno del guscio sferico omogeneo il campo gravitazionale è invece nullo, come all'infinito. Perchè? Si osservi la figura qui sotto. Un punto P interno al guscio sferico subisce l'attrazione verso sinistra della calotta di area S e verso destra della calotta di area S'. La massa distribuita sulla calotta è direttamente proporzionale alla sua area, che a sua volta è direttamente proporzionale alla sua altezza, perchè S = 2 π a h.
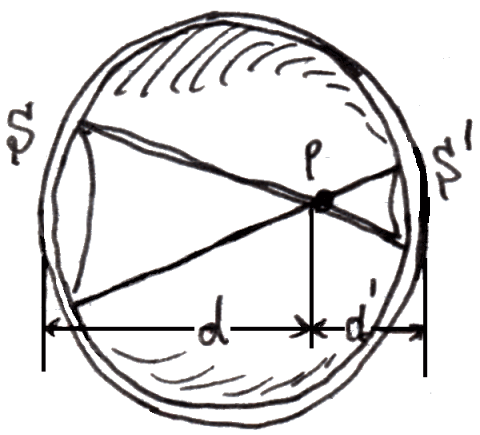
Detti r ed r ' i raggi delle calotte, come si vede nella figura qui sotto, si ha:
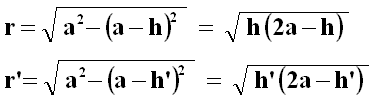
Se ho cura di scegliere coni di piccola apertura, trovo h , h' << 2 a, perciò:
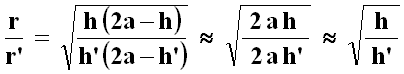

Ma, come si vede qui sopra, i coni proiettati da P verso le due calotte sono simili tra loro, e quindi i raggi di base sono direttamente proporzionali alle rispettive altezze d e d':
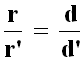
Il confronto tra le ultime due espressioni mi dice che:
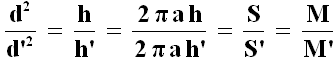
da cui si ricava facilmente:

Quindi il punto P è soggetto a forze uguali e contrarie! Ripetendo il ragionamento per tutte le calotte opposte viste da P, se ne conclude che effettivamente P non è soggetto ad alcuna azione gravitazionale!
La sfera tuttavia è tridimensionale: dunque, per conoscere l'azione gravitazionale da essa prodotta devo integrare due volte. La prima integrazione è stata eseguita, passando dalla striscia al guscio sferico; ora dobbiamo passare dal guscio alla sfera piena. All'uopo, immaginiamo la nostra sfera come una cipolla, costituita da tantissimi gusci sovrapposti, ciascuno di spessore infinitesimo. Supponiamo che il punto P considerato sia esterno alla sfera; possiamo allora immaginare che le masse Mi di tutti gli N gusci siano concentrate nel loro centro, tenendo fissa la distanza fra il centro e il punto P; ciò che cambia è solo la massa dei gusci. Ne consegue che l'energia potenziale gravitazionale è pari alla somma delle energie potenziali gravitazionali di tutti i gusci:
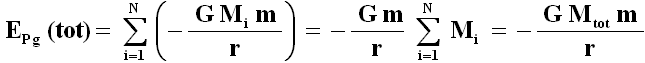
Ne consegue che l'azione gravitazionale esternamente ad una sfera è la stessa che si avrebbe se la sua massa fosse tutta concentrata nel suo centro. Questo risultato non richiede necessariamente l'omogeneità della densità; richiede però che essa sia distribuita almeno con simmetria sferica, che cioè sia indipendente dall'angolo θ. Infatti, ciò significa che la densità può variare lungo il raggio, ma che ogni guscio sferico mantenga la propria densità costante in ogni punto. Se invece nella sfera vi sono delle zone a densità maggiori delle altre, il risultato non è più riproducibile, e si ottiene che il campo gravitazionale dipende anche da θ. Si hanno cioè delle anomalie gravitazionali.

Analisi
gravimetrica del cratere Einstein A sulla Luna,
all'interno del cratere Einstein (credits LOLA/NASA)
Questo suggerisce un metodo geniale da usare per le prospezioni geologiche: misurando l'accelerazione di gravità sulla superficie della Terra e studiandone le anomalie locali, è possibile determinare se in profondità vi sono o meno delle miniere, delle concentrazioni di minerali con densità maggiore della roccia circostante, o delle falde di acqua, petrolio o gas naturale con densità minore della roccia che le circonda. È il cosiddetto metodo gravimetrico. Questo metodo ha permesso di individuare i codiddetti mascon (dall'inglese "mass concentration"), zone poste sotto la superficie della Luna o di altri pianeti con anomalia gravitazionale positiva, cioè con notevole concentrazione di massa ad alta densità. Sulla Luna si trovano ad esempio notevoli mascon sotto i grandi mari (Mare Crisium, Mare Humorum, Mare Imbrium, Mare Nectaris, Mare Serenitatis, Mare Smythii...), il che ci ha permesso di determinare che si tratta in effetti di colossali bacini da impatto. Giganteschi meteoriti si schiantarono contro il nostro satellite naturale quando il Sistema Solare era giovane, penetrando sotto la superficie lunare e provocando la parziale fusione del mantello e la riemersione di colate laviche in abbondanza; solidificatesi, esse diedero vita alle piatte distese rocciose che noi chiamiamo mari. Se invece il meteorite era più piccolo, l'accumulo di roccia fusa attorno al punto dell'impatto dava vita ad un cratere (in latino "vaso a bocca larga"), mentre il "risucchio" provocava l'innalzarsi di un picco centrale, ancor oggi visibile all'interno di molti crateri lunari.

Sempre l'analisi gravimetrica ha permesso di appurare che la Terra non è esattamente sferica: oceani, catene montuose e disomogeneità di densità generano un campo gravitazionale che differisce, seppure di poco, da quello di una massa puntiforme. Nel 2009 l’ESA ha inviato in orbita il satellite GOCE (Gravity field and steady-state Ocean Circulation Explorer) proprio per misurare queste disomogeneità con grande accuratezza, fino a 10–5 m/s2, e quindi per determinare la forma della Terra con una precisione mai raggiunta prima. Nell’immagine qui sopra (presa da questo sito) si vede un modello del campo gravitazionale della Terra, e quindi l'aspetto che la Terra assumerebbe se su di essa la gravità fosse la stessa in tutti i punti. In questo modello, il nostro mondo appare di forma ovale e pieno di bitorzoli come una patata! Sono innumerevoli i campi in cui i dati di GOCE potranno essere utilizzati, dallo studio della circolazione oceanica e di tutta la climatologia che ne consegue, all’analisi della densità dell’aria e dei venti, alle applicazioni alla geodesia.
Per chi è interessato, un'altra applicazione del calcolo integrale alla determinazione del campo gravitazionale di masse non puntiformi sarà discussa nella soluzione dell'esercizio 5, alla fine di questo ipertesto.
Edizione del 1900 di "Viaggio al Centro della Terra"
.
A.3 Viaggio al centro della Terra
Resta ora da determinare il campo gravitazionale all'interno di una sfera piena. Sarà avventuroso inoltrarci sotto la superficie terrestre, così come fecero il professor Otto Lidenbrock, suo nipote Axel e la guida islandese Hans nel celeberrimo romanzo di Jules Verne "Viaggio al Centro della Terra" (1864). Allo scopo, suddividiamo la sfera in due parti: una sfera concentrica di raggio r, con r < a, e la zona sferica compresa fra i raggi r ed a. Per quanto detto sopra, questa corona sferica non porta alcun contributo al campo gravitazionale, essendo tutta formata da gusci sferici che contengono il punto P. È come se quella materia non ci fosse, ai fini del calcolo dell'energia potenziale gravitazionale in P. Per la sfera interna applichiamo il risultato trovato nel § precedente:
dove Mr è la massa della sfera di raggio r.

Se supponiamo che la densità della sfera sia costante con la profondità, allora le masse sono direttamente proporzionali ai volumi:
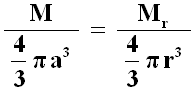
Da qui si ricava:
E sostituendo nella (A.8):
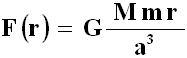 (A.10)
(A.10)
Dunque, all'interno delle masse il campo gravitazionale è direttamente proporzionale alla distanza dal centro. All'esterno di esse, invece, la forza decresce come l'inverso del quadrato della distanza. Se r = a, la (A.10) dà esattamente il valore che ci attendiamo alla superficie del pianeta, e quindi la funzione F(r) è continua:
Osserviamo che il campo cresce fino ad r = a, poi decresce fino ad appiattirsi a zero all'infinito. Questo ha una spiegazione fisica ben precisa: la diminuzione dovuta all'inverso del quadrato lungo il raggio della sfera è sovrastata dall'aumento della massa, proporzionale al cubo della distanza. Se perciò noi potessimo scendere davvero verso il centro della Terra, il nostro peso andrebbe scemando linearmente fino a zero. Se un uomo a 6370 Km di distanza dal centro della Terra pesa 70 Kg, per la (A.10) a 2000 Km di profondità peserebbe:
![]()
e nel centro della Terra si troverebbe a pesare esattamente zero. Il grafico soprastante in pratica rappresenta il peso di un corpo che, partendo dal centro della Terra, sale progressivamente verso l'alto fino all'infinito. Il peso di un corpo dunque è nullo solo al centro della Terra e all'infinito; ciò si esprime dicendo che la forza di gravità ha raggio d'azione infinito. Oggi sappiamo che la forza di gravità e la forza elettromagnetica hanno entrambe raggio d'azione infinito perchè le particelle che le mediano, rispettivamente il gravitone e il fotone (§ 8.3), hanno massa a riposo nulla, mentre le forze nucleari hanno corto raggio perchè le particelle che le mediano sono dotate di massa.
Il risultato or ora trovato ci permette di completare il discorso iniziato nel § 3.2 e nel § A.1, estendendo la (A.1) al caso in cui scendiamo in un pozzo, anziché salire su di una torre. Se scendiamo ad una profondità p, allora r = R – p. Per la (A.10) si ha:
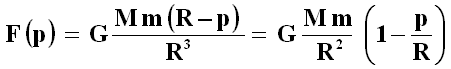
Dividendo entrambi i membri per m, e ricordando che G M / r2 è l'accelerazione di gravità g0 al livello del mare, troviamo una legge di variazione un po' differente dalla (A.1):
Sostituendo i valori numerici relativi al pianeta Terra, otteniamo:
![]()
Anche in questo caso la gravità diminuisce: sul fondo della Fossa delle Marianne, 10.994 metri sotto il livello del mare, si trova g = 9,789 m/s2. Però la diminuzione è più lenta di un fattore due dell'aumento avvertito dai corpi in salita al di sopra della superficie terrestre. Se scendo di un metro, la diminuzione risulta la metà di quella conseguente alla salita di un metro, e ciò è testimoniato dalla diversa pendenza delle due curve costruite per r < a e per r > a nel diagramma sopra ottenuto.
Osserviamo che i tre citati protagonisti del romanzo di Verne avrebbero dovuto osservare una sensibile diminuzione del loro peso, man mano che si inoltravano in profondità verso il centro della Terra; questo fatto era ben noto ai tempi dello scrittore francese, ma egli sceglie volutamente di ignorarlo per semplicità di narrazione, esattamente come nei film è telefilm di fantascienza, quando si vede esplodere un'astronave, si ode anche un forte rumore, sebbene nello spazio vuoto i suoni non si possano trasmettere. Si tratta di una evidente sospensione del senso comune per mere ragioni di spettacolo.

Naturalmente nessuno potrà mai scendere davvero di molte centinaia o addirittura migliaia di chilometri all'interno del Pianeta Terra, come immaginato da Jules Verne, o come nel film catastrofico "The Core" del 2003 di Jon Amiel, di cui qui sopra si vede la locandina con il celebre slogan "The only way out is in" ("L'unico modo per uscirne fuori è dentro."). Resterà per sempre intatto però il sogno di poter ritrovare davvero una pergamena del XVI secolo in scrittura runica cifrata che riveli il segreto per penetrare nel cuore ("the core") del pianeta Terra, come capitò al professor Lidenbrock:
«
In Sneffels Yoculis craterem kem delibat umbra Scartaris Julii intra calendas descende, audas viator, et terrestre centrum attinges. kod feci. Arne Saknussem
»
[Nel cratere dello Snæffels Yökull che l'ombra dello Scartaris tocca alle calende di luglio, discendi, o coraggioso viaggiatore, e giungerai al centro della Terra, cosa che io feci. Arne Saknussem]
.
A.4 Il Pozzo di San Patrizio
In quest'ultimo paragrafo vogliamo discutere un interessante problema che non è certo meno irrealistico, dal punto di vista tecnologico, della scampagnata fin dentro il nucleo terrestre. Immaginiamo di poter scavare una galleria che, da un punto qualsiasi della superficie terrestre, seguendo un diametro giunga fino al suo antipodo, passando per il centro del pianeta. Una simile ipotetica galleria prende il nome di Pozzo di San Patrizio, per via di un'antica leggenda irlandese, secondo cui Cristo in persona avrebbe indicato a San Patrizio (385–461), primo evangelizzatore dell'Irlanda, una caverna posta su un isolotto del Lough Derg, dove egli era solito ritirarsi in preghiera nell'isola; essa avrebbe comunicato direttamente con l'Inferno, e Patrizio la avrebbe utilizzata per mostrare le pene dell'Inferno agli increduli.
Lasciamo dunque cadere un corpo dentro questo vero e proprio pozzo senza fondo: che tipo di moto lo caratterizzerà? Nonostante le apparenze, il problema è abbastanza semplice. L'equazione del moto è rappresentata dal Secondo Principio della Dinamica:
![]()
La forza applicata alla massa m è quella gravitazionale:

Il segno meno è giustificato dal fatto che la forza ha sempre segno opposto all'accelerazione. Infatti l'accelerazione è positiva verso l'alto, cioè verso destra, mentre la forza è diretta verso il centro della Terra, cioè verso sinistra; una volta superato il punto « al qual si traggon d'ogne parte i pesi » (Inf. XXXIV, 111), come lo definì Dante, la forza tira verso destra, mentre l'accelerazione è diretta a sinistra.
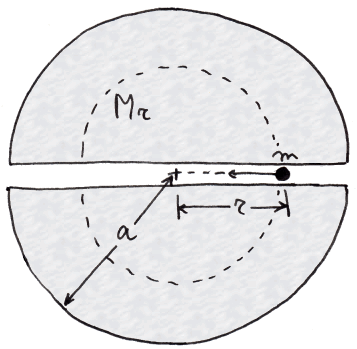
Trovandosi la massa m all'interno della Terra, per quanto detto nel § A.2, il guscio sferico con r > a risulterà ininfluente, ed essa avvertirà solo l'azione della sfera di raggio r, che ha una massa Mr data dalla (A.9). Si ha così:
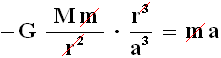
che si può riscrivere:
La Meccanica ci insegna che l'unico moto nel quale l'accelerazione è direttamente proporzionale allo spostamento ed ha verso opposto ad esso è il moto armonico. Una dimostrazione molto semplice di questa affermazione, per chi conosca i fondamenti del calcolo infinitesimale, è la seguente. L'accelerazione è la derivata della velocità rispetto al tempo, e quindi è la derivata seconda dello spostamento rispetto al tempo. La (A.12) dà dunque luogo alla seguente equazione differenziale del secondo ordine:
Essa ha una soluzione generale del tipo:
![]()
Infatti, essendo del secondo ordine ho bisogno di due costanti da determinare. Derivandola due volte si ottiene:
E sostituendo nella (A.13), dopo opportune semplificazioni:

Da cui si ricava:

Questa è la pulsazione del moto armonico prodotto dall'attrazione gravitazionale.

Il
cosiddetto "Pozzo di San Patrizio" ad Orvieto, costruito tra il 1527
e il 1537 da Antonio da Sangallo per volere di Papa Clemente VII
.
Determiniamo ora le costanti A e B partendo dalle condizioni iniziali. Supponendo che il corpo parta da fermo e con velocità nulla, dovrà risultare:
![]()
Sostituendo nelle (A.14) si ottiene subito A = 0, B = a. Ne consegue che l'equazione del moto è:
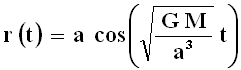
Osserviamo che G M / a2 = g, cioè è pari all'accelerazione di gravità al livello del mare, per cui la precedente si può anche riscrivere:
Questa è l'equazione del moto cercata. Sostituendo i dati del pianeta Terra si ottiene:
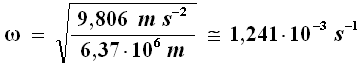
Il periodo di questo moto armonico è allora dato da:

Si osservi che la velocità (cioè r') è nulla quando la massa raggiunge la superficie terrestre, ad un'estremità o all'altra del tunnel. Incredibilmente, lasciando cadere la massa nel nostro Pozzo di San Patrizio, lo vedremo riemergere dopo circa un'ora e mezza all'altra estremità, arrestarsi per un attimo, quindi ricominciare a cadere, e così via! La velocità è massima quando r = 0, cioè al centro della Terra. Detto t1 il tempo necessario per arrivarci, per la (A.15) sarà:
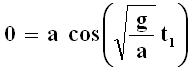
da cui:

Ora, la velocità del mio corpo vale:

e quindi:
![]()
L'accelerazione della nostra massa vale invece:
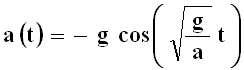
Quindi al centro della Terra l'accelerazione della massa vale esattamente g; è cioè pari all'accelerazione di gravità alla superficie del pianeta! Tuttavia vi disilludo subito dalla speranza di aver scoperto il moto perpetuo: infatti anche in questo caso l'inevitabile attrito ben presto rallenta il corpo, le oscillazioni diventano smorzate e il corpo finirà per arrestarsi definitivamente al centro della Terra.

Analogamente si potrebbe dimostrare che è armonico anche il moto di una massa lungo un tunnel scavato attraverso una corda della sfera terrestre, come si vede nella figura soprastante; lascio però al volenteroso lettore il compito di eseguire questa dimostrazione, sulla base dei calcoli che abbiamo svolto fino a qui.
.
E con questo, è davvero tutto. Per passare a cimentarvi con gli esercizi conclusivi, che vi diranno se avete compreso o meno i problemi dibattuti in questo ipertesto, cliccate qui. Buona soluzione! Per tornare all'indice, invece, il link è questo.
![]()