Azioni a distanza

"Cerco un centro di gravità permanente
che non mi faccia mai cambiare idea
sulle cose, sulla gente..."

F. Battiato, "La voce del padrone", 1981

Il lettore attento si sarà reso conto che tutto ciò di cui abbiamo parlato nel capitolo precedente presuppone un postulato fondamentale, non facilmente "digeribile": le masse possono influenzarsi a distanza, senza toccarsi tra di loro.

In effetti, se giochiamo a biliardo, è ovvio che una palla non si muove sul tavolo verde finché un'altra palla non la urta, cioè finché non vi è un contatto materiale fra di essi. Io stesso non posso spostare quella pallina sul tavolo da biliardo se non la tocco con la mano. La Dinamica conosce azioni a contatto, ma non riesce a spiegare come mai la Luna orbita intorno alla Terra senza che esse si tocchino. Newton stesso si pose il problema, ma nei suoi celeberrimi "Principia Mathematica" liquidò la questione con una locuzione rimasta proverbiale: « Hypotheses non fingo », cioè "non avanzo ipotesi", poiché secondo lui il problema era di natura filosofica e non scientifica. Ma siamo davvero sicuri che tale dilemma sia del tutto estraneo alla Fisica? Essa non indaga forse le azioni reciproche tra i corpi? E non ha il dovere di studiarle anche se esse non appaiono immediatamente comprensibili? Non era forse incomprensibile anche il moto della Luna intorno alla Terra, prima che Newton lanciasse l'idea della forza di gravità? E non era incomprensibile il fatto che tutti i corpi cadessero verso la Terra, tanto che si doveva ricorrere a un ipotetico e quasi magico "moto naturale" per renderne conto?

Fu in seguito a questo ragionamento che, nel XIX secolo, e quindi centocinquant'anni dopo la morte di Newton, l'inglese Michael Faraday (1791-1867) propose di introdurre il concetto di campo. Secondo questa visione, ogni massa sarebbe in grado di "deformare" lo spazio circostante, facendo comparire un vettore forza applicato in ogni singolo punto dello spazio.

Come rilevare questo "campo" di forze gravitazionali? Se nel punto A io pongo una massa m', essa avvertirà una forza F di intensità pari a:

Naturalmente il campo esiste anche se in A non c'è alcuna massa, ma la forza F può essere rilevata solo se in A la massa viene effettivamente posta. Naturalmente la massa m' deve essere assai più piccola di m, altrimenti anch'essa genererebbe un campo, come tutte le masse, e disturberebbe quello generato da m. È il solito, vecchio problema della misura; lo strumento di misura non deve mai perturbare la misura che si va facendo. Per questo diremo che in A va posta una massa campione estremamente piccola. Ma non basta.

Infatti la forza F dipende dalla massa campione m' posta in A: dunque, non è una buona misura di quello che chiameremo "campo gravitazionale". Se raddoppio m', raddoppio anche F. Invece io ho bisogno di qualcosa che dipenda solo dalla massa m che genera il campo e dalla distanza di m da A. L'idea che venne a Faraday è quella di introdurre un nuovo vettore, detto intensità del campo gravitazionale, dato dal rapporto tra la forza F e la massa campione m':

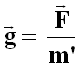
Come si vede, l'intensità di campo gravitazionale è definita come la forza esercitata per unità di massa; la sua direzione e il suo verso coincidono con quelli di F, per cui essa è sempre rivolta verso la massa che genera il campo. La sua espressione analitica è:

Introdurre il campo gravitazionale è insomma un "trucco" per eliminare la dipendenza della forza dalla massa campione. Ad ogni punto dello spazio posso perciò assegnare un vettore g di intensità data dalla (3.1), e diretto radialmente verso la massa che genera il campo. Ne consegue che tutti i punti di una superficie sferica di centro m e raggio r sono caratterizzati dall'avere lo stesso valore del vettore g, e quindi il campo generato da una singola massa è caratterizzato da una simmetria centrale o sferica, di questo tipo:

Se in un punto di tale superficie sferica pongo una massa m'', la forza avvertita si otterrà moltiplicando tale massa per il campo gravitazionale in quel punto:

Sono le dimensioni di un'accelerazione. Dunque il campo gravitazionale è un campo di accelerazioni, e non un campo di forze! Ogni massa "catturata" dal campo gravitazionale di m viene accelerata verso di essa. Se m è la massa MT della Terra, e la superficie sferica considerata è la superficie terrestre, il concetto di campo g va a coincidere con quello di accelerazione di gravità che, infatti, è indipendente dalla massa del corpo!

Grazie alla (3.1), che poi coincide con la (2.7) da noi analizzata nel capitolo precedente, è possibile ricavare le variazioni con la quota dell'accelerazione gravitazionale terrestre. Alzandosi di un'altezza h rispetto al livello del mare, infatti, basta ritoccare la formula come segue:

Se h è assai più piccolo del raggio terrestre, h² può essere trascurato (tecnicamente si dice che si tratta di un infinitesimo di ordine superiore), e il raggio terrestre al quadrato può essere raccolto come segue:

Se α è molto piccolo (α <<1), α² è un infinitesimo di ordine superiore e può essere trascurato. Si giunge così a questa utile formula approssimata:

Ora, nella (3.3) il rapporto 2h/R_T è per l'appunto assai piccolo, per piccoli dislivelli, per cui tale espressione in prima approssimazione può essere così semplificata:

Che la formula sia corretta ce lo dice quel segno meno: il termine fuori parentesi è l'accelerazione di gravità g al livello del mare, e man mano che si sale aumenta il termine da sottrarre a uno. Infatti l'accelerazione di gravità diminuisce lentamente man mano che si sale di quota. L'Everest è alto 8848 metri sul livello del mare, mentre il raggio medio della Terra misura circa 6.372.797 metri, dal che si deduce che:

ed essendo 9,7801 m/s² l'accelerazione di gravità a livello del mare, se ne conclude che sulla cima dell'Everest essa assume il 97 % di tale valore, cioè circa 9,5082 m/s². A chi desidera approfondire questo discorso, suggerisco di consultare il paragrafo A.1 dell'Appendice.

Da tutto questo si ricava che, se un corpo non si allontana mai molto dalla superficie della Terra, non più di quanto occorre per salire in cima ad un edificio, le variazioni con la quota dell'accelerazione di gravità possono essere ritenute trascurabili: il termine 2h/R_T è a tutti gli effetti da considerarsi nullo, e quindi il campo gravitazionale g a tutti gli effetti è da considerarsi costante in modulo in ogni punto. Ma anche direzione e verso sono costanti: se considero un ambiente abbastanza piccolo, come un'aula scolastica o un laboratorio, il centro della Terra è così lontano che i vettori di campo gravitazionale, anziché convergere tutti in un unico punto, si possono ritenere tutti paralleli e diretti verso il basso. Un campo costante in ogni punto in modulo, direzione e verso viene definito uniforme; il campo gravitazionale in un ambiente di piccole dimensioni è dunque da ritenersi uniforme. Naturalmente, su grandi distanze, comparabili con quella che ci separa dalla massa che genera la forza di gravità, ciò non è più vero, e i vettori convergono verso quest'ultima con una simmetria sferica; un campo di questo genere viene invece definito radiale.

Per questo non esiste un solo campo gravitazionale: ne esistono due! Viene definito:

a) campo gravitazionale in piccolo quello contenuto in uno spazio relativamente limitato, a grandi distanze dalla massa che genera il campo. Tale campo è uniforme e l'accelerazione di gravità g è costante in ogni punto in modulo, direzione e verso Tale è per esempio il campo di forze peso che noi percepiamo nella nostra vita quotidiana; la costanza della direzione di g verso il basso aveva spinto Aristotele a postulare l'esistenza del famoso "moto naturale" verso il basso.

b) campo gravitazionale in grande quello esteso ad uno spazio molto vasto, che comprende la massa stessa all'origine del campo. In questo caso il vettore intensità del campo gravitazionale è sempre diretto verso tale massa, e il suo modulo diminuisce allontanandosi da essa in ragione del quadrato della distanza, secondo la formula (3.1). Tale è il campo gravitazionale che circonda ad esempio il pianeta Terra, e viene avvertito dai satelliti artificiali e dalla Luna. Tale campo genera un moto curvilineo, descritto dalle Tre Leggi di Kepler.

Il campo gravitazionale può essere rappresentato con l'ausilio delle linee di campo (dette sovente anche linee di forza). Si definisce linea di campo una linea tangente, in ogni punto per il quale passa, al vettore campo in quel punto; la linea è orientata secondo il verso del vettore campo. Siccome, nel campo gravitazionale in grande, i vettori di campo sono tutti orientati verso la massa che lo genera, le linee di forza sono rappresentate da semirette concorrenti nella massa suddetta. Se però abbiamo più masse in gioco, le linee di forza non sono più semirette, ed assumono delle forme talora molto complesse. Nel caso invece del campo gravitazionale in piccolo, le linee di forza sono tutte rette verticali, parallele ed equidistanti tra di loro.

Da notare che il campo gravitazionale in grande si estende in linea teorica fino all'infinito, poiché il vettore intensità del campo tende a zero solo quando r tende all'infinito! Nella pratica, però, al di là di una certa distanza, gli effetti gravitazionali di una massa non sono più avvertibili.

Non so a voi, ma a me tutto questo fa venire in mente una celebre canzone di Franco Battiato del 1981: vi consiglio di ascoltarla a questo link.

Vogliamo ora mostrare come il campo gravitazionale, sia in grande sia in piccolo, sia conservativo, cioè come il lavoro compiuto sia indipendente dalla traiettoria, ma dipenda solo dal punto iniziale e dal punto finale. Cominciamo con il campo gravitazionale in piccolo. Si consideri il piano inclinato in figura: un corpo scivola senza attrito da A a B. Sia h l'altezza del piano inclinato, e sia l la sua lunghezza. Il percorso più breve da A a B è rappresentato dal percorso rettilineo lungo il piano inclinato; la forza che porta il corpo a scivolare è la forza peso P = m g. Se però il corpo segue l'inclinazione del piano, a spingerlo effettivamente non è l'intera forza P, ma solo la sua componente P_l, che definiremo "P longitudinale", essendo parallela al piano inclinato. Se α è l'inclinazione del piano, tale componente vale:

L'angolo che tale componente forma con lo spostamento è nullo, essendo i due vettori paralleli. E siccome il lavoro di una forza è pari al prodotto di essa per lo spostamento per il coseno dell'angolo compreso fra di essi, ne risulta che il lavoro vale:

Ora, dalla figura si ricava che l sen α = h, per cui il lavoro per andare da A a B lungo il tragitto più breve è pari a L = m g h.

Si consideri ora un percorso più lungo da A a B: prima faccio cadere il corpo da A a C, e poi lo trasporto senza attrito da C a B. Lungo CB, è facile rendersi conto che il lavoro è nullo. Infatti lo spostamento (senza attrito) da C a B è perpendicolare alla forza peso, e il coseno di 90° è pari a zero. Invece, quando il corpo si sposta da A a C, la forza peso è parallela allo spostamento (verticale), e dunque il lavoro è pari a:

La conclusione è che il lavoro compiuto per portare il corpo da A a B lungo il piano inclinato è lo stesso che si deve compiere per portarlo prima da A a C, e poi da C a B. Se fosse presente attrito, invece, il fatto che il percorso AB sia maggiore di quello CB comporterebbe che l'attrito sia minore nel secondo caso che nel primo, e dunque i due lavori sarebbero differenti, e dipenderebbero dal percorso seguito. Non è difficile dimostrare invece che, in assenza di attrito, qualunque percorso, anche curvilineo e molto complicato, che porti il corpo da A a B, richiederebbe di compiere un lavoro pari a L = m g h. Il campo gravitazionale in piccolo è dunque conservativo, come volevasi dimostrare.

Passiamo ora al campo gravitazionale in grande. Consideriamo la figura seguente, che illustra il campo gravitazionale generato dal pianeta Terra. Come si indovina dalla figura, io devo portare il mio corpo da A a B, e mi è richiesto il lavoro necessario. Il percorso più semplice in questo caso non è quello rettilineo da A a B, bensì quello che porta prima da A (chiamato anche A₀) a B₀ lungo un arco di circonferenza, e poi da B₀ a B in direzione radiale. In questo caso infatti il lavoro lungo A₀B₀ è nullo, come è avvenuto nel caso del piano inclinato da C a B, in quanto la forza di gravità newtoniana forma un angolo retto con lo spostamento. Il lavoro necessario per portare il corpo da A a B è dunque lo stesso che serve per portarlo da B a B₀, che determineremo in seguito. E lungo percorsi più complicati, come quello segnato in figura con il colore rosso?

Supponiamo di "approssimare" tale percorso con la spezzata costruita in figura intorno ad esso. Si procede in questo modo: si divide il segmento B₀B in cinque parti tra loro congruenti, e si tracciano cinque archi di circonferenza fino alla curva. Sia A₁ il primo di questi punti; con centro in O (il centro della Terra) si traccia un arco che tocca la curva in B₁, poi da questo si traccia una semiretta uscente da O e si segna su di esso un segmento B₁A₂ congruente ad AA₁; da A₂ si traccia un nuovo arco con centro in O fino a toccare la curva in B₂, e così via fino a raggiungere il punto B₅ (cioè il punto B). Si ottiene così una spezzata formata da cinque segmenti e cinque archi di circonferenza, che approssima la curva rossa AB:

Ora, lungo i quattro archi di circonferenza con centro in O (A₁B₁, A₂B₂, A₃B₃, A₄B₄ e A₅B₅) il lavoro della forza di gravità è nullo, poiché quest'ultima è sempre perpendicolare allo spostamento. I cinque segmenti (A₀A₁, B₁A₂, B₂A₃, B₃A₄ e B₄A₅) hanno come somma una lunghezza pari a B₀B₅, e quindi il lavoro lungo complessivo lungo questi cinque intervalli sarà pari a quello complessivo per andare da B₀ a B₅, che come abbiamo visto poco fa è pari a quello necessario per andare da A a B lungo un unico arco di circonferenza e un unico raggio. Naturalmente la spezzata suddetta approssima la curva AB molto grossolanamente; ma è possibile dividere B₀B₅ in dieci, cento, mille parti, e ogni volta la spezzata così ottenuta approssimerà in misura migliore la curva data. Al limite, sarà possibile dividere B₀B₅ in infinite parti, ed allora la spezzata coinciderà esattamente con la curva. Siccome questo ragionamento può essere ripetuto per qualunque curva che parte da A ed arriva in B, se ne deduce che il lavoro lungo ciascuna di esse è sempre lo stesso, e quindi anche il campo gravitazionale in grande risulta conservativo.

Vediamo ora di calcolare esplicitamente tale lavoro, poiché finora non lo abbiamo fatto. Per questo, ricorreremo anzitutto ad un metodo approssimato, per chi non abbia familiarità con l'Analisi Matematica. Abbiamo visto che il lavoro per andare da A a B lungo una qualsiasi traiettoria è pari a quello necessario per andare da B₀ a B lungo una semiretta uscente dal centro della Terra. Dividiamo allora tale spostamento B₀B in tanti spostamenti assai più piccoli B₀C₁, C₁C₂, C₂C₃... per mezzo dei punti C₁, C₂, C₃... le cui distanze dal centro della Terra O sono rispettivamente r₁, r₂, r₃... Invece r_A ed r_B saranno le distanze da O di B₀ (cioè di A) e di B. Noi calcoleremo il lavoro necessario per andare da A a B sommando i lavori L₁, L₂, L₃... compiuti dalla forza di gravitazione nei vari spostamenti infinitesimi.

Consideriamo dunque i punti B₀ e C₁, cioè i punti iniziale e finale del primo spostamento infinitesimo. In essi la forza di gravitazione per la (2.6) vale rispettivamente:

Ora, nel nostro caso il lavoro è pari al prodotto della forza per lo spostamento cambiato di segno, perchè l'angolo tra di essi misura 180°, essendo lo spostamento diretto verso l'esterno e la forza verso l'interno, e il coseno di 180° è pari a – 1. Ma, siccome la forza cambia man mano che mi sposto, quale forza moltiplico per lo spostamento? A questa domanda risponde il calcolo integrale. Per arrivare allo stesso risultato per via elementare, supponiamo che gli spostamenti B₀C₁, C₁C₂, C₂C₃... siano infinitesimi, cioè così piccoli che la forza lungo ciascuno di essi possa essere ritenuta costante (insomma, anziché vederla variare con continuità, la vedremo variare a scatti da B₀ a B). Approssimiamo inoltre la distanza di ogni segmento infinitesimo da O con la media geometrica delle distanze da O dei suoi estremi, cioè

. Allora la forza costante avvertita dai punti del segmentino B₀C₁ sarà pari a:

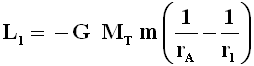
Ripetendo lo stesso procedimento per gli spostamenti infinitesimi successivi, si otterrà facilmente:

Sommando membro a membro tutti questi valori, e mettendo a fattor comune G M_T m, ci accorgiamo che tutti i termini del tipo 1/r si annullano, tranne il primo e l'ultimo! Ottengo perciò:

Questa è l'espressione del lavoro necessario per portare la massa m da A a B, qualunque siano i punti A e B dello spazio circostante la massa M_T. Come si vede, esso dipende solo da r_A e da r_B, non da tutti i punti intermedi, e questo a riprova del fatto che la forza gravitazionale in grande è conservativa, esattamente come quella gravitazionale in piccolo.

Naturalmente, si tratta di un calcolo approssimato. È però possibile dimostrare che anche un calcolo rigoroso porta allo stesso risultato espresso dalla (3.5). In tal caso, bisogna ricorrere al calcolo integrale; ciò che seguirà, quindi, potrà essere compreso solo da chi possiede già tale nozione. Se infatti chiamiamo dr la lunghezza infinitesima di ciascuno dei segmentini B₀C₁, C₁C₂, C₂C₃... considerati sopra, il lavoro infinitesimo compiuto in ciascuno di essi sarà pari a:

Il lavoro necessario per spostarsi da A a B si otterrà perciò integrando quest'espressione fra A e B:

Come si vede, si è ottenuto lo stesso risultato della (3.5)! Ora comprendiamo perchè Isaac Newton tardò tanto a pubblicare i propri studi sulla gravitazione universale: prima dovette mettere a punto il calcolo integrale, onde poter eseguire il calcolo rigoroso di tale lavoro!

È inoltre facile verificare che il lavoro compiuto dal campo gravitazionale in grande per spostare una massa m tra due punti A e B coincide con quello compiuto dal campo gravitazionale in piccolo, qualora la differenza di quota tra A e B sia molto più piccola del raggio terrestre. Siano infatti h_A e h_B le quote sul livello del mare dei due punti A e B. Dalla (2.7) infatti si ricava:

Se R è la distanza del livello del mare dal centro della Terra, potremo scrivere R_A = R + h_A e R_B = R + h_B. Sostituendoli nella precedente, si ottiene:

Se h_A ed h_B sono piccole rispetto ad R, potremo approssimare sia (R + h_A) che (R + h_B) con R, e allora R² a denominatore si semplificherà con R² a numeratore, e rimarrà solo L = m g (h_B – h_A), che è precisamente l'espressione del lavoro nel caso del campo gravitazionale in piccolo!

Vale la pena dedicare un paragrafo di questa nostra trattazione ad uno spinoso problema: perchè un satellite non può orbitare troppo vicino ad un pianeta? Per colpa delle cosiddette forze di marea: il pianeta attira a sé l'emisfero vicino del satellite più di quanto non faccia con l'emisfero lontano, e così finisce per frammentarlo. La distanza minima dal centro del pianeta alla quale il satellite può orbitare senza disgregarsi si chiama limite di Roche, in onore dell'astronomo francese Édouard Albert Roche (1820–1883), che lo determinò per primo nel 1848. All’interno del limite di Roche possono ruotare dei satelliti solidi solo se sono sufficientemente piccoli, poiché in tal caso le tensioni interne delle rocce non bastano per frammentarli.

Come determinare il limite di Roche? Vediamo di seguire il suo ragionamento. Anziché pensare a due metà emisferiche di un satellite sferico, modellizziamo il satellite sotto forma di due sfere di raggio R e massa m, tenute unite dalla forza di gravità. Dato che i loro due centri di massa distano 2R tra di loro, la forza di attrazione F_a può essere considerata pari a:

Supponiamo che il nostro satellite bisferico sia posto a una distanza r da un pianeta di massa M e di raggio R_P. La forza di attrazione F₁ tra il pianeta e la sfera più vicina sarà maggiore della forza F₂ tra il pianeta e la sfera più lontana. Le due forze sono date da:

Le due sfere percepiranno una forza di marea F_m che tenderà a separarle, e che sarà pari alla differenza tra le forze F₁ e F₂:

Le due masse si separeranno tra di loro se la forza F_m sarà maggiore della forza F_a che le tiene unite:

La (3.8) fornisce il valore del limite di Roche. Se il pianeta e il satellite hanno la medesima densità, il limite di Roche sta in un rapporto con il raggio del pianeta pari alla radice cubica di 16, cioè a 2,51984 volte il raggio del pianeta. Un satellite che disti dal suo pianeta meno di due raggi planetari e mezzo circa, è inesorabilmente distrutto dalle forze di marea.

Pianeta	Limite di Roche
Terra	16.000 Km
Marte	8.500 Km
Giove	175.000 km
Saturno	147.000 km
Urano	62.000 km
Nettuno	59.000 km

Phobos, il satellite più interno di Marte scoperto da Asaph Hall nel 1877, è prossimo al limite di Roche del suo pianeta, e siccome si trova sotto l'altitudine sincrona, esso è destinato entro 50 milioni di anni ad oltrepassare il limite e a disintegrarsi per effetto delle intense forze mareali.

È già accaduto, in passato, che dei satelliti si siano trovati all'interno del limite di Roche? La risposta è affermativa. Proprio Édouard Albert Roche, studiando gli anelli di Saturno, verificò che essi si trovano tutti all’interno del limite di Roche del pianeta, di poco superiore ai 2,44 raggi planetari per via delle differenze di densità tra il pianeta e gli anelli. Questo lo condusse a comprendere che, quando un pianeta nelle fasi appena successive alla sua formazione è avvolto da un disco di frammenti, la materia oltre il limite di Roche può aggregarsi formando uno o più satelliti, mentre all'interno di tale limite le forze di marea impediscono la formazione di satelliti sufficientemente grandi, e il materiale restante dà vita a sistemi di anelli. Come ulteriore conferma, le riprese delle sonde Voyager 1 e Voyager 2 dimostrarono che gli anelli non sono solidi, ma composti da cristalli di ghiaccio, in quanto trovandosi all'interno del limite di Roche non potevano che avere scarsa consistenza.

Le esplorazioni del Sistema Solare esterno mediante sonde automatiche (vedi § 5.5) hanno confermato che anche Giove, Urano e Nettuno sono circondati da sistemi di anelli, e per tutti e tre gli anelli si trovano internamente al limite di Roche per ciascun pianeta. Un tempo si pensava che gli anelli fossero formati dai resti di anelli disintegrati dalle forze mareali, oggi si pensa piuttosto che siano formati da materiale che non è riuscito a dar vita a delle lune a causa di tali forze. Esistono, negli anelli di Saturno e di Urano, dei minuscoli satelliti, ma sono troppo piccoli per essere distrutti dalle forze di marea. Essi sono chiamati "satelliti pastori" perchè, come il cane pastore tiene unito un gregge, così questi satelliti contribuiscono a mantenere gravitazionalmente stabili alcuni anelli. Così, Pan ruota nella Divisione di Encke all'interno dell'anello A, divisione generata dal medesimo satellite; Atlante tiene confinato l'anello A, mentre Prometeo e Pandora delimitano l'anello F, l'uno lungo il bordo interno e l'altra lungo il bordo esterno. Allo stesso modo, Cordelia e Ofelia sono i satelliti pastori interno ed esterno dell'anello Epsilon di Urano.

Prometeo, qui ripreso dalla sonda Cassini, tiene confinato l'anello F di Saturno

Del resto, che gli anelli intorno ai corpi celesti siano strutture assai comuni lo hanno dimostrato nel 2017 Josè Luis Ortiz Moreno e colleghi dell’Instituto de Astrofísica de Andalucía (CSIC) a Grenada, scoprendo un anello intorno ad Haumea, un pianeta nano che orbita oltre Nettuno, insieme con migliaia di oggetti, chiamati complessivamente oggetti transnettuniani. Haumea è attualmente 50 volte più distante dal Sole di quanto non sia la Terra ed è uno dei più grandi oggetti transnettuniani, anche se è più piccolo di Plutone e del pianeta nano Eris. Haumea è decisamente inusuale, sia per il suo rapido moto di rotazione su se stesso (con un periodo di sole 4 ore circa, che contrasta con il lunghissimo periodo orbitale, di circa 285 anni), sia per la forma molto allungata. Ma a stupire tutti è la presenza di un anello: i dati riguardanti le occultazioni della luce di una stella lontana hanno rivelato una struttura che ha un raggio di 2287 chilometri e uno spessore di 70 chilometri, e giace sul piano equatoriale. Si tratta solo dell'ennesima conferma della genialità di Isaac Newton.

Questo meccanismo è valido anche in prossimità di una stella: non possono esistere pianeti più vicini di 2,5 volte il raggio del loro astro. E per un sistema di stelle doppie? Questo problema fu risolto da Lagrange, lo stesso che individuò i punti lagrangiani (§ 2.9). Entro piccole distanze dal centro di ogni stella, ciascuna delle due mantiene la propria sfera di azione gravitazionale, ma a distanze maggiori le superfici stesse cominciano a deformarsi e, quando entrano in contatto, assumono una struttura ad otto formata da due lobi, che prende il nome di superficie limite di Roche. A distanze ancora maggiori, le stelle agiscono come se fossero una sola. Se ogni componente della stella binaria è all'interno del proprio lobo, non avviene nulla, ma quando una si espande perché diventa una stella gigante o supergigante, e va oltre il punto di contatto tra i due lobi, si avrà un travasamento di materia tra la stella che aumenta il proprio volume e l'altra. Vedremo nel § 5.7 che questo fenomeno può essere collegato all'osservazione dei buchi neri.

Non possiamo chiudere il capitolo delle azioni a distanza senza accennare al meccanismo della fionda gravitazionale o gravity assist. Esso consiste nell'utilizzare la gravità di un pianeta per modificare il percorso e la velocità di un veicolo spaziale. Si può infatti pensare che il modo più semplice per spedire una sonda (o addirittura degli astronauti) dalla Terra ad un pianeta vicino sia quello di far percorrere alla sonda un'orbita ellittica con la Terra al perielio e l'altro pianeta all'afelio: è il cosiddetto "volo di Hohmann", dal nome dell'ingegnere tedesco Walter Hohmann (1880-1945), che lo teorizzò. Questo può funzionare per la Luna, Venere e Marte. Ma se si desiderano raggiungere i pianeti esterni (Giove, Saturno, Urano, Nettuno o i plutoidi, vedi § 5.3), i tempi richiesti sarebbero troppo lunghi, così come la quantità di propellente da impiegarsi per le manovre orbitali. Un calcolo veloce ci dice che l'orbita di Hohmann necessaria per raggiungere Saturno richiederebbe un incremento di velocità di ben 15,7 km/s, del tutto al di fuori delle capacità degli attuali razzi.

L'idea geniale è quella di sfruttare l'enorme gravità di Giove per accelerare le sonde, e lanciarle verso i pianeti più esterni. Fu l'ingegnere russo Yuri Kondratyuk (1897-1942) il primo a suggerire, nel 1919, che un veicolo spaziale interplanetario potesse essere accelerato all'inizio della traiettoria e rallentato alla fine di essa utilizzando la gravità delle lune dei due pianeti; ma il vero padre di questa tecnica fu lo scienziato italiano Giuseppe Colombo (1920-1984). La sua idea è questa: la sonda effettuerà un fly-by (sorvolo) ravvicinato del pianeta gigante, ed allora la gravità del pianeta la attrarrà, aumentando la sua velocità. Dopo aver oltrepassato il pianeta, la gravità continuerà ad attirare il veicolo, rallentandolo. L'effetto sulla velocità, se il pianeta fosse fermo, sarebbe nullo, come risultato della legge di conservazione dell'energia, mentre cambierebbe solo la direzione del veicolo. Teniamo conto però del fatto che i pianeti non sono fermi, ma si muovono nelle loro orbite attorno al Sole. Ne consegue che la velocità della sonda non muta se la si misura in riferimento ad essi, mentre cambia sensibilmente se la si misura rispetto al Sole. Il guadagno di energia cinetica è dovuto al fatto che è il pianeta stesso a perdere parte della sua energia cinetica, rallentando il suo moto di rivoluzione e stringendo la sua orbita, anche se in maniera del tutto impercettibile, vista l'immensa differenza di massa tra Giove e una sonda interplanetaria: il pianeta perde così una quantità minima di energia, lasciando praticamente invariata la propria orbita. A seconda della sua traiettoria, invece, la sonda può guadagnare fino a due volte la velocità orbitale del pianeta! Nel caso di Giove, questa è di oltre 13 km/s: in tal modo, il pianeta "presta" al veicolo una quantità di energia cinetica supplementare, necessaria per raggiungere Saturno usando poco o addirittura nessun combustibile in più di quello usato per raggiungere Giove! Naturalmente questa strategia richiede un'attenta sincronizzazione del lancio con i moti planetari, e per questo la cosiddetta "finestra di lancio" è una fase cruciale per la corretta riuscita della missione.

Naturalmente, non è affatto proibito utilizzare più di una fionda gravitazionale: certo, il viaggio può diventare fastidiosamente lungo, ma ciò diminuisce in modo considerevole il carburante necessario, e permettendo di inviare nello spazio sonde di maggiori dimensioni. Grazie all'opera di Giuseppe Colombo, questa strategia fu utilizzata a bordo delle principali missioni interplanetarie a partire dalla metà degli anni '70, missioni delle quali riparleremo nel § 5.5. Colombo scoprì l'accoppiamento tra rivoluzione e rotazione di Mercurio (il pianeta compie tre rotazioni intorno al proprio asse ogni due rivoluzioni intorno al Sole) e, dopo aver constatato che il periodo dell'orbita della sonda americana Mariner 10 dopo il fly-by di Mercurio sarebbe coinciso con il doppio del periodo di rivoluzione del pianeta stesso, suggerì di sfruttare tale risonanza per programmarne molteplici sorvoli di Mercurio. La sua proposta fu accettata dagli ingegneri della NASA e permise a Mariner 10 (lanciata da Cape Canaveral il 3 novembre 1973 da un razzo Atlas Centaur) di compiere ben tre sorvoli di Mercurio, prima che la sonda esaurisse il propellente. Anche la celeberrima Voyager 2, lanciata da Cape Canaveral il 20 agosto 1977 da un Razzo Titan-Centaur, ha sfruttato un raro allineamento di pianeti per studiare in successione Giove (il 9 giugno 1979), Saturno (il 26 aprile 1981), Urano (il 24 gennaio 1986) e Nettuno (il 25 agosto 1989), utilizzando il gravity assist di ciascun pianeta per farsi scagliare verso il successivo, e inviare a terra una mole monumentale di dati. Infine Cassini-Huygens, che come diremo nel § 5.6 è stata lanciata da Cape Canaveral il 15 ottobre 1997, per raggiungere Saturno ha impiegato quasi sette anni, essendo passata due volte vicino a Venere, poi vicino alla Terra, e infine vicino a Giove, in modo che la grande e pesante sonda potesse raggiungere Saturno con razzi relativamente piccoli!

Il principale limite pratico dell'uso della fionda gravitazionale è la quantità di massa disponibile per ricevere la spinta. Un altro limite è dovuto all'atmosfera del pianeta: più si è vicini al pianeta, maggiore è la spinta che si ottiene. Ma se una sonda è troppo vicina all'atmosfera, l'energia persa per via dell'attrito con questa può essere superiore a quella guadagnata dall'effetto fionda. Questo effetto può tornare utile se invece l'obiettivo è quello di perdere energia per rallentare ed entrare in orbita (il cosiddetto aerofrenaggio).

Una delle frontiere della moderna astrofisica consiste nella ricerca dei pianeti extrasolari, cioè dei pianeti che ruotano intorno a stelle diverse dal Sole. Il primo a postulare la loro esistenza fu lo scienziato medioevale Niccolò Cusano (1401-1464), ma per secoli essi furono solo una congettura, confinata nei telefilm di fantascienza. Solo il 5 ottobre 1995 Michel Mayor e Didier Queloz, dell'Osservatorio di Ginevra, annunciarono di avere scoperto il primo pianeta extrasolare di massa paragonabile a quella di Giove attorno alla stella 51 Pegasi, a 48 anni luce da noi; a partire da allora ne sono stati scoperti oltre 750; l’elenco completo è disponibile su questo sito.

I pianeti extrasolari sono troppo lontani e non abbastanza luminosi per essere osservati mediante un telescopio. Uno dei pochissimi esopianeti osservati in modo diretto è quello indicato con la complicatissima sigla 2M1207B, che orbita intorno alla nana bruna 2M1207, nella costellazione del Centauro, a circa 170 anni luce dalla Terra, ma ciò è reso possibile dalla sua luminosità e dalle sue enormi dimensioni (è 500 volte più grande della Terra). Per individuarli è dunque necessario far ricorso a metodi indiretti. In genere essi ruotano tutti attorno a un principio comune: l’osservazione degli effetti gravitazionali che un pianeta esercita sulla stella attorno a cui orbita.

Uno dei metodi più gettonati è quello astrometrico, consistente nella misurazione precisa della posizione di una stella nel cielo, e nell'osservazione del modo in cui questa posizione cambia nel tempo. Se la stella possiede un pianeta di massa sufficiente, allora la sua azione gravitazionale causerà alla stella un leggero movimento ellittico attorno a un comune centro di massa. Questo movimento può venire determinato mediante osservazioni dirette o tramite l'effetto Doppler: le variazioni nella velocità radiale della stella rispetto alla Terra possono essere dedotte dalle variazioni delle righe spettrali (riparleremo dell’effetto Doppler nel § 7.1). Con questo metodo si può determinare anche la massa del pianeta extrasolare; si è così potuto dedurre che la maggior parte degli esopianeti scoperti è costituita da giganti gassosi molto vicini alla loro stella madre.

Facciamo un esempio. Nel dicembre 2009 gli astrofisici hanno misurato con grande precisione la velocità radiale della stella GJ1214, a 42 anni luce dalla Terra. Il grafico soprastante, nel quale T indica il periodo di rotazione del pianeta, mostra le misurazioni con il relativo margine d’errore. Studiando la curva che meglio approssima i dati (in rosso nel grafico), si è concluso che attorno alla suddetta stella ruota un pianeta battezzato GJ1214b, con una massa pari a 6,55 masse terrestri, con un periodo di 1,58 giorni e con un raggio pari a 2,68 raggi terrestri. Un pianeta di questo tipo è definito "super-Terra", e rappresenta una via di mezzo tra i giganti gassosi e i pianeti rocciosi, di cui riparleremo ampiamente nel § 5.3. Il nostro sistema solare non contiene pianeti di questo tipo, ma è probabile che essi siano assai numerosi nell'universo. Secondo vari studiosi, un tipo molto diffuso di queste super-Terre sarebbe quello dei talassopianeti o pianeti-oceano. Essi si formerebbero ad una distanza dalla loro stella tale che la loro temperatura sia abbastanza bassa per permettere ai composti volatili contenenti idrogeno, come l'acqua, l'ammoniaca e il metano, di raggiungere lo stato di ghiaccio. Questi pianeti sarebbero costituititi da una grandissima quantità d'acqua, che dà vita ad un oceano profondo diverse centinaia di chilometri. Negli strati inferiori di questo immenso oceano l'acqua, per effetto della grandissima pressione, raggiungerebbe lo stato solido, originando un mantello di ghiaccio sopra quello di roccia. Le ultime osservazioni del telescopio spaziale Hubble confermerebbero che GJ1214b è proprio un pianeta con acqua liquida sotto una spessa coltre di vapore: una struttura davvero inusuale e affascinante, che come tante altre è in attesa di ulteriori conferme.

Naturalmente è d'obbligo chiedersi: aver calcolato il lavoro del campo gravitazionale con un procedimento tanto complesso, oltre alla fionda gravitazionale, che utilità posso trarne? Lo saprete passando con me al prossimo capitolo, nel quale introdurremo il concetto di sezioni coniche. Per tornare all'indice, invece, il link è questo.