![]()
|
« Vi fu un momento, poco prima dell'alba, che Lúthien danzava sopra un verde colle... » (QS, cap. XIX) |
Nella lezione precedente ci siamo occupati del moto rettilineo, sia uniforme che uniformemente accelerato; ora vogliamo proseguire nel nostro cammino attraverso la Meccanica, analizzando per la prima volta un moto bidimensionale: il moto dei proiettili, che vedremo essere un moto parabolico. Per questo, partiremo da uno degli episodi più famosi de "Lo Hobbit": l'abbattimento del drago Smaug da parte di Bard l'Arciere.
Anche questi, come altre figure dell'universo tolkieniano, non è stato creato ex novo dal Professore di Oxford, ma è probabilmente ispirato al personaggio di Wiglaf del poema anglosassone "Beowulf", ben conosciuto dal nostro Autore. Come Wiglaf, anche Bard viene introdotto alla fine della storia, è l'unico in grado di abbattere il drago ed è di stirpe regale. Inoltre, secondo John D. Rateliff (1958-), studioso di Tolkien, Bard ha delle analogie con il personaggio di Aragorn: entrambi riconquistano il regno dei propri antenati e diventano re; come Aragorn, anche Bard si avvale di un'arma leggendaria, eredità di un passato regale. Infatti Bard ("barbuto" in antico tedesco), introdotto per la prima volta nel capitolo XIV de "Lo Hobbit", discende da Girion, ultimo re di Dale prima dell'arrivo di Smaug; il suo avo gli ha lasciato in eredità una freccia che non sbaglia mai un colpo. Mentre il drago sta devastando la città di Esgaroth (dopo aver pronunciato le famose, terribili battute "Io sono fuoco! Io sono morte!" con cui si chiude il secondo film della Trilogia Hobbit di Peter Jackson), un tordo ad un tratto si avvicina a Bard e gli indica il punto debole di Smaug. Bard si rende conto con sorpresa che riesce a capire il linguaggio del tordo in quanto discendente dei Re della Valle, e così scaglia la freccia nel punto indicatogli usando il suo grande arco di tasso:
«
Bard tese l'arco al massimo. Il drago tornava volteggiando, volando basso, e
mentre si avvicinava la Luna si levò sopra la riva orientale e inargentò le
sue grandi ali.
"Freccia!" disse l'arciere. "Freccia nera! Ti ho conservata per ultima. Non mi hai mai tradito e io ti ho sempre recuperata. Ti ho avuto da mio padre ed egli ti ebbe dai suoi antenati. Se veramente provieni dalla fornace del vero Re sotto la Montagna, va' ora dritta al bersaglio, e buona fortuna!"
Il drago piombò ancora una volta più in basso che mai e, mentre virava e si
tuffava giù, il suo ventre brillò bianco per la luce scintillante delle
gemme sotto la luna, tranne che in un punto. Il grande arco vibrò. La freccia
nera schizzò via dalla corda, puntando diritta alla zona scoperta sulla
sinistra del petto, dove la zampa anteriore si scostava di molto dal corpo.
Lì si conficcò e sparì, punta, asta e piuma, tanto fiero era stato il suo
volo. Con un grido stridente che assordò gli uomini, abbatté gli alberi e
spaccò le pietre, Smog sobbalzò schiumando nell'aria, si capovolse e si
schiantò rovinando al suolo. Tutt'intero cadde sulla città. I suoi ultimi
spasimi la distrussero completamente in uno scoppio di scintille e schegge
volanti. Il lago vi precipitò sopra ruggendo. Un'enorme massa d'acqua si
sollevò, bianca sotto la Luna nel buio improvviso. Ci fu un sibilo, un
vortice ribollente, e poi silenzio. E questa fu la fine di Smaug e di Esgaroth.
»
(Lo Hobbit, cap. XIV)
Bard si trova al suolo, quindi possiamo porre l'origine di un sistema di riferimento cartesiano nell'esatto punto in cui egli scocca la freccia nera; l'asse delle ascisse sarà parallelo al suolo, quello delle ordinate sarà perpendicolare ad esso, e il piano xy così ottenuto contiene al suo interno la traiettoria della freccia, per cui anche Smaug dovrà trovarsi in un punto opportuno di tale piano. Cerchiamo di descrivere la traiettoria della freccia.
Quest'ultima parte con velocità v0 inclinata di un angolo α rispetto al suolo, detto angolo di alzo. La velocità v0 può perciò essere scomposta in due componenti, che diremo v0x e v0y, il primo orizzontale e il secondo verticale. In base alle regole della trigonometria, si sa che:
Vi è anche un'accelerazione cui la freccia è soggetta: è quella di gravità, ed è diretta verso il basso. In altre parole essa non ha alcuna componente lungo x, e l'unica componente non nulla è interamente diretta lungo il semiasse negativo delle y. Ma allora il moto lungo la x è rettilineo uniforme, non essendovi alcuna componente dell'accelerazione in quella direzione, mentre quello lungo la y è uniformemente accelerato, con velocità iniziale diretta verso l'alto ed accelerazione diretta verso il basso. In base a quanto abbiamo detto nella lezione precedente, le due leggi orarie risulteranno perciò le seguenti:
Sostituiamo le (1) nelle (2) ed otteniamo:
Queste sono le equazioni parametriche del moto della freccia, nelle quali l'ascissa x e l'ordinata y sono espresse in funzione del tempo t. Per ottenere l'equazione cartesiana del moto, occorre eliminare il parametro t. A questo scopo ricaviamo dalla prima delle (3) t = x / v0 cos α e sostituiamola nella seconda. Il risultato è:
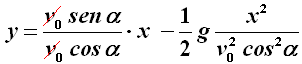
che si può riscrivere:
Come si vede, si tratta dell'equazione di una parabola, essendo del tipo y = a x2 + b x + c. Essendo il termine noto c uguale a zero, la parabola passa per l'origine, e ciò è sensato, in quanto è dall'origine che parte la freccia del nostro eroe Bard. Determiniamo inoltre la derivata della (4):
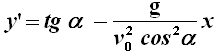
Essa ci dice in ogni punto qual è la pendenza della traiettoria, cioè il coefficiente angolare della tangente. Ponendo in essa x = 0, si ha y' = tg α. Noi sappiamo che il coefficiente angolare di una retta esprime la tangente trigonometrica dell'angolo che essa forma con il semiasse positivo delle x, e dunque la tangente alla traiettoria nell'origine ha proprio pendenza pari ad α. Ciò significa che è tangente alla velocità iniziale v0, il che è proprio quanto ci aspettavamo dalla traiettoria della nostra freccia. Ecco come risulta, rappresentandola in coordinate cartesiane ortogonali:

Si noti che la distanza tra il punto in cui la freccia viene lanciata e quella in cui raggiunge il bersaglio si chiama gittata della freccia. Se Smaug vola così basso da poter essere ritenuto radente al suolo, allora la gittata può essere trovata intersecando l'equazione (4) della traiettoria con la retta y = 0, cioè con l'asse x. Con semplici calcoli si ottiene che tale gittata misura:
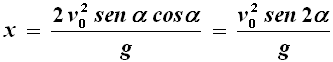
Il massimo della gittata si ha quando è massimo il sen 2α, e siccome il seno è massimo (e vale + 1) per 2α = π/2, se ne conclude che la gittata massima corrisponde ad un alzo di α = π/4, cioè di 45°. Ne sa qualcosa la rana, che infatti cerca sempre di saltare con un angolo di 45°, per massimizzare la gittata del salto a parità di energia spesa.
L'altezza massima raggiunta dalla freccia, come si vede in figura, coincide con il vertice della parabola. E siccome la parabola è simmetrica, per ottenere l'ordinata di tale vertice basterà sostituire nella (4) la metà esatta della gittata, cioè v02 sen α cos α / g. Si ottiene facilmente come risultato:
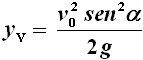
In corrispondenza di α = 45°, tale altezza vale v02 / 4 g. Il tempo di volo è invece il tempo necessario per percorrere l'intera gittata, e si può ottenere dividendo la gittata per la componente v0x della velocità. Il risultato è:
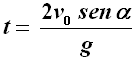
Se invece Smaug vola ad un'altezza h rispetto al livello al quale si trova Bard, occorrerà intersecare la (4) con la retta y = h. Supponiamo per esempio che Smaug voli ad un'altezza di 15 metri e il punto scoperto della sua corazza disti 10 metri da Bard lungo l'orizzontale; ciò significa che la parabola dovrà passare per il punto di coordinate ( 10 ; 15 ). Ora, un arco pesante 65 libbre può imprimere alla freccia una velocità di 75 metri al secondo, dunque v0 = 75. Sostituendo questi dati nella (4) si ha:
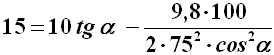
Dopo alcuni passaggi, usando le regole della trigonometria, si perviene all'equazione:
0,087 tg2 α – 10 tg α + 15,087 = 0
le cui soluzioni sono tg α1 = 113,26 e tg α2 = 1,53. Il primo valore fornisce α1 = 89° 29' 39", il secondo invece restituisce α2 = 56° 48' 57". Sostituiamo α1 nella (4) e troviamo l'equazione della traiettoria T:
T1) y = 113,26 x – 11,175 x2
Questa parabola ha il vertice in ( 5,1 ; 286,9 ). Sostituendo invece α2 nella stessa equazione si trova:
T2) y = 1,53 x – 0,0029 x2
Essa invece ha il vertice in ( 263,8 ; 201,8 ). Quale delle due equazioni è quella giusta? Apparentemente entrambe, poiché il punto ( 10 ; 15 ) soddisfa sia la T1 che la T2: sostituendo in entrambe x = 10 si ricava y = 15. Se le rappresentiamo in un diagramma cartesiano ortogonale, tuttavia, troveremo due traiettorie ben differenti tra di loro, come si vede qui sotto (in ascisse e in ordinate non è stata usata la stessa scala):
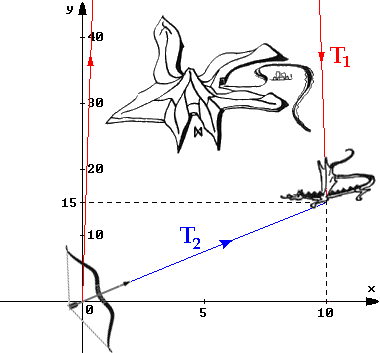
Appare evidente che la traiettoria corretta è la T2 (in blu), poiché seguendola la freccia di Bard colpisce il drago Smaug da sotto, come descritto ne "Lo Hobbit", mentre se seguisse la T1 (in rosso) il dardo dovrebbe colpire il mostro solo ricadendo dall'alto, e in quel caso l'arciere non potrebbe mirare ad un ipotetico punto debole posto sul dorso del dragone. Si osservi che, nel caso della T2, la componente orizzontale della velocità della freccia infallibile è pari a 75 x cos (56° 48' 57") = 22,4 m/s; il tempo di volo necessario alla freccia per colpire Smaug è allora pari a 10 m / 22,4 m/s = 0,44 secondi. Invece, nel caso della traiettoria T1 la componente orizzontale della velocità sarebbe pari a 75 x cos (89° 29' 39") = 0,029 m/s, e il tempo di volo salirebbe a 10 m / 0,66 m/s = 33,95 s; decisamente troppo, per riuscire a colpire il drago Smaug. Non c'è dubbio, Bard meritava davvero di diventare Re di Dale, dopo essere riuscito a centrare un così ristretto punto della corazza di Smaug con una precisissima traiettoria della sua freccia nera!

Oltre al moto parabolico, nel Legendarium di Tolkien vi sono riferimenti ad un altro importantissimo tipo di moto, il moto circolare uniforme? Indirettamente, sì: nel VI volume della History of Middle Earth, inedito in Italia, in occasione della sua Festa d'Addio, Bilbo regala un orologio alla cugina Caramella Paffuti. Quale il motivo?
«
Caramella, sebbene poco puntuale, era stata una cugina piuttosto gradita, finché un giorno, arrivata tardi per il tè, aveva dichiarato che l'orologio di Bilbo era in avanti: gli orologi di Bilbo erano sempre puntuali ed egli non si scordò il
fatto... »
(HoME VI, 15, 17, 32)
Le lancette dell'orologio effettivamente si muovono di moto circolare uniforme. Ma non è di questo che ora vogliamo parlare, poiché si tratta in effetti di un riferimento piuttosto debole al moto circolare uniforme. Ve ne è però un altro, ed è quello che ha dato il titolo a questa lezione. Infatti la più grande di tutte le storie d'amore della Terra di Mezzo, quella fra il mortale Beren e l'elfa Lúthien, ebbe inizio quando il figlio di Barahir la vide per la prima volta, mentre danzava nei boschi di Neldoreth:
«
Aggirandosi d'estate nei boschi di Neldoreth, Beren si imbatté in Lúthien, figlia di Thingol e Melian, ed era sera, nel momento in cui la luna saliva in cielo, e
Lúthien danzava sull'erba sempre verde nelle radure lungo le rive dell'Esgalduin. Ed ecco il ricordo di tutte le sue sofferenze abbandonò Beren, ed egli cadde in preda ad un incantesimo, poichè
Lúthien era la più bella di tutti i figli di
Iluvatar. [...] Ma Lúthien scomparve alla vista di Beren, il quale divenne sordo come chi sia in preda d'incantesimo, e a lungo s'aggirò per i boschi, selvaggio e vigile come una belva, cercandola. In cuor suo la chiamava
Tinúviel, che significa Usignolo, come vien detta nella lingua degli Elfi Grigi questa figlia del crepuscolo, perché non sapeva quale altro nome darle. E la scorgeva lontano come foglia ai venti d'autunno e, d'inverno, una stella sopra un colle, ma una catena gli gravava le membra.
Vi fu un momento, poco prima dell'alba, la vigilia di Primavera, che Lúthien danzava sopra un verde colle; e d'un tratto prese a cantare. Acuto tanto da trapassare il cuore era il suo canto, simile a quello dell'allodola che si leva dalle porte della notte e riversa la propria voce tra le stelle morenti, lei che scorge il sole dietro le mura del mondo; e il canto di
Lúthien sciolse i vincoli dell'inverno, e le acque gelate parlarono e i fiori balzarono su dalla fredda terra là dove si erano posati i suoi piedi.
Allora Beren fu liberato dall'incantesimo del silenzio, ed egli la chiamò, invocando
Tinúviel; e i boschi
echeggiarono del nome. Lúthien si arrestò meravigliata e più non fuggì, e Beren venne a
lei. Ma, non appena gli posò gli occhi addosso, cadde preda della sorte e si
innamorò di lui. »
(QS, capitolo XIX)

Ted Nasmith, Lúthien Tinúviel (1990)
Il nome di Lúthien probabilmente deriva dall'antico inglese Luvien, "amore". E mai etimologia fu più azzeccata, visto che Beren si innamorò perdutamente di lei, come si evince dal brano testé letto. E, come mostra chiaramente il dipinto del grande Ted Nasmith qui sopra riprodotto, l'uomo si innamorò dell'elfa mentre ella danzava roteando su se stessa, come fanno le più grande ballerine classiche del nostro mondo. E questo ci introduce al discorso circa la conservazione del momento angolare.
Consideriamo infatti un sistema formato da un corpo di massa m che descrive un'orbita circolare di raggio r intorno ad un punto C con una velocità costante v. Ovviamente v è un vettore in ogni punto tangente alla traiettoria circolare; la sua quantità di moto o momento lineare è p = m v. Si definisce momento della quantità di moto o momento angolare il vettore:
![]()
dove r è il vettore posizione della massa m rispetto al centro C. In altre parole, il momento della quantità di moto è dato dal prodotto vettoriale tra il vettore posizione del corpo in rotazione e il vettore quantità di moto. Per definizione di prodotto vettoriale, la sua direzione è perpendicolare al piano individuato dai vettori r e p, cioè al piano nel quale avviene la rotazione del corpo, mentre la sua direzione è data dalla regola della mano destra: se le dita della mano destra ruotano nella direzione del corpo, il momento angolare segue il verso del pollice. Le sue dimensioni fisiche sono:
[ L ] = [ m v r ] = [ Kg m s–1 m ] = [ m2 Kg s–1 ]
Il momento angolare perciò si misura di solito in J s. Il modulo di tale vettore è dato da:
L = r p sen α = m v r sen α
Nel caso di moto circolare uniforme, l'angolo tra il vettore posizione r e la velocità tangenziale v vale 90°, e il seno di 90° vale 1, perciò L = m v r. Ora, nel moto circolare uniforme la velocità tangenziale v è pari alla velocità angolare ω per il raggio r, per cui la precedente diventa:
L = m ω r2
Dimostriamo adesso che, se non vi è alcun momento esterno applicato al sistema, cioè se il sistema è isolato, il momento angolare si conserva. Se r è costante (affermazione vera nel caso di moto circolare), la variazione ΔL del momento della quantità di moto nel tempo Δt è pari a:
![]()
e dividendo entrambi i membri per Δt:
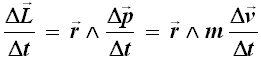
ma Δv/Δt, come si sa, è l'accelerazione a:
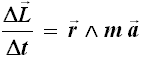
Per il Secondo Principio della Dinamica, F = m a, per cui la precedente può essere riscritta:
dove Fext sono le forze esterne applicate al sistema, ed Mext sono i momenti esterni applicati al sistema. Questa viene chiamata la Seconda Equazione Cardinale della Dinamica, ed afferma che i momenti delle forze esterne che agiscono su di un sistema provocano una variazione nel tempo del momento della quantità di moto (per inciso, la Prima Equazione Cardinale della Dinamica afferma invece che le forze esterne che agiscono su di un sistema provocano una variazione nel tempo della quantità di moto del sistema). Se Mext = 0, ovviamente, dalla precedente di ricava che ΔL/Δt = 0, cioè che il momento angolare è costante nel tempo. Abbiamo così dimostrato quello che viene universalmente conosciuto come Principio di Conservazione del Momento Angolare: se un sistema è isolato, cioè se su di esso non sono applicati momenti esterni, il momento angolare resta costante.
È questo il risultato che ci interessa, ai fini della nostra discussione sulla danza di Lúthien che fece innamorare l'eroico Beren. Supponiamo infatti che la figlia di Re Thingol Mantogrigio rotei su se stessa con le braccia aperte, come mostra la pregevole opera di Ted Nasmith sopra riprodotta. Sia m la massa di Lúthien, ωi la sua velocità angolare iniziale e ri la distanza della punta delle sue dita all'asse attorno alla quale ruota. Inizialmente la sua quantità di moto sarà m ωi ri2. Immaginiamo ora che l'elfa chiuda le braccia; la distanza del suo punto più lontano dall'asse di rotazione si ridurrà ad rf, ed allora anche la sua velocità angolare ωf cambierà. In base al Principio di Conservazione del Momento Angolare, valido se si ritiene Lúthien un sistema isolato (la sua forza peso è controbilanciata dalla reazione vincolare del terreno), avremo che:
m ωi ri2 = m ωf rf2
La massa m si può semplificare, ed allora giungiamo alla conclusione che, diminuendo r, ω dovrà per forza aumentare, altrimenti L non sarà più costante. Insomma, chiudendo le braccia Lúthien girerà più veloce attorno al proprio asse, come ben sa chi oggi pratica danza classica. Supponiamo ad esempio che essa volteggi su se stessa compiendo un giro al secondo, e con le braccia distese in modo che ri = 72 cm. Allora ωi vale 2π radianti al secondo, cioè 6,28 rad/s. Se la ragazza chiude le braccia in modo che rf = 48 cm, la precedente fornisce l'equazione:
6,28 rad x (0,72 m)2 = ωf x (0,48 m)2
da cui si ricava ωf = 16 rad/s circa, il che equivale più o meno a due giri e mezzo al secondo.
Naturalmente qualcuno di voi potrà obiettarmi; ma la (5) la abbiamo ricavata per un corpo puntiforme, mentre la bellissima Lúthien è un corpo esteso. Vero: vale perciò la pena di aggiungere due parole in proposito. Tanto per cominciare, dobbiamo supporre che le membra dell'elfa restino equidistanti tra loro durante la rotazione sul proprio asse. Ciò vuol dire che consideriamo la nostra eroina come un corpo rigido, ovvero come un corpo indeformabile. Un ottimo modello di corpo rigido nel mondo di Tolkien potrebbe essere l'Unico Anello, un oggetto del quale riparleremo più avanti per l'invisibilità che esso dona, ma che tra le altre sue qualità ha quella di non poter essere deformato, e quindi distrutto, neanche prendendolo a martellate, come rivela questo colloquio tra Frodo e Gandalf, prima che l'avventura abbia inizio:
«
"Ma perchè non distruggerlo? Dici che lo si sarebbe dovuto fare già da
molto tempo: perchè non farlo ora?" gridò Frodo. "Se mi avessi
avvertito o magari mandato un messaggio, me ne sarei certo disfatto!"
"Veramente? E in che modo? Ci hai mai provato?"
"No, ma suppongo si possa martellare o fondere..."
"Benissimo, allora provaci!" disse Gandalf. "Provaci
subito!" [...] Gandalf rise sardonicamente:
"Lo vedi? Si sta impadronendo di te, e anche tu, Frodo, già non riesci a
sbarazzartene, e non hai più la volontà di distruggerlo. Ma quanto a rompere
l'Anello, la forza è del tutto vana. Anche colpendolo con una mazza da
fabbro, non lo scalfiresti nemmeno. Le tue mani e le mie mai lo potranno
disgregare. [...] Nessun fabbro e nessuna fucina in tutta la Contea sarebbe in
grado di alterarlo. Nemmeno le fornaci e le incudini dei Nani vi
riuscirebbero. »
(SdA, libro I, cap. II)
Come l'Unico Anello, che non può essere annientato da nessuna delle arti di Uomini, Elfi, Nani e Hobbit, esiste solo nella mente di Tolkien, in realtà anche il corpo rigido è un'astrazione, poiché nessun oggetto del nostro mondo è tale, che le singole parti che lo compongono abbiano distanze fisse le une dalle altre. Ipotizziamo però che il corpo di Lúthien di Doriath sia davvero composto di N elementi piccolissimi, ciascuno dei quali sia assimilabile ad un punto materiale, immobile rispetto a tutti gli altri; possiamo ad esempio pensare a tali elementi come agli atomi che costituiscono il corpo dell'eroina elfica. Consideriamo l'i-esimo di questi N elementini (con i che va da 1 ad N) e supponiamo che abbia massa mi, distanza dall'asse di rotazione ri e velocità angolare ω; quest'ultimo valore sarà lo stesso per tutti gli N elementi, anche se ognuno ha velocità tangenziale vi diversa da quelle degli altri. Ognuno allora avrà momento angolare Li = mi ω ri2.
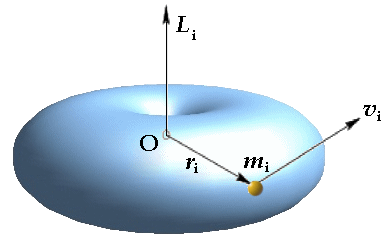
Siccome tutti questi momenti sono diretti lungo l'asse di rotazione e rivolti verso l'alto (se Lúthien rotea in senso antiorario) o verso il basso (se rotea in senso orario), il modulo del momento angolare totale sarà pari alla somma scalare di tutti gli N moduli testé scritti:
Ltot = m1 ω r12 + m2 ω r22 + m3 ω r32 + ... + mN ω rN2
raccogliamo a fattor comune ω:
Ltot = ω ( m1 r12 + m2 r22 + m3 r32 + ... + mN rN2 )
Tra parentesi abbiamo una grandezza nuova, ottenuta dalla sommatoria dei prodotti fra le masse di ogni elementino e i quadrati delle loro distanze dall'asse di rotazione. Tale sommatoria è tanto maggiore quanto più lontane arrivano le masse dall'asse di rotazione stesso; inoltre, come il momento lineare o quantità di moto si ottiene dal prodotto tra la velocità lineare e la massa del corpo (p = m v), così il momento angolare o momento della quantità di moto si ottiene moltiplicando la velocità angolare per questa sommatoria, che possiamo così considerare l'equivalente della misura dell'inerzia del corpo nel moto rotatorio (infatti la massa misura l'inerzia del corpo nel moto traslatorio). Per questo tale sommatoria viene chiamata momento d'inerzia I del corpo rigido:
Il momento d'inerzia si misura in metri quadrati per chilogrammo, ed è tanto maggiore quanto maggiore è la distribuzione delle masse intorno all'asse di rotazione, cioè quanto maggiori sono le distanze di esse dall'asse di rotazione. Grazie ad esso si può esprimere in maniera semplicissima il momento angolare di un corpo rigido, come ad esempio la Principessa Lúthien che balla:
Ltot = ω I
Sempre utilizzando il momento d'inerzia, è possibile scrivere la formula dell'energia cinetica di un corpo rigido che ruota. Infatti l'energia cinetica è una grandezza scalare, dunque il totale è pari alla somma di tutte le energie cinetiche degli N elementini che compongono il corpo:
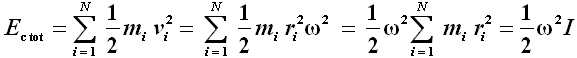
Basta infatti ricordare che vi = ω ri e mettere a fattor comune 1/2 ω. Mentre l'energia cinetica traslazionale si ottiene moltiplicando la massa (cioè l'inerzia) per la velocità lineare al quadrato e dividere il risultato per 2, l'energia cinetica rotazionale si ricava moltiplicando il momento d'inerzia per la velocità angolare al quadrato e dividendo il tutto per 2: il parallelo è perfetto.
Questo vale se il corpo rigido è formato da un insieme discreto di N masse. Ma se si tratta di un corpo continuo? Il calcolo allora diventa difficile, perchè bisogna fare ricorso ad un integrale. Supponiamo di dividere il corpo in infinite masse infinitesime dm, ciascuna delle quali ha una distanza R dal centro. Nella (6) allora la sommatoria si trasforma in una somma integrale estesa a tutto il corpo:
Si consideri ad esempio un disco (o un cilindro) omogeneo di massa M e raggio R che ruota intorno al proprio asse di simmetria. Come si vede nella figura a fianco, esso può essere immaginato composto di infinite corone circolari concentriche di raggio r e spessore infinitesimo dr. Quanto vale la massa infinitesima dm di ogni corona circolare? La sua area dA può essere espressa da 2 π r dr (circonferenza per lo spessore), e la densità del disco è pari a M/π R2 (la massa divisa per l'area totale), per cui avremo:
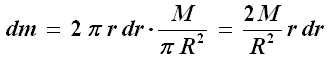
Sostituendo nell'integrale (7) si ottiene così:
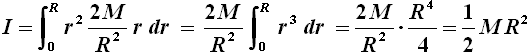
Dunque l'inerzia di un disco (o di un cilindro) rispetto al suo asse di simmetria si ottiene moltiplicando la sua massa per il suo raggio al quadrato, e dividendo il risultato per 2. Con calcoli analoghi, solo molto più complessi, è possibile ottenere i momenti d'inerzia di tutte le principali figure solide. Eccole riassunte in uno specchietto semplificato:
Ad esempio, la bella Lúthien che balla roteando su se stessa con le braccia strette contro il corpo è assimilabile ad un cilindro di massa M e raggio R, per cui rientra nel terzo caso dello schema soprastante, mentre se rotea con le braccia distese in orizzontale bisognerà sommare al momento d'inerzia del cilindro cui assimiliamo il suo corpo il momento d'inerzia dell'asse rappresentato dalle sue braccia, calcolabile tramite il sesto caso riportato nello specchietto.
E se il cilindro ruotasse attorno ad un asse diverso da quello passante per l'asse di simmetria? Si può dimostrare che vale il Teorema di Steiner, così detto in onore del matematico svizzero Jakob Steiner (1796-1863):
![]()
Esso afferma che il momento d'inerzia di un corpo in rotazione attorno ad un asse parallelo a quello passante per il suo baricentro G si ottiene sommando al momento d'inerzia rispetto a quell'asse baricentrale (qui indicato con la dicitura IG) il prodotto tra la massa del corpo e il quadrato della distanza d fra i due assi. Ad esempio, se il cilindro non ruota intorno all'asse baricentrale ma attorno ad una delle sue generatrici, la distanza tra questa e l'asse passante per il baricentro è pari al raggio R, e quindi per il Teorema di Steiner si ha:
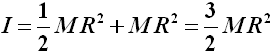
Questo risultato è maggiore del precedente (per la precisione triplo), perchè nel caso della rotazione intorno all'asse del baricentro, la massa di Lúthien Tinúviel è equamente distribuita attorno ad esso, mentre se ella ruota intorno ad un asse eccentrico, la sua massa si trova mediamente molto più distante da tale asse!

Passiamo ora ad un nuovo argomento, riguardante la Statica dei Fluidi. Prima di lasciare del tutto i corpi rigidi per passare a quelli liquidi ed aeriformi però dobbiamo introdurre una nuova grandezza fisica, la pressione. Per questo, faremo riferimento ad un celeberrimo episodio de "Lo Hobbit", all'inizio del viaggio dei nostri eroi verso la Montagna Solitaria: avvistato un fuoco tra gli alberi, Thorin e compagni mandano Bilbo in avanscoperta ad appurare di cosa si tratta, e lo Hobbit scopre che il fuoco è stato acceso da tre Troll (detti anche Uomini Neri), rispondenti ai nomi di Berto, Maso e Guglielmo Huggins, i quali prima catturano Bilbo e poi tutti i Nani corsi in suo aiuto. Dopo averli legati, dentro dei sacchi, i tre Troll si mettono a discutere se arrostirli lentamente, tritarli finemente e bollirli, oppure schiacciarli uno per uno sedendosi sopra di essi!
«
"Chiudi il becco!" disse Maso, che pensava fosse stata la voce di
Guglielmo. "Chi è che discute, a parte te? Vorrei proprio saperlo!"
"Sei uno zoticone!" disse Guglielmo.
"Zoticone sarai tu!" disse Maso. E così la discussione ricominciò
da capo e si fece più violenta che mai, finché alla fine decisero di sedersi
sui sacchi l'uno dopo l'altro e di schiacciare i Nani e bollirli alla prossima
occasione. »
(Lo Hobbit, cap. II)

I Tre Uomini Neri nella trilogia dedicata a "Lo Hobbit" da Peter Jackson
È qui che entra in gioco la pressione. Si definisce pressione P il rapporto tra la forza F che preme perpendicolarmente ad una superficie e l'area S di tale superficie:
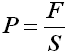
Si tratta di una grandezza scalare, tanto maggiore quanto maggiore è la forza premente e quanto minore è l'area su cui la forza agisce. Se Berto, Maso e Guglielmo si sdraiano per terra con tutta la superficie del corpo, la loro forza peso si distribuisce su una vasta superficie, e dunque la pressione è relativamente bassa. Se invece si siedono su un sedile, come volevano fare con i sacchi in cui erano legati i Nani, il loro peso è concentrato su di una superficie assai più ristretta, e dunque la pressione da loro esercitata è assai maggiore, e quindi più letale.
L'unità di misura della pressione nel Sistema Internazionale è il Pascal, indicato con Pa, in onore del fisico e filosofo francese Blaise Pascal (1623-1662). Esso è definito come la pressione esercitata dalla forza di un Newton applicata perpendicolarmente alla superficie di un metro quadrato:
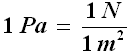
Esistono però moltissime altre unità di misura della pressione, la più famosa delle quali è l'atmosfera. Infatti anche l'atmosfera che circonda il pianeta Terra viene attirata dalla forza di gravità, e dunque ha un peso: se non ne avesse, tenderebbe ad espandersi come tutti i gas e sfuggirebbe al pianeta, disperdendosi nello spazio. A causa del suo peso, l'atmosfera esercita una pressione chiamata pressione atmosferica su tutti gli oggetti che sono immersi in essa. Tale pressione si esercita ugualmente su tutte le superfici in tutte le direzioni (è il Principio di Pascal: la pressione esercitata in un punto qualsiasi di un fluido si esercita con la stessa intensità su qualsiasi superficie a contatto con il fluido, comunque sia orientata), e la sua grande entità fu dimostrata nel 1654, durante la Dieta Imperiale di Ratisbona, dal fisico tedesco Otto von Guericke (1602-1686): alla presenza dell'imperatore Ferdinando III d'Asburgo egli prese due emisferi cavi in bronzo del diametro di un metro, li fece combaciare e con una macchina pneumatica di sua invenzione praticò il vuoto dentro di essi. Neppure 30 cavalli, che tiravano gli emisferi da parti opposte, riuscirono a separarli! Tale esperimento passò alla storia con il nome di Emisferi di Magdeburgo, città nella quale von Guericke era nato e della quale era borgomastro.
La misura dell'entità della pressione atmosferica fu effettuata per la prima volta dal fisico italiano Evangelista Torricelli (1608-1647), discepolo di Galileo Galilei, con un esperimento altrettanto celebre quanto quello di Otto von Guericke. Egli prese una cannula di vetro lunga circa un metro e chiusa ad un'estremità, e la riempì di mercurio fino all'orlo; tappò l'altra estremità con un dito e la capovolse in una bacinella piena anch'essa di mercurio. Ci si aspetterebbe che il tubo si svuoti completamente; invece, la colonna di mercurio scese fino ad un'altezza di 760 millimetri. Infatti la pressione atmosferica, che si esercita sulla superficie libera del mercurio nella bacinella, si trasmette all'interno del mercurio e controbilancia la pressione del mercurio rimasto dentro al tubo. Torricelli aveva realizzato il primo barometro, cioè il primo strumento in grado di misurare la pressione atmosferica. Forse non lo sapevate, ma in occasione della sua famosissima Festa d'Addio alla Contea, Bilbo Baggins ha lasciato in dono proprio un barometro al suo parente Colombo Soffiatromba, dimostrando che questo strumento, forse di origine Númenoreana, era ben noto nel mondo di Tolkie. E il barometro era accompagnato da questa dedica:
«
"Per Colombo
Soffiatromba, trattalo a modo tuo". Infatti Colombo era solito colpirlo violentemente con il suo grande dito paffuto ogni volta in cui veniva a trovare
Bilbo: aveva timore di bagnarsi e tutto l'anno indossava sciarpa ed
impermeabile. »
(HoME
VI, 15, 17, 32)
Sia h l'altezza della colonna di mercurio ed S l'area della sezione della cannula. Allora il volume del mercurio in essa presente è V = h S. Detta ρ la densità del mercurio, se ne deduce che la sua massa è m = ρ V = ρ h S. Il suo peso invece è m g = ρ g h S. Ne consegue che la pressione esercitata sul fondo della cannula è data da P/S = ρ g h; questa è quella che è conosciuta come Legge di Stevin, dal nome del fisico fiammingo Simon Stevin (1548-1620). La densità del mercurio vale ρ = 13.600 Kg/m3, dunque la pressione sul fondo della colonnina di mercurio è P = 13.600 Kg m–3 x 9,8 m s–2 x 0,76 m = 101.325 Pa. Questo valore è pari alla pressione atmosferica al livello del mare, e viene utilizzata come unità di misura, chiamata un'atmosfera (atm). Un'atmosfera è pari anche a 760 millimetri di mercurio (mm Hg); la pressione di una colonnina di mercurio alta un millimetro viene chiamata un torr, in onore di Torricelli. Ne consegue che 1 atm = 760 torr, e quindi 1 torr = 101.325/760 = 133,3 Pa. Il torr è usato in particolare per misurare la pressione sanguigna per mezzo di uno strumento chiamato sfigmomanometro. Se al posto del mercurio utilizzassimo acqua, la colonna risulterebbe alta 101.325/(9,8 x 1000) = 10,33 metri. Il millimetro d'acqua invece, per la legge di Stevin, vale 1.000 Kg m–3 x 9,8 m s–2 x 10–3 m = 9,8 Pa. Altre unità di misura della pressione sono l'atmosfera tecnica, pari a 10.000 mm di acqua, cioè a 98.000 Pa, e il bar, pari a 100.000 Pa. In particolare un sottomultiplo del bar, il millibar (10–3 bar), viene utilizzata in meteorologia; la pressione a livello del mare è pari a 1013 millibar. Oggi l'Unione Europea ha messo al bando tutte le unità non appartenenti al S.I., per cui al posto del millibar si usa l'ettoPascal, visto che 1 bar/1000 = 100.000 Pa/1000 = 100 Pa = 1 hPa.
Quale pressione potrebbero dunque esercitare i tre Uomini Neri, se si sedessero davvero sopra i poveri Nani? Tutto dipende dalla loro massa, che va stimata. Tanto per cominciare, Berto, Maso e Guglielmo sono alti circa 12 piedi, cioè tre metri e sessanta centimetri. Facciamo ora ricorso all'indice di massa corporea (o BMI, dall'inglese Body Mass Index), definito come il rapporto tra la massa e il quadrato dell'altezza di un individuo. Un uomo di corporatura normale (né obeso né scheletrico) dovrebbe avere un indice di massa corporea compreso tra 18 e 25, ma la rappresentazione dei Troll che ne dà la Trilogia de "Lo Hobbit" di Peter Jackson li fa somigliare invece ad esseri umani particolarmente tozzi ed obesi, come si vede dal fotogramma soprastante, per cui possiamo assumere per loro un BMI = 50. Allora un soggetto alto tre metri e sessanta e con questo BMI dovrebbe avere una massa pari a 50 x ( 3,60 )2 = 648 Kg. Ora, la densità media del corpo umano è circa di 980 kg/m3, il che ci porta ad un volume di 648 Kg / 980 kg/m3 = 0,66 m3. Siccome si tratta di Troll di Pietra, si può pensare che essi abbiano la densità del granito, cioè pari a 2.750 kg/m3. Ciò ha come conseguenza una massa di 0,66 m3 x 2.750 kg/m3, cioè di circa 1818,4 Kg, ed un peso di 1818,4 Kg x 9,8 m s–2 = 17.820 Newton. Su quale superficie si distribuisce questo peso? Un Nano è alto mediamente 1,50 cm, per cui possiamo pensare che la sezione del sacco che lo contiene sia pari a circa 500 cm2. Allora la pressione su ogni Nano equivarrebbe a 17.820 N/0,5 m2 = 35.640 Pa. Si tratta del 35 % di un'atmosfera, e quindi di una pressione considerevole, più che sufficiente per ridurre i Nani in gelatina, come concertano di fare i tre Troll, sicuramente massicci e dotati di una forza fuori dal comune, ma altrettanto ottusi e lenti di comprendonio, tanto che Gandalf può facilmente abbindolarli, facendoli litigare fra di loro finché il Sole non sorge e non li tramuta nella pietra con cui l'Oscuro Signore li aveva creati!

Ma vi è un altro episodio del Legendarium di Tolkien, e stavolta nel "Signore degli Anelli", che riguarda da vicino il problema della pressione; mi riferisco alla camminata dell'Elfo Legolas. Tra le altre qualità che il figlio di Thranduil possiede si annoverano i riflessi velocissimi, la vista acutissima (di questo argomento riparleremo in una futura lezione), un udito supersensibile, percezioni sensoriali sviluppatissime e, last but not least, ha anche un passo leggerissimo: non fa rumore neanche mentre corre e riesce a camminare sulla neve alta e fresca senza sprofondarvi, come dimostrano questo passo della "Compagnia dell'Anello", nel quale i nove compagni tentano inutilmente di attraversare il Passo Cornorosso sotto una fitta tempesta di neve, e il relativo fotogramma tratto dall'omonimo film di Peter Jackson:
«
Si misero in marcia lentamente, e poco dopo avanzavano con fatica. In alcuni
punti la neve arrivava al petto, e pareva allora che Boromir stesse nuotando o
scavando con le sue grandi braccia, anziché camminare.
Legolas li osservò qualche istante con il sorriso sulle labbra, quindi si
rivolse agli altri. "I più forti devono cercare una via, dite voi? Ma io
dico: fate arare il campo al coltivatore, ma scegliete una lontra per nuotare,
e per correre veloce su erbe e foglie, o sulla neve... un Elfo."
Dicendo ciò, balzò agilmente avanti; ed allora Frodo si accorse per la prima
volta, benché da tempo lo sapesse, che l'Elfo non portava stivali, bensì
scarpe leggere come al solito, che lasciavano poche tracce sulla neve.
"Addio!" disse a Gandalf. "Io vado a cercare il sole!"
Scattò veloce come un corridore su terreno solido, ed avendo raggiunto
rapidamente gli uomini che avanzavano a stento, li sorpassò, agitando la mano
in segno di saluto, proseguì correndo lontano e scomparve dietro il gomito
roccioso. [...]
Boromir, giunto in quel momento, disse: "Abbiamo scavato un passaggio nel
cumulo di neve; di ciò dovranno esserci grati coloro che non possono correre
leggeri come gli Elfi." »
(SdA, libro II, cap. III)

Come si vede dal fotogramma, in effetti Legolas è l'unico a camminare sulla neve senza affondare in essa. E non è neppure l'unico elfo a manifestare quest'abilità. All'epoca dell'ottenebramento di Valinor e della ribellione di Fëanor, Fingolfin figlio di Finwë e di Indis, seppur riluttante, seguì il fratellastro in esilio nella Terra di Mezzo, assieme a gran parte del suo popolo, ma fu tradito da Fëanor il quale, dopo aver raggiunto le coste della Terra di Mezzo insieme ai suoi Elfi a bordo delle bianche navi dei Teleri, non tenne fede alla promessa di rimandarle indietro a prelevare il resto dei Noldor, e le diede alle fiamme. In tal modo Fingolfin fu costretto a seguire l'erta strada via terra che passava attraverso l'Helcaraxë, una striscia di ghiaccio stridente che collegava a Nord la terra di Aman e la Terra di Mezzo (a quel tempo la terra era piatta, come vedremo nella prossima lezione). Tale attraversamento era pericolosissimo e comportò numerose perdite, ma alla fine quegli antichi eroi riuscirono nell'impresa:
«
E Fingolfin, avvedutosi che Féanor l'aveva lasciato in Araman, a perire o a tornare pieno di vergogna in
Valinor, si sentì il cuore esulcerato; ma più che mai ora desiderava di pervenire, in un modo o nell'altro, alla
Terra di Mezzo e ritrovare Fëanor. Ed egli e la sua schiera vagarono a lungo nell'indigenza, ma il loro valore e la loro resistenza crebbero
con le durezze, poiché erano un forte popolo, i maggiori dei figli immortali di Eru Ilùvatar, ma ultimi a giungere
dal Reame Beato e non ancora esausti della stanchezza della Terra. Il fuoco dei loro cuori era ancora giovane e,
guidati da Fingolfin e dai suoi figli, nonché da Finrod e da Galadriel, osarono avventurarsi nel più crudo Nord; e,
non trovando altre risorse, alla fine affrontarono i terrori dello Helcaraxé e le crudeli colline di ghiaccio. Ben poche
delle gesta compiute in seguito dai Noldor sorpassarono in ardire e in durezza quel disperato passaggio. Quivi andò
perduta Elenwë, la moglie di Turgon, e molti altri del pari perirono; e fu con una schiera ridotta che Fingolfin mise
finalmente piede sulle Terre Esterne. »
(QS, cap. IX)
Dunque Fingolfin e i suoi bravi riuscirono a camminare su uno strato di ghiaccio talora piuttosto sottile, galleggiante sopra un gelido mare: talmente sottile che esso non sostenne il peso della povera Elenwë, ed ella sprofondò nelle acque tenebrose. Come spiegare scientificamente quest'abilità degli Elfi? I modi sono indubbiamente molteplici. Tanto per cominciare, gli Elfi potrebbero avere una corporatura particolarmente snella, priva degli antiestetici (e pericolosi per la salute) rotoli di grasso che caratterizzano noi Uomini. Ciò significa che il loro indice di massa corporea BMI, già utilizzato in quel che precede, avrebbe valori straordinariamente bassi. Con una massa corporea estremamente ridotta, anche il loro peso risulterebbe bassissimo, e permetterebbe agli Elfi di camminare tranquillamente sul ghiaccio e sulla neve, esercitando su di essi una pressione davvero esigua. Ci sono dei casi del genere, nella razza umana? Certamente sì. "L'uomo più magro del mondo" era il nome d'arte con cui fu conosciuto Harry V. Lewis, nato nel 1895 nello Iowa, che fino all'età di 12 anni era un ragazzo assolutamente normale; in seguito i medici gli diagnosticarono una forma giovanile di distrofia muscolare, che in breve lo portò a diventare un fragile scheletro vivente: era alto 171 cm ma pesava appena 36 kg. Il suo indice di massa corporea era perciò appena di 12, ai limiti della sopravvivenza! Per di più Harry seguiva una dieta strettissima a base di frutta, verdura, latte, piselli, fagioli e un uovo ogni tanto. Divenne famoso come l'"Uomo Ombra", esibendosi nel famoso Circo Barnum, restando in piedi su una piattaforma sotto gli occhi degli spettatori con indosso solo un paio di boxer, permettendo così a tutti di ammirare la sua estrema magrezza.


| A sinistra, una foto di Hary Lewis per gentile concessione della collezione di Milo Anthony e Cristina Boothe. A destra, Re Thingol in un disegno di Felix SotoMayor (da questo sito) |
Se gli Elfi avessero un indice di massa corporea simile a quello di Harry Lewis, indubbiamente per loro sarebbe facile camminare sulla neve senza sprofondarvi. Dopotutto, anche alcuni Elfi erano particolarmente longilinei: re Thingol Mantogrigio, che abbiamo già citato in quanto padre di Lúthien Tinúviel, era detto "il più alto di tutti i Figli di Ilúvatar": la sua esatta altezza non è specificata in alcuno scritto di Tolkien, ma si pensa che fosse alto non meno di due metri e mezzo. Per un confronto, l'essere umano più alto che si conosca era Robert Wadlow (1918-1940), detto "il Gigante dell'Illinois", che raggiunse i 2,72 metri di altezza: la sua taglia straordinaria e la sua continua crescita in età adulta erano dovuti a ipertrofia della ghiandola pituitaria, che si traduceva in un livello abnorme di ormone della crescita.
Non c'è dubbio che Wadlow, così come altri famosi colossi, come John Rogan (1868–1905), l'afroamericano più alto di sempre con i suoi 269 cm, potessero dare dei numeri al superbo Thingol, ma bisogna tenere conto di un fatto importante: Wadlow morì a 22 anni e Rogan a 37, poiché la loro smisurata statura comportava eccessivi problemi di salute. Thingol invece era considerato il più forte di tutti gli Eldar dopo Fëanor, e le prodezze che egli compì non erano certamente quelle di un essere debole e malaticcio. Wadlow inoltre al momento della sua morte pesava ben 220 Kg, quindi aveva un BMI pari a 220/(2,72)2 = 29,7. Se Thingol avesse avuto lo stesso BMI del Gigante dell'Illinois, avrebbe pesato non meno di 29,7 x (2,50)2 = 186 Kg: una massa certamente eccessiva per un Elfo in grado di camminare sulla neve senza sprofondare, o di camminare sul ghiaccio senza romperlo. Se invece avesse avuto il BMI di Harry Lewis, avrebbe avuto una massa di 12 x (2,50)2 = 75 Kg: più adatta ad un passo felpato sulla neve, ma decisamente troppo poco per diventare il secondo guerriero più forte della storia di Arda, qualità che richiedeva una massa muscolare non indifferente.
Dobbiamo però tenere conto di un altro fatto. La pressione non è solo direttamente proporzionale alla forza, ma anche inversamente proporzionale alla superficie. In altre parole, una forza anche ingente, se distribuita su una superficie molto ampia, affonda scarsamente. Tutto, allora, potrebbe risolversi in una questione di... piedi. Osserviamo infatti questo schizzo eseguito dallo stesso Tolkien, che rappresenta un Elfo:



| Dall'alto: un elfo in uno schizzo di Tolkien; lo sciatore di Rødøy in un francobollo norvegese; una ciaspola delle Dolomiti |
Come si vede, nella mente del Professore di Oxford gli Elfi avevano effettivamente una struttura estremamente longilinea, con arti molto sottili, ma soprattutto indossavano scarpe molto lunghe e dalla tipica forma a punta. E questa è sicuramente la calzatura più adatta per muoversi in sicurezza sulla neve: basti pensare alle racchette o agli sci, che sono indossati dai montanari proprio per ridurre la pressione sulla neve fresca, aumentando la superficie di contatto a parità di peso.
Tra l'altro, gli sci e le racchette da neve (o ciaspole) potevano essere conosciuti benissimo nella Terra di Mezzo, dato che secondo alcuni antropologi essi rappresentano il più antico mezzo di locomozione inventato dall'uomo, prima ancora della ruota. I ritrovamenti effettuati in Siberia e Lapponia datano i primi strumenti di questo tipo al 2500 a.C. circa; i più antichi sembrano quelli rinvenuti in una torbiera di Hoting, in Svezia, in ottimo stato di conservazione, mentre un'incisione rupestre sull'isola di Rødøy, in Norvegia, databile intorno al 2000 a.C. rappresenta una figura umana con ai piedi degli inconfondibili e lunghissimi sci: la si può vedere qui sopra, riprodotta su un francobollo norvegese, a confronto con l'elfo disegnato da Tolkien. Graffiti analoghi sono stati ritrovati anche in Siberia, Islanda, Italia (Val Camonica) e Canada. Nelle "Storie" di Erodoto si parla di popoli dell'Asia minore con "scarpe di legno" per spostarsi sulla neve: pochi dubbi che si trattasse di sci. Anche Senofonte e Strabone descrivono gli spostamenti delle popolazioni uralo-altaiche sulla neve mediante due assicelle assicurate ai piedi. Si pensa invece che le racchette da neve abbiano avuto origine nell'Asia centrale: Strabone descrive il loro uso da parte degli abitanti del Caucaso, e nell'arcaica scruttura cinese esisteva un ideogramma che indicava la "tavoletta per scivolare". Secondo l'archeologo britannico Jacqui Wood (1950-) anche Ötzi, la mummia del Similaun, aveva con sé un paio di ciaspole. Tuttavia esse vennero inventate indipendentemente anche dai nativi americani, dato che l'esploratore francese Samuel de Champlain (1574-1635) descrive il loro uso da parte dei Cree. Qui sopra si vede anche un modello tradizionale di ciaspola in legno (tale termine viene dal ladino "caspo", cioè "cesto", per la sua tipica intelaiatura).
Veri specialisti degli sci furono però gli scandinavi; la parola "sci" deriva probabilmente dall'antico norvegese "pezzo di legno tagliato". Una saga norvegese narra che nel Capodanno del 1206 nel quale due tra i più forti guerrieri di re Haakon III Sverresson, Torstein Skevla e Skjervald Skrukka, misero in salvo dai suoi nemici il figlio del re di soli due anni, attraversando le montagne di Dovre da Lillehammer a Østerdalen sotto una fitta tempesta di neve grazie all'uso di veloci sci di fondo; il bambino da loro salvato sarebbe divenuto Re Haakon IV Haakonsson (1202-1263), iniziatore della grandezza norvegese. In memoria dell'evento ogni anno si corre una famosa gara di fondo norvegese. la Birkebeinerlauf. Nel 1520 il Re di Svezia Gustavo I Vasa (1496-1560), convinto di aver perso la guerra contro i Danesi, stava fuggendo verso la Norvegia, quando venne raggiunto a Sälen da due suoi sudditi che avevano percorso senza mai fermarsi 89 chilometri sugli sci, per comunicargli che i suoi sudditi avevano ripreso in mano la situazione nel paese e volevano che Gustavo guidasse la rivolta. La prima descrizione scientifica degli sci la troviamo invece nella "Historia de Gentibus Septentrionalibus" scritta nel 1565 da Olao Magno (1490-1557), arcivescovo di Uppsala. Il primo italiano a usare un paio di sci pare sia stato l'esploratore ravennate Francesco Negri (1623-1698) nel suo viaggio in Lapponia nel 1663, durante il quale raggiunse Capo Nord: egli riferisce di « due tavolette sottili, che non eccedono in larghezza il piede, lunghe otto o nove palme, con la punta alquanto rilevata per non intaccar la neve ». Di fondamentale importanza per la nascita dello sci contemporaneo furono invece le innovazioni tecniche apportate dall'inventore ceco Mathias Zdarsky (1856-1940), che alla fine dell'Ottocento accorciò gli sci fino a un metro e 80 centimetri (all'inizio oltrepassavano i tre metri) e brevettò 25 tipi di attacchi. La prima vera gara sportiva sugli sci avvenne invece nel 1843 a Tromsø, in Norvegia (dove altrimenti?)
Escludendo che Legolas sia riuscito nell'impresa di correre così velocemente sulla neve utilizzando degli sci, è però verosimile che egli abbia fatto uso di un paio di calzature così grandi, da assomigliare in tutto e per tutto a delle ciaspole. Supponiamo ad esempio che Legolas fosse alto 1,80 m; attribuendogli il BMI di Robert Wadlow, egli avrebbe avuto una massa di 29,7 x (1,80)2 = 96,2 Kg;, cioè un peso di 96,2 x 9,8 = 943 N. Una normale racchetta da neve oggi in commercio ha una superficie di circa 600 cm2, per cui con indosso un paio di queste ciaspole il nostro Elfo Silvano avrebbe esercitato sulla neve una pressione di 943 N / 0,12 m2 = 7858 Pascal, valore che gli avrebbe tranquillamente consentito la sua performance sul Caradhras. Se poi il BMI del nostro Legolas fosse stato ancora più basso, l'impresa sarebbe risultata ancora più semplice, bastando calzature con una superficie plantare assai minore.
Ma non è tutto: esiste un'altra possibile spiegazione, per la corsa di Legolas sulla neve. Voglio infatti attirare la vostra attenzione su questo passaggio del brano letto sopra: « Scattò veloce come un corridore su terreno solido, ed avendo raggiunto rapidamente gli uomini che avanzavano a stento, li sorpassò, agitando la mano in segno di saluto, proseguì correndo lontano e scomparve dietro il gomito roccioso ». Osservate come il figlio di Re Thranduil non stia in equilibrio sulla neve, né si limiti a camminare sopra di essa, ma corra sul manto bianco ad alta velocità. In pratica, per spostarsi sulla neve compatta il nostro eroe ha l'accortezza di muoversi molto rapidamente. Durante una corsa, infatti, l'impronta di ogni piede è assai poco profonda, per via del rapidissimo contatto tra superficie plantare e strato nevoso: in pratica, il piede non fa in tempo ad affondare più di tanto. Si consideri ad esempio il ghepardo (Acinonyx jubatus), un felino diffuso in Africa australe che è conosciuto come il più veloce animale terrestre del pianeta Terra, come già detto nel capitolo precedente. Osservando al rallentatore riprese filmate della corsa del ghepardo sulla neve, si può verificare come le sue zampe raramente sprofondino più di un paio di centimetri, nonostante il peso del felino (circa 60 Kg) sia distribuito su zampe sottili e superfici plantari davvero esigue, che deporrebbero a favore di un'alta pressione e quindi di un deciso sprofondamento nella neve. Il ghepardo insomma sembra quasi "galleggiare" per effetto della sua corsa a rotta di collo, e non c'è motivo per negare che anche il furbo Legolas sfrutti questo fenomeno per far mangiare la polvere a tutti i suoi compari!

Veniamo ad un altro argomento dell'idrostatica desumibile dal Legendarium, e precisamente da "Lo Hobbit". A un certo punto della loro odissea, i Nani vengono catturati dagli Elfi Silvani e rinchiusi in celle separate, mentre Bilbo si sottrae all'arresto infilandosi l'Anello. A risolvere la situazione è il piccolo Hobbit, il quale si accorge che il Fiume Selva passa sotto la cantina, e che in essa saranno gettate le botti di vino vuote. Approfittando di una festa che distrae gli Elfi e del fatto che il capo delle guardie si è sbronzato, Bilbo libera Thorin e i suoi compagni e li fa nascondere all'interno delle botti. Queste vengono scaricate dagli Elfi nel fiume, e galleggiando in esse Bilbo e i quattordici Nani giungono a Pontelagolungo:
«
Presto la fortuna girò per il verso giusto: la corrente turbinosa trasportò
parecchi barili in uno stesso punto vicino a riva, e lì essi rimasero fermi
per un po', trattenuti da qualche radice nascosta. Allora Bilbo colse
l'occasione per arrampicarsi sopra il suo barile mentre veniva tenuto fermo
dagli altri. Strisciò su come un topo sul punto di affogare, e giacque
disteso in modo da distribuire il suo peso e mantenere l'equilibrio quanto
meglio poteva. La brezza era fredda ma sempre meno dell'acqua ed egli sperò
di non rotolare giùdi nuovo una volta ripartiti.
Non ci volle molto perchè i barili si liberassero di nuovo e girassero e
rigirassero giù per il fiume, e poi al centro della corrente. Allora trovò
abbastanza difficile tenersi in equilibrio, come aveva temuto; ma alla meno
peggio ci riuscì, anche se stava tremendamente scomodo. Per fortuna c'era
molta luce, e il barile era bello grosso e avendo varie crepe aveva ora
imbarcato una certa quantità di acqua. In tutti i modi era come cercare di
cavalcare, senza briglie e senza staffe, un puledro panciuto il cui unico
pensiero fosse quello di rotolarsi sull'erba. [...] Poi l'acqua turbinosa del
Fiume Selva travolse tutti quanti i tini e i barili e li spinse sulla riva
settentrionale, dove aveva scavato una vasta baia formata da una spiaggia
coperta di ciottoli sotto gli argini incombenti; sulla parte orientale essa
era protetta da un promontorio molto sporgente che formava un muro di roccia
dura. La maggior parte dei barili si arenò sul bordo della spiaggia.
»
(Lo
Hobbit, cap. IX)
I Nani nelle botti nella trilogia dedicata a "Lo Hobbit" da Peter Jackson
Ci troviamo di fronte al fenomeno del galleggiamento. Se le assi di legno di cui è fatta la botte venissero poste una per una sul pelo dell'acqua, è probabile che esse vadano a fondo come sassi. Perchè? Tutto merito del Principio di Archimede. Archimede di Siracusa (287-212 a.C.) era amico e forse anche parente del tiranno Gerone II, il quale un giorno gli mostrò una corona d'oro meravigliosamente cesellata, realizzata per suo conto da un orafo cui aveva consegnato una certa quantità d'oro. Gerone però sospettava che il gioielliere avesse fatto la cresta sull'oro, trattenendone per sé una parte e mescolando al resto del comune argento. La soluzione più semplice sarebbe stato fondere la corona, perchè in tal modo l'argento fuso sarebbe venuto a galla sull'oro fuso, ma Gerone non voleva saperne di distruggere il gioiello finemente lavorato. E allora, che fare? Scontentare un tiranno è sempre pericoloso. Mentre si arrovellava su come risolvere il problema, secondo quanto racconta lo scienziato romano Marco Vitruvio Pollione nel suo "De Architectura" (IX, 3), Archimede si immerse nella sua vasca per fare il bagno, e notò che entrando nell'acqua egli sentiva diminuire il suo peso. La scoperta lo rese così felice che uscì nudo di casa e corse per le strade di Siracusa esclamando "Eureka!" ("ho trovato!"). Archimede iniziò allora ad occuparsi di idrostatica e scrisse il trattato "Sui corpi galleggianti".
In tale trattato egli enunciò per la prima volta quello che oggi tutti conoscono come Principio di Archimede: un corpo immerso in un fluido riceve una spinta dal basso verso l'alto, chiamata Spinta Idrostatica o Spinta di Archimede, pari esattamente al peso del volume del fluido spostato, cioè al peso di una quantità di fluido il cui volume è pari a quello del corpo immerso. Il Principio ora enunciato è una conseguenza della Legge di Stevin da noi vista in precedenza. Si consideri infatti una delle botti scaricate dagli Elfi nel Fiume Selva, ed immaginiamo che essa si trovi completamente immersa in posizione eretta. Siano h l'altezza della botte, h1 la profondità della sua base superiore e h2 quella della sua base inferiore; naturalmente si ha h2 – h1 = h. Sia inoltre P1 la pressione sulla base superiore della botte, e P2 quella sulla base inferiore, come nello schema seguente:
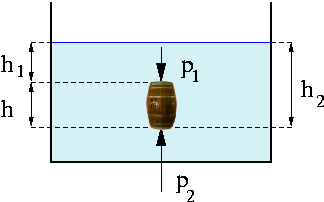
In base alla Legge di Stevin, avremo P1 = ρ g h1 e P2 = ρ g h2. Siccome h2 > h1, allora anche P2 > P1. Ciò significa che la botte sente una pressione maggiore sulla base inferiore che sulla base superiore, e quindi essa sarà spinta verso l'alto, esattamente come aveva osservato Archimede. Detta S l'area di ciascuna delle due basi della botte, la spinta idrostatica FA sarà pari a:
FA = F2 – F2 = P2 S – P2 S = ρ g ( h2 – h1 ) S = ρ g h S
Ma h S (area di base per l'altezza) rappresenta il volume V della botte, supponendo la sua forma poco lontana da quella cilindrica, per cui la precedente fornisce FA = ρ g V. Ora, la densità è pari alla massa divisa per il volume, quindi moltiplicando la densità per il volume si ottiene la massa. Tenendo conto che in questo calcolo ρ è la densità del fluido, non della botte, ne consegue che il prodotto ρ V rappresenta la massa m di un volume di acqua esattamente pari a quello della botte. E moltiplicando tale massa m per l'accelerazione di gravità g, troviamo il peso di un volume di acqua pari a quello della nostra botte. Abbiamo così dimostrato che la spinta archimedea è esattamente pari al peso del volume del fluido spostato!
In conseguenza di tale principio, un corpo immerso in un liquido o in un aeriforme subisce una diminuzione di peso, tanto maggiore quanto maggiore è la densità del fluido, dato che, come abbiamo testé visto, la Spinta di Archimede è direttamente proporzionale alla densità ρ di questo fluido (FA = ρ g V). Fu proprio questa sensazione di diminuzione di peso che, secondo Vitruvio, condusse Archimede alla scoperta del suo Principio; e fu sempre tale diminuzione di peso, che consentì allo scienziato siracusano di risolvere il problema della corona del tiranno Gerone. Infatti, Archimede prese la corona e la pesò in acqua, ottenendo ovviamente un peso minore di quello che essa aveva in aria. In seguito prese una quantità di oro zecchino il cui peso in aria è pari al peso in aria della corona, e la pesò in acqua. A sorpresa, trovò che in acqua essa pesava più della corona! Cosa poteva significare tutto questo? Evidentemente, che il gioielliere aveva barato. Infatti, se la corona di Gerone fosse stata d'oro puro, il suo peso in acqua sarebbe stato pari a quello dell'oro non lavorato. Se pesava meno, ciò voleva dire che aveva subito verso l'alto una spinta idrostatica maggiore, e quindi doveva avere un volume maggiore, il che implicava che doveva essere stata fabbricata mescolando all'oro dell'argento, che ha densità minore dell'oro (10.500 Kg/m3 contro 19.300 Kg/m3) e quindi, a parità di massa, occupa volume maggiore. Ovviamente l'unico scontento in tutta questa storia fu l'orafo, che perse la testa (letteralmente).
Nel caso dei Nani nelle botti, è il Principio di Archimede a spiegare perchè essi possono mettersi in salvo con questo espediente. Se infatti il peso P di un corpo immerso nel fluido supera la spinta di Archimede FA che esso riceve, esso fatalmente affonda. Se invece la spinta archimedea prevale sul peso, il corpo galleggia. Nel caso poi in cui peso e spinta di Archimede si equivalgono, il corpo fluttua nel fluido. Chiamando ρC la densità del corpo e ρF la densità del fluido, per avere FA > P occorre che:
ρF g V > ρC g V
e quindi che ρF > ρC. In pratica, il corpo galleggia se la sua densità è minore di quella del fluido. Una chiave inglese non galleggia certo sull'acqua (la densità dell'acciaio è di 7.800 Kg/m3, quella dell'acqua pura di 1.000 Kg/m3), ma galleggia sul mercurio, che ha una densità di ben 13.600 Kg/m3. Eppure, un nano ha una densità certamente maggiore di quella dell'acqua: la densità del corpo umano infatti oscilla tra i 1050 e i 1075 Kg/m3. Le cose peggiorano se aggiungiamo il peso del legno della botte e dei suoi cerchioni in ferro. E allora, come fanno le botti a galleggiare con il loro Nano dentro?
Evidentemente, il galleggiamento si ottiene quando il corpo in questione sposta un grande volume d'acqua. Per questo, ponendo sull'acqua un cubo di ferro avente massa di un chilogrammo, esso sicuramente affonda, dato che la sua densità è quasi otto volte superiore a quella dell'acqua. Le cose cambiano se con quel metallo costruiamo una struttura cava avente la forma dello scafo di una nave: essa pesa sempre un chilogrammo, ma per via della sua forma esso sposta una massa d'acqua molto maggiore di un chilogrammo, e così essa galleggia. Idem dicasi per le botti: visto il loro notevole volume, esse spostano una quantità d'acqua maggiore del loro peso, e dunque non vanno certo a fondo. Proviamo a fare due conti. Un Nano di media statura è alto un metro e mezzo, dunque possiamo supporre che questa fosse anche la profondità della botte. I Nani hanno una struttura fisica molto massiccia, per cui la botte deve essere bella larga: il diametro minore può essere pari a un metro, quello maggiore (a metà altezza) a un metro e venti. Per determinare il volume della botte useremo la formula approssimata messa a punto dal famoso astronomo e matematico Johannes Kepler (1571-1630) e pubblicata nel suo saggio "Nova stereometria doliorum vinariorum" del 1615:
![]()
dove r è il raggio di base ed R è il raggio a metà altezza. Sostituendo i dati sopra proposti, si ottiene:
![]()
Quindi la spinta di Archimede da essa avvertita quando è immersa nel Fiume Selva fino all'orlo è pari a:
![]()
La botte galleggia se il peso complessivo della botte stessa e del Nano al suo interno è inferiore a questa spinta. Ora dobbiamo stimare il peso della botte. Stimiamo la sua superficie laterale con quella di un barile di forma cilindrica, che ha come raggio il raggio minore della botte da noi considerata, cioè 60 centimetri. In tal caso l'area della superficie laterale vale:
![]()
Ora occorre stimare lo spessore s della botte. Fra lunghezza e spessore di ciascuna doga vi deve essere un giusto rapporto: per avere una botte solida è necessario che lo spessore della doga sia almeno il quattro per cento della sua lunghezza. Immaginando la botte cilindrica, ogni doga è lunga un metro e mezzo, e il 4 % di un metro e mezzo è pari a 6 centimetri. In realtà le doghe delle botti hanno uno spessore inferiore al centro rispetto alle estremità, ma per semplicità trascuriamo questa caratteristica. Allora il volume del legno del nostro barile sarà approssimativamente pari a:
![]()
A tale volume dobbiamo aggiungere quello della base inferiore, rappresentato da un cilindro di raggio pari a 60 cm e spesso 6 cm. Tale volume sarà pari a:
![]()
Sommando questi due volumi si ha un totale di 0,407 m3. Di solito una botte è realizzata in legno di quercia o di castagno; adottiamo per esso una densità di 800 Kg/m3 ed avremo una massa di 325,6 Kg, corrispondente a un peso di 3191 N circa (ricordiamo che si tratta di un limite superiore, essendo in realtà la nostra botte incurvata). Ricordiamo ora che un Nano in genere è alto un metro e mezzo e ha una struttura corporea molto massiccia. Riferendoci a Bombur, il più grasso tra i quattordici Nani della Compagnia, possiamo adottare un BMI estremo pari a 50. Allora la sua massa è pari a 50 x 1,502 = 112,5 Kg, che corrisponde a un peso di 1102,5 N. Sommandolo al peso della botte, avremo un peso totale di 3191 + 1102,5 = 4293,5 N, assai inferiore alla spinta archimedea massima sopra calcolata. Questo ci dice che, come si vede nel film, la botte non è immersa nel fiume fino all'orlo, ma emerge notevolmente dal pelo dell'acqua, abbastanza per impedirle di affondare imbarcando acqua a causa degli scossoni. Tenendo conto che FA = ρF g V, il volume della parte immersa in acqua della botte sarebbe pari a:
![]()
che corrisponde ad appena il 20 % del volume totale della botte sopra calcolato. Ovviamente il valore è sottostimato per via delle numerose approssimazioni (ad esempio, abbiamo trascurato i pesanti cerchioni in ferro della botte), ma dà l'idea di quanto sia intensa la spinta avvertita da un corpo che viene immerso in un fluido!

| Un curioso fotomontaggio in cui Thorin Scudodiquercia e i suoi Nani, così come appaiono nel ciclo di film tolkieniani diretti da Peter Jackson, appaiono lottare contro i Marziani de "La Guerra dei Mondi" di Herbert George Wells, come appaiono sulla copertina della storica rivista americana di fantascienza "Amazing Stories"! |

Prima di cambiare argomento, vale la pena di parlare di un'ultima grandezza fisica desumibile dal racconto di Tolkien e dalla trilogia di Peter Jackson, e relativa stavolta al moto dei fluidi, studiato dalla cosiddetta fluidodinamica. Nel fotogramma del film "Lo Hobbit - Un viaggio inaspettato" riportato qui sopra, infatti, si vedono le botti con i Nani roteare in un fiume vorticoso e pieno di schiuma, e questo ci suggerisce di aggiungere due parole circa il cosiddetto moto turbolento dei fluidi. Anche un'altra sezione del Legendarium ci induce a descrivere questo tipo di moto: dopo la loro partenza da Lórien, i membri superstiti della Compagnia dell'Anello discendono in barca le acque del grande fiume Anduin, giungendo alle rapide di Sarn Gebir, che li costringono a rallentare la loro marcia:
«
A Sam, seduto sulla barca di testa, fu assegnato il compito di sentinella.
[...] Mancava poco alla mezzanotte, e da qualche tempo si erano abbandonati
alla corrente, senza quasi adoperare le pagaie, quando all'improvviso Sam
lanciò un grido, A pochi metri di distanza delle forme cupe si ergevano dalle
acque, e alle sue orecchie giungeva il fragore di frutti vorticosi.
Una corrente rapida trascinava a sinistra, verso la riva orientale ove il
letto era sgombro. Mentre le loro barche venivano portate dai flutti in quella
direzione, i viaggiatori videro, a brevissima distanza, la pallida schiuma del
Fiume lambire delle rocce aguzze che giganteggiavano in mezzo al corso d'acqua
come una fila di denti. »
(SdA, libro II, cap. IX)
Qui leggiamo la parola chiave: flutti "vorticosi". Si dice che un fluido in un condotto o in un canale è animato da moto laminare quando tutte le molecole del fluido hanno velocità parallele fra di loro, e il fluido si può considerare composto da "lamine" di molecole che si muovono parallele l'una all'altra; si dice invece che è animato da moto turbolento quando l'attrito fra le diverse "lamine" di molecole ha il sopravvento, gli strati fluidi paralleli tra loro si rompono, e il moto provoca vortici e gorghi. Si provi ad aprire lentamente un rubinetto; all'inizio si avrà un singolo, sottile filo d'acqua, in cui tutte le molecole piovono verticalmente. Ma se si apre maggiormente il rubinetto, l'acqua fuoriesce gorgogliando, dando vita ad un moto turbinoso e irregolare. Cos'è che permette di marcare il passaggio dal primo regime di fluido al secondo?
Le equazioni che regolano
il moto del fluido, le cosiddette Equazioni di Navier-Stokes, formulate dal francese Claude-Louis Navier
(1785-1836) e dall'irlandese George Gabriel Stokes
(1819-1903), sono equazioni non lineari, e questo
rende pressoché impossibile fornire una loro soluzione "alle
quadrature", cioè una soluzione esatta per via analitica. Sono state
perciò proposte alcune leggi di tipo empirico, la più famosa delle quali
chiama in causa il Numero di Reynolds, così
detto dall'ingegnere
nordirlandese
Osborne Reynolds (1842-1912). Tanto per cominciare, Reynolds
suppose che la transizione tra moto laminare e moto turbolento dipendesse da
quattro fattori: la densità del fluido, la sua velocità,
la dimensione del condotto in cui fluisce e la
cosiddetta viscosità dinamica, che misura la
resistenza dei fluidi allo scorrimento. Indicata di solito con la lettera
greca μ, essa è definita come la forza che occorre applicare a
una "lamina" fluida per raggiungere la velocità della lamina posta a una distanza
unitaria da essa; le lamine fluide infatti si muovono a velocità diversa tra
di loro, e quelle vicine ai bordi del tubo sono più lente. La viscosità
dinamica μ può essere misurata come il coefficiente di
proporzionalità tra la forza scambiata tra le lamine (F) per
unità di superficie (S) e la variazione della velocità (vx)
lungo la sezione del fluido (come si vede in figura, x è
l'ascissa che misura il percorso del fluido nel condotto, e y
l'ordinata che misura la distanza dal centro del condotto):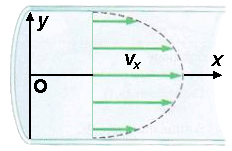
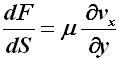
Da qui si deduce che la viscosità dinamica ha dimensioni fisiche:
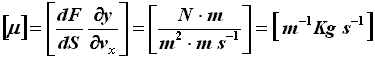
Nel sistema internazionale la viscosità dinamica si misura perciò in Pascal per secondo (Pa s), detti anche Poiseuille (Pl), in onore del medico francese Jean Léonard Marie Poiseuille (1799-1869), che studiò la viscosità del sangue nei capillari. Ovviamente una sostanza come il miele ha una viscosità assai più elevata di quella dell'acqua: 0,001 Pl è la viscosità dell'acqua a temperatura ambiente, mentre per il sangue umano μ = 0,003 Pl e per l'olio d'oliva μ = 0,08 Pl; la glicerina arriva a 1,5 Pl e l'olio lubrificante dei motori a 5 Pl. Quando la viscosità è pari a zero, si parla di superfluidità: l'elio liquido a 2,17 K diventa superfluido, tanto da arrampicarsi addirittura lungo le pareti della provetta che lo contiene! Un fluido con viscosità nulla e incomprimibile è detto fluido ideale. Si dicono invece fluidi newtoniani quelli la cui viscosità è indipendente dal rapporto dF/dS, cioè dalle forze scambiate tra le lamine fluide; la maggior parte dei fluidi reali è ovviamente non newtoniana. Il reciproco della viscosità è detto fluidità.
Vogliamo ora costruire un numero adimensionale utilizzando la densità ρ espressa in Kg m–3, la velocità v espressa in m s–1, la dimensione del condotto D espressa in m e la viscosità dinamica μ espressa in m–1 Kg s–1. Dovremo moltiplicarle dopo averle elevate ad opportuni esponenti, ed imporre che il risultato sia privo di dimensioni fisiche:
![]()
Sostituiamo le rispettive dimensioni fisiche:
![]()
e dopo semplici calcoli:
![]()
Dovremo perciò risolvere il sistema:
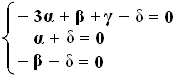
Risolvendolo si ottiene α = β = γ e δ = – α. Ponendo per semplicità α = 1, avremo β = γ = 1 e δ = – 1, per cui risulterà:
![]()
Questa grandezza adimensionale viene chiamata numero di Reynolds (in onore del già citato Osborne Reynolds), indicato con Re:
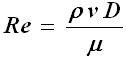
Viene definito numero di Reynolds critico il valore del numero di Reynolds in corrispondenza del quale si ha il passaggio da regime laminare a regime turbolento. Di solito si ritiene che, all'interno di un tubo cilindrico, per Re < 2500 si ha regime laminare, per Re > 2500 si ha regime turbolento, anche se non abbiamo a disposizione nessuna giustificazione teorica di questo asserto, puramente empirico. Ad esempio, la distanza tra due scogli del fiume Anduin in corrispondenza delle rapide di Sarn Gebir può misurare D = 5 metri, e l'acqua può percorrerle ad una velocità di un metro al secondo; conoscendo la densità ρ dell'acqua dolce, pari a 1000 Kg/m3, e la sua viscosità μ, pari come detto a 0,001 Pl, si ottiene Re = 5 x 106: un valore che sicuramente giustifica, in vicinanza di esse, un regime così turbolento da rendere difficoltosa la navigazione ai nostri eroi!
Ma ora andiamo oltre e passiamo ad un altro argomento, del quale potremo discutere a partire dai racconti del nostro Professore: la struttura del mondo e la gravitazione universale. Per inoltrarvi su questo nuovo territorio, cliccate qui e passiamo oltre!
![]()