![]()
|
...Onde si muovono a diversi porti (Par. I, 112-114) |
In questa pagina ci dedicheremo alle conoscenze di Meccanica che Dante ha inserito nel proprio poema. Com'è noto, la Meccanica è quella branca della Fisica che si occupa dello studio dei moti, e intorno all'anno 1300 il massimo autore che si era preoccupato di problemi connessi a tale studio era Aristotele di Stagira (384-322 a.C.). Pochi filosofi ebbero su un'intera epoca della storia un'influenza ampia e duratura come quella di Aristotele, e questo, più che all'impero bizantino, lo si deve agli Arabi come Averroè (vero nome Abu Walid Muhammad ibn Ahmad Muhammad ibn Rushd, 1126-1198), i quali tradussero le sue opere in arabo e le commentarono ampiamente. In Spagna, dove cultura araba e cultura latina si incontrarono, il corpus aristotelico e i commenti arabi furono tradotti in latino, e conobbero un successo immediato, tanto che senza l'influsso del pensiero aristotelico sarebbe stato impossibile il fiorire della Scolastica di Tommaso d'Aquino, che dominò il pensiero occidentale fino all'avvento della Rivoluzione Scientifica con Galileo e Newton. Naturalmente Dante Alighieri non può fare a meno di rendere omaggio al suo filosofo preferito, e lo fa ponendolo nel limbo insieme agli "spiriti magni" dell'antichità pagana, in posizione preminente rispetto a tutti gli altri:
« Poi ch'innalzai un poco più le ciglia,
vidi 'l maestro di color che sanno
seder tra filosofica famiglia.
Tutti lo miran, tutti onor li fanno » (Inf. IV, 130-133)
Tra l'altro a poca distanza da Aristotele c'è anche il suo commentatore Averroè:
« Averoìs, che 'l gran comento feo » (Inf. IV, 144)
Il fatto che Averroè, il massimo filosofo arabo di tutti i tempi, esercitò un'influenza enorme sulla cultura medioevale, è sottolineato dal fatto che Dante lo ricorda spesso anche nelle altre sue opere con l'aggettivo "Commentatore": si veda Convivio IV, XIII, 8; Monarchia I, III, 9; Quaestio V, 12 e XVIII, 46. Parlando di Fisica, gioverà aggiungere che probabilmente fu lui a introdurre il concetto di inerzia.

Raffaello, Aristotele
(particolare de "La Scuola di
Atene", Vaticano, Stanza della Segnatura, 1508-1511
Ma torniamo alla Fisica di Aristotele. Lo scopo di quest'ultima è quello di spiegare, non solo come il mondo risulti costituito, ma perché esso risulti costituito proprio così e non in altro modo; inoltre si tratta di una scienza qualitativa e non quantitativa, cioè non basata su formule matematiche, a differenza di quella di Galileo. Aristotele eredita da Empedocle la teoria di dei quattro elementi: terra, acqua, aria e fuoco, i quali, miscelati in proporzioni diverse, darebbero vita a tutta la realtà sensibile; per la teoria atomica in questo universo non c'è dunque posto. I quattro elementi tuttavia, anziché realtà fisiche come gli atomi di ossigeno e di idrogeno, sono intesi piuttosto come modi di essere. Anche i quattro esseri viventi dell'Apocalisse di Giovanni (4, 6-8) rappresentano probabilmente i quattro elementi aristotelici. Dante naturalmente assorbe immediatamente questo concetto, ad esempio nel discorso di Beatrice del VII Canto del Paradiso:
«
Tu dici: "Io veggio l'acqua, io veggio il foco,
l'aere e la terra e tutte lor misture
venire a corruzione, e durar poco..." » (Par. VII, 124-126)
Infatti questi elementi secondo Aristotele sono corruttibili, a differenza dell'etere di cui sono costituiti gli spazi circostanti il nostro mondo. Il filosofo di Stagira giustifica perché gli elementi siano proprio quattro sostenendo che la terra è l'elemento freddo e secco, e per sua spontanea natura tende verso il basso; essa deve essere controbilanciata dal suo elemento contrario, il fuoco, che è caldo e secco, e tende spontaneamente verso l'alto. Fra essi devono esistere altri due elementi con funzioni mediatrici: l'acqua, fredda e umida, e l'aria, calda e umida. Per terra ed acqua il moto naturale è verticale verso il basso, per aria e fuoco è verticale verso l'alto; in tal modo Aristotele spiega la caduta dei gravi senza bisogno di far ricorso ad alcuna teoria di gravitazione universale e ad alcuna azione a distanza. Dante possiede il concetto di centro di gravità del pianeta Terra, perchè così lo definisce nel terzultimo canto dell'Inferno:
«
E mentre ch'andavamo inver' lo mezzo
al quale ogne gravezza si rauna » (Inf. XXXII, 73-74)
e così invece nell'ultimo:
«
quand'io mi volsi, tu passasti 'l punto
al qual si traggon d'ogne parte i pesi. » (Inf. XXXIV, 110-111)
Ma esso non è il centro di un campo di forze, bensì solo il punto geometrico verso il quale si dirige il moto naturale di due dei quattro elementi corruttibili che costituiscono tutto il mondo sublunare. Per gli altri due il luogo naturale sono le sfere celesti: il vapore, ad esempio, tende ad allontanarsi dal centro della Terra dirigendosi verso lo spazio e verso la Luna, per via del prevalere del fuoco nel miscuglio di acqua e fuoco che lo compone. L'acqua calda ancora allo stato liquido invece non contiene abbastanza fuoco per essere portata verso l'alto, e quindi tende a ricadere verso il centro della Terra. Ne consegue che il mondo secondo "il maestro di color che sanno" ha una struttura a quattro sfere concentriche: una più interna costituita di terra, una di acqua, una d'aria e una di fuoco. Tuttavia, parlando della "Questio de aqua et terra" abbiamo già visto che queste sfere non vanno intese come gli strati concentrici (crosta, mantello, nucleo esterno, nucleo interno) che secondo la moderna geologia costituiscono l'interno della Terra, essendo i quattro elementi mescolati in vario modo fra di loro, bensì come "luoghi naturali", ossia strati geometrici verso cui ognuno di essi tende spontaneamente a portarsi, non appena libero di muoversi.
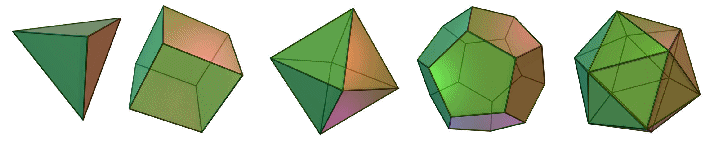
Da questa teoria dei "luoghi naturali" Aristotele ricava anche l'unicità del mondo, in netto contrasto con le ipotesi di Anassagora e Democrito: secondo lui, infatti, ogni porzione di terra, di acqua, di aria, di fuoco tende naturalmente alla sua sfera, e perciò nel globo sublunare devono essersi concentrate tutta la terra, l'acqua, l'aria e il fuoco a disposizione dell'universo; non avanza quindi alcun residuo di tali elementi per formare altri mondi. Niente UFO, quindi, nell'universo dantesco. I corpi celesti sono invece formati da etere (dal greco "ardente"), un quinto elemento eterno, immutabile, impalpabile, senza peso, perfettamente elastico e perfettamente trasparente. C'è da dire che l'idea dei "quattro più uno" elementi è preesistente, e risale invece al "Timeo", uno dei più famosi dialoghi di Platone, in cui quest'ultimo ha un'idea arditissima, suggeritagli dalla geometria euclidea. Platone sapeva che possono esistere solo cinque poliedri regolari (detti ancor oggi "platonici"), i quali hanno tutti gli spigoli, tutte le facce e tutti gli angoli solidi uguali tra di loro. Essi sono il tetraedro (le facce sono quattro triangoli equilateri), il cubo o esaedro (le facce sono sei quadrati), l'ottaedro (le facce sono otto triangoli equilateri), il dodecaedro (le facce sono dodici pentagoni regolari) e l'icosaedro (le facce sono venti triangoli equilateri). Riflettendo sul perchè seguendo i postulati di Euclide non possono esistere più di cinque poliedri regolari, Platone ebbe l'idea di associarli agli elementi costitutivi dell'universo! La terra sarebbe legata allo stabile cubo, il fuoco (che si insinua dovunque) al puntuto tetraedro, l'aria alla "mobile" forma dell'ottaedro e l'acqua al multisfaccettato icosaedro. Dopotutto questa visione non è lontanissima dalla cristallografia moderna, in cui gli atomi che formano i cristalli si distribuiscono lungo strutture estremamente regolari. Ma così restava fuori un poliedro, il dodecaedro; Platone ebbe allora l'idea geniale di associarlo a un quinto elemento, l'etere appunto, perchè, essendo formato da pentagoni regolari, esso è collegato a uno dei numeri più importanti della storia, il rapporto aureo o "divina proporzione", la cui ideazione era riportata a Dio stesso; perciò il dodecaedro aveva sicuramente origine divina, e non poteva, per usare le parole stesse di Platone, che essere « la forma usata dalla Divinità per ricamare le costellazioni sulla volta dei cieli ». E così nacque quella che possiamo chiamare "la prima Teoria Unificata della storia della scienza", la quale spiega, seppure in modo ingenuo, perchè gli elementi sono cinque, non uno di più, non uno di meno. Il grande pittore spagnolo Salvador Dalì (1904-1989), dopo la sua conversione al cattolicesimo, dipinse nel 1955 il celeberrimo "Sacramento dell'Ultima Cena", in cui l'Eucaristia è istituita dentro ad un dodecaedro regolare, dentro al quale appare anche l'immagine di Cristo già risorto. Questo perchè il Santissimo Sacramento è di origine divina, eterna e immutabile, così come la Risurrezione di Nostro Signore, e la sua norma non può che essere il solido regolare a dodici facce tanto caro a Platone!

Salvador Dalì, "Il Sacramento dell'Ultima Cena", Washington, National Gallery
Proprio per l'eternità e l'immutabilità dell'etere, il cosmo rappresenta per Aristotele una realtà immutabile, in contrapposizione alla Terra, mutevole e corruttibile. Per questo secondo il nostro filosofo esistono in realtà due scienze fisiche: una riguarda il mondo sublunare, e come si è visto è caratterizzata da moti verticali; l'altra vale solo nello spazio esterno, ed è dominata dal moto circolare uniforme, perchè tale sarebbe il moto naturale della quintessenza. Infatti, parlando della cosmologia dantesca, vedremo che i moti dei corpi celesti sono tutti rappresentabili come una composizione di moti circolari uniformi. Nel suo "Sidereus Nuncius" (1610), Galileo Galilei annuncerà appunto la scoperta che la Luna possiede montagne come la Terra e che il Sole è punteggiato di macchie, e dunque essi non sono affatto sfere perfette di etere, ma sono composti della stessa materia di cui è fatta la Terra. In seguito Isaac Newton con la teoria della gravitazione, detta appunto "universale", baserà tutta la filosofia naturale sul concetto che non vi sono due fisiche ma una sola, valida in ogni angolo dell'universo.
Ignaro di ciò, Dante accetta per vere le teorie aristoteliche, e Beatrice le espone in modo chiarissimo al principio dell'ascesa di Dante verso l'Empireo:
« E cominciò: "Le cose tutte quante
hanno ordine tra loro, e questo è forma
che l'universo a Dio fa simigliante.
Qui veggion l'alte creature l'orma
de l'etterno valore, il qual è fine
al quale è fatta la toccata norma.
Ne l'ordine ch'io dico sono accline
tutte nature, per diverse sorti,
più al principio loro e men vicine;
onde si muovono a diversi porti
per lo gran mar de l'essere, e ciascuna
con istinto a lei dato che la porti.
Questi ne porta il foco inver' la luna;
questi ne' cor mortali è permotore;
questi la terra in sé stringe e aduna" » (Par. I, 103-117)
Vediamo di riassumere il discorso di Beatrice. Tutte le creature sono ordinate fra di loro, in modo da costituire un tutto armonico, e questo ordine rappresenta la "forma", cioè il principio essenziale che rende l'universo simile a Dio. Come diceva infatti Tommaso d'Aquino:
«
Quaecumque autem sunt a Deo, ordinem habent ad invicem et ad ipsum Deum »
[Tutte le cose infatti che procedono da Dio, sono ordinate fra di loro e
rispetto a Dio] (Summa Theologica I, XLVII, 3)
Come si vede, lo sguardo di Dante coglie ogni cosa nello splendore e nell'ordine del suo essere, e per questo è simbolo di quell'Infinito che l'uomo continuamente ricerca. In questo ordine le creature dotate di un intelletto superiore (le "alte creature") riconoscono il segno della potenza e della sapienza del Creatore, il quale è il fine ultimo a cui tende "la toccata norma" dell'universo. Tutte le specie naturali ("nature") sono allora inclinate ("accline") in modo diverso ("per diverse sorti"), secondo le condizioni loro assegnate, essendo esse più o meno vicine al loro comune Principio, che è Dio; e così, nella brulicante e sconfinata vita dell'universo ("lo gran mar de l'essere"), tutte si muovono in differenti direzioni ("porti"), stimolata ciascuna dal suo particolare istinto. Anche qui si sente l'eco di un passo di San Tommaso:
« Cum
omnia procedant ex Voluntate divina, omnia suo modo per appetitum inclinantur
in bonum, sed diversimode »
[Poiché tutte le cose procedono dalla Volontà di Dio, tutte a loro modo sono
inclinate a desiderare il bene, ma in maniere diverse] (Summa Theologica I,
LIX, 1)
Questo ordine istintivo è quello che porta il fuoco a salire naturalmente verso la sua sfera, cioè in direzione del Cielo della Luna; questo ordine muove e regola ("è permotore") le funzioni vitali negli esseri privi di ragione ("i cor mortali"); questo ordine, infine, esplicandosi come forza di gravità, tiene unita e compatta la Terra. Veramente a volte la materia può andare in direzione contraria alla sua naturale inclinazione, ma si tratta di una mostruosità, di un traviamento, di un'evidente violazione delle leggi naturali. Infatti poco dopo il Sommo Vate aggiunge:
«
Vero è che, come forma non s'accorda
molte fiate a l'intenzion de l'arte,
perch'a risponder la materia è sorda,
così da questo corso si diparte
talor la creatura, c'ha podere
di piegar, così pinta, in altra parte;
e sì come veder si può cadere
foco di nube, sì l'impeto primo
l'atterra torto da falso piacere. » (Par. I, 127-135)
In altre parole: come accade che all'intenzione dell'artista non sempre corrisponda la forma dell'opera da lui realizzata, per colpa della materia che non è disposta a tradurla in atto, allo stesso modo talvolta la creatura si allontana dall'inclinazione naturale ("da questo corso"), che è libera, per quanto indirizzata istintivamente al bene ("così pinta", cioè così spinta), di fuorviarsi e di volgersi al male. Come talvolta il fuoco, che tenderebbe naturalmente a salire, cade invece sulla Terra sotto forma di fulmine, così la primitiva inclinazione, che porterebbe l'uomo a salire verso il Cielo, lo rivolge invece verso la Terra ("l'atterra"), traviata da una falsa immagine di bene. Si noti che Dante crede erroneamente che il fulmine sia fatto di fuoco vivo, mentre Benjamin Franklin (1708-1790) riconoscerà in esso un fenomeno di natura elettrica, ed oggi sappiamo che esso è composto di plasma, riscaldato da una potente scarica da milioni di Volt dovuta all'elettricità statica delle nubi. Come si vede, l'Alighieri si sforza di tradurre la sua esperienza mistica (l'ascesa al Paradiso dall'Eden in cima alla Montagna del Purgatorio) in termini di rigorosa razionalità aristotelica.
Da notare che, poiché Aristotele poneva al centro della sua teoria il mezzo, egli non poteva accettare il concetto di vuoto, centrale invece nella teoria atomistica di Democrito di Abdera (460-370 a.C.): essendo uno spazio vuoto privo di qualsiasi sostanza, e potendo il moto, secondo Aristotele, verificarsi solo attraverso un mezzo, l'assenza di sostanza era un'idea inconcepibile. Le teorie atomistiche di Democrito vengono decisamente contrastate dallo stesso Dante, poiché il filosofo di Abdera rifiutava il concetto di "moto naturale" e di "luoghi naturali", e quindi in ultima analisi, come visto, di Provvidenza divina che tutto finalizza al bene ultimo delle cose. Per Democrito il moto degli atomi è assolutamente casuale, per caso essi si aggregano e altrettanto per caso essi si disgregano; ed infatti, incontrandolo nel Limbo subito dopo Aristotele, Socrate e Platone, l'Alighieri così lo ha apostrofato:
« Democrito che 'l mondo a caso pone » (Inf. IV, 136)
(degli atomi e dei modelli atomici riparleremo in una delle prossime lezioni)

Lucifero nell'edizione della commedia di Alessandro Vellutello (1534)
C'è un altro particolare da aggiungere. Com'è ben noto, dopo la spaventosa visione di Lucifero dalle tre teste, Virgilio annuncia che « è da partir, ché tutto avem veduto » (Inf. XXXIV, 69), ed invita Dante ad avvinghiarsi al suo collo; quindi, quando le ali sono aperte in posizione favorevole, con un salto il poeta mantovano si appiglia al busto peloso del demonio, e inizia a scendere di vello in vello. Arrivato al punto dove le cosce si attaccano alle anche, Virgilio compie un'operazione che a prima vista Dante non comprende: si gira nella direzione in cui Lucifero ha le zanche (le gambe) e ricomincia a salire:
«
lo duca, con fatica e con angoscia,
volse la testa ov'elli avea le zanche,
e aggrappossi al pel com'om che sale,
sì che 'n inferno i' credea tornar anche.
"Attienti ben, ché per cotali scale",
disse 'l maestro, ansando com'uom lasso,
"conviensi dipartir da tanto male." » (Inf. XXXIV 78-84)
In tal modo, i due poeti sorpassano il centro della terra ed entrano nell'emisfero australe, cosicché la gravità è inversa, e Virgilio deve risalire. Colpisce quel « con fatica e con angoscia », e lo sapete perchè? All'epoca dell'Alighieri si era convinti che, man mano ci si avvicina al centro della Terra, la gravità andasse aumentando, e dunque Virgilio avrebbe dovuto compiere uno sforzo sovrumano per voltarsi e poi per risalire. Apparentemente la Gravitazione Universale di Newton afferma la stessa cosa, sostenendo che la forza di gravità è inversamente proporzionale al quadrato della distanza, e quindi, dimezzando la distanza fra due masse, la loro forza di attrazione quadruplica. Ma ciò vale tra due masse puntiformi! Quando ci si trova al centro della Terra, si è circondati in ogni direzione da masse equivalenti di roccia, disposte con simmetria sferica, e quindi, se una di queste masse ci attira in una direzione, la massa ad essa simmetrica ci attira con la stessa forza in direzione contraria. Conclusione: la gravità al centro della Terra è nulla, e Virgilio non dovrebbe fare alcuna fatica a girarsi, né tantomeno ansimare mentre avvisa il suo discepolo che quella è l'unica scala con cui abbandonare la voragine infernale. Chi ne era ben consapevole era il commentatore lucchese Alessandro Vellutello, il quale infatti, nella sua edizione della Divina Commedia datata 1534, ha rappresentato (come si vede sopra) un Lucifero che se ne sta... "sospeso a mezz'aria" tra la "ghiaccia" infernale e le rocce al confine tra i due emisferi. Il significato simbolico è chiaro: rocce e ghiaccio hanno ribrezzo di Lucifero, e si rifiutano di toccarlo. Ma altrettanto chiara è la spiegazione che ci fornisce la Fisica: Lucifero sta sospeso perchè su di esso non agisce alcuna forza gravitazionale. La fatica di Virgilio, chiara allegoria della pena con cui l'uomo abbandona una condizione di peccato per convertirsi e rimettersi sulla diritta via, andrà dunque spiegata in altro modo, magari perchè il pelame del demonio è unto, scivoloso ed offre tutt'altro che un appiglio agevole...
![]()
Venendo in modo più specifico alle leggi del moto enunciate da Aristotele, com'è noto egli stabilisce una famosa proporzionalità diretta tra la forza cui un corpo è soggetto e la velocità che esso assume. Di conseguenza, il moto è impossibile in assenza di forze. Ma questa conclusione appare in contrasto con l'esperienza quotidiana: ad esempio, in che modo una freccia può continuare ad avanzare attraverso l'aria, anche dopo essersi staccata dalla corda tesa che le ha dato l'avvio? Un problema non da poco, e certamente a conoscenza di Dante, se questi fa più volte ricorso nelle sue similitudini proprio al moto di una freccia attraverso "l'aere", ad esempio in questi due passi:
«
Corda non pinse mai da sé saetta
che sì corresse via per l'aere snella... » (Inf. VIII, 13-14)
« E sì come saetta che nel segno
percuote pria che sia la corda queta,
così corremmo nel secondo regno. » (Par. V, 91-93)
Per rispondere a queste obiezioni, Aristotele avanzò l'ipotesi secondo cui una freccia in movimento creerebbe una sorta di vuoto dietro di sé, che la spingerebbe avanti, in accordo con la sua interpretazione del moto, che prevede l'interazione tra l'oggetto in movimento e la causa (forza) che glielo trasmette. A parte il fatto che all'epoca questa teoria era difficile da confermare o smentire separatamente, un altro punto debole della teoria era rappresentato dal fatto che, se ciò fosse stato vero, allora un oggetto che si sposta nel vuoto dovrebbe viaggia a velocità infinita. Ma il nostro Filosofo liquidava l'obiezione, come visto sopra, con la teoria dell'horror vacui, secondo cui il concetto stesso di vuoto è impossibile.
Galileo risponderà a questa teoria nel suo magistrale "Discorsi e dimostrazioni matematiche intorno a due nuove scienze" (1638), ricorrendo a quello che in tedesco è chiamato Gedankenexperiment, cioè "esperimento pensato": un esperimento che non si può realizzare nella pratica, per via dell'impossibilità di eliminare gli attriti, ma che risulta estremamente istruttivo. Si immagini dunque di avere un piano inclinato e una biglia che rotola giù lungo di esso. Se davanti a questo piano inclinato se ne pone un altro, e se si riesce a trascurare ogni tipo di attrito, si osserva che, qualunque sia la pendenza del secondo piano, la biglia risalirà sempre alla stessa quota da cui è partito (nel linguaggio della Fisica moderna, ciò è una conseguenza del principio di conservazione dell'energia meccanica nei campi irrotazionali). Allora, se davanti al primo piano inclinato se ne pone uno orizzontale, la biglia cercherà inutilmente di raggiungere la quota di partenza, procedendo perciò all'infinito, senza bisogno di essere spinta da alcuna forza. Il moto di questa biglia viene chiamato moto inerziale.

Galileo ne ricava il cosiddetto Primo Principio della Dinamica: « Un corpo persiste nel suo stato di moto rettilineo uniforme o di quiete, finché una causa esterna (cioè una forza) non viene a turbare questo stato. »
Come sappiamo, non solo su questo punto la Fisica di Aristotele era in errore. Infatti egli era convinto che la forza applicata ad un corpo risulti proporzionale alla velocità da esso acquistata (il che in termini moderni equivale a dire che l'equazione del moto è di primo e non di secondo ordine), e quindi, in assenza di forze, il corpo avrebbe dovuto necessariamente restare fermo, come detto sopra. Nella sua monumentale opera "Philosophiae Naturalis Principia Mathematica" (1687) sir Isaac Newton dimostrò invece che la forza è proporzionale all'accelerazione secondo la famosa equazione (Secondo Principio della Dinamica):
F = m a
e quindi l'applicazione di una forza a un corpo in moto rettilineo uniforme ne provoca l'accelerazione o la decelerazione, a seconda la forza sia equiversa o controversa al moto (m è la massa inerziale del corpo; per una dimostrazione sperimentale, vedi ad esempio qui) Quello che è considerato uno dei più clamorosi "errori" della fisica pregalileiana è però facilmente spiegabile alla luce della mancata considerazione dell'ineliminabile presenza delle forze d'attrito. Infatti facendo rotolare una biglia giù da un piano inclinato e facendola correre su un piano orizzontale si può osservare che presto o tardi essa si ferma, ma ciò è dovuto all'attrito con l'aria e con la superficie piana, non certo per l'assenza di una forza propulsiva. Inoltre, per quanto riguarda il Secondo Principio, Aristotele e i suoi seguaci, a parte le stelle, avevano la possibilità di osservare solo ciò che accade sulla Terra, cioè nell'aria. Ora, a basse velocità la forza d'attrito viscoso che si oppone al moto è all'incirca proporzionale in modulo alla velocità e di verso opposto a quello del moto. In queste condizioni perciò l'equazione di Newton va così riscritta:
F – η v = m a
dove η è la costante di attrito viscoso, che dipende dall'aria e dalla forma del corpo, e v il modulo della velocità. All'epoca imporre forti accelerazioni era difficile, e le velocità che si raggiungevano erano dovute ad accelerazioni piccole e prolungate nel tempo. In questa situazione, dopo il momento della partenza del corpo da fermo, era quasi sempre vero che alle velocità a cui si muovevano i corpi valesse la disuguaglianza η v >> m a. Dopo la partenza quindi il termine inerziale m a si poteva quasi sempre trascurare rispetto ai termini cinetici che contengono v. Si ottiene quindi:
F = η v
Ed ecco spiegata la meccanica di primo ordine tanto cara agli aristotelici, in cui la forza serve a muovere il corpo, non ad accelerarlo. Essi dunque non erano poi tanto in errore, eccezion fatta meno evidentemente per i pianeti: infatti fu proprio riflettendo sui moti planetari, che Newton ricavò i tre Principi della Dinamica.
Come curiosità ulteriore relativa al tempo di Dante, è interessante capire la traiettoria di un proiettile di cannone di allora. All'atto pratico, questa non è affatto una parabola, bensì somiglia ad un triangolo con la punta un po' arrotondata. Il proiettile quindi all'inizio si muove quasi in linea retta (gli aristotelici avrebbero detto fino a che dura l'impulso che lo ha lanciato), e poi, arrivato all'apice, cade in modo quasi verticale (gli aristotelici avrebbero detto che torna al suo luogo naturale).
Questo fatto è dovuto alla rapida dipendenza dalla densità dell'aria e quindi dalla temperatura del coefficiente viscoso dell'aria (in prima approssimazione si tratta di una dipendenza esponenziale). Quando il proiettile esce dalla canna è arroventato, rarefa l'aria attorno a sé e la resistenza viscosa risulta molto piccola. la traiettoria è quindi una parabola, la cui prima parte però si approssima bene con una retta, poiché il vertice è posto molto in alto. Durante il suo moto, il proiettile si raffredda fino ad arrivare alla temperatura che corrisponde al gomito della dipendenza esponenziale della viscosità. Qui il coefficiente viscoso diviene bruscamente molto grande, e poiché la velocità del proiettile è alta (circa settanta metri per secondo, 250 km/h), la viscosità dipende dalla velocità al quadrato. Il proiettile quindi rallenta bruscamente, arriva in frazioni di secondo alla velocità limite in aria e cade quasi in verticale. Alla fine non siamo molto lontani da un triangolo! (*).

L'autore di questo sito verifica in laboratorio le leggi del moto rettilineo uniforme con la collaborazione di una sua studentessa
![]()
Questo per quanto riguarda il moto rettilineo. Se però passiamo ad analizzare il moto curvilineo, le grandezze scalari (cioè rappresentate da un numero dotato di segno) non sono più sufficienti. Infatti, se affermo che in un piano mi sono spostato di 10 cm, devo specificare: in che direzione? E seguendo quale verso? Per questo sono state introdotte nuove grandezze, definite vettori (dal latino "veho", "trasporto"). Si dice vettore una grandezza fisica caratterizzata da un punto di applicazione (il punto di partenza), un modulo (la lunghezza del vettore, nel nostro caso di quanto mi sono spostato), una direzione (la retta su cui giace il vettore, cioè la direzione che seguo spostandomi) e un verso (il senso di percorrenza lungo quella retta). Il vettore viene perciò rappresentato come un segmento orientato, cioè mediante una freccia il cui verso è indicato dalla punta del vettore stesso. Sono grandezze scalari lo spostamento (non però la lunghezza di un percorso), la velocità, l'accelerazione, la forza, il momento di una forza, la quantità di moto, il momento angolare, la pressione; il lavoro, l'energia, il calore, la corrente elettrica, il tempo sono invece grandezze scalari.
Il concetto di vettore doveva essere ben chiaro nella mente di Dante, almeno a livello embrionale, se egli, per indicare ciò che ha una direzione e un verso oltre ad una lunghezza, usa in tutte e tre le Cantiche proprio la metafora della freccia!
« Corda non pinse mai da sé saetta
che sì corresse via per l'aere snella,
com' io vidi una nave piccioletta
venir per l'acqua verso noi in quella... » (Inf. VIII, 13-16)
« Forse in tre voli tanto spazio prese
disfrenata saetta, quanto eramo
rimossi, quando Bëatrice scese. » (Purg. XXXII, 34-36)
«
E sì come saetta che nel segno
percuote pria che sia la corda queta,
così corremmo nel secondo regno. » (Par. V, 91-93)
Nel primo caso si tratta della barca di Flegias che attraversa la Palude Stigia proprio in direzione di Dante e Virgilio; nel secondo caso di quanto si era mossa la Processione Simbolica nel Giardino dell'Eden; nel terzo caso di Beatrice e Dante che salgono nel Secondo Cielo, quello di Mercurio. Nel secondo caso, oltre al verso e alla direzione, si accenna anche al modulo del vettore: tre tiri d'arco! E non è tutto. Così Dante dice al proprio avo Cacciaguida nel Canto XVII del Paradiso:
« per che la voglia mia saria contenta
d'intender qual fortuna mi s'appressa:
ché saetta previsa vien più lenta » (Par. XVII, 25-27)
Al di là dell'evidente significato simbolico della terzina (è meglio conoscere in anticipo i mali che stanno per piombarci addosso), qui vi è un accenno alla capacità di prevedere la traiettoria della freccia e più in generale del proiettile; di questo si occupa quella parte della meccanica chiamata balistica. Ancora nel Rinascimento il matematico francescano Luca Pacioli (1445-1517) nel suo "Quesiti e inventioni diverse" (1554), in cui si occupa anche di balistica, sostiene che la traiettoria di un proiettile sparato da un archibugio è un arco di circonferenza. Invece bastano pochi semplici calcoli per rendersi conto che non è così.
Sia un punto materiale sparato orizzontalmente con velocità v0 dal bordo di un tavolo. Esso è soggetto solo alla forza di gravità, diretta verso il basso, per cui ungo la direzione orizzontale non sente alcuna accelerazione, e il suo moto è rettilineo uniforme. Invece verticalmente sente l'accelerazione di gravità g e nessuna componente della velocità iniziale. Ne seguono queste equazioni del moto (la y è stata considerata positiva verso il basso):
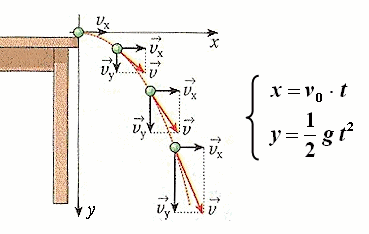
Ricavando la t dalla prima equazione e sostituendola nella seconda si ottiene:
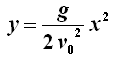
che è chiaramente l'equazione di una parabola con il vertice nel punto di lancio. Conclusione: il moto della freccia è parabolico, non circolare, e può essere previsto utilizzando le equazioni del moto di Galilei e di Newton! Anche il salto in lungo di un'atleta del resto è un esempio di moto parabolico, come dimostra molto bene questo mosaico di fotografie:

E non è finita: in altri passi danteschi infatti si parla anche del moto circolare uniforme! È questo il caso, per esempio, del penultimo canto di tutta la Divina Commedia:
« Sì come rota ch'igualmente è mossa » (Par. XXXIII, 144)
Per spiegare ai suoi lettori che il suo animo, dopo la visione divina, è perfettamente in pace con l'universo, il nostro Poeta ricorre alla metafora della ruota che è fatta girare "ugualmente", cioè in modo tale che in ogni secondo l'angolo di cui essa ruota è lo stesso; in altre parole, la velocità angolare della ruota è costante, ed essa si muove proprio di moto uniforme!
Da un altro passo del Paradiso è poi facile ricavare una delle caratteristiche precipue di questo tipo di moto:
« E come cerchi in tempra d'orïoli
si giran sì, che 'l primo a chi pon mente
quïeto pare, e l'ultimo che voli;
così quelle carole, differente-
mente danzando, de la sua ricchezza
mi facieno stimar, veloci e lente. » (Par. XXIV, 13-18)
Dante si trova nel Cielo delle Stelle Fisse, e vede gli spiriti beati radunarsi in cerchi concentrici che girano vorticosamente su se stessi. E qui si innestano le conoscenze scientifiche del Pellegrino dell'Oltretomba: come le ruote ("cerchi") del meccanismo di un orologio girano a differenti velocità, tanto che le prime (le più interne) sembrano quasi ferme, e le ultime (le più esterne) paiono quasi volare, così quelle corone danzanti ("carole") di anime, con il differente ritmo del loro girare, danno la misura della loro diversa ricchezza di grazia, cioè del maggiore o minore grado della loro beatitudine. Così commenta in proposito Manfredi Porena:
« Negli orologi antichi, il moderatore del movimento si comunicava dal motore dell'orologio (peso o molla) per mezzo di successive ruote dentate, moltiplicando sempre più la velocità. Tanto più, in confronto di questa velocità, la prima ruota, mossa direttamente dal motore, pareva ferma, perchè essa faceva un giro in dodici ore. »
Evidente è il significato dell'osservazione scientifica di Dante: considerando una ruota in moto circolare uniforme, qualsiasi sia la loro distanza dal centro, tutti i punti sono animati dalla medesima velocità angolare ω, mentre i punti più esterni hanno velocità lineare v assai maggiore di quelli più vicini al mozzo, stante la proporzionalità diretta tra velocità angolare (in rosso nella figura sottostante) e raggio (in giallo):
![]()

E, allo stesso modo, una ruota calettata sullo stesso asse di un'altra di diametro doppio avrà la stessa velocità angolare, ma la periferia della seconda ruota si muoverà con velocità lineare doppia di quella della prima. Per inciso, si noti quella curiosa rima di "mente" con "differente-", prima parte di "differentemente": l'avverbio spezzato tra i due versi (con termine tecnico enjambement) sembra riprodurre verbalmente la differenza di velocità tra i cerchi concentrici dei beati, e tra le ruote dentate dell'orologio!
Allo stesso fenomeno si riferisce anche un verso del Purgatorio:
«
Li occhi miei ghiotti andavan pur al cielo,
pur là dove le stelle son più tarde,
sì come rota più presso a lo stelo. » (Purg. VIII, 85-87)
Il concetto è lo stesso: gli occhi "ghiotti" (cioè avidi di conoscenza) del poeta sono attirati dal Polo Antartico, là dove le stelle ruotano più lentamente, così come in una ruota si muovono più lentamente i suoi punti più vicini all'asse di rotazione ("lo stelo"). All'occhio curioso di Dante non è sfuggita la differente velocità delle stelle lontane o vicine all'asse terrestre, un argomento di cui riparleremo a proposito della Geografia Astronomica! Evidentemente Galilei aveva proprio ragione, quando scriveva:
« L'intelletto umano intende alcune cose così perfettamente, e ne ha così assoluta certezza, quanto se n'abbia l'istessa natura: e tali sono le scienze matematiche pure, cioè la geometria e l'aritmetica: delle quali l'intelletto divino ne sa bene infinite proposizioni di più, perché le sa tutte: ma di quelle poche intese dall'intelletto umano credo che la cognizione agguagli la divina nella certezza obiettiva... » ("Dialogo sopra i due massimi sistemi del mondo")
Ma la Meccanica di Dante non si ferma qui. Chi l'avrebbe mai detto, che nel "Sacrato Poema" è possibile rintracciare anche riferimenti alla Relatività? Per scoprirlo assieme a me, cliccate qui e andate avanti.
(*) Grazie all'amico Eugenio Iannone per questi suggerimenti.