Se non che al viso e di sotto mi venta

Che ci crediate o noi, qui parleremo di Relatività. Prendiamo infatti in considerazione tre passi del Paradiso. Il primo viene dal Canto ottavo:

« Io non m'accorsi del salire in ella;
ma d'esservi entro mi fé assai fede
la donna mia ch'i' vidi far più bella. » (Par. VIII, 13-15)

Dante sta salendo dal Cielo di Mercurio a quello di Venere (« la bella Ciprigna » di Par. VIII, 2, essendo Venere nata a Cipro), ma la cosa curiosa è che Dante non si accorge di essere salito di quota. Se ne rende conto solo osservando la sua donna, perchè la bellezza e lo splendore di Beatrice crescono mano a mano che ella sale verso l'Empireo. E la cosa comincia già ad apparirci strana. La stessa cosa si verifica due canti più innanzi, quando il Poeta sale dal Cielo di Venere a quello del Sole:

« ...ma del salire
non m'accors'io, se non com'uom s'accorge,
anzi 'l primo pensier, del suo venire. » (Par. X, 34-36)

Secondo i commentatori, il "primo pensiero" è quello che si forma all'improvviso, non preparato da una precedente successione d'idee, e del quale prendiamo coscienza solo quando ce lo troviamo nella mente. In altre parole, Dante Alighieri si accorge improvvisamente di essere salito di un Cielo, senza preavviso, come se pensasse ancora di trovarsi intorno a Venere, e di colpo si accorgesse che il Sole era lì a un tiro di schioppo. Sempre più strano! E analogamente avviene al momento della salita al Cielo di Marte:

« Quindi ripreser li occhi miei virtute
a rilevarsi; e vidimi translato
sol con mia donna in più alta salute.
Ben m'accors'io ch'io era più levato,
per l'affocato riso de la stella,
che mi parea più roggio che l'usato. » (Par. XIV, 82-87)

La vista di Beatrice ha abbagliato il nostro autore, ma ora i suoi occhi riacquistano la capacità visiva e tornano a volgersi verso l'alto; Dante si ritrova così "traslato" (termine curiosamente caratteristico della moderna Matematica!) "in più alta salute", cioè ad un grado più alto di beatitudine. Anche stavolta Dante si è accorto di essere asceso verso l'Empireo solo perché il fulgore del Sole è stato sostituito dal rosseggiare di Marte ("roggio" è un toscanismo). A questo punto occorre cercare una risposta: come fa il Ghibellin Fuggiasco a non accorgersi che sta ascendendo, tanto da restare sorpreso quando si ritrova vicino ad un nuovo corpo celeste? C'è una sola possibile spiegazione: Dante sta salendo di moto rettilineo uniforme, cioè di moto inerziale.

Del moto inerziale si è già parlato nel capitolo precedente, ma qui ci interessa un particolare aspetto di esso, messo in luce per la prima volta da Galileo Galilei nel suo capolavoro, il "Dialogo sui Due Massimi Sistemi del Mondo" (1632). Esso rappresenta non solo una grande opera scientifica ma una vera pietra militare della letteratura italiana (potete leggerne il testo integrale a questo link), essendo strutturato come un dialogo tra tre personaggi: Salviati che rappresenta il punto di vista di Galileo, Simplicio che incarna l'aristotelico di stampo medioevale, e Sagredo che fa da moderatore del dibattito. Naturalmemte Simplicio, che - come afferma ironicamente il suo nome - fa la figura del sempliciotto, difende il sistema geocentrico con i soliti argomenti, praticamente dei luoghi comuni della Fisica aristotelica, tra i quali il più banale riguarda il fatto che, se la Terra fosse in movimento, noi saremmo sbalzati nello spazio in quattro e quattr'otto. Così afferma infatti il portavoce di Aristotele:

« Conferma finalmente l'istesso coll'argomento preso dall'esperienza de' gravi, li quali, cadendo da alto a baso, vengono a perpendicolo sopra la superficie della Terra; e medesimamente i proietti tirati a perpendicolo in alto, a perpendicolo per le medesime linee ritornano a basso, quanto bene fussero stati tirati in immensa altezza: argomenti necessariamente concludenti, il moto loro esser al centro della Terra, che senza punto muoversi gli aspetta e riceve. »

L'argomento è semplice e tratto dall'esperienza: i gravi cadono a perpendicolo, non obliquamente come accadrebbe se la Terra ruotasse attorno all'asse. Per controbattere al proprio avversario, Salviati (alias Galileo) enuncia allora quello che oggi è noto come Principio di Relatività Galileiana, e che afferma l'impossibilità di distinguere il moto rettilineo uniforme dalla quiete. Lasciamo la parola allo scienziato pisano:

« E qui, per ultimo sigillo della nullità di tutte le esperienze addotte, mi par tempo e luogo di mostrar il modo di sperimentarle tutte facilissimamente. Riserratevi con qualche amico nella maggiore stanza che sia sotto coverta di alcun gran navilio, e quivi fate d'aver mosche, farfalle e simili animaletti volanti; siavi anco un gran vaso d'acqua, e dentrovi de' pescetti; sospendasi anco in alto qualche secchiello, che a goccia a goccia vadia versando dell'acqua in un altro vaso di angusta bocca, che sia posto a basso: e stando ferma la nave, osservate diligentemente come quelli animaletti volanti con pari velocità vanno verso tutte le parti della stanza; i pesci si vedranno andar notando indifferentemente per tutti i versi; le stille cadenti entreranno tutte nel vaso sottoposto; e voi, gettando all'amico alcuna cosa, non piú gagliardamente la dovrete gettare verso quella parte che verso questa, quando le lontananze sieno eguali; e saltando voi, come si dice, a piè giunti, eguali spazii passerete verso tutte le parti. Osservate che avrete diligentemente tutte queste cose, benché niun dubbio ci sia che mentre il vassello sta fermo non debbano succeder cosí, fate muover la nave con quanta si voglia velocità; ché (pur che il moto sia uniforme e non fluttuante in qua e in là) voi non riconoscerete una minima mutazione in tutti li nominati effetti, né da alcuno di quelli potrete comprender se la nave cammina o pure sta ferma: voi saltando passerete nel tavolato i medesimi spazii che prima né, perché la nave si muova velocissimamente, farete maggior salti verso la poppa che verso la prua, benché, nel tempo che voi state in aria, il tavolato sottopostovi scorra verso la parte contraria al vostro salto; e gettando alcuna cosa al compagno, non con più forza bisognerà tirarla, per arrivarlo, se egli sarà verso la prua e voi verso poppa, che se voi fuste situati per l'opposito; le gocciole cadranno come prima nel vaso inferiore, senza caderne pur una verso poppa, benché, mentre la gocciola è per aria, la nave scorra molti palmi; i pesci nella lor acqua non con piú fatica noteranno verso la precedente che verso la sussequente parte del vaso, ma con pari agevolezza verranno al cibo posto su qualsivoglia luogo dell'orlo del vaso; e finalmente le farfalle e le mosche continueranno i lor voli indifferentemente verso tutte le parti, né mai accaderà che si riduchino verso la parete che riguarda la poppa, quasi che fussero stracche in tener dietro al veloce corso della nave, dalla quale per lungo tempo, trattenendosi per aria, saranno state separate; e se abbruciando alcuna lagrima d'incenso si farà un poco di fumo, vedrassi ascender in alto ed a guisa di nugoletta trattenervisi, e indifferentemente muoversi non piú verso questa che quella parte. E di tutta questa corrispondenza d'effetti ne è cagione l'esser il moto della nave comune a tutte le cose contenute in essa ed all'aria ancora, che per ciò dissi io che si stesse sotto coverta; ché quando si stesse di sopra e nell'aria aperta e non seguace del corso della nave, differenze piú e men notabili si vedrebbero in alcuni de gli effetti nominati: e non è dubbio che il fumo resterebbe in dietro, quanto l'aria stessa; le mosche parimente e le farfalle, impedite dall'aria, non potrebber seguir il moto della nave, quando da essa per spazio assai notabile si separassero; ma trattenendovisi vicine, perché la nave stessa, come di fabbrica anfrattuosa, porta seco parte dell'aria sua prossima, senza intoppo o fatica seguirebbon la nave, e per simil cagione veggiamo tal volta, nel correr la posta, le mosche importune e i tafani seguir i cavalli, volandogli ora in questa ed ora in quella parte del corpo; ma nelle gocciole cadenti pochissima sarebbe la differenza, e ne i salti e ne i proietti gravi, del tutto impercettibile. »

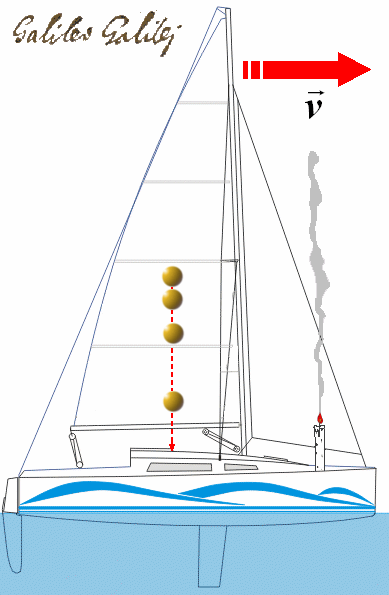
L'argomentazione stupisce tanto è semplice. Secondo Simplicio, se si lascia cadere una biglia da un punto di una nave ferma, essa dovrebbe muoversi lungo la verticale, mentre, se la nave è in moto, esso dovrebbe restare indietro tanto più quanto più velocemente la nave si muove. Se la nave si muove di moto rettilineo uniforme, dimostra invece Salviati, ciò è manifestamente errato. La biglia segue la stessa traiettoria con moto uniformemente accelerato, e con accelerazione g = 9,8 m/s², sia che l'esperimento venga eseguito su di una nave ferma nel porto, sia che esso sia ripetuto mentre la nave è in moto rettilineo uniforme. Di conseguenza l'osservatore solidale con la barca non è in grado di distinguere, usando soli esperimenti di cinematica, se la nave sia ferma o se si muova di velocità costante in modulo, direzione e verso.

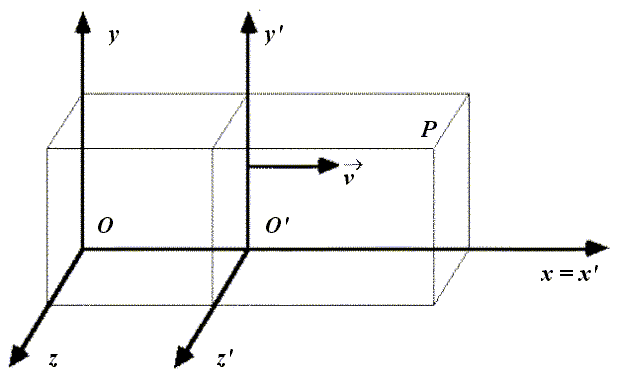
Ripetiamo l'esperimento concettuale di Galileo in termini moderni. Immaginiamo due osservatori, uno fermo sul molo e uno a bordo della barca. Potremo rappresentare questi due osservatori mediante due sistemi di riferimento, che indicheremo con Oxyz e con O'x'y'z'. Il secondo si muove rispetto al primo con velocità v. Le posizioni di un punto P viste dall'uno e dall'altro osservatore sono allora legate dalla relazione:

x = x' + OO' = x' + v t'

Dividendo entrambi i membri per t (poiché Galileo assume che i tempi misurati dai due osservatori siano gli stessi), si ricava:

V = V' + v'

dove V è la velocità rilevata dal sistema di riferimento Oxyz, e V' quella rilevata da O'x'y'z'. Quelle che abbiamo scritte si dicono Trasformazioni Galileiane (valgono in un sistema in moto rettilineo uniforme rispetto all'altro lungo l'asse x, ma sarebbe possibile generalizzarle a qualunque tipo di moto).

Scriviamo ora la legge di trasformazione delle velocità in due istanti di tempo distinti:

in t₁:   V₁ = V₁' + v'

in t₂:   V₂ = V₂' + v'

naturalmente v è la stessa per entrambi i sistemi, essendo il moto relativo rettilineo uniforme. Sottraendo membro a membro le due equazioni si ha:

V₁ – V₁' = V₂ – V₂'

cioè:

ΔV₁ = ΔV₂

Dividendo ora ambi i membri per Δt, si ha:

ΔV₁ / Δ t = ΔV₂ / Δ t

ossia a₁ = a₂ , essendo l'accelerazione media data dalla variazione di velocità nell'unità di tempo. In altre parole, un punto materiale è animato dalla stessa accelerazione rispetto a due osservatori in moto rettilineo uniforme l'uno rispetto all'altro.

Ciò è fondamentale ai fini del nostro ragionamento. Se infatti entrambi gli osservatori da noi considerati misurano una stessa forza con un dinamometro (ad es. il peso di due oggetti identici), entrambi otterranno lo stesso valore, perchè la forza è proporzionale all'accelerazione, e le accelerazioni misurate dai due osservatori sono identiche. Generalizzando, ne consegue che la forza agente su di un corpo è invariante, quando si passa da un sistema di riferimento all'altro in moto rettilineo uniforme rispetto ad esso. Se dunque l'uomo sulla barca lascia cadere una biglia, ne descriverà il moto nello stesso identico modo dell'uomo sul molo. E così anche il fumo della candela salirà in verticale sia che essa sia posta sul molo, sia che essa sia posta sulla barca a vela (trascurando ovviamente le eventuali correnti d'aria), e lo stesso dicasi per le mosche e le farfalle che volano dentro la cambusa, e per le gocce che cadono dentro la bocca del vaso.

In conseguenza di tutti questi ragionamenti, Galileo Galilei poté enunciare quello che oggi è noto come Principio di Relatività Galileiana (o di Relatività Classica). Se chiamiamo sistemi inerziali quelli in quiete o in moto rettilineo uniforme l'uno rispetto all'altro, esso afferma che:

« In tutti i sistemi inerziali valgono le stesse leggi del moto »

Ed ecco spiegato allora perchè Dante non si accorge della propria ascesa di Cielo in Cielo: sta ascendendo di moto rettilineo uniforme, e dunque per lui valgono le stesse leggi del moto (cioè i Tre Principi della Dinamica) che valevano quando era in quiete. Certamente per spostarsi egli dovrà prima accelerare e poi decelerare, ed allora il suo sistema non sarà più inerziale; ma, se l'accelerazione è abbastanza bassa, il nostro Poeta non si accorge degli "scossoni", tanto più che è sicuramente distratto dalla vicinanza della bellissima Beatrice. Anche noi, se ci troviamo a bordo di una carrozza ferroviaria, ci accorgiamo che parte se ci sentiamo leggermente schiacciati contro il sedile, e che rallenta o si arresta se ci sentiamo spinti in avanti, ma finché il treno si muove di moto uniforme, ci comporteremo esattamente come se fosse ancora fermo in stazione, tanto da giungere talora ad affermare: "Toh! Siamo già partiti? Non me ne sono neppure accorto..."

E questo non è il solo riferimento del poema ai moti relativi. Infatti, dopo aver visitato il Settimo Girone dell'Inferno, quello dei violenti, Dante si trova nella situazione di dover scendere nell'Ottavo Girone, costituito dalle già citate Malebolge. Ma un'alta « ripa discoscesa » (Inf. XVI, 103), impossibile da scalare, separa i due cerchi dell'Inferno. Che fare? Virgilio lascia cadere nel burrone la corda che aveva legata intorno alla vita, probabilmente il simbolo della temperanza (ricorda il cordone dei francescani) che si oppone ad ogni maleficio infernale; e poco dopo i due poeti vedono arrivare, quasi nuotando nell'aria, « una figura... / maravigliosa ad ogne cor sicuro » (Inf. XVI, 132), che si rivela essere il custode di Malebolge, Gerione. Questi è una delle tante figure della mitologia greca che Dante trasforma genialmente in demoni dell'Inferno cristiano, ma mentre gli antichi poeti lo descrivono come un gigante dai tre corpi ("tergeminus Geryon" secondo Virgilio, Eneide VIII, 202; "ter amplum Geryonem" secondo Orazio, Odi, II, XIV, 7-8; "prodigium triplex... in tribus unum" secondo Ovidio, Eroidi IV, 91-92), Dante ce lo descrive invece come un drago medievale creato giustapponendo le parti di tre diverse creature, un mostro con viso umano, zampe di leone e corpo maculato da serpente:

« E quella sozza imagine di froda
sen venne, e arrivò la testa e 'l busto,
ma 'n su la riva non trasse la coda.
La faccia sua era faccia d'uom giusto,
tanto benigna avea di fuor la pelle,
e d'un serpente tutto l'altro fusto;
due branche avea pilose insin l'ascelle;
lo dosso e 'l petto e ambedue le coste
dipinti avea di nodi e di rotelle. » (Inf. XVII, 7-15)

Si tratta di una evidente incarnazione della frode, visto che con il volto di uomo giusto inganna le sue vittime, per poi ghermirle con le zampe di leone e finirle con la coda, armata di un uncino da scorpione. I "nodi" e le "rotelle" di cui è dipinto il suo corpo rappresentano quasi certamente gli intrighi e i raggiri di cui si servono i frodatori per ottenere i loro scopi. Virgilio convince il bizzarro essere a portare sé e Dante sui « suoi omeri forti » (Inf. XVII, 42) onde superare il burrone. Ovviamente il Ghibellin Fuggiasco è tutt'altro che entusiasta a quella prospettiva, ma per non fare brutta figura con il suo Maestro e suo Autore sale su quelle che per lui sono soltanto delle « spallacce » (Inf. XVII, 91), e Virgilio lo abbraccia per essere sicuro che non cada. L'Anima Gentile Mantoana apostrofa così il drago infernale:

« Gerïon, moviti omai:
le rote larghe, e lo scender sia poco;
pensa la nova soma che tu hai! » (Inf. XVII, 97-99)

Evidentemente Virgilio conosce molto bene la Fisica! Infatti, perchè chiede a Gerione di scendere a spirale (com'è evidentemente sua abitudine) con "rote larghe", cioè compiendo giri molto ampi, e scendendo di poco ad ogni giro, cioè molto lentamente?

La risposta è facile. Il moto di Gerione si compone di un moto rettilineo uniforme verso il basso e di un moto circolare uniforme in un piano orizzontale (in pratica il centro di rotazione si muove di moto rettilineo uniforme verso il basso). La composizione dei due moti genera una traiettoria la cui forma è chiamata elica cilindrica.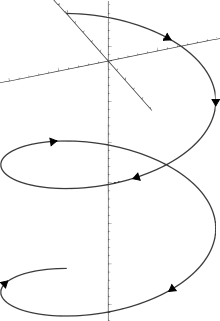 Le sue equazioni parametriche sono:

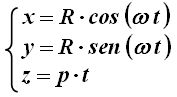
dove R è il raggio dell'elica e p è il suo passo, cioè di quanto l'elica scende (o sale) in un giro completo. Se p > 0, l'elica è destrogira; se p < 0, è levogira (si parla di "chiralità" dell'elica). La proiezione di questa curva tridimensionale su un piano perpendicolare all'asse è una circonferenza, e il moto proiettato su questo piano appare circolare uniforme. Ora, si sa che l'accelerazione centripeta nel moto circolare uniforme è data da:

essendo ω la velocità angolare; più piccola è quest'ultima, minore è l'accelerazione, e più il moto apparirà inerziale, quindi senza scossoni, pericolose inclinazioni, eccetera. Conclusione: se Gerione "nuota" nell'aria con ampie spirali, il viaggio di Dante sarà più confortevole: lo attesta la Fisica!

Ma non è solo per questo, che abbiamo tirato in ballo il signor Gerione. Infatti Dante Alighieri, uno dei primi uomini (almeno nella sua finzione poetica) a sperimentare il volo planato, è anche uno dei primi a sperimentare il terrore di finire spiaccicato al suolo, tanto da rievocare alla sua mente i falliti tentativi di Fetonte, che non seppe guidare il carro di suo padre il Sole, e di Icaro, che si avvicinò troppo all'astro solare e senti sciogliersi la cera che gli faceva aderire le ali al corpo:

« Maggior paura non credo che fosse
quando Fetonte abbandonò li freni,
per che 'l ciel, come pare ancor, si cosse;
né quando Icaro misero le reni
sentì spennar per la scaldata cera,
gridando il padre a lui "Mala via tieni!",
che fu la mia, quando vidi ch'i' era
ne l'aere d'ogne parte, e vidi spenta
ogne veduta fuor che de la fera. » (Inf. XVII, 106-114)

In pratica, Dante sa che Gerione si è staccato dalla solida roccia, che attorno a lui non c'è che aria, eppure a causa del buio non riesce a distinguere un bel niente, neppure l'effettivo moto della fiera. Una situazione del genere, aggravata dalla totale deprivazione sensoriale, causerebbe il panico in chiunque di noi. Eppure il nostro eroe sa che si sta muovendo. Perché? Perchè, come egli stesso osserva:

« Ella sen va notando lenta lenta;
rota e discende, ma non me n'accorgo
se non che al viso e di sotto mi venta. » (Inf. XVII, 115-117)

Dal momento che, secondo l'invito di Virgilio, Gerione si muove con lentezza in larghe giravolte, non sono percepibili gli effetti dovuti alla non inerzialtà del sistema di riferimento solidale con il demonio, tuttavia Dante intuisce che si sta muovendo perchè sente il movimento in direzione opposta dell'aria. In pratica, per un osservatore solidale con il burrone infernale, l'aria è ferma e Dante sta scendendo attraverso di essa lungo un'elica cilindrica. Invece, per un osservatore solidale con il poeta, è Gerione ad essere fermo, e di conseguenza è l'aria che si muove verso di esso; la velocità dell'aria è addirittura scomposta da Dante nella sua componente orizzontale ("al viso") e verticale ("di sotto"), l'una dovuta al contributo del moto circolare uniforme in un piano orizzontale, l'altra all'effetto del moto rettilineo uniforme verso il basso.

Né questo è l'unico passo dell'Inferno in cui troviamo descritto in modo accurato il fenomeno dei moti relativi: spostiamoci infatti nel Canto XXXI, quello dei Giganti cui abbiamo già dedicato una pagina di questo ipertesto. Anche in questo caso, Dante e Virgilio si trovano nella necessità di superare un burrone, quello che separa l'ottavo dal nono cerchio, dove stanno i traditori. In questo caso non c'è un Gerione disponibile, ma Virgilio ha un colpo di fortuna: vede il gigante Anteo, che non è incatenato, a differenza degli altri, non avendo preso parte alla Guerra di Flegra che i Titani scatenarono contro gli Dèi dell'Olimpo. Subito l'autore dell'Eneide lo adula per convincerlo a depositare lui e Dante sul letto ghiacciato del Cocito. Inopinatamente il gigante obbedisce, afferra Dante e Virgilio e li mette giù, senza fare neppure una parola, del resto come tutti gli altri giganti escluso Nembrotte, il cui urlo è indecifrabile, come vedremo nella lezione successiva. Quando Dante vede Anteo chinarsi verso di lui, si sente assalire dal terrore, come già fatto del resto quando ha visto i Giganti nella penombra per la prima volta:

« Così forando l'aura grossa e scura,
più e più appressando ver' la sponda,
fuggiemi errore e crescémi paura » (Inf. XXXI, 37-39)

e quando Efialte ha cercato di divincolarsi dalle catene per afferrarlo:

« Non fu tremoto già tanto rubesto,
che scotesse una torre così forte,
come Fïalte a scuotersi fu presto.
Allor temett'io più che mai la morte,
e non v'era mestier più che la dotta,
s'io non avessi viste le ritorte. » (Inf. XXXI, 106-111)

cioè sarebbe bastata la paura (la "dotta", un toscanismo) a farlo morire, se non ci fossero state le catene a rassicurarlo. Da notare anche il tema della torre, che ritorna continuamente per dare ai lettori l'idea di qualcosa di molto alto ma di relativamente innocuo. Ecco infatti come il nostro poeta descrive Anteo che si china verso di lui:

« Qual pare a riguardar la Carisenda
sotto 'l chinato, quando un nuvol vada
sovr'essa sì, ched ella incontro penda:
tal parve Antëo a me che stava a bada
di vederlo chinare, e fu tal ora
ch'i' avrei voluto ir per altra strada. (Inf. XXXI, 136-141)

La Garisenda è la minore delle due torri bolognesi, superstiti della celebre Bologna turrita del Medioevo: costruita fra il 1109 ed il 1119 dalla potente famiglia omonima, oggi è alta 48 metri ed ha uno strapiombo di 3,2 m, ma inizialmente era alta oltre 60 m e fu ribassata nel XIV secolo a causa di un cedimento del terreno, che la rese obliqua e pericolante. A chi la guarda dal basso, e precisamente dalla parte dove essa pende ("sotto 'l chinato"), quando una nuvola le viene incontro, per via di una comune illusione ottica sembra che la nuvola resti ferma e sia la torre ad inclinarsi verso l'osservatore. In pratica, l'occhio umano diventa automaticamente solidale con la nuvola, e questo per vari motivi, primo dei quali perchè la nuvola è enorme e posta molto in alto, e il cervello inconsciamente ci fa credere che più un oggetto è grosso e lontano, più lentamente esso si deve muovere. Ma allora, se il nostro occhio diventa solidale con il sistema di riferimento della nuvola, per via delle Trasformazioni di Galileo è la torre a muoversi rispetto ad esso. L'effetto risultante è alquanto spaventoso, come sottolinea il nostro poeta, che in quel momento avrebbe voluto percorrere ogni via fuorché quella, per lasciare le Malebolge!

E non è tutto: al principio dell'ultimo Canto dell'Inferno, così Virgilio si rivolge al suo accolito:

« "Vexilla regis prodeunt inferni
verso di noi; però dinanzi mira",
disse 'l maestro mio, "se tu 'l discerni". » (Inf. XXXIV, 1-3)

"Si avvicinano i vessilli del re dell'Inferno", vuole dire Virgilio con la sua citazione latina, la quale non fa altro che storpiare l'inizio di un inno di Venanzio Fortunato, vescovo di Poitiers nel VI secolo, entrato a far parte della liturgia cattolica del Venerdì Santo. In quel caso i "Vexilla regis" stanno a indicare la Croce, ma in questo passo esse rappresentano le sei ali del gigantesco Lucifero. Che ci crediate o no, anche in questo verso ci sono tracce di Relatività. Infatti Dante e Virgilio vedono i vessilli di Satana che si avvicinano, ma in realtà questa descrizione è fatta nel loro sistema di riferimento: nel sistema di riferimento dell'Inferno, ovviamente, le ali di Belzebù sono ferme, e sono i due poeti ad avanzare verso di esse! Questa sottigliezza relativistica non impedirà però al poeta, anche in questo caso, di sentirsi né morto né vivo dalla paura!

Prima di chiudere questo argomento, facciamo un cenno a una Relatività ben più complessa di quella Classica di Galileo, della quale si trova traccia nella "Divina Commedia". Per trovare i brani incriminati, però, ci dovremo spostare dall'Inferno alle altre cantiche. Tanto per cominciare, un cenno all'annoso problema della velocità della luce. Ecco la similitudine in cui si fa riferimento a questo fenomeno fisico:

« E come in vetro, in ambra o in cristallo
raggio resplende sì, che dal venire
a l'esser tutto non è intervallo,
così 'l triforme effetto del suo sire
ne l'esser suo raggiò insieme tutto
sanza distinzïone in essordire. »  » (Par. XXIX, 25-27)

A parlare è Beatrice, la quale sta parlando della Creazione, durante la quale il Signore trasse simultaneamente dal nulla la forma (le intelligenze angeliche), la materia (il mondo ancora informe) e infine il composto indissolubile di materia e forma, cioè i Cieli. Così interpreta il Sapegno:

« Questo triplice ("triforme") effetto dell'atto creativo raggiò nella pienezza del suoe essere dall'idea di Dio ("il suo sire"), tutto insieme, senza processo di tempo, come un raggio luminoso che ferisce un corpo trasparente o traslucido ("in vetro, in ambra o in cristallo"), istantaneamente, senza alcun intervallo di tempo, lo compenetra tutto della sua luce. »

In altri termini, l'effetto della Creazione fu istantaneo allo stesso modo in cui è istantanea la propagazione della luce. Questo fatto, che oggi sappiamo bene essere erroneo, era considerato vero fin dalla più remota antichità, e dopo Dante lo sarebbe stato considerato fino al Seicento. Così si esprimeva ad esempio San Tommaso d'Aquino in un passo che il nostro Poeta tenne certamente presente:

« Relinquitur quod creatio sit in instanti; unde, simul aliquid, dum creatur, creatum est, sicut simul illuminatur et illuminatum est »
[Si conclude che la Creazione fosse istantanea, cosicché una cosa nell'atto in cui la si crea è creata, a quel modo in cui quando si illumina una cosa, è illuminata] (Summa Contra Gentiles II, 19)

Il primo a mettere in dubbio l'idea che la propagazione della luce avvenisse a velocità infinita fu il solito Galileo Galilei. Questi inviò un discepolo con una lanterna coperta su una collina davanti a quella di Arcetri dove risiedeva, con la precisa istruzione di scoprire la lanterna quando avesse visto la luce della sua. A un certo punto Galileo scoprì la sua lanterna e tentò di misurare il tempo intercorso fra quell'atto e il momento in cui avrebbe visto la luce della lanterna del suo discepolo. A quel punto gli sarebbe bastato dividere il doppio della distanza fra le due colline per il tempo misurato, per ottenere la velocità della luce. Il ragionamento seguito era sicuramente corretto, ma purtroppo utilizzava una distanza troppo piccola, per percorrere la quale la luce impiegava una frazione di secondo, certamente non misurabile nella prima metà del Seicento. Ciò che Galileo misurava era in realtà il tempo di reazione del sistema nervoso del suo allievo che, quando vedeva la luce della lanterna del suo maestro, impiegava un certo tempo prima di scoprire la sua. Il grande scienziato pisano restò così con il dubbio se la velocità della luce fosse finita o infinita.

Giovanni Alfonso Borelli (1608-1679), discepolo di Galileo, compì il geniale tentativo di misurare la velocità della luce per mezzo di specchi riflettenti, sulla distanza Firenze-Pistoia, ma non ebbe miglior fortuna del suo maestro. Il primo a dimostrare che la velocità della luce è finita fu l'astronomo danese Ole Rømer (1644-1710), il quale si accorse che il periodo di rivoluzione dei satelliti di Giove variava nel corso dell'anno gioviano (pari a 11 anni e 315 giorni), apparendo maggiore quando Giove era più lontano dalla Terra (in congiunzione), e minore quando era più vicino (in opposizione). Rømer comprese genialmente che i ritardi erano dovuti al tempo impiegato dalla luce per percorrere il diametro dell'orbita terrestre, e stimò per primo la velocità della luce pari a circa 220.000 Km/s. In seguito Armand Hippolyte Fizeau (1819-1896) determinò la velocità della luce su distanze terrestri, usando una ruota dentata che girava ad alta velocità, ed ottenendo un valore di 315.000 km/s; dal canto suo Jean Bernard Léon Foucault (1819-1868) usò uno specchio rotante e stabilì che la velocità della luce era di 298000 km/s; egli riuscì anche a calcolare la velocità della luce in mezzi diversi dall'aria e dal vuoto. Oggi si ritiene che la velocità della luce nel vuoto sia di 299.792.458 m/s.

La misurazione della velocità della luce ebbe un'importanza straordinaria nel campo della Fisica Moderna. Prima di spiegarvi il perchè, voglio però attirare la vostra attenzione su uno dei tanti incontri fatti dall'Alighieri con spiriti più o meno bizzarri nel corso della sua avventura oltremondana. Nel Canto XVI del Purgatorio, Dante e Virgilio stanno attraversando la Terza Cornice del Purgatorio, e si ritrovano avvolti in un denso fumo. Appoggiandosi alla sua guida come fa un cieco, il Ghibellin Fuggiasco sente delle voci che cantano "Agnus Dei" e chiede a chi esse appartengano. Virgilio risponde che gli spiriti purganti immersi in quel fumo « d'iracundia van solvendo il nodo » (Purg. XVI, 24). Prima che Dante possa aggiungere alcunché, una voce gli domanda:

« Or tu chi se' che 'l nostro fummo fendi,
e di noi parli pur come se tue
partissi ancor lo tempo per calendi? » (Pur. XVI, 25-27)

A parlare è Marco Lombardo, uomo di corte della Marca Trevigiana a proposito del quale non si conoscono altre notizie che quelle fornite da Dante. Chiaro è il significato di questi versi: Dante parla di presente e di passato, come se per lui ci fosse ancora distinzione tra ciò che è già accaduto e cosa deve ancora accadere. Invece per l'anima di Marco Lombardo esiste ormai solo l'eternità, ed egli non può più dividere il tempo in calende, idi e none come facevano i Romani.

Proprio questa radicale differenza nella concezione del tempo secondo i due osservatori, Dante e Marco, ci porta diritto alla Relatività dei tempi, stabilita da Albert Einstein nel suo monumentale lavoro sulla Relatività Ristretta (1905). In pratica, mentre nella Relatività Galileiana viene postulato che due osservatori qualunque in moto reciproco uno rispetto all'altra misurino gli stessi tempi, e quindi che il tempo sia una realtà assoluta, Einstein giunge a conclusioni totalmente diverse. E qui ritorniamo alla questione della velocità della luce.

Fin dal 1887 infatti Albert Abraham Michelson (1852–1931) ed Edward Williams Morley (1838–1923) avevano condotto ripetutamente esperimenti per misurare con grande precisione la velocità della luce nella direzione del moto della Terra intorno al Sole e nella direzione esattamente contraria. Infatti la teoria elettromagnetica allora in voga predicava che le onde elettromagnetiche fossero vibrazioni dell'"etere", un materiale infinitamente elastico ed infinitamente trasparente che avrebbe dovuto permeare ogni cosa, fungendo da "riferimento assoluto" della Fisica Newtoniana: è evidente l'eredità del corrispondente termine aristotelico di cui abbiamo discusso nel capitolo precedente. Se l'etere fosse esistita, essa avrebbe dovuto restare ferma mentre la Terra orbitava in essa, e quindi, secondo le Trasformazioni Galileiane sopra scritte, la velocità della Terra nel suo moto orbitale (circa 33 Km/s) avrebbe dovuto sommarsi a quella della luce nella direzione del moto, e sottrarsi da essa in direzione opposta al moto del nostro pianeta. Invece, nonostante la loro esperienza fosse abbastanza accurata per rivelare questa differenza, Michelson e Morley trovarono sempre lo stesso valore della velocità della luce, in qualunque direzione essi la misurassero.

La conclusione era in aperto contrasto con ogni postulato della Fisica Classica, allora accettata per vera come il fatto che « non capere in triangol due ottusi » (Par. XVII, 15), tanto per usare le parole del nostro amato Dante. Per aggirare la difficoltà, Michelson e Morley supposero che la Terra trascinasse con sé una "nuvola" di etere, ma era evidente l'artificiosità di una tale spiegazione, anche perchè in tal caso l'etere avrebbe perso quelle caratteristiche pressoché metafisiche che gli scienziati dell'ottocento le avevano attribuito. A risolvere il problema fu proprio il ventiseienne Albert Einstein, allora oscuro impiegato dell'ufficio brevetti di Berna, il quale, nel suo studio datato 30 giugno 1905 ed intitolato « Zur Elektrodynamik bewegter Körper » ("Sull'Elettrodinamica dei corpi in movimento"), propose la rivoluzionaria teoria che la velocità della luce fosse la stessa in tutti i sistemi di riferimento.

Se si accetta per buono questo nuovo Postulato, bisogna buttare a mare gran parte della Fisica Classica su cui si basavano quasi tutte le conoscenze di allora. Infatti le Trasformazioni di Galileo non valgono più, e ad esse bisogna sostituire nuove trasformazioni oggi note come Trasformazioni di Lorentz. In un universo in cui queste ultime sono valide, tuttavia, le lunghezze e i tempi non sono più invarianti in tutti i sistemi di riferimento, contrariamente al senso comune accettato per buono da Galileo e da Newton. Ammettendo che l'unica vera invariante sia la velocità della luce, si scopre con sorpresa che le lunghezze si contraggono nella direzione del moto, e che osservatori in moto relativo l'uno rispetto all'altro percepiscono il trascorrere del tempo in modo diverso. Precisamente, un osservatore in moto con velocità v rispetto ad un altro registra un tempo t' che è legato al tempo t misurato dal primo osservatore mediante la formula:

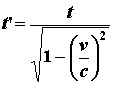
dove c è la velocità della luce. Ad esempio, per una navicella spaziale in moto rispetto alla Terra con una velocità di 180.000 Km/s, il rapporto v/c vale 3/5, e quindi la radice a denominatore della precedente assume il valore 4/5. Ciò significa che, mentre sulla Terra trascorre un'ora, per gli astronauti a bordo della navicella trascorrono 5/4 di ora, cioè 75 minuti. Per essi, quindi, il tempo è passato più lentamente (si parla in proposito di dilatazione dei tempi). Tuttavia, prima di mandare al macero tutte le opere di Galilei e di Newton, è facile rendersi conto del fatto che, se la velocità v assume valori su scala umana, infinitamente più bassi quindi della velocità della luce, il rapporto v/c tende a zero e la radice a denominatore della precedente tende ad 1; in altre parole, i due tempi tornano ad essere pressoché coincidenti. Ne consegue che la Fisica Classica è un'approssimazione della Fisica Relativistica di Einstein quando le velocità sono estremamente più basse di quella della luce.

Orbene, detto questo, non è difficile rendersi conto del fatto che Dante e l'anima purgante si ritrovano nella stessa situazione di due osservatori in moto relativo l'uno rispetto all'altro a velocità cosiddette relativistiche (cioè prossime a c): essi vivono in due tempi diversi. Le cose viste da entrambi sono le stesse, ma misurate in due modi differenti. Dante, come si vede, sembra essere riuscito ad anticipare persino la relatività dei tempi di Albert Einstein!!

Per saperne di più a proposito degli strani effetti della Relatività Ristretta, consultate quest'altro mio ipertesto didattico, intitolato « Il Treno di Einstein ». Per proseguire invece nel nostro viaggio attraverso la scienza dantesca, cliccate qui.