La statistica molecolare - La distribuzione maxwelliana - L'esperienza di Stern
Supponiamo di voler effettuare l'analisi di un sistema termodinamico, cioè di un gas. Com'è noto, esso è formato da un numero sterminato di molecole; in pratica, si tratta di un numero di Avogadro di esse. Un'analisi dinamica completa del suddetto sistema richiederebbe la determinazione della posizione e della velocità di ciascuna di queste molecole. Si tratta di due vettori per un totale di sei componenti: x, y, z, vx, vy, vz. Se le molecole sono N, si tratta di 6 N incognite. Per trovarle tutte serve un sistema di 6 N equazioni in 6 N incognite, rappresentate dalle equazioni classiche della dinamica. Occorrono anche 6 N condizioni iniziali, rappresentate dalle tre componenti della posizione iniziale e dalle tre componenti della velocità iniziale di ogni molecola. Concettualmente tale problema è risolubile ma, nella pratica, si tratta di un problema assurdo. Anche se la moderna tecnologia ha messo a disposizione buffer di memoria e processori con capacità di calcolo automatico un tempo ritenute da fantascienza, risolvere 1023 equazioni in 1023 incognite è veramente impossibile anche per il più ardito computer che la S.F. abbia mai osato immaginare. Pur ammettendo che ciò fosse possibile, tale calcolo richiederebbe comunque un tempo considerevolmente più lungo dell'età del nostro universo, senza tenere conto del fatto che, per ottenere questo po' po' di conoscenza, dovremmo a nostra volta saper misurare le posizioni e le velocità iniziali della suddetta molecola, e questo esula dalle possibilità pratiche.
È sufficiente conoscere qual è l'effetto globale che tutte quante quelle molecole, prese in un colpo solo, hanno sugli strumenti di misura. Infatti, se il gas è davvero formato da un grande numero di molecole, il volume V occupato da quel gas è rappresentato dallo spazio "spazzato" dalle molecole nel loro incessante moto di agitazione, e la sua pressione P sarà rappresentata dalla somma di tutti gli urti efficaci che esse esercitano contro le pareti del recipiente che le contiene. Tutto questo richiama per analogia un'altra situazione analoga: una popolazione molto numerosa di persone, di cui noi vogliamo conoscere gli usi e i costumi, o delle quali vogliamo conoscere la speranza di vita. In altre parole, ci ricorda la statistica demoscopica.
Il paragone è calzante: è infatti impossibile predire in che giorno, in che mese ed in che anno morirà un dato individuo, così come è impossibile calcolare quale saranno la posizione e la velocità di una certa particella in un determinato istante del futuro. E' però possibile conoscere la percentuale della popolazione che, in media, muoiono ad una data età; ed è sulla scorta di tali informazioni, che le compagnie di assicurazione calcolano i loro premi e le loro quote.
Allora, visto che un sistema termodinamico - come e più di una popolazione umana - è formata da un numero enorme di elementi, è possibile dedurre le informazioni necessarie per stabilire lo stato del sistema mediante una rilevazione statistica; tanto più che anche le grandezze da noi misurabili in laboratorio altro non sono se non valori medi calcolati su di una popolazione molto grande, com'è il caso della pressione o della temperatura. Di questo si occupa per l'appunto la Fisica Statistica, il nuovo ramo della Fisica creato da James C. Maxwell. Tale scienza si occupa di ricercare L'indagine statistica si disinteressa completamente della singola particella per valutare caratteristiche medie dell'intera popolazione, matematicamente traducibili nei valori medi (detti anche valori di aspettazione) delle grandezze in gioco, come l'energia cinetica posseduta dalle molecole, il numero medio delle molecole che hanno energie comprese tra due ben determinati valori, e così via. Ma, ed è importante ribadirlo, non si tratta di una soluzione di comodo, atta ad aggirare il problema senza risolverlo; essa risponde ad una precisa logica, alla quale - come accade nel caso dei censimenti - la Fisica deve necessariamente sottostare, allorché ha a che fare con popolazioni estremamente numerose e variegate. Tutto ciò che si può conoscere di esse sono i VALORI MEDI delle grandezze in gioco. E' importante sottolineare l'assoluta novità di questo metodo di indagine: l'evoluzione di un sistema non verrà più conosciuta con assoluta certezza, bensì solo in base alle leggi della probabilità, che sostituiscono quelle deterministiche tanto care alla meccanica classica. Viene meno il principio secondo cui, a partire da certe condizioni iniziali, la storia successiva del sistema è conosciuta univocamente; l'edificio concettuale su cui si basa l'intera Fisica è scosso dalle fondamenta, e gli scienziati sono costretti ad ammettere palesemente la loro ignoranza e la loro limitatezza di fronte alla pretesa superomistica di penetrare ogni segreto e di possedere i mitici libri della Sibilla, nei quali sarebbe contenuta una risposta ad ogni domanda, fosse anche la ricerca della posizione e della velocità di una singola molecola in mezzo ad un numero di Avogadro di sue simili. Questa rivoluzionaria novità spiega la diffidenza, se non il disprezzo ed il dileggio, con cui tale teoria venne inizialmente accolta, fino a condurre Ludwig Boltzmann al suicidio. A quell'epoca la concezione positivistica della scienza impediva di cogliere la portata ed il significato profondo della Fisica Statistica, e solo le successive ricerche sulla struttura granulare (atomica) della materia diedero definitivamente ragione a Maxwell e soci.
Cnsideriamo un sistema in equilibrio termodinamico, costituito da un numero molto grande di molecole, tutte indistinguibili tra di loro, e tale che tutte le configurazioni ipotizzabili possano essere assunte (ovvero, in altre parole, consideriamo un sistema il più caotico e disordinato possibile). Allora le velocità che le molecole possono assumere variano da zero fino a valori altissimi; se il sistema è all'equilibrio, si può pensare che la distribuzione delle velocità (cioè il numero delle particelle la cui velocità è compresa tra due valori assegnati) sia stazionaria, cioè che non muti nel tempo, fatte salve piccole e trascurabili fluttuazioni. Anzitutto, sebbene tutti i valori di velocità siano possibili, non tutti sono equiprobabili; si ha un massimo in corrispondenza di un certo valore, che dipende dallo stato termodinamico del sistema in esame. Maxwell riuscì genialmente a calcolare la distribuzione teorica delle velocità, distribuzione che oggi prende proprio il nome di Maxwelliana e che è espressa dalla formula:
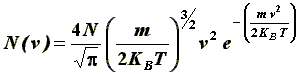
dove m è la massa della singola molecola, v è la sua velocità, KB è la costante di Boltzmann, T è la sua temperatura assoluta, N è il numero totale delle molecole in gioco, ed N (v) è il numero di molecole che hanno velocità compresa tra v e v + dv.
Rappresentandola
si nota che la curva di distribuzione non è simmetrica, a differenza per
esempio della celebre gaussiana. Infatti, mentre le velocità hanno un minimo
(lo zero), non hanno certamente alcun massimo; in teoria esse potranno tendere
all'infinito, anche se la probabilità che ciò avvenga tende progressivamente
allo zero. In realtà, pur non esistendo alcun limite classico alla velocità,
noi sappiamo che essa non potrà mai ne' superare ne' raggiungere la velocità
della luce; ma asteniamoci, almeno per ora, da qualsiasi considerazione
relativistica.
Inoltre, la distribuzione maxwelliana delle velocità dipende strettamente dalla temperatura del sistema; e questo corrisponde all'intuizione, perché al crescere della temperatura assoluta le molecole si fanno via via più veloci. Al crescere della temperatura il valore della velocità più probabile aumenta ed il numero medio di molecole che la possiedono diminuisce, provocando uno spostamento verso destra ed un appiattimento della distribuzione maxwelliana.
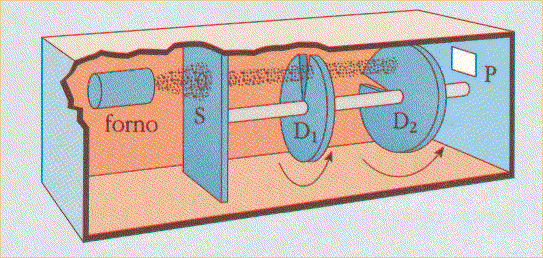
Come detto, non tutti i fisici accettarono queste conclusioni di natura statistica, che suscitarono un vivace dibattito fino al 1926, anno nel quale il fisico tedesco Otto Stern ebbe l'idea di verificare la teoria di Maxwell mediante un esperimento. Egli riscaldò del mercurio in un forno ad altissima temperatura, ottenendo un fascio perfettamente collimato che veniva iniettato in una camera sotto vuoto spinto, dove ruotano due dischi D1 e D2 calettati sullo stesso asse, e dotati di due fenditure sfasate l'una rispetto all'altra di un angolo noto. Fissata la velocità angolare dei dischi, risulta fissato l'intervallo di tempo necessario affinché una molecola che è passata attraverso la prima fenditura non sia intercettata dalla seconda. Solo le molecole dotate di una velocità tale da percorrere nello stesso tempo esattamente la distanza fra i due dischi, riescono ad oltrepassarli entrambi e a raggiungere il rivelatore P, che conta quante molecole sono passate. Regolando la velocità angolare dei dischi, è possibile regolare la velocità delle molecole che raggiungono indenni il rilevatore, e quindi, in ultima analisi, è possibile tracciare la funzione N = N (v). Stern verificò che tale distribuzione sperimentale coincide in maniera impressionante con la maxwelliana, fugando definitivamente ogni residuo dubbio sulla validità teorica della Fisica Statistica.
Argomenti correlati:
