L'intuizione di Faraday - Le equazioni di Gauss - La corrente di spostamento -
- E genera B, B genera E - Le onde elettromagnetiche
Noi abbiamo finora preso in considerazione gli studi di J.C.Maxwell riguardanti la termodinamica, e più precisamente la Teoria Cinetica dei Gas e la distribuzione oggi nota appunto come maxwelliana. Ma il suo contributo alla storia della scienza va ben al di là ed è incomparabile, grazie alla straordinaria sintesi che egli compì di un secolo di studi e ricerche sui fenomeni elettrici e magnetici, eseguite soprattutto dal grande Michael Faraday, ma anche da Gauss, Ampére, Oersted, Ohm e molti altri dei cui nomi oggi pullulano i libri di Fisica anche solo a livello divulgativo. Vediamo dunque come si giunse a tale sintesi, perché essa è fondamentale per capire l'ulteriore tappa del cammino dalla Fisica deterministica a quella probabilistica.
Faraday, come già Oersted, era convinto che tutte le forze della natura fossero tra loro connesse in qualche modo. Di conseguenza riteneva che l'elettricità ed il magnetismo non fossero due realtà separate che per pura combinazione esistevano nello stesso universo, ma fossero invece due diverse manifestazioni dello stesso fenomeno fondamentale. Questa convinzione metafisica, dello stesso tipo di quella che derivava dalle speculazioni di Schelling e degli altri Filosofi della Natura (Natürphilosophie) tedeschi dell'inizio del diciannovesimo secolo, aveva spinto Oersted a cercare in laboratorio quel collegamento tra elettricità e magnetismo, che aveva poi trovato effettivamente, scoprendo che la corrente elettrica circolante in un conduttore esercita una forza su un magnete vicino.
Anche Faraday credeva in un'unità fondamentale tra le forze della natura. Si può considerare la luce un'altra manifestazione di questa « forza » fondamentale o, per porre la questione con una terminologia più moderna, la luce è una forma di energia? Se così fosse, gli scienziati dovrebbero essere in grado di dimostrare sperimentalmente che esistono dei legami tra la luce e le altre forme di energia presenti nei fenomeni dell'elettricità e del magnetismo. Faraday riuscì in quest'impresa nel 1845, quando dimostrò che il piano di polarizzazione di un fascio di luce che attraversa un vetro di grande spessore ruota per effetto di un campo magnetico.
Essendosi convinto con questo esperimento dell'esistenza di un ben preciso legame tra luce e magnetismo, Faraday non seppe trattenersi dal suggerire arditamente che forse la luce stessa è una vibrazione delle linee di forza magnetiche! Si sa che tra due oggetti elettricamente carichi o magnetizzati passano delle linee di forza elettriche o magnetiche; allora, secondo il ragionamento di Faraday, se uno dei due oggetti si muove, si trasmette una perturbazione lungo le linee di forza. Inoltre, se le onde luminose sono generate dalle vibrazioni delle linee di forza, non è necessario immaginare che lo spazio sia pieno di una sostanza perfettamente elastica, cioè l'etere, per spiegare la propagazione della luce. Le linee di forza possono sostituire il concetto di etere, purché si dimostri che posseggono le proprietà elastiche necessarie per la trasmissione delle onde!
Faraday non era in grado di rendere questa idea più precisa perché non possedeva gli strumenti matematici necessari per dimostrare che le onde si possono propagare lungo le linee di forza elettriche o magnetiche. Altri fisici contemporanei sarebbero stati in grado di sviluppare una teoria matematica delle onde elettromagnetiche, ma essi non capirono il concetto di linee di forza proposto da Faraday, o perlomeno non lo considerarono sufficientemente valido per costruire una teoria matematica. Solo dieci anni dopo, il fisico matematico scozzese James Clerk Maxwell, che aveva appena completato gli studi alla Cambridge University, comprese il valore del concetto di linee di forza e riuscì a esprimerlo in forma matematica. Ed il risultato fu una delle più geniali costruzioni teoriche che la storia della Fisica ricordi.
I lavori di Oersted, Ampère, Henry e Faraday avevano stabilito due principi fondamentali dell'elettromagnetismo, poi sintetizzati da Carl Fredrich Gauss nei seguenti due teoremi:
1) Un corpo carico produce nello spazio circostante delle linee di forza elettriche, il cui flusso attraverso una superficie chiusa è pari alla somma delle cariche poste al suo interno divisa per la costante dielettrica.
2) Una corrente elettrica che circola in un conduttore produce delle linee di forza magnetiche attorno al conduttore, il cui flusso attraverso una superficie chiusa è sempre nullo.
La prima affermazione è matematicamente espressa dal Teorema di Gauss del campo elettrico:
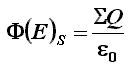
mentre la seconda viene detta anche Teorema di Gauss del campo magnetico:
Il primo teorema ha il seguente significato fisico: esiste il monopolo elettrico, cioè la carica elettrica singola, ed essa è sorgente o pozzo di campo elettrico a seconda che sia positiva o negativa. Il secondo teorema ci dice invece che il campo magnetico è solenoidale, ovvero che le linee di forza sono sempre chiuse, e NON esiste il monopolo magnetico. Spezzando un magnete in due, trovo sempre due magneti dotati entrambi di polo Nord e polo Sud. James Clerk Maxwell, negli anni tra il 1860 ed il 1870, sviluppò una teoria matematica dell'elettromagnetismo nella quale partì da questi due teoremi, oggi noti come PRIMA e SECONDA EQUAZIONE DI MAXWELL, in modo da poter determinare i campi elettrici e magnetici presenti nei conduttori, negli isolanti e anche nello spazio privo di materia.
Nel 1855, dopo aver completato da appena due anni gli studi liceali, Maxwell presentò alla Cambridge Philosophical Society un lungo articolo intitolato « Sulle linee di forza di Faraday », nel quale descriveva le proprietà delle linee di forza così come le aveva intuite il suo ingegnoso predecessore:
« ...se cominciamo da un punto qualsiasi e disegnamo una linea in modo tale che, spostandoci lungo di essa, la sua direzione coincida sempre con quella della forza risultante in ogni suo punto, questa linea curva indicherà, per ogni punto in cui passa, la direzione della forza e per questo motivo la si potrà chiamare una linea di forza.
Nello stesso modo potremo disegnare altre linee di forza, fino a quando avremo riempito tutto lo spazio con curve la cui direzione rappresenta quella della forza in ciascun punto. »
Maxwell affermò che il suo articolo aveva lo scopo di « mostrare come, applicando correttamente le idee e i metodi di Faraday, si poteva chiaramente rivelare, a chi conoscesse la matematica, il legame tra fenomeni di tipo cosi differente scoperti da Faraday stesso. »
Durante il decennio successivo, Maxwell elaborò una teoria per l'induzione elettrica e magnetica proponendo inizialmente un modello meccanico per visualizzare le relazioni esistenti tra le grandezze elettriche e magnetiche osservate sperimentalmente da Faraday e soci. In seguito Maxwell arrivò addirittura a descrivere il funzionamento del modello con un sistema di equazioni (oggi note come Equazioni di Maxwell) dalle quali si possono ottenere tutte le proprietà dei campi elettrici e magnetici. Queste equazioni davano una rappresentazione così efficace della teoria da rendere superfluo il modello meccanico delle linee di forza come corde elastiche, che alla fine fu abbandonato da Maxwell. Il lavoro di Maxwell contiene alcune idee completamente nuove e ricche di conseguenze:
a) un campo elettrico variabile nel tempo genera un campo magnetico.
b) non solo le correnti nei conduttori producono dei campi attorno ad essi, ma anche i campi elettrici variabili negli isolanti come il vetro o l'aria producono dei campi magnetici.
Anche
se si accetta facilmente l'esistenza di questo nuovo legame tra i campi
elettrici e magnetici, così come è stato formulato, è ben più difficile
accettare un nuovo ed importantissimo fenomeno previsto dalle equazioni di
Maxwell, ma che ai tempi dello scienziato scozzese non solo non era ancora noto,
ma non risultava neppure lontanamente immaginabile. Consideriamo un
isolante elettricamente neutro (per esempio un pezzo di vetro o di legno): esso contiene lo stesso numero di cariche positive e negative. Di solito queste
cariche sono distribuite uniformemente, cosicché la carica totale è zero in
ogni regione del materiale. Ma quando un isolante è posto in un campo
elettrico, queste cariche sono soggette a forze: le cariche positive sono spinte
in una direzione e quelle negative nella direzione opposta. Al contrario di
quanto avviene in un conduttore, le cariche presenti in un isolante non possono
allontanarsi sensibilmente dalle loro posizioni di equilibrio perché, non
appena subiscono un piccolo spostamento, nasce una forza di richiamo, dovuta
alla struttura interna dell'isolante stesso, che equilibra la forza prodotta dal
campo elettrico. Aumentando l'intensità del campo elettrico, anche le cariche
si sposteranno in misura maggiore. In particolare, se si applica a un isolante
un campo elettrico variabile, le cariche si spostano generando una corrente
variabile che Maxwell chiamò Corrente di Spostamento. Maxwell formulò
l'ipotesi che questa corrente di spostamento momentanea in un isolante sia in
grado di indurre nello spazio che la circonda un campo magnetico, proprio come
farebbe una corrente di conduzione. Il genio di Edimburgo avanzò
inoltre l'ipotesi che questo modello, sviluppato per la materia, fosse valido
anche per lo spazio
privo di materia (un'idea che a prima vista può sembrare
assurda), e che perciò in ogni caso un campo elettrico variabile nel tempo sia
circondato da un campo magnetico. Questo principio rappresentava un'ulteriore
previsione di Maxwell: precedentemente, infatti, si pensava che solo le correnti
in un conduttore potessero produrre un campo magnetico. L'ulteriore campo
magnetico che, secondo Maxwell, sarebbe stato generato da un campo elettrico
variabile, anche nello spazio vuoto, è così debole rispetto a quello prodotto
da una corrente in un conduttore che, a quei tempi, non era possibile misurarlo
direttamente. Ma Maxwell previde anche delle conseguenze che poterono ben presto
essere verificate.
L'esistenza della corrente di spostamento anche nello spazio privo di materia è giustificata dalla situazione illustrata nella figura qui sopra. Sia un circuito contenente un condensatore: in regime di corrente continua, il circuito risulta ovviamente aperto, non passa alcuna carica elettrica, e la circuitazione del campo elettrico calcolata lungo il percorso chiuso 1 è nulla sia prendendo in considerazione la superficie piana a che quella curva b, essendo nulla la corrente concatenata con le due superfici, cioè che le "buca" entrambe.
Diverso è il discorso se la corrente i è tempovariante. Infatti in questo caso il circuito dotato di condensatore non è chiuso, com'è ben noto, e la circuitazione del campo B lungo la linea l è pari, per il teorema della circuitazione di Ampére, al prodotto della corrente i per la permeabilità magnetica del vuoto µ0. Allora, tale circuitazione è pari a zero se si prende in considerazione la superficie b passante fra le armature del condensatore, non "bucata" da alcuna corrente di conduzione, ed è invece pari a µ0 i se si prende in considerazione la superficie a. Questo paradosso può essere risolto solo ammettendo l'esistenza, nello spazio vuoto tra le due armature, di una corrente che non è di conduzione, non essendoci cariche da spostare materialmente, ma che agli effetti del teorema della circuitazione di Ampére è equivalente ad una corrente di conduzione. Maxwell identificò tale corrente con la suddetta Corrente di Spostamento e, siccome essa dipende dalla rapidità con cui varia la posizione delle cariche, concluse che essa deve essere direttamente proporzionale alla rapidità con cui il campo elettrico varia nel tempo, o meglio dalla rapidità con la quale varia nel tempo il flusso del campo elettrico attraverso una superficie che ha come contorno il percorso l. E così il genio di Edimburgo attribuì ad essa la seguente espressione:
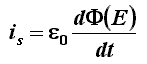
Di conseguenza la legge di Ampére-Maxwell sull'induzione magnetica, fino ad ora scritta nella forma C(B) = µ0 i, deve essere così modificata:
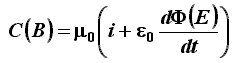
perchè alla corrente di conduzione i va aggiunta quella di spostamento is. Questa non viene più attribuita al solo André Marie Ampére ma, giustamente, è detta equazione di Ampére-Maxwell. e costituisce la TERZA EQUAZIONE DI MAXWELL.
Certamente questa ipotesi potrà apparire come un escamotage matematico volto a salvaguardare la veridicità del teorema di Ampére; la corrente è sempre stata intesa come un moto di cariche elettriche, siano essi elettroni (nei conduttori), ioni positivi e negativi (nelle soluzioni e nei gas), elettroni e lacune (nei semiconduttori); non si capisce dunque, a prima vista, come la formula che esprime is possa essere definita una corrente. Ad un esame più approfondito, invece, emerge il profondo significato fisico dell'ipotesi di Maxwell: essa ci dice che il campo magnetico che circonda la corrente di spostamento può essere considerato una conseguenza della variazione nel tempo del campo elettrico.
Secondo la teoria elaborata da Maxwell, insomma, i due principi fondamentali dell'elettromagnetismo, che abbiamo già ricordato poco sopra e che erano già stati stabiliti da altri scienziati, dovevano essere integrati da un terzo:
3) un campo elettrico variabile nello spazio produce un campo magnetico.
Il
vettore B del campo magnetico indotto sta in un piano perpendicolare al vettore
E del campo elettrico variabile e l'intensità di B dipende dalla rapidità con
cui varia E.
Consideriamo dunque una coppia di conduttori piani collegati a un generatore di corrente, come nella figura a sinistra. Mentre le cariche si avvicinano o si allontanano dai piatti attraverso i conduttori collegati alla corrente, l'intensità E del campo elettrico nello spazio tra i piatti varia nel tempo. Come si è già visto, questo campo elettrico variabile produce un campo magnetico nel quale l'intensità del vettore in un dato istante varia con la distanza dai piatti (naturalmente nella figura sono riportate solo alcune tra le infinite linee di forza di E e B). Cambiando segno alla carica sulle armature, e quindi il verso del campo elettrico da a) a b), anche le linee di forza del campo magnetico indotto cambiano verso. Questo è il significato fisico della Terza Equazione di Maxwell.
Un'altra proprietà dei campi elettrici e magnetici, già nota prima di Maxwell, acquista un nuovo significato alla luce del suo lavoro, poiché risulta simmetrica alla formulazione, enunciata poc'anzi, del terzo principio:
4) un campo magnetico variabile nello spazio produce un campo elettrico.
Il
vettore E del campo elettrico indotto sta in un piano perpendicolare al vettore
B del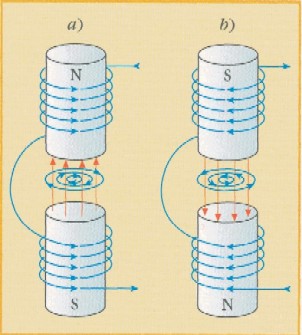
campo magnetico variabile, e l'intensità di E dipende dalla rapidità con
cui varia B. Osserviamo il campo magnetico variabile prodotto, per esempio, dal
momentaneo aumento della corrente in un elettromagnete, come quello nella figura
a destra. Questo campo magnetico
variabile induce un campo elettrico nella regione attorno al magnete. Se un
conduttore è allineato con la direzione del campo elettrico indotto, le cariche
elettriche libere nel conduttore si muoveranno per effetto del campo, producendo
una corrente nella stessa direzione del campo indotto. Anche in questo caso, invertendo
(da a) a b) in figura) le linee di forza del campo magnetico, anche quelle del
campo elettrico mutano verso.
Questo fenomeno di induzione elettromagnetica era stato scoperto sperimentalmente (manco a dirlo!) dal solito Faraday, ed infatti la legge matematica che la esprime è nota come equazione di Faraday-Neumann:
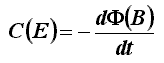
Essa significa che la circuitazione del campo elettrico indotto dal campo magnetico tempovariante è pari alla variazione nel tempo del flusso di tale campo magnetico induttore. Il segno meno indica che la corrente indotta ha segno opposto alla variazione di flusso che la produce, ed è nota come legge di Lenz. Essa rappresenta un caso particolare di una legge universale assai più generale, nota come principio di Le Chatêllier ed esprimibile in questi termini:
quando un sistema fisico viene perturbato, esso evolve nella direzione che tende a minimizzare la perturbazione avvenuta.
Infatti, quando il flusso di B varia nel tempo, viene indotta una corrente elettrica che a sua volta genera un campo magnetico, il cui flusso - per colpa di quel segno meno - varia in direzione opposta a quella del campo B esterno. In tal modo, se quest'ultimo sta diminuendo la corrente indotta cerca di sostenerlo, mentre se sta aumentarlo cerca di tamponarne la crescita. L'equazione di Faraday-Neumann e la legge di Lenz, prese assieme, costituiscono la QUARTA EQUAZIONE DI MAXWELL.
A partire dalle quattro equazioni di Maxwell testé scritte, è possibile ricavare in ogni punto il valore del campo elettrico e del campo magnetico, a patto di conoscere:
i) la distribuzione delle cariche nello spazio;
ii) la distribuzione delle correnti nei mezzi materiali o nel vuoto.
E' da notare come le nostre siano complesse equazioni integro-differenziali, e per essere risolte richiedano nozioni provenienti da corsi universitari. Si tratta comunque di equazioni di tipo assolutamente deterministico: note le condizioni iniziali e la distribuzione di cariche e di correnti, in ogni punto i campi E e B sono individuati con certezza. Essendo di tipo deterministico anche l'equazione di Newton F = m a (oggi nota come Secondo Principio della Dinamica), si deve concludere che la Fisica a fine '800 disegnava un quadro assolutamente meccanicistico del mondo in cui viviamo, se si fa eccezione per gli studi di Boltzmann e dello stesso Maxwell sulla Teoria Cinetica dei Gas, studi che infatti gli scienziati del tempo rigettarono perché non si allineavano agli indirizzi epistemologici della scienza "ufficiale". Come disse Wolfgang Goethe, « wir sind gewohnt dass die Menschen verhöhnen was sie nicht verstehen »: siamo abituati al fatto che gli uomini scherniscono ciò che non sono in grado di capire.
L'insieme completo di relazioni tra i campi elettrici e magnetici proposto da Maxwell non fu subito direttamente verificabile. Egli, però, aveva previsto anche un fenomeno affatto nuovo che avrebbe dovuto insorgere per effetto delle reciproche interazioni tra campi elettrici e magnetici variabili. Per capire di cosa si tratta, supponiamo che in una certa regione di spazio ad un certo istante si determini una variazione del campo elettrico, originato, per esempio, da un moto accelerato di cariche elettriche. Nei punti immediatamente vicini si produce allora, per la terza equazione di Maxwell, un campo magnetico anch'esso variabile nel tempo. La variazione del campo magnetico, per la quarta equazione di Maxwell, origina nei punti immediatamente vicini un campo elettrico anch'esso variabile, e così via. Nasce in tal modo una perturbazione elettromagnetica che si propaga nello spazio.
La perturbazione elettromagnetica può avere origine anche dalla variazione di un campo magnetico, causata, per esempio, da una variazione di corrente.
Supponiamo, per esempio, che l'intensità di corrente che percorre un filo, passi bruscamente da un certo valore i a zero; diminuisce di conseguenza il campo magnetico di questa corrente dal valore B, corrispondente al massimo valore della corrente, a zero. La variazione di B (quarta equazione di Maxwell) produce nei punti immediatamente vicini un campo elettrico variabile, che a sua volta genera nella regione circostante un campo magnetico variabile nel tempo e così via.
Il fatto che una variazione del campo magnetico in un punto produce un campo elettrico variabile era noto già prima di Maxwell, in quanto era previsto dalla legge di Faraday-Neumann; si pensava però che, allorché un campo magnetico bruscamente diminuiva da un valore massimo a zero, altrettanto doveva fare il campo elettrico e il tutto cessava dopo un piccolo intervallo di tempo dall'istante in cui si era annullato il campo magnetico. Il fatto nuovo previsto da Maxwell è proprio questo: i campi elettrico e magnetico generati dalla variazione nel tempo di uno dei due sono in grado di autosostenersi, cioè di propagarsi anche se la variazione iniziale che li ha prodotti p venuta meno!
Se ne conclude che, da una brusca variazione di un campo elettrico o magnetico nel tempo, ha origine la propagazione di un impulso elettromagnetico, così come da un rapido spostamento di un'estremità di una molla ha origine la propagazione di un impulso elastico che si propaga lungo tutta la molla. In altri termini la configurazione dei campi non è immobile, ma si propaga nello spazio, in modo che il valore del campo elettrico e del campo magnetico in un punto e ad un certo istante si ritrovano dopo un intervallo di tempo in altri punti vicini ad opportuna distanza.
Se si produce invece una variazione che dura nel tempo, eventualmente periodica, di un campo elettrico o magnetico in un punto, si origina conseguentemente la propagazione di una successione continua d'impulsi elettromagnetici, cioè un'ONDA che noi chiameremo per l'appunto onda elettromagnetica, nello stesso modo in cui, muovendo con continuità un'estremità di una molla tesa, si genera un'onda elastica che si propaga lungo tutta la molla.
Le onde elettromagnetiche sono onde trasversali: il campo elettrico ed il campo magnetico, infatti, oltre ad essere sempre ortogonali tra loro, sono sempre perpendicolari anche alla direzione di propagazione, come illustra la figura seguente:
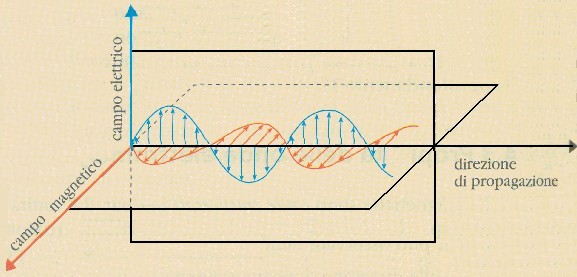
I vettori E e B misurati in un punto e ad un determinato istante formano, insieme con la direzione di propagazione, una terna destrorsa, ossia una terna di vettori tale che un osservatore disposto lungo la direzione di propagazione che riceve frontalmente i campi vede sempre E alla sua destra e B alla sua sinistra. In altri termini, le direzioni di E, di B e quella di propagazione sono tali che una vite destrorsa, disposta perpendicolarmente al piano di E e di B, mentre ruota nello stesso verso secondo cui deve ruotare E per sovrapporsi a B, avanza nella direzione di propagazione dell'onda elettromagnetica.
La direzione del campo elettrico E in un punto, e conseguentemente anche quella del campo magnetico, in generale può variare col tempo, mantenendosi però sempre ortogonale alla direzione di propagazione; se invece la direzione di E non varia, l'onda elettromagnetica è polarizzata rettilineamente. Una proprietà notevole delle onde elettromagnetica, che consegue direttamente dalle equazioni di Maxwell, è la seguente: il campo elettrico e quello magnetico sono sempre in fase fra loro. Inoltre, assieme all'onda elettromagnetica si ha anche una propagazione di energia con la stessa velocità dell'onda.
Lo stesso Maxwell dedusse teoricamente dalle sue celebri equazioni che le onde elettromagnetiche si propagano nel vuoto con velocità c, data dalla formula:
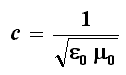
dove ε0 = 8,859 · 10-12 F m-1 rappresenta la costante dielettrica del vuoto, e µ0 = 12,56 · 10-7 H m-1 è la permeabilità magnetica del vuoto. Sostituendo nella formula precedente i valori delle due costanti ho:
c = 2,9979 · 108 m s-1 ≈ 300.000 Km s-1
Il valore della velocità di propagazione delle onde elettromagnetiche nel vuoto coincideva dunque con buona approssimazione con quello della velocità della luce, già noto dalle esperienze di Fizeau e Foucault. Questo fu un risultato clamoroso che mise in evidenza lo straordinario potere unificante delle equazioni di Maxwell.
Egli, avendo notato che le onde elettromagnetiche e la luce, oltre ad essere caratterizzate entrambe da vibrazioni trasversali, si propagano con la stessa velocità, avanzò l'ipotesi della natura elettromagnetica della luce, e così l'ottica divenne un capitolo dell'elettromagnetismo. E scusate se è poco.
Argomenti correlati:
La nascita dell'Elettromagnetismo (lettura)
