![]()
|
« Ritengo che potremo partire in settemila, tra fanti e cavalieri... » (SdA, libro V, cap. IX) |
A differenza di quanto si è detto nel capitolo precedente, la Fisica non è fatta solo di strumenti di misura e di sistemi di numerazione. Essa deve anche trattare una grande mole di dati sperimentali, ed è per questo che ha bisogno degli strumenti della Statistica. Non a caso è stato detto che questa disciplina è stata ideata « per interrogare la Natura e per verificare le ipotesi »: ad esempio, una misura sperimentale dell'accelerazione di gravità terrestre non può essere effettuata una volta sola, nel timore che gli errori (sistematici o casuali) inficino il risultato. Più volte la misura verrà ripetuta, e più veritiero sarà il risultato che se ne ottiene. Dobbiamo perciò procedere a quella che viene chiamata un'analisi statistica dei risultati. Il più semplice esempio di "statistica" nell'ambito del "Signore degli Anelli" è rappresentata dalla "distribuzione" degli anelli nella celeberrima poesiola di otto versi contenuta nel capitolo II del Primo Libro de "La Compagnia dell'Anello", e il cui sesto e settimo verso sono incisi nel Linguaggio Nero proprio sull'Anello Dominante, del quale indicano lo scopo:

Come si vede, in questo breve brano si parla di venti anelli, forgiati nella notte dei tempi su istigazione di Sauron, che aspirava a diventare il signore del mondo. Di questi, 3 sono per i re degli Elfi, 7 per i Nani, 9 per gli Uomini e 1, l'unico appunto, per l'Oscuro Signore. Questi 20 anelli costituiscono una popolazione statistica: tale termine designa l'insieme di tutti gli individui oggetto dell'indagine, mentre ogni oggetto viene detto unità statistica. Naturalmente l'analisi statistica ha tanto più senso, quanto più alto è il numero delle unità statistiche. I venti anelli citati nella filastrocca testé riportata possono sembrare pochi rispetto ad un'analisi statistica, ma quest'ultima è adattissima a un censimento. Nella saga di Tolkien ne troviamo uno nel capitolo XIV del "Quenta Silmarillion", intitolato "Il Beleriand e i suoi regni". In essi, pur senza citare numeri espliciti, il Professore di Oxford esplicita un vero e proprio censimento degli Elfi, suddividendoli per stirpi e regioni geografiche in cui si sono stanziati:
«
Ecco la distribuzione delle contrade cui vennero i Noldor, situate nelle regioni
nordoccidentali della Terra di Mezzo, nei giorni antichi [...] Fingolfin e
Fingon suo figlio reggevano lo Hithlum e la
maggior parte delle genti di
Fingolfin abitavano nel Mithrim, sulle rive del Grande Lago... »
(QS, cap. XIV)
Un elenco numerico vero e proprio, che può essere oggetto di indagine statistica, lo ritroviamo invece ne "Il Ritorno del Re", e precisamente nel passo in cui, vinta la Battaglia dei Campi del Pelennor, Aragorn, Éomer e Gandalf decidono di portare la guerra davanti al Cancello Nero di Mordor:
«
Disse Gandalf: "Non ti consiglio di lasciare la Città del tutto indifesa.
[...] Chiedo quindi ai Capitani: quante forze possiamo radunare e avviare, al
più tardi fra due giorni? E devono essere uomini valorosi che partano
volontariamente, consci del pericolo."
"Sono tutti stanchi, e molti hanno subito ferite più o meno gravi",
disse Éomer, "e abbiamo avuto ingenti perdite di cavalli, il che è
difficile da rimediare. Se dobbiamo partire presto posso sperare di condurre
tutt'al più duemila uomini,
lasciandone appena altrettanti a difesa della Città."
"Non dobbiamo calcolare soltanto quelli che hanno combattuto su questo
campo", disse Aragorn. "Stanno giungendo nuove forze dai feudi del
Sud, ora che le coste sono libere. Ne ho inviati quattromila da Pelargir
attraverso il Lossarnach due giorni addietro, ed Angbor l'Intrepido cavalca in
testa. [...] Ritengo che potremo partire in settemila,
tra fanti e cavalieri, pur
lasciando la Città meglio difesa di quanto non fosse all'inizio
dell'assalto." »
(SdA, libro V, cap. IX)
Le proprietà delle unità che saranno oggetto della nostra indagine statistica si diranno caratteri. I caratteri possono essere quantitativi o variabili e qualitativi o mutabili, a seconda che essi possano essere espressi tramite numeri oppure no. Ad esempio, il colore dei cappucci dei Nani o la razza a cui appartengono i membri dell'armata che si oppongono a Sauron sono caratteri qualitativi; la quantità di erba pipa fumata da un Hobbit in un mese o il numero dei caduti ogni giorno nella guerra contro l'Oscuro Signore sono caratteri quantitativi. Inoltre le variabili si distinguono a loro volta in discrete e continue. Le prime possono assumere solo i valori di un insieme che possono essere numerati, cioè posti in corrispondenza biunivoca con l'insieme dei numeri naturali; le seconde invece possono assumere valori qualsiasi. Tipicamente, le variabili discrete sono quelle che risultano da un'operazione di conteggio; ad esempio, il numero dei figli in ogni famiglia di Hobbit, oppure l'età (avanzatissima) a cui è morto ogni Re di Númenor. Le variabili continue invece derivano tipicamente da misurazioni, come quelle che hanno luogo in Fisica. Questo è il caso dell'altezza in centimetri di un Hobbit, o della temperatura della lava del Monte Fato. Facciamo un esempio. Consideriamo una popolazione di Nani, e si consideri come carattere il loro casato di appartenenza. Le modalità sono: Casato di Durin, di Dwalin, di Thràr, eccetera: è un carattere di tipo qualitativo. Oppure, si consideri la quantità di pancetta consumata in un anno da un Hobbit di Sottocolle. La popolazione è costituita dagli abitanti di Sottocolle, ovviamente; Il carattere è quantitativo continuo, e le modalità sono tutti i possibili valori indicati dalla bilancia usata per massare la pancetta.
Di ogni modalità che può essere assunta da un carattere occorre misurare le frequenze. Si chiama frequenza assoluta il numero di volte in cui quella modalità è stata osservata. Ad esempio, nella Compagnia dell'Anello vi sono uno Stregone, due uomini, quattro Hobbit, un nano e un elfo; ne consegue che questi numeri rappresentano le frequenze con cui ciascun carattere (la razza) si presenta nella Compagnia. Si dice invece frequenza relativa di una modalità il rapporto tra la frequenza assoluta e il totale della popolazione. Nel semplice caso da noi preso in esame, i membri della Compagnia sono 9 in tutto (quanti i Nazgû), per cui la frequenza relativa degli uomini è 2/9, quella degli Hobbit è 4/9, e così via. Naturalmente la statistica ha senso per numeri più alti di quelli dei membri della Compagnia. Un esempio può essere rappresentato dalle frequenze delle parole nei romanzi di Tolkien, ricavate da questo sito. Ecco alcuni esempi (S. = Silmarillion; H. = Hobbit; CdA = la Compagnia dell'Anello; lDT = le Due Torri; RdR = il Ritorno dei Re):
| Parola |
S. |
H. |
CdA |
lDT |
RdR |
| Bilbo | 0 | 549 | 321 | 8 | 32 |
| Elfo |
54 |
26 |
76 |
35 |
34 |
| Gandalf | 1 | 187 | 458 | 337 | 299 |
| Gollum | 0 | 96 | 69 | 328 | 23 |
| Hobbit |
0 |
173 |
410 |
260 |
132 |
| Mordor |
14 |
0 |
62 |
68 |
93 |
| Nano | 18 | 45 | 56 | 40 | 17 |
| Sauron |
177 |
0 |
59 |
34 |
47 |
Consideriamo ad esempio le frequenze assolute (fa) della parola "Nano" nei cinque libri suddetti. Per ricavare le frequenze relative (fr) basta sommare tutte le frequenze assolute e poi dividere ciascuna di esse per il totale, cioè 176. Moltiplicando ognuna di esse per 100, abbiamo le frequenze percentuali (f%):
| . |
S. |
H. |
CdA |
lDT |
RdR |
Tot. |
| fa | 18 | 45 | 56 | 40 | 17 |
176 |
| fr | 0,102 | 0,256 | 0,318 | 0,227 | 0,097 | 1 |
| f% | 10,2 % | 25,6 % | 31,8 % | 22,7 % | 9,7 % | 100 % |
Delle frequenze si danno spesso rappresentazioni grafiche, sotto forma di diagrammi a torta, a barre, eccetera. Ecco ad esempio un diagramma a torta che illustra le frequenze della parola "Nano":

Esistono però anche le frequenze cumulate. Cosa sono? Si tratta della somma delle frequenze assolute di tutte le modalità minori o uguali di quella considerata. Per capire di cosa stiamo parlando, consideriamo le lunghezze dei capitoli de "Lo Hobbit", misurate attraverso il numero di parole dell'originale inglese, come indicate nel sito sopra citato. Considereremo non tutti e 19 i capitoli del romanzo, ma solo i primi sei:
|
.Cap. |
I |
II |
III |
IV |
V |
VI |
| Parole | 8638 | 5257 | 2876 | 4034 | 6967 |
6703 |
Questo significa che chi legge "Lo Hobbit", arrivando alla fine del primo capitolo "Una festa inaspettata" ha letto 8638 parole. Chi arriva alla fine del secondo capitolo "Abbacchio arrosto", ha letto altre 5257 parole, ma dall'inizio del romanzo ha letto 8638 + 5257 = 13.895 parole. Giunti alla fine del terzo capitolo "Un breve riposo", sono state lette altre 2876 parole, e quindi dall'inizio sono state lette 8638 + 5257 + 2876 = 16.771 parole; e così via. Queste sono le frequenze cumulate (fc):
|
.Cap. |
I |
II |
III |
IV |
V |
VI |
| fa | 8638 | 5257 | 2876 | 4034 | 6967 |
6703 |
| fc | 8638 | 13.895 | 16.771 | 20.805 | 27.772 | 34.475 |
Appare facile intuire come stavolta sia più utile un diagramma a linee, che mostra di quanto "crescono" le frequenze dall'inizio verso la fine del romanzo. L'ultimo valore della frequenza cumulata, dopo 19 capitoli, è il totale delle parole, cioè l'intera lunghezza del romanzo!


Come si vede, trattare decine o addirittura centinaia di valori non è semplice, e non solo per una questione di calcolo, che ai nostri giorni può essere velocizzato facendo uso del supporto informatico, e in particolare del foglio elettronico. Da quella marea di numeri infatti bisogna estrarre dei valori significativi, che "a colpo d'occhio" ne sintetizzino il significato, e per questo sono detti valori di sintesi. In particolare sono stati introdotti i valori di sintesi noti come valori di posizione. Il caso più semplice è rappresentato dalla media aritmetica, sulla quale non è il caso di soffermarsi, poiché tutti sappiamo in cosa consiste. Vale piuttosto la pena di precisare i casi in cui la media aritmetica NON è la più adatta da usare per "riassumere" il significato dei dati tabulati. A rendersene conto in maniera magistrale fu il poeta romanesco Trilussa (1871-1950) nel seguente, famosissimo sonetto:
« Sai
ched'è la statistica? È 'na cosa
che serve pe fà un conto in generale
de la gente che nasce, che sta male,
che more, che va in carcere e se sposa.
Ma pe' me la statistica curiosa
è dove c'entra la percentuale,
pe' via che, lì, la media è sempre eguale
puro co' la persona bisognosa.
Me spiego: da li conti che se fanno
seconno le statistiche d'adesso
risurta che te tocca un pollo all'anno:
e, se nun entra nelle spese tue,
t'entra ne la statistica lo stesso
perch'è c'è un antro che ne magna due. »
Si prenda in considerazione in proposito il seguente esempio. Come si legge nel seguente brano, le armate di orchi di Sauron andavano crescendo di giorno in giorno:
«
Frodo e Sam osservarono quell'odiosa terra [Mordor] con un misto di antipatia e
di ammirazione. Fra loro e la montagna fumante e tutt'intorno ad essa, ogni cosa
pareva morta e distrutta, un deserto arido e sconvolto. Si chiesero come facesse
il signore di quel paese a mantenere ed a nutrire i suoi schiavi ed i suoi
eserciti. Eppure, ne aveva parecchi. Sino a perdita d'occhio, lungo le falde del
Morgai e giù a sud, si stendevano gli accampamenti, alcuni di tende, altri
ordinati come piccole città. Uno dei più grandi si trovava proprio sotto di
loro. Copriva circa un miglio di pianura, simile a un enorme nido d'insetti, con
tetre strade diritte fiancheggiate da capanne e da lunghi e bassi edifici.
Tutt'intorno la terra era piena di gente che andava e veniva; un'ampia strada
conduceva dall'accampamento verso sudest, raggiungendo la via di Morgul, e molte
file di piccole figure nere le percorrevano velocemente [...] Qui l'Oscuro
Potere, muovendo i suoi eserciti come pedine, era intento a radunarsi. »
[SdA, libro VI, cap. II)
Supponiamo dunque che, nell'anno 1418 del Calendario della Contea (l'anno in cui Frodo giunge a Gran Burrone e viene deciso di costituire la Compagnia dell'Anello), nel mese di novembre le truppe di Orchi crescano di numero del 21 % rispetto al mese di ottobre, e nel mese di dicembre crescano del 44 % rispetto al mese di novembre. Qual è la media delle due crescite?
Una risposta ben poco intelligente sarebbe: del 32,5 %, valore ottenuto sommando 21 % e 44 %, e dividendo il risultato per due. Infatti, come aveva intuito Trilussa, la definizione di media tra due valori è la seguente: è il valore che avrebbe dovuto essere tenuto durante tutto il periodo di tempo considerato, onde ottenere lo stesso risultato finale. Se ad esempio il cavallo Ombromanto (del quale parleremo nel capitolo seguente) procede a 30 miglia all'ora per due ore e a 50 miglia all'ora per altre due, in tutto ha percorso 30 x 2 + 50 x 2 = 160 miglia in 4 ore, e per ottenere questo risultato avrebbe dovuto procedere per l'intero intervallo di tempo a 40 miglia all'ora; dunque, in questo caso la media aritmetica tra 30 e 50 rappresenta il calcolo corretto. Non così invece nel calcolo relativo all'esercito di Sauron. Sia infatti N il numero degli effettivi di tale armata nel mese di ottobre 1418. Se in novembre tale numero è cresciuto del 21 %, ciò significa che il totale rappresenta il 121 % del mese precedente, e quindi può essere indicato con 1,21 x N. Nel mese di dicembre gli effettivi crescono del 44 % rispetto a novembre, e diventano quindi 1,44 volte più del mese che precede. Tale numero potrà essere perciò espresso come 1,44 x 1,21 x N. Sia T il tasso di crescita che dovrebbe essere uguale a novembre e a dicembre, affinché si ottenga lo stesso risultato. In base a quanto detto sopra il numero di Orchi di Sauron del mese di dicembre deve essere pari a:
( 1 + T ) x ( 1 + T ) x N = ( 1 + T )2 x N
Da qui si deduce l'equazione:
1,44 x 1,21 x N = ( 1 + T )2 x N
N si semplifica, e si ottiene che è pari alla radice quadrata di 1,44 x 1,21, cioè a 1,32. Ne consegue che il tasso T cercato deve essere pari al 32 %. Ne consegue che, per arrivare a questo risultato, l'operazione necessaria non è la media aritmetica, bensì la media geometrica, definita in generale mediante la formula:
![]()
In altri casi, neppure la media geometrica va bene. Ad esempio, se si considerano due resistenze elettriche disposte in serie, la media aritmetica tra di esse è l'operazione corretta per determinare la resistenza media equivalente. Se invece le resistenze sono in parallelo, per trovarne il valore medio occorre eseguirne la media armonica, definita come l'inverso della media aritmetica degli inversi dei valori considerati. Il nome di media armonica è dovuto al matematico greco Archita di Taranto (428-347 a.C.), e deriva dal fatto che le corde vibranti che producono l'accordo perfetto do-mi-sol hanno lunghezze che stanno tra di loro in modo che quella centrale è la media armonica delle altre due. Tale media è molto influenzata dai valori piccoli, mentre la media aritmetica è influenzata piuttosto dai valori grandi.
Un'altra media frequentemente utilizzata è la cosiddetta media pesata (o ponderata), in cui ogni valore entra con un particolare peso, diverso da quello degli altri. In altre parole, ad ogni valore x1, x2, ..., xn è associato rispettivamente un peso f1, f2, ..., fn, in cui la scelta della lettera f rimanda direttamente al concetto di frequenza. La formula che fornisce la media pesata di tali valori è:

Per capirne il significato, si consideri il seguente caso. Supponiamo che la ricchezza media degli abitanti di Minas Tirith, la capitale del Regno di Gondor, fosse di mille monete pro capite, e quella di Edoras, la capitale del Regno di Rohan, di duecento monete pro capite. Affermare però che "la ricchezza media delle due città è di seicento monete pro capite", perchè ( 1000 + 200 ) / 2 = 600 è un clamoroso errore che si ritrova persino su quotati quotidiani economici! Il motivo consiste nel fatto che Minas Tirith ed Edoras non hanno certo la stessa popolazione. Come si è detto, infatti, il valore medio è quello che conserva il totale; calcoliamo dunque questo totale. Supponiamo che la prima avesse diecimila abitanti, e la seconda mille. Ne consegue che la ricchezza totale degli abitanti di Minas Tirith è pari a 1000 x 10000 = dieci milioni di monete, mentre quella totale degli abitanti di Edoras è di 200 x 1000 = duecentomila monete, per un totale di dieci milioni e duecentomila monete. Dividendole per la popolazione totale delle due città, cioè 11.000 abitanti, si ottengono circa 927 monete a testa. Come si vede, quest'operazione è il risultato di una media pesata, in cui 10.000 abitanti è il peso delle 1000 monete e 1000 abitanti è il peso delle 200 monete. Come si vede, stavolta a dominare è il valore con il peso più importante.
Un altro esempio è il calcolo della temperatura media. Si supponga che ad Hobbiville si registrino 10° di temperatura per 36 giorni all'anno, 11° per 22 giorni all'anno, 12° per 28 giorni all'anno, e così via. Per trovare la temperatura media non basta certo calcolare la media aritmetica delle temperature: occorre infatti moltiplicare ogni temperatura per il corrispondente peso, cioè per il numero dei giorni dell'anno durante i quali essa è registrata, sommare i prodotti e dividere il risultato per i 365 giorni dell'anno. Oggi la media pesata è adoperata ad esempio nei conti correnti bancari, in cui i calcoli vengono fatti attraverso di essa: ad esempio, per 20 giorni sul conto corrente teniamo 12.000 euro, poi depositiamo su di esso 4.000 euro e per 15 giorni teniamo 16.000 euro, quindi preleviamo 1.000 euro e teniamo 15.000 euro per 10 giorni... 20 giorni è il peso di € 12.000, 15 giorni è il peso di € 16.000, 10 giorni è il peso di € 15.000, e così via. La banca calcola la media pesata di tutti questi valori, e fa pagare le tasse su tale media. Anche la speranza di vita alla nascita è il risultato di una media ponderata.
La media aritmetica riveste un particolare valore in Fisica, dove le misure possono essere dirette o indirette. Le prime sono eseguite leggendo direttamente il valore su di uno strumento di misura, ad es. la durata di un fenomeno sul cronometro, o la corrente che attraversa un circuito su di un amperometro. Le seconde invece vanno determinate attraverso calcoli, essendo impossibile il confronto diretto con un'unità di misura: è il caso della misura dell'altezza di una montagna, della distanza in anni luce di una stella da noi, della densità di una sostanza solida. Ora, è facile verificare che, ripetendo innumerevoli volte una misura indiretta, non si ritroverà MAI lo stesso valore, ma i risultati ottenuti saranno distribuiti dentro un intervallo, che di solito viene indicato con la parola inglese range. Ciò è dovuto a due tipi possibili di errori: sistematici e casuali. Gli errori sistematici sono dovuti a cause contingenti, come un cronometro che rimane indietro o uno strumento mal tarato, oppure da difetti della vista dello sperimentatore o dalla sua inesperienza. In genere tali errori sono tutti per eccesso o tutti per difetto; essi possono essere eliminati, sostituendo lo strumento di misura con uno più preciso o lo sperimentatore con uno più esperto. Gli errori casuali (o stocastici) non possono essere eliminati, essendo dovuti per l'appunto ad una distribuzione statistica dei valori attorno ad un valore medio. Ovviamente è più probabile rilevare valori prossimi a questo valore medio, piuttosto che valori eccessivamente piccoli o eccessivamente grandi, per cui la distribuzione di questi valori non è uniforme. Immaginiamo ad esempio di aver misurato l'altezza del pinnacolo di Orthanc, con un procedimento simile a quello utilizzato nel capitolo precedente per trovare l'altezza della Torre Oscura, oppure con qualche altro metodo indiretto, ad esempio la misurazione dell'ombra della torre e la proporzione con l'ombra di un bastone di lunghezza nota. Ripetendo 50 volte la misura, si ottengono i seguenti 50 valori in ranga (che, come si è detto, è un'unità di misura númenoreana di lunghezza):
|
275,4 |
258,8 |
279,6 |
318,6 |
303,5 |
|
284,9 |
347,7 |
284,1 |
292,6 |
277,3 |
|
281,0 |
311,1 |
286,9 |
315,2 |
308,7 |
|
308,2 |
291,1 |
275,2 |
299,9 |
272,4 |
|
315,1 |
251,6 |
288,8 |
294,0 |
285,8 |
|
301,6 |
294,9 |
316,7 |
285,0 |
316,2 |
|
309,9 |
258,5 |
305,5 |
295,0 |
260,8 |
|
251,0 |
286,1 |
290,5 |
335,3 |
304,2 |
|
325,3 |
309,1 |
293,9 |
288,0 |
307,8 |
|
269,1 |
294,4 |
308,5 |
332,2 |
278,3 |

Il pinnacolo di Orthanc in una ricostruzione artistica
Come si vede, il valore più piccolo fornisce 251,0 rangar, mentre il massimo è di 347,7. Il loro valore medio è h = ( 275,4 + 258,8 + 279,6 + ... + 278,3 ) / 50 = 296,1 rangar. Dividiamo ora questi dati in gruppi; nel primo poniamo i valori compresi tra 250 (incluso) e 260 (escluso) rangar, nel secondo i valori compresi tra 260 (incluso) e 270 (escluso) rangar, e così via, fino all'ultimo dei dieci gruppi, compreso fra 340 (incluso) e 350 (escluso) rangar. Al primo gruppo appartengono due valori, al secondo altri due, al terzo sei, al quarto nove, e via discorrendo. Un modo molto comodo per rappresentare questi dati consiste in un istogramma, cioè un grafico che riporta il numero di elementi di ogni gruppo sotto forma di barre verticali affiancate:

Quando il numero delle misure diventa grandissimo (500, 5000, 50.000...), e quindi anche il numero dei gruppi in cui essi sono suddivisi cresce sempre più, tutte le distribuzioni sperimentali come quella in esame passano dal discreto al continuo, ed assumono sempre la stessa tipica forma a campana, data dalla curva gaussiana, così detta in onore del grande matematico tedesco Carl Friedrich Gauss (1777-1855). Non solo l'errore commesso durante una misura, ma anche l'usura delle parti di un dispositivo meccanico, lo scarto del punto d'impatto di un proiettile rispetto al bersaglio, la lunghezza dei rivetti prodotti da una macchina a controllo numerico, l'altezza e il peso della popolazione di bambini iscritti a una scuola elementare, le variazioni giornaliere dei prezzi di chiusura di un'azione, il tempo che intercorre fra gli arrivi dei voli in un aeroporto, il tempo necessario per servire un cliente in un negozio di abbigliamento, il tempo di caricamento di un sito Internet... sono tutti esempi di grandezze i cui valori rispettano una distribuzione gaussiana. Un caso famoso riguarda il bombardamento di Londra da parte dei nazisti durante la Seconda Guerra Mondiale: una volta una V2 tedesca colpì una caserma, e tra i britannici si diffuse il panico. Possibile che i tedeschi sapessero mirare con tanta precisione da colpire un obiettivo militare a 300 km di distanza? L'analisi dei siti dove erano cadute le V2 tuttavia rivelò che il numero di bombe cadute nei riquadri in cui la mappa di Londra era stata divisa seguiva una distribuzione gaussiana, cioè governata puramente dal caso, e quindi il bombardamento della caserma era stato un evento accidentale.
L'istogramma inoltre mostra chiaramente come la maggior parte delle misure sia compresa tra 270 e 320 rangar, mentre i valori maggiori di 320 e minori di 270 rangar siano molto più rari. Inoltre questi valori sono disposti in modo pressoché simmetrico rispetto al valor medio centrale, che dunque rappresenta anche la mediana, cioè il valore che lascia tante misure a destra quante a sinistra. Ciò significa che gli errori per difetto e quelli per eccesso si presentano con la stessa probabilità, e che quindi è corretto considerare come valore più attendibile la media aritmetica dei nostri 50 valori. Tuttavia, in Fisica affermare che "la torre di Orthanc è alta 296,1 rangar", cioè 285 metri e 79 centimetri, non sarebbe corretto. Tale misura è infatti manifestamente affetta da un errore. In prima approssimazione, tale errore può essere valutato attraverso la semidispersione, che rappresenta la metà della differenza tra il valore massimo ed il valore minimo tra quelli tabulati:
Δh = (347,7 – 251,0 ) / 2 = 48,3 rangar
Di conseguenza la misura in Fisica viene espressa in questo modo:
h = ( 296,1 ± 48,3 ) rangar
Quello qui introdotto è un errore assoluto; ma non sempre esso è significativo. Ad esempio, un errore assoluto di un centimetro su una lunghezza totale di venti centimetri rivela che la misura è stata piuttosto grossolana, mentre un errore assoluto di un centimetro su un totale di venti metri caratterizza una misura estremamente precisa. Per questo conviene introdurre l'errore relativo, dato dal rapporto tra errore assoluto e valore più attendibile della misura, e l'errore relativo può essere espresso anche in termini di percentuale. Nel caso sopra riportato, ad esempio, Δh/h = 48,3 / 296,1 = 0,163, il che corrisponde a un errore percentuale del 16,3 %, piuttosto consistente.

I valori di posizione però da soli non bastano, e sarà facile rendersene conto con un esempio. Si considerino quattro Nani che possiedono rispettivamente 220, 250, 150 e 180 monete d'oro. Nessuno di essi è ricco sfondato, e la media dei loro averi è ( 220 + 250 + 150 + 180 ) / 4 = 800 / 4 = 200 monete d'oro. Siano invece altri quattro Nani, che possiedono rispettivamente 50, 330, 380 e 40 monete d'oro. In questo caso due sono decisamente poveri mentre due sono straricchi, eppure la media dei loro averi è ( 50 + 330 + 380 + 40 ) / 4 = 800 / 4 = 200 monete d'oro: la stessa di prima! Le due distribuzioni sono completamente diverse, eppure il loro principale valore di posizione è lo stesso. Per questo sono stati introdotti, oltre ai valori di posizione, anche i valori di variabilità. Essi ci dicono quanto, in media, i valori tabulati si discostano dal valore medio x, cioè dalla media aritmetica dei valori suddetti. Il più semplice di questi valori di variabilità potrebbe essere la media aritmetica delle differenze tra le modalità della variabile x e la loro media x. Tuttavia, basterà un esempio per renderci conto che tale scelta non è la più felice. Considerati infatti i quattro valori sopra riportati 220, 250, 150 e 180. Sottraendo loro la media 200, si hanno i quattro valori + 20, + 50, – 50 e – 20, la cui media aritmetica è palesemente ( 20 + 50 – 50 – 20) / 4 = 0. E non è una coincidenza: si può dimostrare che la media degli scarti dal valor medio è sempre nulla. E allora?
La soluzione adottata dalla statistica è la seguente. Calcoliamo la media non degli scarti dal valore medio, ma dei loro quadrati; tale risultato è noto come varianza, e la si indica con σ2. Nel nostro caso, ad esempio, si devono elevare al quadrato i quattro scarti, ottenendo [ 202 + 502 + ( – 50 )2 + ( – 20 )2 ] / 4 = ( 400 + 2500 + 2500 + 400 ) / 4 = 5800 / 4 = 1450. La radice quadrata di questo valore prende il nome di scarto quadratico medio o deviazione standard, lo si indica con σ e nel nostro caso vale circa 38. Questo significa che, in media, i valori della prima distribuzione di ricchezze si allontanano in media di 38 dal valore medio. Proviamo ora con la seconda distribuzione di valori. Sottraendo a 50, 330, 380 e 40 il loro valore medio 200 si hanno – 150, + 130, + 180 e – 160. Troviamo la varianza: [ ( – 150 )2 + 1302 + 1802 + ( – 160 )2 ] / 4 = ( 22.500 + 16.900 + 32.400 + 25.600 ) / 4 = 97.400 / 4 = 24.350, decisamente più elevata del caso precedente. La sua radice quadrata fornisce circa 156; ciò significa che i valori della distribuzione considerata distano in media 156 dal valore medio, cioè più di quattro volte rispetto alla distribuzione precedente! Ciò vuol dire che i quattro patrimoni dei primi quattro Nani sono tutti addensati intorno al loro valor medio, mentre quelli degli altri quattro si trovano molto più lontani da esso! Ecco come potrebbero apparire le due distribuzioni di monete, se prendessimo in considerazione ogni volta non quattro, ma quattrocento Nani, e passassimo dal discreto al continuo, rappresentando le distribuzioni assegnate come curve gaussiane:

Quella blu è la prima distribuzione, più addensata intorno alla media; quella rossa è la seconda, con i valori mediamente più lontani da x. In pratica, σ è una stima di metà larghezza della distribuzione, ed infatti qualcuno la chiama anche FWHM (Full Width High Middle), ovvero "piena larghezza a metà altezza", perchè tale "mezza larghezza" è valutata a metà dell'altezza del massimo centrale. La formula generale per il calcolo della varianza σ2 è la seguente:

Si può dimostrare che la formula precedente può essere sostituita da questa, più semplice da utilizzare:

Nel secondo dei casi da noi usati come esempio, si ha [ ( 502 + 3302 + 3802 + 402 ) / 4 ] – 2002 = 24.350. Come si vede, i conti tornano.
Se applichiamo lo stesso metodo alla misura della torre di Orthanc che abbiamo utilizzato sopra, troveremo che in quel caso σ2 = 388 e σ = 19,7. Se la distribuzione è effettivamente gaussiana, si può dimostrare che il 68,3 % delle misure è compreso fra h – σ ed h + σ, cioè nel nostro caso fra 296,1 – 19,7 = 276,4 rangar e 296,1 + 19,7 = 315,8 rangar. A questo punto come stima dell'errore assoluto Δh possiamo usare proprio σ, ottenendo così una stima ben più precisa della precedente:
h = ( 296,1 ± 19,7 ) rangar
L'errore percentuale infatti stavolta vale Δh/h = 19,7 / 296,1 = 0,066, il che corrisponde a un errore percentuale del 6,6 %, ben più contenuto della grossolana stima fatta sopra.

Un ruolo importante, nella Statistica, è ricoperto dalle cosiddette Tabelle a Doppia Entrata, che sono alla base della Statistica Bivariata, nella quale si studiano congiuntamente due caratteri X ed Y, allo scopo di mettere in luce eventuali relazioni tra di esse. Un esempio molto semplice è costituito dal seguente. Delle tre stirpi di Eldar, i Vanyar, i Noldor ed i Teleri, non tutti parteciparono alla Guerra d'Ira contro Morgoth. Ne consegue che il carattere X della nostra statistica sarà la stirpe degli Elfi, mentre il carattere Y consisterà nel fatto di aver combattuto o meno contro l'Oscuro Signore. Considerando che i Vanyar erano la stirpe meno numerosa e i Teleri quella più consistente, prendiamo in considerazione un campione di 800 elfi. Essi potranno essere così distribuiti:
|
Frequenze |
Hanno |
Non hanno |
Totale |
|
Vanyar |
Vanyar che |
Vanyar che non |
Vanyar |
|
Noldor |
Noldor che |
Noldor che non |
Noldor |
|
Teleri |
Teleri che |
Teleri che non |
Teleri |
|
Totale |
Eldar
che |
Eldar che non |
Eldar |
Quella che abbiamo costruito qui sopra è una tabella a doppia entrata, perchè i dati entrano dall'alto, distinguendo tra chi ha combattuto e chi no, e anche da sinistra, distinguendo tra le tre stirpi di Elfi. Ogni coppia di modalità ( X ; Y ) avrà la sua frequenza assoluta, indicata nella tabella. La tabella tuttavia presenta una riga in più, sotto le tre principali, nella quale si inseriscono le somme delle frequenze di ogni colonna, e una colonna in più, a destra delle due principali, nella quale si inseriscono le somme delle frequenze di ogni riga. Tali somme, inserite nei "margini" della tabella, vengono dette frequenze marginali. Essi rappresentano delle "somme parziali", ed i loro significati sono stati scritti dentro le corrispondenti caselle della tabella. In pratica, la colonna sulla destra evidenziata in verde fornisce i numeri dei rappresentanti delle tre stirpi di Eldar, mentre la riga in basso evidenziata in azzurro fornisce il numero di quanti hanno combattuto e quanti no. Infine, in basso a destra c'è una cella evidenziata in rosso, nella quale compaiono le somme di entrambe le serie di frequenze marginali. Come si può verificare, entrambe le somme danno come risultato (com'è logico) il numero complessivo di Elfi da noi considerato. In pratica, le righe e le colonne marginali forniscono le distribuzioni che si otterrebbero se ciascuno dei due caratteri considerati fosse studiato singolarmente.
Se poi consideriamo una sola colonna della tabella soprastante, potremo osservare come il carattere X si distribuisce tra le unità statistiche che manifestano una certa modalità di Y. Ad esempio, la prima colonna ci dice quanti sono i Vanyar, i Noldor e i Teleri che hanno combattuto contro Morgoth. Si parla in tal caso di frequenze condizionate; condizionate, naturalmente, dalla modalità considerata. Fissare l'attenzione su una singola riga o colonna della nostra tabella significa dunque restringersi alla sottopopolazione che presenta una singola modalità di X o di Y. Tale singola riga o colonna equivale a una distribuzione univariata, per la quale vale tutto il discorso da noi fatto sopra. Da notare che le tabelle a doppia entrata possono essere sostituite con una rappresentazione a diagrammi di Venn, quindi insiemistica. Tutta la statistica anzi può essere riscritta per mezzo della Teoria degli Insiemi.
Lo studio congiunto di due caratteri X ed Y può però essere finalizzato ad uno scopo ben preciso: decidere se fra le due variabili esiste una qualche relazione di dipendenza, cioè se una è funzione dell'altra. A questo scopo, l'idea migliore è quella di confrontare le distribuzioni marginali di X condizionate alle modalità di Y con la distribuzione marginale di X, che esprime il comportamento di X considerato singolarmente. Se le due variabili sono indipendenti tra di loro, c'è da aspettarsi che il condizionamento di X alle modalità di Y non abbia alcun effetto, ovvero che le distribuzioni condizionate si mantengano uguali a quella marginale. C'è però un problema: le frequenze marginali si riferiscono all'intera popolazione, mentre le frequenze condizionate si riferiscono solo alla sottopopolazione relativa alla modalità rispetto alla quale stiamo condizionando. Non dobbiamo dunque lavorare con le frequenze assolute, ma con quelle relative. Diremo perciò che il carattere X è indipendente dal carattere Y se le frequenze relative condizionate di X rispetto alle modalità di Y sono uguali alle frequenze relative marginali di X.
Si può dimostrare che due caratteri X e Y, di cui state osservate le modalità x1, x2, ..., xn e y1, y2, ..., yn su una popolazione costituita da n unità, sono tra di loro indipendenti se e solo se, per ogni i = 1, 2, ..., h e per ogni j = 1, 2, ..., h, si ha:

In pratica, essa equivale a dire che ogni frequenza congiunta deve essere uguale al prodotto delle corrispettive frequenze marginali, diviso per n. Da questo consegue il fatto che la relazione di indipendenza è simmetrica: X è indipendente da Y solo se Y lo è da X. Le frequenze congiunte che soddisfano la condizione di indipendenza sopra scritta vengono chiamate frequenze teoriche di indipendenza, per distinguerle da quelle effettivamente misurate, e le si indica con fT(xi,yj). Ad ogni tabella a doppia entrata è dunque associare una tabella teorica di indipendenza, che si costruisce tenendo fisse le frequenze marginali e sostituendo le frequenze congiunte misurate con quelle teoriche di indipendenza. Se le due tabelle coincidono, allora si ha perfetta indipendenza statistica. Consideriamo a mo' di esempio la tabella vista sopra che esprime la partecipazione delle tre stirpi di Elfi alla Guerra d'Ira, e costruiamo la tabella delle frequenze teoriche di indipendenza. Ad esempio, la frequenza teorica dei Vanyar che hanno combattuto contro Morgoth si ottiene moltiplicando il totale dei Vanyar, cioè 100, per il numero totale degli Elfi che hanno combattuto, cioè 480, e dividendo il prodotto per 800, che è il totale degli Elfi da noi considerati. Avremo così 100 x 480 / 800 = 60, che coincide con il numero dei Vanyar che hanno effettivamente combattuto. Proseguendo in questo modo avremo la seguente tabella teorica di indipendenza:
|
Frequenze |
Hanno |
Non hanno |
Totale |
|
Vanyar |
480
x 100 / 800
= |
320
x 100 / 800
= |
100 |
|
Noldor |
480
x 300 / 800
= |
320
x 300 / 800
= |
300 |
|
Teleri |
480
x 400 / 800
= |
320
x 400 / 800
= |
400 |
|
Totale |
480 |
320 |
800 |
Come si vede, solo due delle sei frequenze teoriche coincidono con le corrispondenti frequenze misurate effettivamente, per cui la tabella ora costruita non combacia con quella di partenza, e dunque le due variabili non risultano statisticamente indipendenti. Ciò significa che l'appartenenza a una stirpe piuttosto che all'altra ha una qualche influenza sulla disponibilità o meno a combattere contro l'Oscuro Signore, ed infatti abbiamo visto che i Noldor corsero ad arruolarsi in massa,, mentre i Teleri non furono altrettanto entusiasti:
«
L'esercito dei Valar si apprestava alla battaglia; e sotto i suoi candidi
vessilli marciavano i Vanyar, il popolo di Ingwë, nonché quelli dei Noldor
che mai avevano abbandonato Valinor e alla testa dei quali era Finarfin figlio
di Finwë. Ben pochi dei Teleri erano desiderosi di andare alla guerra, memori
com'erano del fratricidio al Porto dei Cigni e del ratto delle loro navi; ma
finirono per prestare orecchio a Elwing, che discendeva dalla loro stessa
stirpe, sicché mandarono marinai in numero sufficiente per governare le navi
che portarono le schiere di Valinor a est, di là dal mare. Restarono però a
bordo dei loro vascelli, e nessuno di loro mise piede sulle Terre-di-qua. »
(QS, cap. XXIV)
Da notare che, mentre le frequenze rilevate sono sempre espresse da numeri interi, quelle teoriche di indipendenza in generale non lo sono (quello soprastante è stato un caso fortunato), dal momento che scaturiscono da rapporti. Anche però ammettendo che le frequenze teoriche siano tutte espresse da numeri interi, la situazione di perfetta indipendenza statistica è un caso molto raro che si verifica solo raramente, e va quindi considerato come una situazione ideale. Ciò che ci interessa conoscere realmente è: quanto i dati reali si discostano dalla perfetta indipendenza? In altre parole, noi vogliamo conoscere il grado di dipendenza, o meglio di correlazione, come si dice nel linguaggio della statistica, tra due variabili X ed Y. Tale grado sarà tanto più elevato, quanto più la tabella delle frequenze rilevate si discosta da quella delle frequenze teoriche di indipendenza. I principali valori di sintesi che misurano tale scostamento si devono perciò basare sulle differenze tra le frequenze rilevate e quelle teoriche, differenze che vengono chiamate contingenze e sono così definite:
c(xi,yj) = f(xi,yj) – fT(xi,yj)
Si può dimostrare che la somma delle contingenze è sempre pari a zero, come la media degli scarti dal valore medio; per questo, per esprimere con un unico valore di sintesi tutte le differenze, non è possibile limitarsi a sommare le contingenze. Il valore di sintesi più usato è stato introdotto dal matematico britannico Karl Pearson (1857-1936) e, come la varianza e lo scarto quadratico medio, si basa sui quadrati delle contingenze, e viene chiamato "chi quadro" perchè lo si indica con la lettera greca chi (χ):

In pratica, per calcolare il chi quadro occorre determinare tutte le contingenze, elevarle al quadrato e dividerle per le corrispondenti frequenze teoriche di indipendenza, quindi sommare tutti i risultati ottenuti; la doppia sommatoria significa che le somme devono includere gli addendi provenienti da tutte le frequenze congiunte della tabella a doppia entrata. Questo valore di sintesi è pari a zero se e solo se tutte le contingenze sono nulle, cioè se le frequenze teoriche combaciano perfettamente con quelle osservate, e quindi si ha perfetta indipendenza statistica, mentre cresce al crescere delle contingenze. Il valore del chi quadro può essere calcolato più rapidamente usando la seguente formula semplificata, più facile da usare:
In pratica, bisogna elevare al quadrato ogni frequenza congiunta e dividerne il quadrato per il prodotto delle corrispondenti frequenze marginali, sommare tutti i risultati ottenuti, sottrarre uno e moltiplicare il risultato per n. Troviamo ad esempio il valore del χ2 nel caso degli Elfi che hanno combattuto contro Morgoth:
χ2 = 800 x [ 602/(480 x 100) + 402/(320 x 100) + 2502/(480 x 300) + 502/(320 x 300) + 1702/(480 x 400) + 2302/(320 x 400) – 1 ] = 800 x [ 0,075 + 0,05 + 0,434 + 0,026 + 0,151 + 0,413 – 1 ] = 800 x 0,1489 = 119
Si presenta ora il problema di interpretare il chi quadro. Il valore ora trovato, 119, è alto o basso? In altre parole, indica l'esistenza di una dipendenza forte o debole? Per rispondere a queste domande occorre "normalizzare" l'indice, cioè trasformarlo in un numero compreso tra 0 e 1, in modo da poterlo interpretare più facilmente. Per far questo, basterà dividere χ2 per il suo valore massimo, cioè il valore che assumerebbe in caso di perfetta correlazione; ma quanto vale, questo valore massimo? Si può dimostrare che tale valore è pari al prodotto tra n, il numero complessivo di unità statistiche considerate, e il minimo tra ( h – 1 ) e ( k – 1 ), dove k ed h rappresentano rispettivamente il numero di modalità differenti dei caratteri X ed Y. Nel caso sopra considerato, k = 3, h = 2 ed n = 800; tra 3 – 1 = 2 e 2 – 1 = 1 il minimo è rappresentato da 1, per cui il valore massimo di χ2 è pari ad 800 x 1 = 800. Il χ2 normalizzato perciò vale 119 / 800 = 0,149 = 14,9 %. Il grado di correlazione tra le stirpi di Eldar e l'aver partecipato o meno alla guerra contro Morgoth è appena del 15 %: un grado piuttosto basso, almeno nell'esempio da noi ipotizzato.
Un altro valore di sintesi molto usato per valutare la correlazione tra caratteri quantitativi è la cosiddetta covarianza, indicata con il simbolo σXY e così definita:
dove x ed y sono i valori medi di X ed Y. Per capirne il significato, interpretiamola geometricamente. Immaginiamo di rappresentare in un piano cartesiano i punti di coordinate (xi; yi), con i = 1, 2, ..., n. Otterremo una distribuzione di punti, disposti intorno a (x; y); tracciamo le rette x = x ed y = y, cioè le parallele agli assi cartesiani passanti per tale punto. Queste due rette dividono il piano cartesiano in quattro quadranti, che numeriamo in senso antiorario come si vede in figura. Nel quadrante I, i valori di x sono maggiori di x, e quindi si ha x – x > 0, e i valori di y sono maggiori di y, per cui y – y > 0. Il loro prodotto risulterà perciò positivo, e porremo un + nel quadrante. Nel quadrante II, invece, i valori di x sono minori di x, e quindi si ha x – x < 0, mentre i valori di y sono maggiori di y, per cui y – y > 0. Il loro prodotto risulterà perciò negativo, e indicheremo il quadrante con un –. Nel quadrante III, i valori di x sono minori di x, e quindi si ha x – x < 0, ed anche i valori di y sono minori di y, per cui y – y < 0. Il loro prodotto risulta positivo, e indicheremo il quadrante con un +. Infine, nel quadrante IV i valori di x sono maggiori di x, e quindi si ha x – x > 0, mentre i valori di y sono minori di y, per cui y – y < 0. Il loro prodotto è perciò negativo, e indicheremo il quadrante con un –. Per maggior chiarezza:

Se dunque la covarianza è positiva, la maggior parte dei prodotti ( xi – x ) ( yi – y ) è positiva, quindi la maggior parte dei punti di coordinate (xi ; yi) deve cadere nei quadranti I e III; la distribuzione dei punti avrà perciò la forma mostrata nella figura sottostante, e suggerisce una relazione di tipo lineare crescente tra X ed Y:

Se invece la covarianza è negativa, la maggior parte dei prodotti ( xi – x ) ( yi – y ) è negativa, quindi la maggior parte dei punti di coordinate (xi ; yi) deve cadere internamente ai quadranti II e IV; la distribuzione dei punti avrà perciò la forma mostrata nella figura qui sotto, e suggerisce una relazione di tipo lineare decrescente tra X ed Y:

Se invece la covarianza è pressoché nulla, i punti sono sparpagliati senza alcuna regolarità apparente, oppure sono disposti secondo relazioni molto diverse da quella lineare, ad esempio quadratica o logaritmica.
Così come per il chi quadro, anche per la covarianza esiste una formula più semplice da applicare per determinarne il valore:

Anche in questo caso, per stabilire se la correlazione tra X ed Y sia forte o debole occorre normalizzare la covarianza dividendola per il suo valore massimo. In questo caso si può dimostrare che la covarianza di due variabili X ed Y può assumere solo valori compresi entro il seguente intervallo:
![]()
dove σX e σY sono rispettivamente gli scarti quadratici medi di X e di Y. Diremo allora coefficiente di correlazione lineare, o coefficiente di Pearson-Bravais, indicato con ρ, il rapporto:
Per come è stato definito, risulta sempre – 1 < ρ < + 1. Il segno del coefficiente di correlazione lineare è lo stesso della covarianza, e fornisce informazioni analoghe:
ρ > 1 indica una correlazione lineare crescente;
ρ < 1 indica una correlazione lineare decrescente;
ρ = 0 indica l'assenza di una correlazione lineare.
Tanto più ρ è vicino a ± 1, tanto più l'approssimazione con una correlazione lineare è buona, e tanto più i punti corrispondenti ai valori rilevati si addensano lungo una retta; tanto più ρ è prossimo a zero, tanto più i punti se ne discostano. Di solito se 0 < ρ < 0,3 si parla di correlazione lineare debole; se 0,3 < ρ < 0,7, si parla di correlazione lineare media; se 0,7 < ρ < 1, si parla di correlazione lineare forte. Ecco un esempio di alcune distribuzioni di valori con i rispettivi valori di ρ (le prime due sono correlazioni negative, le ultime due positive):


Vogliamo ora vedere un esempio numerico. Consideriamo la Battaglia dei Campi del Pelennor, magistralmente raccontata nel capitolo VI del V libro del SdA, uno di quelli in cui più il romanzo assume i toni di un poema epico:
«
Ad un tratto il re Théoden gridò qualcosa a Nevecrino, e il cavallo balzò
avanti. Alle sue spalle sventolava il vessillo: un cavallo bianco in campo
verde, ma egli lo distanziò. Dietro di lui galoppavano come fulmini i
cavalieri della sua scorta, senza però riuscire a raggiungerlo. [...] La
furia guerriera dei suoi avi scorreva come fuoco nelle sue vene, ed egli
cavalcava Nevecrino come un antico dio, come Oromë il Grande nella Battaglia
dei Valar quando il mondo era giovane. Il suo scudo dorato, scoperto, brillava
e scintillava come un'immagine del Sole, e l'erba rinverdiva intorno ai piedi
bianchi del suo destriero. Il mattino arrivò, e arrivò anche il vento del
mare; e l'oscurità scomparve, e gli eserciti di Mordor tremarono, e furono
colti dal terrore, e fuggirono, e morirono, e zoccoli furibondi li
calpestarono. Allora tutto l'esercito di Rohan irruppe in un canto, e
cantavano mentre colpivano, in preda alla gioia della battaglia, ed il suono
del loro canto fiero e terribile giunse sino alla Città. »
(SdA, libro V, cap. V)
L'"Atlante della Terra di Mezzo" ci fornisce lumi circa le forze in campo. Gondor ha fornito circa 5000 soldati fra fanti, arcieri e cavalieri, cui vanno aggiunti 200 soldati di Lossarnach guidati da Forlong, 300 soldati della Valle di Ringlò guidati da Dervorin, 6000 cavalieri di Rohan guidati da Théoden ed Éomer, 1200 soldati di Dol Amroth guidati da Imrahil e almeno 2000 tra fanti e arcieri provenienti da altri alleati e feudi del Sud. Da notare che ad essi si opponevano più di 100.000 tra Orchi, Uruk-hai, Haradrim ed uomini provenienti dalle terre di Khand e di Rhûn, comandati dal Re Stregone di Angmar. Concentriamoci tuttavia su Aragorn e sui suoi alleati. Le perdite umane alla fine della maggior battaglia di tutta la Terza Era ammontarono più o meno a 3.000 uomini di Gondor, tra i quali Hirluin il Bello, Forlong il Vecchio, Derufin e Duilin, 2.000 Rohirrim tra i quali Re Théoden, e possiamo stimare ad occhio 80 caduti di Lossarnach, 150 caduti al comando di Dervorin. 550 di Dol Amroth e 750 tra gli altri alleati (le armate di Mordor invece furono quasi interamente distrutte).

Gandalf contempla le armate di
Mordor che muovono all'as-
sedio di Minas Tirith ne "Il Ritorno del Re" di Peter Jackson
Vogliamo determinare il coefficiente di correlazione lineare tra il numero di effettivi e quello dei caduti di ogni schiera sui Campi del Pelennor. Tabuliamo anzitutto i dati che abbiamo elencato sopra:
|
.Nazione |
Soldati |
Caduti |
|
Gondor |
5000 | 3000 |
|
Lossarnach |
200 | 80 |
|
Valle di Ringlò |
300 | 150 |
|
Rohan |
6000 | 2000 |
|
Dol Amroth |
1200 | 550 |
|
Altri |
2000 | 750 |
Il numero degli effettivi rappresenterà il carattere quantitativo X, quello dei caduti il carattere quantitativo Y. Per trovare il coefficiente di correlazione tra di essi occorre determinare gli scarti quadratici medi σX e σY e la covarianza σXY di X ed Y. Appare conveniente organizzare i dati in una tabella:
|
xi |
yi |
xi yi |
xi2 |
yi2 |
| 5000 | 3000 | 15.000.000 | 25.000.000 | 9.000.000 |
| 200 | 80 | 16.000 | 40.000 | 6400 |
| 300 | 150 | 45.000 | 90.000 | 22.500 |
| 6000 | 2000 | 12.000.000 | 36.000.000 | 4.000.000 |
| 1200 | 550 | 660.000 | 1.440.000 | 302.500 |
| 2000 | 750 | 1.500.000 | 4.000.000 | 562.500 |
| 14.700 | 6.530 | 29.221.000 | 66.570.000 | 13.893.900 |
Nell'ultima riga abbiamo posto le somme di tutte le colonne soprastanti. A questo punto possiamo calcolare tutti i parametri che ci servono:
x = Σ xi / 6 = 14.700 / 6 = 2450
y = Σ yi / 6 = 6530 / 6 = 1088,3
σX2 = Σ xi2 / 6 – x2 = 66.570.000 / 6 – (2450)2 = 5.092.500
σY2 = Σ yi2 / 6 – y2 = 13.893.900 / 6 – (1088,3)2 = 1.131.180,6
σXY = Σ xi yi / 6 – x y = 29.221.000 / 6 – (2450 x 1088,3) = 2.203.750
σX è pari alla radice quadrata di 5.092.500, cioè a 2256,66, mentre σY è pari alla radice quadrata di 1.131.180,6, cioè a 1063,57. Se ne conclude che, nel nostro caso, il coefficiente di correlazione lineare vale:
ρ = 2.203.750 / ( 2256,66 x 1063,57 ) = 0,918
Quindi il numero di soldati e il numero di caduti sono legati al 92 % da una correlazione lineare.
Quanto detto però non è sufficiente. Infatti, dopo aver scoperto l'esistenza di una relazione lineare tra le variabili X ed Y, vogliamo scrivere la funzione lineare che meglio interpreta tale relazione. Consideriamo dunque una generica funzione lineare di equazione y = m x + q. Per ogni punto Pi(xi,yj) che appartiene alla distribuzione assegnata, consideriamo il corrispondente punto Qi(xi,yj') di ascissa xi come Pi, appartenente alla retta y = m x + q. Tracciamo quindi i segmenti P1Q1, P2Q2, ..., PnQn, ottenendo una figura di questo tipo:
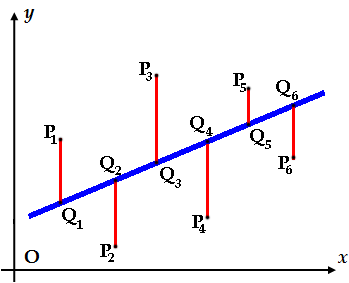
La lunghezza del generico segmento PiQi è pari a |yi – yi'|. Eleviamo al quadrato tali lunghezze e sommiamole, ottenendo Σi ( yi – yi' )2. Questa somma esprime in modo semplice ed efficace una misura dello scarto complessivo fra i dati osservati yi e i valori teorici yi', determinati sul grafico della retta. Come funzione lineare che meglio approssima i dati, scegliamo quella per la quale questa somma Σi ( yi – yi' )2 risulta minima. Questa retta prende il nome di retta di regressione. Si può dimostrare che l'equazione di tale retta è:
y – y = m ( x – x )
Il suo coefficiente angolare m si dice coefficiente di regressione, ed è dato dalla formula seguente:
Determiniamo dunque l'equazione della retta di regressione nel caso dei caduti durante la Battaglia dei Campi del Pelennor. Già sappiamo che x = 2450 e che y = 1088,3. Calcoliamo con la formula (4) m = 2.203.750 / 5.092.500 = 0,433. Abbiamo così l'equazione y – 1088,3 = 0,433 ( x – 2450 ), cioè:
y = 0,433 x + 27,45
Confrontiamo i dati rilevati nella tabella soprastante con quelli generati mediante questa formula:
|
.x |
5000 |
200 |
300 |
6000 |
1200 |
2000 |
| y | 3000 | 80 | 150 | 2000 | 550 |
750 |
| y' | 2192,4 | 114 | 157,3 | 2625,4 | 547 | 893,4 |
Come si vede, alcune "previsioni" sono particolarmente accurate, mentre i valori più alti sono quelli che più si discostano dai valori teorici. Questo tipo di analisi può essere applicato ad un numero inimmaginabile di situazioni; ad esempio, in un elenco di coppie che si sono sposate nel Primo Anno della Quarta Era, si può cercare se vi è una correlazione lineare tra l'età della moglie e quella del marito. Oppure, si può verificare se, in una edizione delle Olimpiadi, prendono più medaglie le squadre delle nazioni più popolose, come la Cina, o quelle delle nazioni con il più alto prodotto interno loro pro capite, come Stati Uniti d'America o Germania (in teoria, più abitanti ha un paese, più numerosi possono essere gli atleti e quindi i medagliati, ma se la popolazione più numerosa non può permettersi di andare in palestra ad allenarsi, è difficile ottenere certi risultati). In una classe, può essere fondamentale cercare se vi è una correlazione lineare tra i voti presi da ogni alunno nelle diverse discipline, per verificare se lo studente considerato è selettivo, o ottiene buoni risultati nella maggior parte delle materie. A questo proposito, per correlare tra di loro più di due variabili statistiche si utilizza una matrice di correlazione ρij, una matrice quadrata simmetrica di dimensione n x n che ha sulle righe e sulle colonne le variabili oggetto di studio, e i valori sulla diagonale tutti pari ad 1 (in questo studio però noi non ci addentreremo). Ma soprattutto, questo tipo di analisi dei dati si applica in modo particolare alla fisica, dove è fondamentale scrivere leggi fisiche, anche empiriche, che legano tra di loro le diverse grandezze.

Un caso famoso è rappresentato dalla determinazione della dimensione frattale. « Delle grandezze, quella che ha una dimensione è la linea, quella che ne ha due è la superficie, quella che ne ha tre è corpo, e al di fuori di queste non si danno altre grandezze », diceva Aristotele 23 secoli e mezzo fa. Oggi dovrebbe ricredersi, dopo la scoperta dei frattali ad opera del matematico polacco naturalizzato francese Benoit Mandelbrot (1924-2010). Si dice frattale una struttura tale che una piccola parte di esso riproduce in scala ridotta la struttura intera; tale proprietà è detta di autosomiglianza, e caratterizza entità diversissime dell'universo, dalle galassie agli abeti, dai polmoni umani alla frequenza dell'uso delle parole in un quotidiano. Ad esempio, consideriamo i due Alberi di Valinor, Telperion e Laurelin, rispettivamente l'Albero d'Argento e l'Albero d'Oro che illuminavano la terra dei Valar nella notte dei tempi; ogni loro più piccola fronda riproduceva, in piccolo, la struttura dell'intero albero. Per spiegare tale inusuale proprietà, Mandelbrot generalizzò alcuni classici concetti matematici, tra i quali quello del numero di dimensioni di un corpo. Se esso viene calcolato per oggetti regolari (fogli, cilindri, sfere, ecc...), esso assume i consueti valori interi cui faceva riferimento Aristotele nel brano sopra riportato; ma, nel caso di una struttura come per esempio la forma delle coste dell'isola di Númenor, come le vedete nella mappa soprastante, ci si può rendere conto che non è così. Infatti essa possedeva un numero grandissimo di insenature e rientranze, il che rendeva molto difficile misurare l'effettiva lunghezza delle sue coste. Se le percorressimo in automobile, grazie al contachilometri avremmo una stima grossolana in km, ma se scendiamo dall'auto e osserviamo la forma precisa della linea di battigia misurandola con un metro a nastro, troveremo una lunghezza assai superiore. Ancora maggiore è il risultato andando a contare granello di sabbia per granello di sabbia, ottenendo una linea tortuosa la cui estensione totale appare veramente incredibile. Se ne conclude che la linea di costa di Númenor ha ben più dell'unica dimensione associatagli da Aristotele. Allo stesso modo, una superficie irregolare come quella di una spugna ha più di due sole dimensioni. Si potrà dunque parlare di 1,4 oppure di 2,7 dimensioni. Perciò, la differenza di natura tra diversi oggetti è ricondotta al calcolo della differenza tra le loro dimensioni.
Lo studio dei frattali ha ricevuto grande impulso negli ultimi decenni, perché solo mediante l'uso dei frattali è possibile generare e rendere visibili degli oggetti irregolari ed aleatori dotati di autosomiglianza, così come solo con simulazioni al calcolatore è possibile ricostruire paesaggi ed oggetti che non esistono a partire da questa basilare proprietà. Un modo molto semplice per calcolare la dimensione frattale usando materiale povero sfrutta della banale carta stagnola: si prendono dei fogli di alluminio da cucina, li si appallottola, se ne misura il diametro medio (si eseguono diverse misure con un calibro e poi se ne fa la media aritmetica), se ne determina la massa con una bilancia elettronica. Tra la massa M e il raggio medio r (la metà del diametro medio) intercorre una relazione del tipo:
dove α è la dimensione frattale. Nel caso di una sfera, la massa M è legata al raggio r attraverso la densità d dalla formula:
![]()
e quindi, essendo la densità e π due costanti, dal confronto tra le due precedenti si ricava α = 3 (infatti una sfera ha proprio tre dimensioni). Come determinare α sperimentalmente? Semplice: basta eseguire il logaritmo di entrambi i membri della (5). Per le proprietà dei logaritmi, si ha:
A questo punto, basterà determinare la retta di regressione tra i valori di ln M e ln r; il suo coefficiente angolare darà la dimensione frattale. Io ho preparato cinque palline di dimensioni diverse, ne ho misurato il raggio medio in millimetri e la massa in centigrammi, ed ho così ottenuto i seguenti valori:
|
pallina |
M |
r medio |
ln M |
ln r |
| #1 | 30 | 5,91 | 3,401 | 1,777 |
| #2 | 55 | 7,84 | 4,007 | 2,059 |
| #3 | 94 | 8,71 | 4,543 | 2,164 |
| #4 | 215 | 13,19 | 5,371 | 2,579 |
| #5 | 425 | 16,46 | 6,052 | 2,801 |
Il logaritmo di r sarà trattato come la variabile X, il logaritmo di M come la variabile Y. Vi consiglio di provare voi stessi a ripetere i calcoli da noi sopra svolti nel caso della Battaglia dei Campi del Pelennor, magari utilizzando un foglio elettronico. Il risultato che dovreste trovare è che ln r e ln M sono legati da una formula lineare di questo tipo:
ln M = 2,5578 x ln r – 1,1469
Il valore di ρ in questo caso vi risulterà pari a 0,9951, dunque la corrispondenza con un andamento lineare è davvero ottima. Confrontando questa con la formula (6) si ricava che α = 2,5578 è la dimensione frattale delle nostre palline di stagnola: più di una superficie (α = 2) ma meno di un solido (α = 3). L'analisi statistica descritta in questa lezione ci ha così permesso di dimostrare che delle semplici palline di carta stagnola non sono dei "solidi" come noi li intendiamo, bensì dei frattali!

Con questo riteniamo conclusa l'introduzione alla Fisica, e possiamo inoltrarci nel primo capitolo di essa, dedicato alla Cinematica del punto materiale. Per continuare con me questo affascinante viaggio attraverso l'universo di Tolkien, cliccate qui e passate alla pagina successiva.
![]()