![]()
|
« Lheben teil Brann i annon ar neledh neledhi gar godrebh » (Tolkien: Artista e Illustratore) |
La Fisica è un'indagine del mondo effettuata tramite gli strumenti della Matematica; questo la differenzia da altri tipi di indagine del mondo, ad esempio dalla filosofia. Oggetto della Fisica sono perciò degli oggetti dette grandezze fisiche, e grandezza fisica è ogni oggetto che può essere oggetto di misura. La misura è il confronto con un'unità di misura, e quindi richiede tre elementi:
un sistema di numerazione
un'unità di misura
uno strumento di misura
Cominciamo con il primo punto. La Grammatica Quenya elaborata da Tolkien contiene l'intero sistema numerico di questa lingua, incluse le istruzioni per realizzare multipli e frazioni di numero; ciò indica che gli Elfi avevano adottato un sistema matematico piuttosto avanzato. "Parma Eldalamberon" (in Quenya "il libro delle lingue elfiche"), la fanzine che pubblica il materiale lasciatoci da Tolkien riguardo le lingue da lui ideate, ha pubblicato una tabella dei numeri cardinali in lingua Quenya:
| 1 | er (un singolo), min (uno, primo) |
| 2 | satta (entrambi), yúyo (due) |
| 3 | nelde |
| 4 | kanta |
| 5 | lemin |
| 6 | enqe, enekse |
| 7 | otso |
| 8 | tolto |
| 9 | hue |
| 10 | kea, kai, kainen |
| 11 | minqe |
| 12 | yunqe |
| 13 | nelkea |
| 14 | kankea |
| 15 | lenkea, leminkea |
| 16 | enkea, enekkea |
| 17 | okkea |
| 18 | tolkea or hualqe |
| 19 | húkea |
| 20 | yukainen |
| 21 | min yukainen |
| 22 | yúyo yukainen |
| 30 | nel(de)kainen |
| 40 | kan(ta)kainen |
| 50 | leminkainen |
| 60 | enekkainen |
| 70 | otsokainen, okkainen |
| 80 | tol(to)kainen |
| 90 | huekainen |
| 100 | tuksa, keakai(li) |
| 110 | kea tuksa, minqekainen |
| 120 | yukainen tuksa, yunqekainen |
| 200 | yúyo tuksa, yutuksa |
| 300 | nelde tukse |
| 1000 | tuksakainen, tuksainen, húme |
| 2000 | yúyo húmi |
| 1 milione | mindóra |
| 2 millioni | yundóra |
| 3 millioni | neldóra |
| 4 millioni | kantóra |
| 5 millioni | lemindóra |
| 6 millioni | enqendóra |
| 7 millioni | otsondóra |
| 1 miliardo | yundóre |
| 1000 miliardi | neldóre |
| 1 milione di miliardi |
kantóre |
Il sistema qui mostrato è decimale, cioè a base 10. Cosa significa? Uomini, elfi, nani e hobbit hanno tutti in comune la circostanza di avere 10 dita, per cui è conveniente raggruppare i numeri in gruppi di 10 (nel nostro mondo, il primo a ricollegare questo sistema di numerazione al numero delle nostre dita fu Aristotele). Lo dimostra il fatto che, per numeri maggiori di 9, ritorna la radice "kainen", cioè 10. 11 e 12 terminano per "qe", e i numeri successivi sino a 19 terminano per "kea", evidente riferimento a "kainen". Ciò avviene anche in italiano, dove undici, dodici, tredici... contengono tutti la desinenza "-dici" che rimanda a dieci. Tredici in Quenya si dice "nelkea", ottenuto da "nelde" (tre) più "kea" (dieci), così come nei numeri romani XIII equivale a X + I + I + I = 10 + 1 + 1 + 1 = 13. "Yunqe" significa 12 ("due più dieci"), mentre 20 si dice "yukainen" ("due decine"), dunque la radice etimologica è la stessa, così come in inglese "twelve" (antico inglese "twelf") deriva da "two left" (due a sinistra del dieci, quindi 2 + 10) e "twenty (antico inglese "twentig") deriva da "two" + "tig" (gruppo di dieci).
Si noti che sistema decimale non significa necessariamente notazione posizionale. Questo fatto è talmente importante, che merita una spiegazione supplementare. I greci e i romani usavano una notazione additiva, cioè ogni simbolo ha sempre lo stesso valore numerico, che viene aggiunto o sottratto dagli altri valori a seconda della sua posizione all'interno del numero. Così, IX significa 9 perché I (1), essendo a sinistra di X (10), lo si sottrae, mentre XI significa 11 perché I si somma a X, trovandosi alla sua destra. Allo stesso modo CD significa 500 - 100 = 400, DCC = 500 + 100 + 100 = 700. Invece nella notazione posizionale ogni simbolo cambia valore numerico all'interno del numero a seconda della sua posizione; tali sono i sistemi di numerazione Maya e quello indiano (detto arabo perchè furono gli Arabi a veicolarlo in Europa nel Basso Medioevo). Così, nel numero 525, il primo 5 a destra ha precisamente il valore numerico di 5, mentre il 5 più sinistra ha il valore di 5 x 102 = 5 x 100 = 500. In pratica, la prima cifra a destra va moltiplicata per 1, la seconda per 10, la terza per 100 e così via, prima di eseguire la somma totale. Gli Elfi, che erano i depositari di tutta la conoscenza della Terra di Mezzo, potevano aver adottato questo tipo di notazione? Forse sì. Ecco infatti le cifre elfiche ideate da Tolkien a confronto con le rispettive cifre arabe:

Come si vede, esiste un simbolo per lo zero, il che sembra deporre a favore di una notazione di tipo posizionale (in quella additiva lo zero non avrebbe senso). Tuttavia, il 10 non è formato dai simboli "1" e "0" affiancati, ma per esso vi è un simbolo speciale. Inoltre "2" e "3" sono formati rispettivamente con due e con tre simboli "1", mentre "4" ha un simbolo apposito. "5" e "6" sono formati aggiungendo uno o due "1" a destra di "4", ma la regola non vale per il "7", che ha un simbolo speculare del "4". Anche "8" e "9" non sono costruiti con gli "1", ma con simboli ad hoc. Così "10" e "11". Invece, a sorpresa è 12 ad essere costruito come "0" + "1". Che cosa significa?
Il fatto è che, a dispetto della lista sopra riportata, nel sistema numerale elfico vi sono tracce di numerazioni non decimali. Tanto per cominciare, 18 oltre che "tolkea" si può anche esprimere come "hualqe", che è legato a "hue" (9) e quindi sembra voler dire "due volte 9": una traccia di notazione in base 9? Inoltre il fatto che "0" + "1" sia associato a 12 e non a 10 sembra indicare che, almeno agli inizi, il sistema di numerazione elfico fosse duodecimale, quindi a base 12, e non a base 10 come appare dai nomi dei numeri sopra riportati. Come funziona tale sistema?
Per comprenderlo, proviamo a scrivere il numero 3021 (numero degli anni della Terza Era di Arda secondo le appendici A, B e C del SdA) utilizzando questo sistema. Per questo, dovremo pensare in termini di potenze non di 10, ma di 12. Nel sistema decimale il numero considerato va così scomposto:
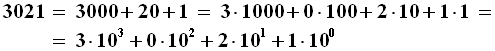
Le potenze di 12 da considerare sono 120 = 1, 121 = 12, 122 = 144 e 123 = 1728. 124 = 20736 non va considerata, perchè è maggiore del numero da noi preso in considerazione. 3021 è divisibile per 1728 solo una volta, perchè il doppio di 1728 è 3456, che è maggiore di 3021. Sottraendo 1728 da 3021 si ottiene 1293, che a sua volta andrà diviso per la potenza di 12 immediatamente inferiore, ovvero 144. 1293 diviso 144 ci dà 8 con il resto di 141, come chiunque può verificare con una calcolatrice tascabile. A sua volta 141 diviso 12 dà 11 con il resto di 9. Di conseguenza il nostro numero 3021 in notazione duodecimale potrà essere così riscritto:
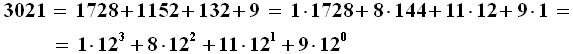
Ne consegue che 9 sarà la prima cifra a sinistra del nostro numero, 11 la seconda, 8 la terza e 1 la quarta. Sorge però un problema: 11 non è una cifra, e può essere confuso con due 1 affiancati. Ne consegue che i dieci simboli tradizionali del sistema decimale (0, 1, 2 3, 4, 5, 6, 7, 8, 9) non bastano, e ne dobbiamo aggiungere altri due, con il significato di 10 e 11. Non vale la pena di inventare simboli strani: usiamo la lettera A con il significato numerico di 10, e B con quello di 11! Ne consegue che le nostre cifre saranno dodici: 0, 1, 2 3, 4, 5, 6, 7, 8, 9, A, B. Il numero 3021 in notazione duodecimale verrà perciò scritto 18B9. Siccome si è detto che gli Elfi scrivevano le cifre in ordine inverso al nostro, cioè con la potenza di 12 minore a sinistra anziché a destra, scriveremo:
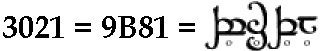
Il procedimento per trasformare un numero in notazione decimale (0-9) in uno in notazione duodecimale (0-B) è il seguente. Si prenda il 1973, anno della morte di J.R.R. Tolkien. Lo si divida per 12 e si trova 164, con resto di 5. Poi si divide 164 per 12, trovando 13 con il resto di 8. Infine si divide 13 per 12, ottenendo 1 con il resto di 1. Qui il calcolo si arresta. Ponendo i numeri trovati in ordine inverso, si trova 1185, che è l'equivalente duodecimale di 1973. L'operazione può essere sintetizzata come segue:

Al contrario, per trasformare un numero in notazione duodecimale (0-B) in uno in notazione decimale (0-9) occorre operare come segue. Sia il numero 7A2B; ognuna delle cifre andrà moltiplicata per una potenza di 12. La B a sinistra, che vale 11, andrà moltiplicata per 12 alla 0, cioè per 1; il 2 in seconda posizione andrà moltiplicato per 12 alla 1, cioè per 12; la A in terza posizione, che equivale a 10, andrà moltiplicata per 12 alla 2, cioè per 144; e il 7 in quarta posizione andrà moltiplicato per 12 alla 3, cioè per 1728. Il risultato è:
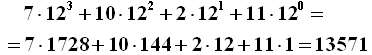
e quindi si passa in questo modo dal numero scritto in cifre elfiche a quello scritto in cifre arabe:
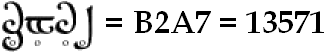
Come si vede, è un sistema particolarmente ingegnoso, che però sembra fare a pugni con l'elenco dei numeri Quenya che abbiamo riportato qui sopra. L'ipotesi è che Tolkien abbia inizialmente concepito la numerazione Quenya come un sistema decimale, analogo a quello usato nel nostro mondo, per poi passare gradualmente ad un sistema duodecimale, pur non sistematizzando mai tale numerazione in maniera definitiva.
Vi sono anche tabelle di numeri ordinali e di avverbi moltiplicativi in lingua Quenya:
| Primo | minya | Una volta | eru, eresse, ellume |
| Secondo | potsina, etya | Due volte | yullume |
| Terzo | nelya | Tre volte | neldellume |
| Quarto | kanya | Quattro volte | kantallume |
| Quinto | leminya | Cinque volte | lemillume |
| Sesto | enetya | Sei volte | enqellume |
| Settimo | otya | Sette volte | otsollume |
| Decimo | kaiya, keatya | Dieci volte | keallume |
| Ventesimo | yukainenya | Venti volte | yukainellume |
| Centesimo | tuksanya | Cento volte | tuksallume |
I numeri ordinali sono coniati a partire dai cardinali con le desinenze -ya, -tya e -nya; a parte "Eru", "l'Uno", uno dei nomi di Iluvatar, l'Essere Supremo, l'unica forma che sfugge a questa regola è "potsina", che significa "prossimo". Analogamente i moltiplicativi sono ottenuti con la desinenza -llume. Ciò ricorda da vicino il latino: quattuor è il cardinale (quattro), quartus l'ordinale (quarto), quater è il moltiplicativo (quattro volte); la radice è la stessa, cambiano le desinenze. L'utilizzo di queste forme è sintetizzato nella frase "yullume i hualqe", riportata in Parma Eldalamberon, che significa "due volte nove è diciotto": si tratta dell'unico esempio che io conosca di matematica elfica, anche se presumibilmente le conoscenze dei Primogeniti non si fermavano certo all'aritmetica.

Stabilito un sistema di numerazione, occorre stabilire un sistema di unità di misura. La sua necessità è evidente: fare in modo che, quando si offre una valutazione numerica di una grandezza attraverso il suddetto sistema di numerazione, essa abbia lo stesso significato per tutti. I sistemi di misura adottati dalla Fisica rappresentano l'evoluzione storica dei sistemi di pesi e misure sviluppati fin dai tempi remoti per scopi commerciali, e che hanno dato origine agli strumenti utilizzati da venditori e acquirenti per concordare in maniera univoca sulla quantità di merce trattata. Spiegherò questo concetto con un esempio. Supponiamo che un esponente della borghesia veneziana a fine settecento si rechi nello Stato di Milano a comprare "cinque braccia di stoffa" per realizzare dei vestiti. Tornato nella Serenissima Repubblica, il mercante si accorge che la stoffa da lui comprata è insufficiente per realizzare gli abiti desiderati. Deve prendersela con il mercante milanese, che presumibilmente lo ha truffato? Oppure deve cercare se ha commesso un errore nei calcoli? Nulla di tutto questo. Il fatto è che il "braccio da lana" a Venezia misurava 68,3 cm, mentre a Milano misurava 59,5 cm. Ne consegue che con "cinque braccia" il veneziano intendeva 3,415 metri di stoffa, mentre la stessa espressione a Milano equivaleva solo a 2,975 metri. E, se questo esempio non basta, aggiungerò che praticamente ogni città d'Italia aveva un "braccio" di lunghezza differente: 59,9 cm a Torino, 67,9 cm a Bergamo, 54,0 cm a Parma, 64,0 cm a Bologna, 58,3 cm a Firenze, 66,1 cm a Napoli; a Verona addirittura c'erano due diverse unità di misura, il "brassio longo" di 64,8 cm e il "brassio corto" di 64,2 cm. Appare evidente che, in un simile Far West di unità di misura, elaborare una "fisica" come noi la conosciamo è semplicemente impossibile. La ricerca scientifica è infatti basata sulla collaborazione tra cervelli che lavorano in laboratori spesso molto distanti tra loro, e l'uniformità tra unità di misura è condizione necessaria per portare avanti questo lavoro in staff.
Per questo venne ideato il Sistema Internazionale di Unità di Misura, noto più semplicemente con la sigla S.I., evoluzione di quello che in origine era chiamato Sistema Metrico Decimale. Un sistema di unità di misura di tipo decimale venne concepito per la prima volta da Simon Stevin (1548-1620) e John Wilkins (1614-1672), primo Segretario della Royal Society, ma venne realizzato solo durante la Rivoluzione Francese, che abrogò l'antico diritto feudale di stabilire pesi e misure in ogni località. Il 13 luglio 1790 Thomas Jefferson (1743-1826), uno dei fondatori e successivamente terzo Presidente degli Stati Uniti d'America, presentò al Congresso un documento intitolato "Piano per stabilire l'uniformità nella monetazione, nei pesi e nelle misure degli Stati Uniti" (sembrerà ironico, ma tuttora gli USA sono uno dei tre paesi del mondo in cui il Sistema internazionale non è stato adottato come unico o principale sistema di misurazione; gli altri due sono la Liberia e la Birmania). Dietro proposta dell'ex vescovo (e "uomo per tutte le stagioni") Charles Maurice de Talleyrand-Périgord (1754-1838), l'Assemblea Nazionale Francese istituì una commissione sotto l'egida dell'Académie des Sciences per realizzare l'unificazione di pesi e misure, commissione costituita da cinque tra i migliori scienziati dell'epoca: Jean-Charles de Borda (1733-1799), ideatore di tavole di logaritmi; Joseph-Louis Lagrange (1736-1813), nato a Torino, fondatore della meccanica moderna; Pierre-Simon de Laplace (1749-1827), insigne matematico ed astronomo; Gaspard Monge, Conte di Péluse (1746-1818), ideatore della geometria descrittiva; e Nicolas de Caritat, marchese di Condorcet (1743-1794), membro del gruppo dell'"Enciclopedia" e tra i fondatori dell'analisi matematica, che successivamente sarebbe morto in un carcere rivoluzionario. La commissione discusse proprio l'uso del sistema duodecimale come alternativa al sistema decimale: un'incredibile coincidenza con quanto detto sopra a proposito del possibile sistema di numerazione elfico! Alla fine però la commissione decise che i vantaggi della divisibilità per tre e quattro sarebbero stati controbilanciati dalle complicazioni implicite nell'introduzione di un sistema affatto nuovo, e il 27 ottobre 1790 si pronunciò definitivamente per il sistema decimale. Il 19 giugno 1791, il giorno prima che Luigi XVI tentasse la fuga dalla Francia venendo arrestato a Varennes, il re accettò di finanziare la misura del meridiano terrestre, necessaria per stabilire un'unità di misura valida per tutti. Di tale misura si incaricarono gli scienziati Jean-Baptiste Delaimbre (1749-1822) e Pierre Méchain (1744-1804). Durante le convulse fasi della storia francese che portarono il 21 gennaio 1793 all'esecuzione di Luigi XVI e al Terrore rivoluzionario, la riforma dei pesi e delle misure e in particolare la misurazione del meridiano terrestre proseguì come se niente fosse, e il 11 luglio 1792 la Commissione propose formalmente i nomi "metro" e "litro" e i prefissi "kilo", "etto", eccetera. Fa un po' impressione pensare a quei due impavidi scienziati che continuavano a triangolare il suolo francese per misurare il meridiano tra Barcellona e Dunkerque mentre la ghigliottina lavorava a tutto spiano, ma questa è la situazione nella quale nacque il Sistema Metrico Decimale. Il 15 novembre 1798 Delaimbre e Méchain completarono ufficialmente la misura dell'arco di meridiano tra Dunkerque e Barcellona, e proposero l'introduzione di un'unità di misura della lunghezza chiamata metro, dal greco "misura", definita come la quarantamilionesima parte del meridiano terrestre; di essa fu realizzato un prototipo in platino-iridio, oggi conservato al Bureau International des Poids et Mesures a Sèvres, presso Parigi. Contemporaneamente fu fabbricato anche un chilogrammo campione, pari alla massa di un decimetro cubo di acqua a 4° C. Il primo nome proposto per tale unità era "grave", ma si trovò che somigliava troppo a "Graf", in tedesco "Conte", titolo nobiliare inaccettabile per la Francia rivoluzionaria, e siccome era già stato definito un "grammo" troppo piccolo per essere adottato, l'unità fondamentale delle masse fu definita "chilogrammo". Ecco perchè l'unità di massa è l'unica a contenere il prefisso "chilo".
L'Assemblea Nazionale portò il tutto alle estreme conseguenze, e si pronunciò a favore della decimalizzazione anche delle misure di tempo e degli angoli! Con il decreto del 5 ottobre 1793 venne introdotto in Francia il Calendario Repubblicano, che decimalizzava tutte le misure temporali: il giorno fu suddiviso in 10 "ore decimali", un '"ora decimale" in 100 "minuti decimali" e un "minuto decimale" in 100 "secondi decimali". L'"ora decimale" corrispondeva a 2 ore 24 minuti, il "minuto decimale" a 1 minuto e 26 secondi, e il "secondo decimale" a 0,864 secondi. La "settimana rivoluzionaria" fu divisa in 10 giorni, e ogni mese (i mesi dell'anno erano comunque dodici, con i nomi cambiati) era composto da tre "settimane". Ogni anno aveva anche cinque o sei giorni supplementari per arrivare a un totale di 365 o 366 giorni. L'angolo giro fu diviso invece in 400 gradi centesimali, in modo che ogni angolo retto fosse formato da 100 gradi centesimali, ed ogni grado era diviso in 100 centesimi. Quest'ultimo tipo di misurazione degli angoli è tuttora riportato dalle moderne calcolatrici digitali, che prevedono tre modalità di misurazione degli angoli: RAD, cioè radianti; DEG, cioè gradi sessagesimali; e GRAD, cioè gradi centesimali. In effetti, però, oggi le misure decimali di tempo ed angoli non sono più utilizzate da nessuno. Il calendario rivoluzionario venne soppresso da Napoleone con un decreto del 9 settembre 1805; nel 1871, durante la Comune di Parigi, fu riutilizzato a partire dal 5 maggio, ma nuovamente soppresso al termine di quest'altra esperienza giacobina.

Unità di misura a confronto: il
doppio braccio, antica misura
toscana, e il metro nel portico del Palazzo Comunale di Pistoia
Il secondo sessagesimale, che nonostante i tentativi rivoluzionari è oggi l'unità fondamentale di ogni misura temporale, fu inizialmente definito come 1/86.400 del giorno solare medio. Tuttavia si scoprì ben presto che la durata del giorno va lentamente ed impercettibilmente allungandosi, a causa di vari fattori, ma principalmente dell'interazione gravitazionale tra Terra e Luna e delle forze di marea che quest'ultima esercita sul nostro pianeta. Ne consegue che oggi un secondo è lievemente inferiore ad 1/86.400 del giorno solare medio. Preso atto di questo fenomeno che rendeva impossibile una definizione univoca di secondo, nel 1956 il Bureau international des Poids et Mesures ridefinì il secondo in termini di rivoluzione terrestre come 1/31.556.925,9747 dell'anno tropico il 1 gennaio 1900 alle ore 12. Questa definizione, più complicata della precedente (fa riferimento al tempo effemeride, cioè quello determinato dalla posizione dei corpi celesti) venne ratificata dall'undicesima Conferenza Generale sui Pesi e Misure del 1960, ma partì la "caccia" ad una definizione più semplice e riproducibile. Ci riuscirono Louis Essen (1908-1997) del National Physical Laboratory di Teddington (Inghilterra) e William Markowitz (1907-1998) dello United States Naval Observatory di Washington, i quali determinarono con estrema precisione la frequenza dell'isotopo di cesio-133. Come risultato, nel 1967 la tredicesima Conferenza Generale sui Pesi e Misure definì il secondo come la durata di 9.192.631.770 periodi della radiazione corrispondente alla transizione tra due livelli energetici dello stato fondamentale dell'atomo di cesio-133. In parole povere, un elettrone può saltare da un orbitale ad un altro ad energia maggiore, ma poi ritorna al suo posto ed irraggia sotto forma di radiazione elettromagnetica la differenza di energia tra i due livelli. Questa è la definizione di secondo tuttora adottata. Anzi, il secondo è l'unità di misura definita con maggiore accuratezza, dell'ordine di 10–12!
Metro, chilogrammo e secondo sono tre delle unità fondamentali di quello che nel 1889 la prima Conferenza Generale sui Pesi e Misure ribattezzò "Sistema MKS" dal nome delle tre unità suddette, ma oggi esse non sono le uniche. Nel 1946, su proposta del fisico italiano Giovanni Giorgi (1871-1950), il sistema fu denominato "Sistema MKSA" e adottato dalla Commissione Elettrotecnica Internazionale, introducendo l'Ampére come quarta unità di misura fondamentale, per poter includere anche le grandezze caratteristiche dell'elettrologia e del magnetismo; il Sistema MKSA fu chiamato anche "Sistema Giorgi" in onore del suo ideatore. Nel 1954 la decima Conferenza Generale sui Pesi e Misure aggiunse il kelvin e la candela come unità di misura fondamentali, così da includere nel Sistema Giorgi anche le grandezze caratteristiche della termodinamica e dell'ottica. Nel 1961 l'undicesima Conferenza Generale sui Pesi e Misure ridefinì il MKSA con il nome di Sistema internazionale o S.I. Nel 1971 la quattordicesima Conferenza Generale sui Pesi e Misure aggiunse la mole, il radiante e lo steradiante fra le unità fondamentali. Nel 1995, infine, la ventesima Conferenza Generale dei Pesi e Misure ha declassato radiante e steradiante ad unità derivate. Ecco tutte e sette le unità fondamentali, riunite in un'unica tabella:
| Grandezza | Unità | Simbolo |
| Lunghezza | metro | m |
| Massa | chilogrammo | Kg |
| tempo | secondo | s |
| corrente elettrica | Ampére | A |
| temperatura | kelvin | K |
| intensità luminosa | candela | cd |
| quantità di materia | mole | mol |
Tutte le altre unità di misura delle grandezze fisiche sono derivate da queste sette. Ad esempio, l'unità S.I. della forza, il Newton, è definita come la forza che imprime alla massa di un chilogrammo l'accelerazione di un metro al secondo quadrato. Ne consegue che 1 N = 1 m Kg s–2; il nome "Newton" è stato assegnato per motivi di brevità nella nomenclatura. Basti pensare che l'unità di misura nel S.I. dell'induttanza (il rapporto tra il flusso magnetico del campo concatenato ad un circuito e la corrente che fluisce in esso) è il metro quadrato per chilogrammo fratto secondo quadrato per Ampére al quadrato (m2 kg s−2 A−2); appare necessario assegnare per brevità un nome a questa complicata unità, che è chiamata Henry in onore del fisico statunitense Joseph Henry (1797-1878), noto per essere l'inventore del campanello elettrico. In Italia il S.I. è il sistema di misura che deve essere obbligatoriamente adoperato a partire dal DPR numero 802 del 12 agosto 1982, ai sensi della Direttiva del Consiglio CEE del 18 ottobre 1971, modificata il 27 luglio 1976. Il suo uso è obbligatorio nella stesura di atti e documenti con valore legale, altrimenti gli atti stessi potrebbero essere invalidati.

"Tolkien: Artista e Illustratore" è una raccolta di dipinti (per lo più ad acquerello) e disegni di J.R.R. Tolkien realizzati per i suoi racconti, curata da Wayne G. Hammond e Christina Scull e pubblicata postuma nel 1995. Quest'opera dimostra che Tolkien era un artista non solo con le parole, ma anche per immagini, e ha suscitato l'ammirazione di molti lettori. La raccolta comprende le illustrazioni realizzate da Tolkien per i suoi figli, in particolare nelle sue "Lettere a Babbo Natale" e in "Mr. Bliss". A noi l'opera interessa perché sulla mappa di Thrór in essa contenuta è leggibile una frase in lingua Noldorin (una delle tante ideate dal nostro autore) che ben si accorda con le misure di cui abbiamo parlato sopra:
«
Lheben teil Brann i annon ar neledh neledhi gar godrebh »
(trad. letterale: la porta è alta cinque piedi e in tre possono camminare affiancati)
Al di là di tutte le considerazioni linguistiche che si potrebbero fare circa l'utilizzo di numeri cardinali in Noldorin, la parola lheben ("cinque") è qui usata per misurare l'altezza di una porta in unità dette "piedi" (teil). L'uso di quest'unità cosiddette antropometriche, perchè basate sulle dimensioni del corpo umano, non deve certo stupire, poiché esse furono le prime unità di misura anche nel nostro universo. Il piede fu certamente una delle più antiche, e veniva utilizzato dall'antica Grecia fino alla Scozia. Presso i Romani, questa misura equivaleva a 29,64 cm. In Italia variava moltissimo da una regione all'altra, così come il braccio sopra ricordato: a Milano misurava 43,52 cm, a Roma 29,79 cm; a Parigi era in uso un piede da 32,48 cm, a Vienna uno da 31,61 cm. Oggi il piede internazionale (o "International foot") vale 30,48 cm, ed è usatissimo nei paesi anglosassoni, soprattutto per misurare le altezze e le profondità (dire che un aereo vola a "trentamila piedi" equivale ad affermare che vola circa a 9150 m di quota). Il piede equivale a 12 pollici. Anche il pollice è un'unità antichissima: la più antica citazione del suo uso in Inghilterra è contenuta nelle "Leggi di Etelberto", che risalgono addirittura al sesto secolo. Oggi esso equivale a 2,54 cm, ed è usato anche al di fuori del mondo anglosassone per misurare la diagonale degli schermi di televisori e computer, ma anche i tubi idraulici e i cerchioni per auto e moto. Nell'antichità invece l'unità più diffusa era il cubito, inteso come la lunghezza dell'avambraccio dal gomito fino alla punta del dito medio. Equivaleva a circa mezzo metro, ma ovviamente variava moltissimo da regione a regione. In Egitto il Cubito Reale (niswt) equivaleva a 52,3 cm (ne sono stati trovati precisi campioni nelle tombe sulle rive del Nilo), era suddiviso in 7 palmi (schesep) e 28 dita (djeb'a); uno dei suoi multipli era la canna (khet), pari a 100 cubiti cioè a 52,3 metri. Ad Atene il cubito era detto pichis (in greco πήχης, "avambraccio"), secondo la mitologia era basato sull'avambraccio del mitico eroe Eracle e misurava 52,5 cm. A Roma misurava 44,44 cm e in Inghilterra 45,72 cm, corrispondendo a un piede e mezzo. Il cubito è anche l'unità di misura principale citata dalla Bibbia: nell'Antico Testamento è citato ben 273 volte, e si pensa che misurasse 44,45 cm, anche se non c'è accordo tra gli esegeti. Ad esempio è in cubiti che YHWH comunica a Noè le dimensioni dell'Arca di Noè:
« Ecco come devi farla: l'arca avrà trecento cubiti di lunghezza, cinquanta di larghezza e trenta di altezza. » (Genesi 6, 15)
Se il cubito ha la misura sopra precisata, l'arca di Noè era un cassone di 133,35 x 22,22 x 13,33 metri. Secondo alcuni tuttavia quella misura è data in cubiti babilonesi, poiché la redazione definitiva del Pentateuco fu eseguita durante l'esilio a Babilonia, e siccome un cubito babilonese misurava 46,87 cm, l'arca verrebbe a misurare 140,61 x 23,43 x 14,06 metri. Anche le misure dell'Arca dell'Alleanza e del Tempio di Salomone sono espresse in cubiti, ad esempio:
« Faranno dunque un'arca di legno di acacia: avrà due cubiti e mezzo di lunghezza, un cubito e mezzo di larghezza, un cubito e mezzo di altezza. » (Esodo 25, 10)
In cubiti ebraici, ciò equivale a 1,111 x 0,667 x 0,667 m. Anche la statura del proverbiale gigante Golia è misurata in quest'unità:
« Dall'accampamento dei Filistei uscì un campione, chiamato Golia, di Gat; era alto sei cubiti e un palmo » (1 Samuele 17, 4)
Il cubito ebraico era diviso in 6 tefachim o palmi, per cui l'altezza del colosso sarebbe stata di 2,89 metri!

| Il campione di cubito in legno dorato (sopra) che fu ritrovato nella tomba dell'architetto egizio Kha (XIV secolo a.C.), oggi al Museo Egizio di Torino, a confronto (sotto) con il metro campione di platino-iridio conservato al Bureau International des Poids et Mesures a Sèvres, vicino a Parigi (sono visibili anche il litro e il chilogrammo campione) |
E nell'universo di Tolkien? Per quanto possa sembrare strano, in esso la metrologia è delineata in maniera tutt'altro che superficiale. Infatti nell'appendice a "Il disastro dei Campi iridati", la novella nell'ambito dei "Racconti incompiuti" che contiene la cronaca della battaglia in cui Isildur morì e l'Unico Anello fu smarrito, troviamo un elenco delle misure lineari utilizzate dai Dúnedain, gli abitanti di Númenor. Quello che segue è un riassunto realizzato dal mio amico e mentore Edoardo Secco.
L'unità númenoreana fondamentale, equivalente al nostro metro, era il ranga. 5000 rangar equivalevano a un lár; Tolkien dice che un lár equivaleva a una lega, più o meno tre miglia terrestri, ossia 4826 metri. Il ranga quindi dovrebbe misurare 96,52 cm. Secondo il nostro Professore, prima della "standardizzazione" le unità di misura erano antropometriche, come i piedi, i pollici e i cubiti del nostro universo. Ranga infatti in Quenya significa "passo", e come lunghezza « è indicato spesso come la lunghezza del passo, dal calcagno all'alluce di un uomo adulto che cammina velocemente ma senza forzare. » Invece lár significa « "pausa" perché, eccezion fatta nel caso di marce forzate, dopo aver coperto questa distanza si faceva una breve pausa. »
Tolkien non nomina unità di superficie e di volume, ma non è difficile immaginare che l'unità di misura delle aree fosse il ranga quadro, pari a 0,9316 m², e che quella dei volumi fosse il ranga cubo, equivalente a 0,8992 m³) del volume; quale nome esatto dessero i Númenoreani a tale unità, però, lo ignoriamo. Dalle nostre parti, un metro cubo d'acqua ha una massa di 1000 chilogrammi; se lo stesso standard era adoperato sull'Isola dei Re, l'unità númenoreana di massa corrispondeva alla massa di un millesimo di ranga cubo d'acqua, cioè a 0,8974 dei nostri chilogrammi.
E veniamo alla cronometria, cioè alla misura del tempo. L'Appendice D del "Signore degli Anelli" è interamente dedicata ai calendari. In essa Tolkien dice che l'anno durava quanto il nostro: 365 giorni, 5 ore, 48 minuti, 46 secondi. Questa, equivalente per l'esattezza a 365,2422 giorni, è la durata dell'anno tropico (dal greco tropos, "rotazione"), pari al tempo che intercorre fra due passaggi successivi del Sole allo zenit di uno stesso tropico, cioè fra due solstizi od equinozi dello stesso nome. Sull'anno tropico è fondato il calendario gregoriano, da noi adottato, che fu istituito nel 1582 da Papa Gregorio XIII (1572-1585) con la bolla " Inter Gravissimas". L'anno tropico non va confuso con l'anno siderale, pari al tempo che impiega il Sole a ritornare nella stessa posizione rispetto alle stelle della sfera celeste. Quest'ultimo è pari a 365 giorni, 6 ore, 9 minuti e 10 secondi (365,2564 giorni), ed è di 20 minuti e 24 secondi più lungo dell'anno tropico, a causa del moto di precessione dell'asse terrestre.
Mentre sappiamo molto circa i calendari, non sappiamo di preciso come venisse suddiviso il tempo giornaliero. Nel capitolo IV del libro quinto del "Signore degli Anelli", intitolato "L'assedio di Gondor", si dice che la campana di Minas Tirith batteva le ore, ma ignoriamo quanto durassero e se fossero ulteriormente suddivise; ne "Lo Hobbit" le ore vengono indicate come se fossero del tutto uguali a quelle in uso nel nostro universo. In lingua Quenya le principali unità di misura del tempo sono "aurë" (giorno), "asta" (mese), "loa" (anno); "yén " significa "anno lungo" (l'equivalente elfico del secolo, un ciclo di 144 anni solari), e "randa " significa "età", cioè le ere del mondo. Quanto alle stagioni, "coirë" indicava l'inizio della primavera, "tuilë" la seconda parte di essa, " lairë" l'estate, "yávië" l'inizio dell'autunno, "quellë" la fine dell'autunno (anche "lasselanta", "la caduta delle foglie") e "hrívë" l'inverno. I mesi invece sono "Narvinyë" (gennaio), "Nénimë" (febbraio), "Súlimë" (marzo), "Víressë" (aprile), "Lótessë" (maggio), "Nárië" (giugno), "Cermië" (luglio), "Úrimë" (agosto), "Yavannië" (settembre), "Narquelië" (ottobre), "Hísimë" (novembre), "Ringarë" (dicembre). In Sindarin invece "arad" significa "giorno", "idhrin" sta per "anno", "anrand" per "era"; le stagioni sono "echuir" (l'inizio della primavera), "ethuil" (la fine della primavera), " laer" (estate), "iavas" (l'inizio dell'autunno), "firith" (la fine dell'autunno) "rhîw" (l'inverno). Infine, i mesi sono "Narwain " (gennaio), "Nínui " (febbraio), "Gwaeron " (marzo), "Gwirith " (aprile), "Lothron " (maggio), "Nórui " (giugno), "Cerveth " (luglio), "Urui " (agosto), "Ivanneth " (settembre), "Narbeleth " (ottobre), "Hithui " (novembre) e "Girithron " (dicembre).
Come si è visto, il Sistema Internazionale di misura comprende anche unità di misura fondamentali della corrente elettrica, della temperatura, dell'intensità luminosa e della quantità di materia. I Númenoreani (come gli abitanti di Atlantide nelle leggende della nostra realtà) possedevano conoscenze scientifiche molto avanzate, quindi è possibile che disponessero di scale termometriche, di una fotometria e di una chimica, ma di esse nulla sappiamo. Difficilmente però essi padroneggiavano anche la corrente elettrica; dunque, probabilmente nel mondo di Tolkien l'Ampére non ha alcun corrispondente.

Prima di cambiare argomento, vediamo un esempio di misura nella Terra di Mezzo. Lo spunto è questo spettacolare grafico che ho trovato nel mare magnum del Web:

La Torre Oscura di Barad-dûr a confronto con alcuni tra i maggiori grattacieli del pianeta
Esso mostra un impietoso confronto tra la Torre Oscura di Barad-dûr, residenza di Sauron posta nel cuore della Terra di Mordor, e i più alti edifici esistenti nel nostro universo. L’umanità, fin da quando ha dato vita a civiltà monumentali, ha sempre cercato di spingersi verso il cielo, ritenuta la magione degli déi. Nacquero così le piramidi egizie, le ziggurat babilonesi, i templi Maya, fino ai campanili delle cattedrali gotiche e ai minareti delle moschee. Ma le moderne torri destinate a scalare il firmamento, non più per sfidare Dio come la Torre di Babele ma per mostrare la potenza economica delle grandi multinazionali devote al dio dollaro, sono i grandi grattacieli che adornano le nostre megalopoli così come le città medievali si adornavano di torri merlate. Grazie alle nuove tecniche costruttive basate sull'acciaio e sul vetro, sono diventati giganti sempre più smisurati, perdendo le sembianze di palazzi e abitazioni per assumere quelle di vere e proprie guglie puntate verso lo spazio.
Nel 2014 il grattacielo più alto del pianeta nel nostro universo è il Burj Khalifa ("Torre Khalifa") di Dubai, che tocca gli 828 metri per un totale di 160 piani. La sua costruzione è iniziata il 21 settembre 2004; la struttura esterna è stata completata il 1 ottobre 2009, ed è stato ufficialmente aperto al pubblico il 4 gennaio 2010. Esso ospita uffici, hotel, piscine e più di 700 appartamenti, ed è intitolata allo sceicco Khalifa bin Zayed Al Nahayan, emiro di Abu Dhabi e presidente degli Emirati Arabi Uniti. In precedenza l'edificio più alto al mondo era l'antenna radio di Varsavia, a Konstantynow, un sobborgo di Gąbin, alta 646,38 metri. Terminata il 18 maggio 1974, crollò a causa di un cedimento strutturale l'8 agosto 1991. Invece il secondo grattacielo più alto è la Shanghai Tower, tuttora in costruzione nel quartiere Pudong di Shanghai. Quando sarà completato, sarà alto almeno 632 metri per un totale di 128 piani. Al terzo posto si colloca la torre più alta dell'Al-Bait Abraj Towers, complesso edilizio situato alla Mecca, in Arabia Saudita; essa tocca i 601 metri e rappresenta la più alta torre con orologio esistente al mondo (oltre al più grande orologio da facciata). Solo quarto in questa speciale classifica di colossi si piazza il massimo edificio del Nord America, l'One World Trade Center di New York, che sorge sul sito delle Twin Towers del World Trade Center, abbattute l'11 settembre 2001 nel corso del peggior attentato terroristico della storia dell'uomo. Non ancora inaugurata, la torre maggiore del complesso è alta 1776 piedi, cioè 541,33 metri per 82 piani, in onore dell'anno della dichiarazione di indipendenza degli Stati Uniti (1776). Il più alto grattacielo d'Europa, la Shard London Bridge detta anche "la Scheggia", progettata da Renzo Piano ed inaugurata il 5 luglio 2012, è alta "solo" 310 metri per 87 piani di cui 72 abitabili, e si piazza solo al quarantacinquesimo posto della nostra classifica. In confronto il maggior edificio italiano, la Torre Unicredit di Milano, inaugurata l'11 febbraio 2014, con i suoi 231 metri di altezza per 32 piani più una guglia di 85 metri, è quasi un nanerottolo in confronto a quei giganti!
Se però la penisola arabica, la Cina e gli Stati Uniti vantano una sfilata impressionante di giganti d'acciaio, certamente non hanno fatto i conti con il reame di Mordor, che può vantare la torre più alta mai progettata, e cioè proprio Barad-dûr (in Sindarin "torre oscura", Lugbúrz nel linguaggio nero). La sua costruzione, iniziata nell'anno 1000 della Seconda Era, richiese oltre seicento anni, più quindi di ogni edificio del nostro universo, ed essa divenne la più grande fortezza mai edificata dopo Angband, la leggendaria dimora di Morgoth nella Prima Era. Ecco come la vede Frodo, quando la contempla dall'Amon Hen, dopo essere fuggito dal resto della Compagnia perchè Boromir ha tentato di sottrargli l'anello:
«
Frodo sedeva sul Seggio della Vista, ad Amon Hen, il Colle dell'Occhio degli
Uomini di Numenor [...] Lo sguardo dell'Hobbit fu irresistibilmente attratto
verso oriente; [...] spaziò su Gorgoroth, la Valle del Terrore nel Paese di
Mordor, ove sotto i raggi del Sole tutto era immerso nell'oscurità [...] Infine il suo sguardo si arrestò: muraglie e muraglie, cinte e bastioni, nera, incommensurabilmente forte, montagna di ferro, cancello d'acciaio, torre d'adamante, egli la vide:
Barad-dûr, la Fortezza di Sauron. Ogni speranza morì in lui. »
(SdA, libro II, cap. X)
Quanto sia alta la Torre Oscura, Tolkien non lo dice esplicitamente, ma è possibile eseguirne una stima nel modo seguente. Nella celebre trilogia cinematografica di Peter Jackson, Barad-dûr è chiaramente visibile dal Cancello Nero di Mordor, nonostante le tenebre perenni che avvolgono il regno di Sauron. Ora, nelle mappe della Terra di Mezzo i Cancelli del Morannon distano dalla Torre 100 miglia, equivalenti a 160 km (un miglio inglese o "statute mile" equivale a 1.609,344 metri). Quale dev'essere dunque l'altezza di una torre, per essere visibile da 160 km di distanza? Eseguiremo i calcoli usando il raggio terrestre medio, che misura 6373 km. Osserviamo la figura qui sotto:

La Torre Oscura (posta in A) risulta visibile dal Morannon (che si trova in B) se la tangente alla circonferenza terrestre nel punto B lambisce in C la sommità della paurosa dimora di Sauron, considerando che la luce si propaga in linea retta. L'arco AB misura come detto 160 km; considerando una circonferenza terrestre di 40.000 km, per trovare quanto vale il corrispondente angolo al centro AÔB = α basta una proporzione:
![]()
Il risultato è α = 1,44 gradi di meridiano. Ora, OBC è un triangolo rettangolo; le regole della trigonometria ci dicono che:
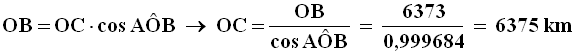
Infine, l'altezza AC della torre si ricava sottraendo OA da OC: sono ben 2000 metri! Questo ingegnoso metodo ci ha permesso di stimare l'altezza del quartier generale di Sauron, ma di solito questa stima viene abbassata, perchè (ovviamente) una tale altezza sembra davvero esagerata per qualsiasi costruzione effettuata da mani d'uomo, senza cemento armato né strutture in acciaio, ma anche per un altro motivo. Il famoso "Atlante della Terra di Mezzo" di Karen Wynn Fonstad (1945-2005), pubblicato a Boston nel 1981, riporta per il Monte Fato, il supervulcano che rischiarava la cupa terra di Mordor con le sue violente eruzioni, e che sorgeva non lontano dalla Torre Oscura, un'altezza di 4500 piedi, cioè di circa 1400 metri. Ora, poiché non appare credibile che la fortezza fosse più alta dell'Orodruin, anche a Barad-dûr viene attribuita un'altezza di circa 1400 metri, come nell'immagine soprastante. Si tratta comunque di un'altezza davvero ragguardevole: equivale a ben 275 piani, e rappresenta il 170 % dell'altezza del Burj Khalifa, il 220 % della Shanghai Tower e il 259 % dell'One World Trade Center, oltre a quasi cinque volte l'altezza della Tour Eiffel di Parigi e oltre dieci volte l'altezza della grande Piramide di Cheope a Gizah!
Potrà mai sorgere nel nostro universo una costruzione in grado di rivaleggiare con il pinnacolo che domina la buia terra di Mordor? I nuovi materiali e l’evoluzione dell’ingegneria edile ci consentono oggi di raggiungere altezze solo fino a qualche anno fa inimmaginabili. Grazie all’uso di materiali sempre più moderni e sempre meno costosi, come il cemento ad alta resistenza, le moderne cattedrali dell'alta finanza si arrampicheranno sempre più verso il firmamento, inerpicandosi verso l'alto alla ricerca di quello spazio che sempre più scarseggia nelle megalopoli del terzo millennio. L'Arabia Saudita ha messo in progetto di edificare a Jeddah la "Kingdom Tower", mentre il Kuwait è stato proposto di edificare la "Burj Mubarak Al-Kabir", entrambe destinate a superare la soglia psicologica dei 1.000 metri. Pare che questi progetti un po' visionari siano stati messi in naftalina a causa dell'imperversare della crisi economica, ma a Jeddah giurano che la "Kingdom Tower" sarà pronta per il 2018 e conterà 159 piani. E c'è qualcuno che si è spinto a proporre una vertiginosa "Mile Tower" alta esattamente un miglio, cioè 1609 metri per addirittura 500 piani. Se mai verrà realizzata davvero, questa fantascientifica torre simile a una freccia piantata nel cielo supererà la vertiginosa magione oscura di Sauron, e si potrà davvero affermare che la realtà ha superato la fantasia!
L'introduzione alla Fisica però non comprende solo i sistemi di numerazione e di misura, ma anche l'analisi statistica dei risultati sperimentali. Per questo, prima di avventurarci nella Cinematica, ho deciso di dedicare un capitolo proprio alla Statistica e alle sue applicazioni, fondamentali per qualsiasi scienza esatta. Chi vuole saperne di più, clicchi qui e passi alla lezione seguente!
![]()