La latitudine di Gran Burrone

Frodo non percepiva suoni, ma solo luminose immagini animate. Il mondo pareva rimpicciolito e muto...

(SdA, libro II, cap. X)

Rileggiamo insieme un brano del capitolo X del SdA, al quale ci siamo già riferiti nella nostra prima lezione, quando abbiamo cercato di valutare insieme l'altezza della Torre Oscura di Barad-dûr. Frodo ha resistito al tentativo di Boromir di farsi consegnare l'Unico Anello ed è fuggito, protetto dallo schermo di invisibilità che esso gli assicura, correndo su per il colle di Amon Hen. Frodo va a sedersi proprio sul trono di pietra eretto dai signori di Númenor, senza sapere che esso permette magicamente, a coloro che vi si siedono, di spingere lontano lo sguardo per centinaia e centinaia di chilometri.:

« [Frodo] non percepiva suoni, ma solo luminose immagini animate. Il mondo pareva rimpicciolito e muto. Egli sedeva sul Seggio della Vista, ad Amon Hen, il Colle dell'Occhio defgli Uomini di Númenor. Ad est lo sguardo spaziava su vaste terre inviolate, su pianure senza nome e foreste inesplorate. Guardò a nord, e vide il Grande Fiume serpeggiare ai suoi piedi come un nastro, e le Montagne Nebbiose piccole e dure parevano denti rotti. Guardò ad ovest, e vide gli immensi pascoli di Rohan; ed anche Orthanc, il pinnacolo d'Isengard, simile a una spina nera. Guardò a sud, e sotto di lui il Grande Fiume si gonfiava come un'onda che ta per infrangersi, e piombava giù dalle cascate di Rauros in un pozzo spumeggiante; un arcobaleno scintillava sulle acque vaporizzate. Vide anche Ethir Anduin, l'imponente delta del Grande Fiume, e miriadi di gabbiani volteggiare al sole come candidi granelli di polvere, e sotto di essi un mare verde e argento, increspato all'infinito. [...] Il suo sguardo si rivolse di nuovo a sud, ed egli contemplò Minas Tirith. Pareva molto remota, e splendida; con le bianche mura, le innumerevoli torri, troneggiava in cima alla montagna, bella e superba; le cinte scintillavano d'acciaio, sui torrioni splendevano mille bandiere. »
(SdA, libro II, cap. X)

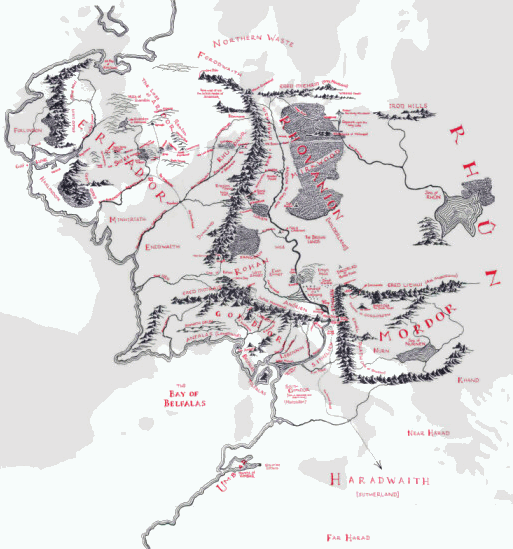
Quella che abbiamo letto è una vera e propria... carta geografica della Terra di Mezzo. Descritta a parole anziché riportata in una griglia di meridiani e paralleli, ma pur sempre una carta geografica. Una carta geografica riportante una serie di luoghi che sul nostro mondo non sono mai esistiti, naturalmente, tant'è vero che qualcuno ha parlato, a partire da Tolkien, di... "cartografia della fantasia". Lo dimostra il fiorire di atlanti, carte geografiche e mappe di ogni genere, che riproducono nei minimi dettagli l'universo creato dalla fervida fantasia di J.R.R. Tolkien, a partire da quelle disegnate dallo stesso professore a corredo delle prime edizioni dei suoi romanzi. Una delle più famose è quella che vedete qui sotto, riportata in appendice al SdA, che rappresenta non l'intera Terra di Mezzo (come a volte si ritiene), ma solo una porzione ristretta di essa, teatro delle gesta de "Lo Hobbit" e del SdA, poiché il resto è disabitato o sconosciuto (lo stesso Frodo sull'Amon Hen ha veduto « pianure senza nome e foreste inesplorate »). Per vederne una versione più ampia, cliccate su di essa:

Ecco un'altra celebre mappa tolkieniana, che si riferisce alla Prima e alla Seconda Era, e ha la caratteristica di essere "anacronistica"; in altre parole, mostra su di essa realtà che non potevano coesistere nello stesso periodo (anche in questo caso, cliccare su di essa per vederne una versione più ampia). Sulla destra infatti vediamo rappresentata la Terra di Mezzo illuminata dalle Lampade dei Valar, ma sulla sinistra osserviamo anche i due Alberi Sacri che illuminavano Aman; eppure, quando Laurelin e Telperion furono generati dal canto di Yavanna, nella notte dei tempi, le due Lampade di Illuin a nord e Ormal a sud erano già state distrutte da Melkor. Inoltre nel nord della Terra di Mezzo sono visibili sia il Beleriand che la fortezza di Angband, ma entrambi erano già spariti dalla faccia di Arda in seguito alla Guerra d'Ira, quando Númenor venne concessa agli Edain; eppure tale isola è visibile in mezzo al Belegaer, anche se senza la tradizionale forma a cinque punte come si è ormai cristallizzata nell'iconografia tolkieniana. L'Ekkaia inoltre qui appare come un mare fatto di comuni acque non dissimili dal Belegaer, anche se nessun vascello degli Uomini poteva attraversarlo, come diremo meglio in un'altra lezione. La mappa è comunque così suggestiva che meritava di comparire in questa rassegna.

Apparentemente "cartografia" e "fantasia" sembrano termini in netto contrasto fra di loro, perchè la cartografia è da sempre intesa come una scienza esatta, basata su precise misure di distanze, latitudini e longitudini, almeno fin dalla riscoperta in Europa della "Geografia" di Claudio Tolomeo, astronomo di corte dell'imperatore romano Antonino Pio (138-161), a noi già ben noto perchè lo abbiamo incontrato come autore del modello geocentrico. Al contrario la fantasia sembra avere briglia sciolta in un mondo nel quale non esistono confini o coordinate misurabili in base a principi scientifici, nel quale anzi montagne alte il doppio dell'Everest o deserti vasti come continenti possono apparire dal nulla davanti agli occhi dei lettori, se risultano necessari per l'economia del romanzo o del poema. La mente corre a questo proposito a Fantasia, l'immaginario mondo forgiato dalla penna dello scrittore tedesco Michael Ende (1929-1995): tale fantasmagorico regno, chiamato Phantásien nell'edizione originale tedesca, per ammissione dei Giganti del Cielo (i quattro venti dei Punti Cardinali) è affatto privo di confini in ogni direzione: una caratteristica che mal si concilia con i paesi della Terra, essendo limitata la superficie del nostro Pianeta. Per di più, secondo Ende a Fantàsia i concetti di "vicino" e "lontano" sono categorie sfuggenti e non quantificabili, le distanze sono concetti relativi che cambiano a seconda di chi sta viaggiando e di dove vuole andare, come è evidente nell'episodio del Tempio delle Mille Porte. Non è solo una "cartografia della mente", per usare un termine caro all'epistemologo Gaston Bachelard (1884-1962), ma addirittura una "cartografia dei desideri". Un luogo non occupa la stessa posizione per ciascuno dei suoi abitanti, ma confina contemporaneamente con tutti i luoghi in cui si trovano i viaggiatori che intendono arrivarvi. Pertanto la geografia di Fantàsia viola una delle leggi fondamentali della fisica classica, comportandosi piuttosto secondo i canoni della Relatività di Einstein, in cui ogni grandezza ha un valore che dipende sia dall'osservatore che dall'ambiente circostante! Da tutto ciò si inferisce che disegnare una carta geografica di Fantàsia è certamente impossibile, così come non è possibile disegnare una mappa del mondo di "Labyrinth - Dove tutto è possibile", film del 1986 diretto da Jim Henson (il creatore dei Muppets), dove il labirinto muta aspetto in modo imprevedibile. E allora, come mettere assieme una "cartografia della fantasia"?

In realtà, queste due parole non sono così antitetiche come potrebbe apparire a prima vista. Per comprendere il significato di tale affermazione, addentriamoci nella scienza chiamata appunto cartografia, cioè l'arte di riprodurre porzioni di superficie terrestre su di una superficie piatta. La forma della terra è molto vicina a quella di una sfera, schiacciata leggermente ai poli per via del moto diurno di rotazione; le irregolarità delle montagne e delle fosse oceaniche sono trascurabili, poiché il raggio equatoriale misura 6.378 km e il raggio polare 6.356 km, mentre la massima depressione della crosta terrestre, l'Abisso Vitjaz nella Fossa delle Marianne, sfiora gli 11 km, cioè l'1,7 per mille del raggio terrestre. Non sarà perciò troppo impreciso approssimare la Terra con una sfera la cui superficie corrisponde al livello dei mari; essa ha un raggio medio di circa 6.370 km e una superficie di 510.100.934 km². Diremo carta geografica una rappresentazione simbolica, approssimata e ridotta della superficie terrestre o di una sua parte. Si chiama scala il rapporto fra le distanze misurate sulla carta e quelle misurate sulla superficie terrestre, rapporto espresso sotto forma di frazione. Ad esempio, "scala 1 : 100.000" significa che 1 cm sulla carta equivale a 100.000 cm, cioè a 1 km, sulla superficie terrestre. A seconda della scala, le carte geografiche si distinguono in:

Il problema è quello di determinare la posizione assoluta di un punto della superficie terrestre. Per questo è stato ideato il cosiddetto reticolato geografico, un insieme di linee immaginarie perpendicolari tra loro, che avvolgono la Terra in una sorta di rete. I piani passanti per l'asse terrestre disegnano circonferenze immaginarie tutte uguali, passanti per i poli; le metà di queste circonferenze sono chiamate meridiani. Tale nome deriva dal latino meridies, "mezzogiorno", perchè in tutte le località situate sullo stesso meridiano, il mezzogiorno cade nello stesso momento. I meridiani naturalmente sono infiniti, ma per convenzione il loro numero è fissato in 360. Uno di essi è assunto come meridiano fondamentale o meridiano zero; di conseguenza vi sono 180 meridiani ad est e 180 ad ovest del meridiano zero. Poiché il reticolato geografico fu fissato quando i mari erano dominati dai vascelli dell'Impero Britannico, per convenzione il meridiano fondamentale è quello passante per Greenwich, un sobborgo di Londra; in Italia, le carte topografiche dell'Istituto Geografico Militare considerano come meridiano fondamentale quello passante per Monte Mario (Roma). I meridiani servono per la determinazione della longitudine, che altro non è se non la distanza angolare di un meridiano qualunque da quello di Greenwich, misurata in gradi, primi e secondi sull'arco di parallelo che passa per quel punto. Si parlerà di longitudine Est se il punto considerato è ad oriente del meridiano di Greenwich, di longitudine Ovest in caso contrario. I paralleli invece sono 180 circonferenze immaginarie, parallele alla linea dell'equatore; quest'ultimo è determinato sulla superficie terrestre da un piano perpendicolare all'asse della terra e passante per il centro della terra stessa, è la circonferenza massima del pianeta Terra e tutti i suoi punti sono equidistanti dai poli. Il meridiano è lungo 39.921 km, mentre l'equatore misura 40.075 km. L'equatore divide la terra in due emisferi: quello che contiene il polo nord si dice settentrionale o boreale, quello contenente il polo sud si dice meridionale o australe. Nell'emisfero boreale il Tropico del Cancro è il parallelo che congiunge tutti i punti nei quali i raggi solari sono perpendicolari al terreno nel solstizio d'estate (21 giugno), mentre il Circolo Polare Artico è quello nei cui punti i raggi solari sono paralleli al suolo nel solstizio d'inverno (21 dicembre); al contrario, nell'emisfero australe il Tropico del Capricorno è il parallelo che congiunge tutti i punti nei quali i raggi solari sono perpendicolari al terreno nel solstizio d'inverno, mentre il Circolo Polare Antartico è quello nei cui punti i raggi solari sono paralleli al suolo nel solstizio d'estate. Il nome "artico" deriva dal greco "arktos", cioè "orsa", perchè il polo nord celeste è indicato da una stella della costellazione dell'Orsa Minore. La lunghezza dei paralleli naturalmente diminuisce man mano che ci si avvicina ai poli. La latitudine di un punto è la distanza angolare di quel punto dall'equatore, misurata in gradi sull'arco di meridiano passante per quel punto. Parleremo di latitudine Nord se il punto suddetto è a nord dell'equatore, di latitudine Sud in caso contrario. La posizione di un punto sulla superficie terrestre è identificata in modo univoco da una coppia di angoli, corrispondenti a latitudine e longitudine, che vengono chiamate anche coordinate sferiche. Ad esempio la città di Washington, capitale degli Stati Uniti d'America, ha coordinate 38° 53′ 42" Nord e 77° 02′ 12" Ovest.

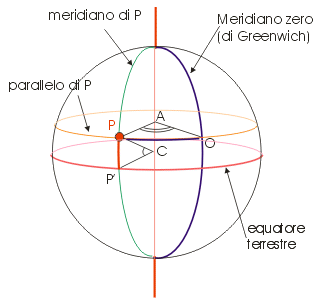
Il primo geografo che elencò una serie di località poste alla stessa latitudine, usando per la prima volta il concetto di parallelo, fu un certo Dicearco, allievo di Aristotele. L'uso di una griglia di paralleli e meridiani fu introdotto nel III secolo a.C. dall'astronomo greco Eratostene di Cirene (275-195 a.C.), anch'egli una nostra vecchia conoscenza, e si diffuse in occidente in seguito alla pubblicazione della "Geografia" di Claudio Tolomeo, opera nella quale di tutte le località sono date le coordinate sferiche. L'edizione della "Geografia" stampata a Bologna nel 1477 fu la prima nella quale compaiono carte geografiche sulle quali è disegnata una griglia di meridiani e paralleli. Ma meridiani e paralleli da soli non bastano per realizzare una carta geografica nel senso autentico della parola. Infatti il nostro pianeta è di forma sferica, dunque l'unico modo per ottenere una rappresentazione fedele del mondo è quello di costruire un mappamondo, cioè una rappresentazione anch'essa a forma di globo. Tuttavia, per distinguere i particolari del territorio occorrerebbero dei mappamondi di dimensioni notevoli, ingombranti oltre che difficili da maneggiare. E così, si ricorre alla rappresentazione del mondo o di una parte di esso su di una superficie piana, rappresentazione che dovrà per forza di cose essere approssimata, come si diceva all'inizio; l'approssimazione (cioè lo scostamento dalla realtà) è tanto maggiore quanto più vasta è la superficie da riprodurre. Per ridurre quanto più è possibile le deformazioni, si ricorre alle cosiddette proiezioni geografiche, con le quali le caratteristiche di una superficie sferica sono "proiettate" su di un piano. Le proiezioni sono di tre tipi fondamentali:

1) proiezione stereografica o di Wulff. Si chiama così in onore del mineralogo russo Yuri Viktorovich Wulff (1863-1925). Consiste nel proiettare i punti sulla superficie di una sfera da un punto P della sfera stessa su di un piano tangente alla sfera nel suo punto Q, antipodo di P. Le circonferenze ottenute intersecando la sfera con piani paralleli a quello tangente in Q vengono rappresentate sotto forma di circonferenze del piano aventi centro in Q. Unico punto fisso della proiezione è S, punto limite delle circonferenze precedenti. La proiezione stereografica è detta polare, equatoriale o obliqua a seconda che il punto P di proiezione sia un polo, un punto sull'equatore o un punto generico. Si tratta di una proiezione conforme, tuttora molto usata in cartografia.

2) proiezione cilindrica o di Mercatore. Prende il nome dal cartografo olandese Gerhard Kremer (1512-1594), che latinizzò il suo nome in Gerardus Mercator. Essa consiste nel considerare una superficie cilindrica indefinita tangente alla Terra lungo l'equatore, e proiettare i punti della superficie terrestre dal centro della Terra sulla superficie cilindrica. Tale proiezione è conforme ed è la più usata per le mappe nautiche per la sua proprietà di rappresentare le linee lossodromiche, cioè le linee che uniscono due punti qualsiasi sulla superficie terrestre tagliando tutti i meridiani con lo stesso angolo, mediante segmenti rettilinei. I meridiani inoltre sono rappresentate come rette verticali perpendicolari ai paralleli. Il suo svantaggio principale consiste nel fatto che distorce notevolmente le aree lontane dall'equatore, dilatando in maniera esagerata le distanze misurate lungo i meridiani. Ad esempio, in un planisfero di Mercatore la Groenlandia appare più vasta dell'Africa, mentre in realtà il continente africano è 14 volte più vasto della Groenlandia. La proiezione di Mercatore è tuttora quella utilizzata da Google Maps.

3) proiezione conica o di Lambert, ideata dallo svizzero Johann Heinrich Lambert (1728-1777). Essa è conforme e consiste nel sovrapporre alla superficie terrestre una superficie conica con due paralleli di riferimento che la intersecano, per poi proiettare su di essa dal centro della Terra i punti della superficie terrestre. In tal modo non c'è distorsione lungo i paralleli di riferimento, mentre essa aumenta man mano che ci si allontana da essi. I paralleli si trasformano in archi di circonferenze concentriche, mentre i meridiani si trasformano in semirette radiali a distanza costante. La proiezione di Lambert viene spesso utilizzata nelle carte aeronautiche, perché una linea retta disegnata su di essa è una buona approssimazione della rotta relativa al cerchio massimo tra i due punti di partenza e di arrivo.

4) proiezione sinusoidale o di Sanson–Flamsteed. La dobbiamo al francese Nicolas Sanson (1600-1667) e all'inglese John Flamsteed (1646-1719). È una proiezione equivalente che rappresenta i paralleli come delle rette e i meridiani come delle curve; la scala nord-sud è la stessa in ogni luogo rispetto al meridiano centrale, e quella est-ovest è la stessa in tutta la mappa; di conseguenza sulla mappa, come sulla superficie terrestre, la lunghezza di ogni parallelo è proporzionale al coseno della latitudine, e non si hanno distorsioni sul meridiano centrale né sull'equatore; le distorsioni cominciano a farsi sentire vicino ai meridiani esterni alle alte latitudini. Questa proiezione spesso è usata per la rappresentazione di stati con grande sviluppo verticale anziché orizzontale, come il Cile.

5) Proiezione di Peters. Proposta nel 1973 dallo storico tedesco Arno Peters (1916-2002), si presenta come una correzione della proiezione di Mercatore, che come abbiamo visto distorce in maniera drastica le proporzioni tra le superfici. La proiezione di Peters è concepita per mantenere tali proporzioni, attraverso una scomposizione del mondo in 100 parti orizzontali e 100 verticali; la superficie di ognuno di questi elementi è direttamente proporzionale alla reale estensione nello spazio, e i paralleli si vanno avvicinando fra di loro, anziché allontanarsi, man mano che ci si muove dall'equatore verso i poli. Con la sua carta, Peters intendeva sanare quello che secondo lui era un pregiudizio eurocentrico alla base della proiezione mercatoriana: il suo grande successo non sarebbe stato dovuto alla comodità del calcolo lossodromico, che interessa solo una parte minuscola dell'umanità, ma solo alla notevole dilatazione in essa delle regioni dell'emisfero boreale in cui erano localizzate tutte le grandi potenze coloniali: Spagna, Regno Unito, Francia, Germania, Russia e Stati Uniti d'America. In confronto ad esse, le regioni equatoriali, colonizzate dai suddetti paesi imperialisti, appaiono molto più piccole. La carta di Peters, pur deformando anch'essa i contorni dei continenti, mantiene le proporzioni tra le aree: tutti i paesi nel suo planisfero sono rappresentati in maniera equivalente, e ciò farebbe cadere la distorsione eurocentrica di Mercatore, sottolineando anzi le regioni tropicali del Terzo e Quarto Mondo, che risultano fortemente esaltate, come si vede qui sotto. Queste considerazioni spiegano il successo della carta di Peters presso organizzazioni internazionali di grande importanza come l'ONU, l'UNICEF e la Caritas, ma molti la criticano perchè la rappresentazione del nostro pianeta dovrebbe dipendere solo da considerazioni geometriche, e non politiche o geostrategiche.

Spiegata in questo modo, la questione delle coordinate sferiche e delle proiezioni cartografiche sembra piuttosto semplice. In realtà, già gli antichi Greci erano ben consci delle difficoltà legate alla determinazione della posizione di un punto sulla superficie della Terra. Determinare la latitudine non è difficile, coincidendo con la determinazione della posizione apparente del Sole a mezzogiorno, quando l'astro si trova nella sua posizione più elevata. Non è invece altrettanto semplice calcolare la longitudine, cioè la posizione a ovest o a est di un determinato punto fisso sull'equatore. Già gli antichi sapevano che, se fosse possibile stabilire il tempo locale contemporaneamente in due punti diversi, allora si sarebbe potuto determinare anche la loro distanza longitudinale. Se in un punto della Terra il sole è al meridiano, cioè l'orologio locale segna il mezzogiorno, in un punto situato 15° più ad Est il sole è passato al meridiano un'ora prima, e quindi sono le ore 13; in un punto situato a 15° ad Ovest il sole passerà al meridiano dopo un'ora, e dunque sono le 11. In un punto che dista 30° Ovest da quello scelto saranno le 10, perchè il sole passerà al meridiano dopo due ore, e così via. La Terra risulta così divisa in 24 spicchi ampi 15° di longitudine ciascuno, detti fusi orari; in realtà essi seguono non i meridiani i confini politici degli stati; ad esempio, pur estendendosi per ben 62° di longitudine (fra 73° e 135° longitudine Est), corrispondenti a quasi 5300 km, la Repubblica Popolare Cinese si trova compresa interamente dentro un unico fuso orario, quello che si trova 8 ore in anticipo rispetto a Greenwich. In un punto che dista 180° il sole passerà al meridiano dopo 12 ore (180° diviso 15° per ora significa 12 ore), e perciò sarà mezzanotte. Se proseguissimo nello stesso verso per altri 15° di longitudine, ci troveremmo in un punto della Terra in cui l'orologio segnerà le 23 del giorno prima. Esiste dunque un meridiano, opposto al meridiano zero, attraversando il quale si passa al giorno precedente se si procede verso Ovest, o al giorno successivo se si procede verso Est, rispetto al giorno di Greenwich. Questo meridiano viene detto "linea del cambiamento di data"; oggigiorno essa non segue esattamente il meridiano a 180° da Greenwich, ma ha un percorso più tortuoso, in modo da non attraversare il territorio di alcuno stato, spezzandolo in due giorni diversi.

Se ne conclude che, per la determinazione della longitudine di una località, è sufficiente conoscere l'ora di Greenwich, e quindi avere con sé un orologio sincronizzato con Greenwich, quando nella località suddetta è mezzogiorno. Se, ad esempio, l'orologio di Greenwich segna le 15, vuol dire che il luogo si trova ad Ovest di Greenwich di 3 ore (infatti a Greenwich l'orologio ha segnato mezzogiorno 3 ore prima), e che quindi la sua longitudine è 45° Ovest, poiché 15° all'ora per 3 ore ci dà 45°. Purtroppo, però, per determinare la longitudine in modo accurato bisogna avere a disposizione orologi molto precisi e stabili nel tempo; cosa più facile a dirsi che a farsi a bordo di una nave, con problemi di umidità, salsedine, scossoni dovuti alle onde... Per questo motivo la storia della determinazione della longitudine in gran parte coincide con la storia della costruzione di un orologio adatto allo scopo. Il navigatore fiorentino Amerigo Vespucci (1454-1512), nell'epoca delle grandi esplorazioni geografiche, propose per primo un metodo per il calcolo della longitudine, basato sulla congiunzione della Luna con altri pianeti, in particolare quella con Marte avvenuta il 23 agosto 1499, prevista dalle tavole planetarie in suo possesso. Galileo Galilei (1564–1642) nel 1612 suggerì invece di utilizzare la sua più importante scoperta astronomica, le lune di Giove, eclissate dal pianeta a intervalli molto regolari: delle tavole molto accurate delle eclissi delle lune di Giove per una data località poteva funzionare come un orologio del tempo locale per quella località, e permettere di calcolare la differenza di tempo e di longitudine. Osservare con grande precisione le eclissi dei satelliti medicei di Giove con un telescopio rudimentale su di una nave in movimento si rivelò però complicatissimo; si preferì perciò puntare su cronometri di precisione. I primi orologi meccanici comparvero in Europa durante la prima metà del Trecento, ma erano ingombranti e pesantissimi, non potevano essere trasportati sulle navi, ed erano assai imprecisi. Con il tempo tuttavia l'arte di costruire orologi si perfezionò, ed essi divennero più piccoli e precisi. All'inizio del Cinquecento comparvero i primi orologi da tasca, e alla metà del XVI secolo fu proposto di utilizzarli per determinare la longitudine, stabilendo il tempo locale del suo punto di partenza e quello della sua posizione corrente; eseguendo la differenza tra i due tempi si sarebbe stabilita la differenza di longitudine. Il problema consisteva nel costruirne in grado di affrontare vibrazioni, sbalzi di temperatura, mareggiate, e che nonostante questo continuasse a segnare l'ora esatta. Il problema che bisognava affrontare per determinare con esattezza la longitudine non era più matematico, ma tecnologico. Il Parlamento britannico nel 1714 arrivò a mettere in palio un premio di 20.000 sterline per chi fosse stato in grado di costruire un orologio che permettesse il calcolo accurato della longitudine: un problema centrale per una potenza marittima quale il Regno Unito stava diventando. Nel 1731 il matematico John Hadley (1682-1744) inventò il sestante, decisivo per l'esatta determinazione della longitudine, e tra il 1730 e il 1761 John Harrison (1693-1776) mise a punto dei cronometri precisissimi, i quali permisero di costruire finalmente delle carte nautiche realistiche, e contribuirono in maniera decisiva ad assicurare ad Albione un secolare predominio sui mari. Oggi, con il moderno GPS ("Global Positioning System", cioè "Sistema di Posizionamento Globale"), è possibile conoscere con grande facilità la latitudine e la longitudine di un punto qualunque della Terra: ideato nel 1973 e divenuto pienamente operativo nel 1995, originariamente consisteva in una costellazione di 24 satelliti artificiali, oggi ne comprende 31 del tipo NAVSTAR (NAVigation Satellite Timing and Ranging), disposti su sei piani orbitali con un'inclinazione di 55° sul piano equatoriale. Il principio di funzionamento si basa sulla misura del tempo impiegato da un segnale radio a percorrere la distanza tra il satellite e il ricevitore GPS, grazie all'orologio atomico presente sul satellite: il ricevitore calcola l'esatta distanza di propagazione dal satellite a partire dalla differenza (dell'ordine dei microsecondi) tra l'orario pervenuto e quello del proprio orologio sincronizzato con quello a bordo del satellite artificiale, tenendo conto della velocità di propagazione del segnale. Ciascun satellite emette segnali su due canali, allo scopo di eliminare l'errore dovuto alla rifrazione atmosferica; sono necessarie inoltre altre correzioni per via della Teoria della Relatività Generale di Albert Einstein. Anche l'Unione Europea ha in progetto la realizzazione di una propria rete di satelliti, il Sistema di Posizionamento Galileo, per scopi sia civili che militari.

A questo punto, non possiamo fare a meno di porci una domanda: è possibile sovrapporre una griglia di coordinate sferiche anche alle dettagliate mappe dell'universo di Tolkien, e in particolare alla mappa della Terra di Mezzo nordoccidentale che correda il SdA? Sfortunatamente non è così semplice come potrebbe apparire, e non solo perchè, come si può immaginare, nella Terza Era del Mondo non era ancora stato messo a punto il sistema GPS. Il fatto è che non sappiamo come sia disposta la griglia di meridiani e paralleli sulla suddetta carta, e neanche qual è la proiezione cartografica utilizzata. Come se non bastasse, vi sono discordanze tra le scale di riduzione indicate in quella del SdA e in quella dei Racconti Incompiuti, come ben esemplificato a questo link.

Nonostante queste difficoltà, il nostro amico Edoardo "Almavarno" Secco ha fatto un tentativo di sovrapporre una griglia di coordinate sferiche alla famosa mappa della Terra di Mezzo, dopo aver opportunamente "raddrizzato" la rosa dei venti in essa disegnata; il risultato lo vedete qui sotto (cliccate per ingrandire la mappa):

L'amico Almavarno ha disegnato i paralleli come un fascio di rette orizzontali, facendo riferimento a questo passo della lettera 294 scritta dal nostro Professore, da noi già letto nella lezione precedente:

« Se Hobbiville e Gran Burrone si trovano circa alla latitudine di Oxford, Minas Tirith, 600 miglia più a sud, si trova circa alla latitudine di Firenze. Le Bocche dell'Anduin e l'antica città di Pelargir allora si trovano circa alla latitudine dell'antica Troia. »
(Lettera 294 a Charlotte e Denis Plimmer)

Come abbiamo già fatto notare nella lezione precedente, J.R.R. Tolkien scrisse in più occasioni che la Terra di Mezzo si trova, o meglio si trovava, sul nostro pianeta, e che la Contea si trovava in quella che oggi è l'Europa nordoccidentale. In questo brano ad Hobbiville e Gran Burrone è attribuita più o meno la stessa latitudine; ed infatti, nella mappa di Almavarno una retta orizzontale passa per entrambe le località, confermano che si trovano praticamente sullo stesso parallelo (come Milano e Montreal nel nostro mondo!), e ciò autorizza a tracciare i paralleli come delle rette orizzontali. In particolare il nostro amico ha indicato, come equidistanti tra loro, i paralleli compresi tra 44° e 55° di latitudine Nord. Se invece la carta fosse stata realizzata con una proiezione conica, i paralleli sarebbero stati rappresentati da archi di circonferenza, la rosa dei venti avrebbe indicato il nord in un'altra direzione, e le due località di Hobbiville e Gran Burrone non si sarebbero trovate allineate lungo la direzione Est-Ovest, a meno di un'improbabile coincidenza cartografica. Nella mappa è evidenziato anche il meridiano passante per Hobbiville, in direzione perpendicolare ai paralleli, come indicato dalla rosa dei venti; il perchè è stato scelto proprio questo meridiano vi sarà chiaro tra poco.

Sulla mappa sono stati evidenziati in grassetto due particolari paralleli, quello suddetto comune al capoluogo della Contea e alla residenza di Elrond il Mezzelfo, e quello di Minas Tirith. La latitudine di Oxford corrisponde esattamente a 51° 45′ 7″ Nord, quella di Firenze a 43°46′ 17″ Nord, mentre la collina di Hissarlik (oggi in Turchia) presso i Dardanelli sulla quale sorgeva Troia si trova a 39° 57′ 27″ Nord. È possibile confrontare una carta del Mondo Secondario con una del nostro mondo, per trovare corrispondenze tra alcune famose località dell'uno e dell'altro? Eccone alcune, da Nord verso Sud:

1) a 55° Nord nel nostro universo vi sono la città di Glashow in Scozia, l'isola danese di Bornholm, Vilnius in Lituania, Mosca e Novosibirsk in Russia. Nella Terra di Mezzo vi sono il Monte Gundabad, Ered Mithrin, e nella Prima Era il Lago Mithrim, Barad Eithel, Haudh-en-Ndengin nel Beleriand (anche se nella Prima Era Arda era ancora piatta e quindi dovrebbe essere applicato un diverso sistema di coordinate sferiche).

2) a 50° Nord sulla nostra Terra vi sono la Cornovaglia, Lilla in Francia, Maastricht in Olanda, Francoforte in Germania, Praga nella Repubblica Ceca, Cracovia in Polonia, Kiev in Ucraina; nel Mondo Secondario Eregion, il corso inferiore del fiume Carnen, e nel Beleriand il banco di sabbia nella Baia di Balar, con la stessa riserva sopra ricordata.

3) a 45° Nord troviamo Milano in Italia, Lione in Francia, Zagabria in Croazia, Harbin in Cina, Hokkaido in Giappone, Portland nell'Oregon, Ottawa in Canada; nell'universo tolkieniano abbiamo invece Tol Brandir, le Paludi Morte, i Cancelli del Morannon.

4) a 40° Nord dalle nostre parti abbiamo Napoli in Italia, Madrid in Spagna, Istanbul in Turchia, Pechino in Cina, New York negli Stati Uniti d'America; nella Terra di Mezzo vi sono invece il Tolfalas meridionale e la catena degli Ephel Duath.

5) a 35° Nord ecco Malta e Creta in Europa, Teheran in Iran, Tokyo in Giappone, Santa Fe negli USA; nel Mondo Secondario troviamo invece i Porti di Umbar e la Città dei Corsari; abbiamo così percorso tutto il mondo del "Signore degli Anelli" da un'estremità all'altra.

A questo punto però ci scontriamo con una grave difficoltà. Infatti la distanza Nord-Sud tra le latitudini di Firenze e Troia è due volte maggiore di quella tra Minas Tirith e Pelargir secondo la scala della grande mappa pieghevole allegata al SdA, scala che il nostro amico ha riportato sulla sua cartina in leghe, miglia e chilometri (un miglio terrestre equivale a 1,609 km e una lega a 4,828 km). Sulla carta originale, 100 miglia sono rappresentate esattamente da 2 centimetri. E allora? Abbiamo riscontrato una contraddizione tra due scritti diversi di Tolkien?

Non necessariamente, secondo Lalaith, studiosa del Mondo Secondario creato dal nostro Autore (si veda questo link). Supponiamo difatti che la latitudine di Hobbiville sia accettata come corretta; potrebbe essere possibile che la distorsione testé segnalata sia l'effetto di una proiezione cartografica, visto che, come abbiamo visto sopra, ogni carta geografica piana finisce per essere distorta rispetto alla Terra sferica. Ma su quale tipo di proiezione potrebbe basarsi la mappa del SdA? Proviamo ad avanzare alcune ipotesi. Tanto per cominciare, il meridiano passante per Gran Burrone taglia praticamente la mappa di Almavarno in due parti uguali, il che autorizza a considerarlo il "meridiano centrale" o "meridiano zero" di questo sistema di coordinate sferiche. La cosa non appare strana, visto che Imladris (il nome Sindarin della rocca di Elrond il Mezzelfo) era un piccolo pezzo della Terra Beata di Aman trapiantato nella Terra di Mezzo, grazie al potere dell'anello elfico Vilya che Gil-galad aveva donato a Elrond, ed era il ricettacolo di tutta la sapienza degli Elfi. Il giusto equivalente di Greenwich, insomma. Così infatti si esprime Tolkien circa il reame di Elrond:

« La sua casa era perfetta, che vi piacesse il cibo, o il sonno, o il lavoro, o i racconti, o il canto, o che preferiste soltanto star seduti a pensare, o anche se amaste una piacevole combinazione di tutte queste cose. In quella valle il male non era mai penetrato. » (Lo Hobbit, cap. III)

Supponiamo inoltre che la scala lungo le linee orizzontali della griglia di meridiani e paralleli sia costante, e uguale a quella del Meridiano di Gran Burrone. Ogni linea verticale sulle mappe casa collega i punti sui paralleli alla stessa distanza dal meridiano centrale, distanza pari a 100 miglia. Questo permette di trarre conclusioni sulla proiezione utilizzata nelle mappe tolkieniane: le latitudini corrono esattamente parallele alle linee orizzontali della griglia di Almavarno, mentre le longitudini convergono progressivamente verso il bordo superiore. Ciò significa che la mappa in esame conserva le distanze, ma non le aree e le direzioni: gli angoli vengono distorti sempre più verso gli angoli superiori sinistro e destro della mappa. Solo sul meridiano centrale la direzione Sud-Nord è proiettata verticalmente in modo realistico; in qualsiasi altro punto della mappa segue invece una traiettoria parabolica che incontra il Meridiano Zero nel Polo Nord, al di là quindi del bordo superiore della mappa. Se dunque nella mappa di Almavarno volessimo tracciare anche i meridiani oltre ai paralleli, secondo Lalaith occorrerebbe rappresentare con linee curve tutti quelli diversi dal meridiano di Gran Burrone.

Stabilito questo, se vogliamo calcolare le latitudini e longitudini, i calcoli necessari sono relativamente semplici. Come si è detto, la scala della mappa del SdA è tale che 1 cm su di essa equivale a 50 miglia, cioè a circa 80 km; si tratta dunque di una scala 1 : 8.000.000, che la fa rientrare nell'ambito delle carte geografiche (vedi sopra). Sulla superficie terrestre, due gradi di latitudine distano all'incirca 111 km l'uno dall'altro. La stessa distanza separa lungo l'equatore anche due meridiani che differiscono di due gradi di longitudine, mentre essi convergono muovendosi verso Nord (o verso Sud) e si incontrano ai poli. Indicando con λ la latitudine espressa in gradi sessagesimali, la distanza tra due meridiani separati da un grado di longitudine è data dalla formula:

Sulla mappa che stiamo esaminando, 2 centimetri equivalgono a 100 miglia, cioè a circa 160 km; a quanto corrispondono 111 km? Ce lo dice la proporzione:

In questo modo, per ogni data latitudine è possibile iniziare dal meridiano centrale e localizzare sulla mappa i suoi punti d'incrocio con qualsiasi longitudine! È così che Lalaith ha tracciato sulla carta della Terra di Mezzo una griglia di paralleli e meridiani, che mette in evidenza la proiezione cartografica immaginata da quest'ultima (da questo link):

Siamo tentati dall'idea di assegnare la longitudine di 0° al Meridiano di Gran Burrone, ma Lalaith ha avuto un'idea diversa. Infatti ne "Gli Istari", uno dei capitoli della Quarta Parte dei "Racconti Incompiuti", troviamo questo passo:

« La sua frontiera orientale era approssimativamente rappresentata dal fiume Carnen alla sua confluenza con il Celduin, e quindi di Nurnen, e di là a sud fino agli antichi confini del Gondor Meridionale. (che originariamente non escludevano Mordor ...) » (Racconti Incompiuti, Parte IV)

Il Meridiano Zero, quello che separa l'Est dall'Ovest, andrebbe dunque posizionato ai confini orientali della Terra di Mezzo, puntualmente indicati da questo passo con la solita maniacale precisione di J.R.R. Tolkien. Se è così, il meridiano di Gran Burrone corrisponde a 13° Ovest, come si nota qui sopra, mentre quello di Hobbiville a 21° 30' Ovest. Noi però utilizzeremo una terza convenzione. Siccome abbiamo fatto coincidere le latitudini della Terra di Mezzo con quelle della nostra cara, vecchia Terra, perchè non fare la stessa cosa con le longitudini? Oxford dalle nostre parti si trova alla longitudine di 1° 15′ 28″ Ovest, per cui assegniamo lo stesso valore anche alla longitudine della Contea. Ne consegue che il Meridiano Zero Corre all'incirca per il Ponte sul Brandivino, e la Contea si trova ad essere praticamente il punto di partenza del computo delle longitudini! Qualcosa di molto simile a quanto avvenuto durante la Guerra dell'Anello, quando la Contea si trovò praticamente al centro delle vicende della Terra di Mezzo!

Tutte le longitudini computate con questa convenzione vanno dunque spostate di circa 20° verso ovest rispetto alla carta di Lalaith qui sopra riportata. Possiamo allora confrontare le longitudini del nostro mondo e quelle del Mondo Secondario, come abbiamo fatto prima con le latitudini? Proviamoci:

1) a 15° Ovest nel nostro universo vi sono le Canarie e Nouakchott in Mauritania. Nella Terra di Mezzo troviamo invece l'isola di Himling.

2) a 10° Ovest sulla nostra Terra vi sono Lisbona in Portogallo, Cork in Irlanda e Monrovia in Liberia; nel Mondo Secondario l'Ered Luin Settentrionale ed Harlindon.

3) a 5° Ovest ecco Siviglia in Spagna, Belfast in Irlanda, Yamoussoukro in Costa d'Avorio e l'Isola di Sant'Elena dove finì i suoi giorni Napoleone; nella Terra di Mezzo troviamo Forochel, attraverso i Colli di Evendim fino alle Bocche del Brandivino.

4) a 0° dalle nostre parti abbiamo Londra in Inghilterra, Valenza in Spagna, Nantes in Francia, Accra in Ghana, Lomè nel Togo, mentre dalle parti di Tolkien vi sono la Contea (come detto), le Paludi di Midgewater, l'Enedwaith e le montagne di Andrast.

5) a 5° Est troviamo Utrecht nei Paesi Bassi, Marsiglia in Francia, Bergen in Norvegia e Benin City in Nigeria; nel Mondo Secondario incontriamo invece Gran Burrone, gli Ettenmoor occidentali, l'Eregion, Orthanc e Anfalas.

6) a 10° Est nel nostro mondo individuiamo Milano in Italia, Amburgo in Germania, Oslo in Norvegia, Tunisi, Douala in Camerun; nel Mondo di Tolkien invece il Campo di Celebrant, l'estremità del delta dell'Entwash e l'Harondor o Gondor Meridionale.

7) a 15° Est troviamo Catania in Sicilia, Graz in Austria, N'Djamena nel Ciad, le isole Svalbard nell'Artico, Kinshasa nella Repubblica Democratica del Congo; nell'universo del SdA abbiamo invece Minas Tirith, il bordo orientale del Bosco Atro, la Montagna Solitaria e il confine orientale dell'Udun.

8) a 20° Est dalle nostre parti abbiamo Belgrado in Serbia, Varsavia in Polonia, Bengasi in Libia, Bangui nella Repubblica Centrafricana; nella Terra di Mezzo vi sono invece i fiumi Carnen o Rossacque e Celduin nel Rhovanion, e il Nurn nella Terra di Mordor.

9) a 25° Est infine ecco Heraklion in Grecia, Bucarest in Romania, Vilnius in Lituania, Helsinki in Finlandia, Gaborone in Botswana, Port Elizabeth nella Repubblica Sudafricana; nel Mondo Secondario ritroviamo invece il Mare di Rhun e gli estremi confini orientali di Mordor. Anche stavolta abbiamo percorso tutto il mondo del "Signore degli Anelli" da occidente verso oriente!

Lalaith ha provato anche a proiettare la mappa della Terra di Mezzo su uno dei nostri atlanti, facendo combaciare latitudini e longitudini, e supponendo che Hobbiville si trovi nel sito della nostra Oxford. Se la nostra amica ha ragione, la Terra di Mezzo ricopre l'Europa occidentale e il Mediterraneo tra la Scozia e la Grecia: l'area si estende da 35° a 55° Nord e da 29° Ovest a 10° Est. Ecco il risultato della sovrapposizione:

A questo link si trovano varie corrispondenze tra i luoghi immaginati da Tolkien e le località della nostra Europa. La Contea coincide con l'Oxfordshire, ed allora anche la mitica Stonehenge si trova in essa! I Rifugi Oscuri sorgono da qualche parte situata all'estremità orientale del canale di Bristol. La residenza di Tom Bombadil coincide con Clacton-on-the-sea, nell'Essex, dove sono stati ritrovati reperti risalenti al Paleolitico. Gran Burrone si trova nei pressi della città tedesca di Warendorf, nella Renania Settentrionale-Vestfalia. La casa di Beorn coincide più o meno con Magdeburgo, nella Sassonia-Anhalt. Dol Guldur è nei pressi di Norimberga. Presso Hildesheim (Bassa Sassonia) troviamo il luogo in cui Bilbo, Gandalf e i Nani sono stati salvati dalle aquile dopo l'assalto da parte degli orchi. Il Cancello Occidentale di Moria si troverebbe nei pressi di Saarbrücken, nel Saarland, dove effettivamente si trovano grandi miniere di carbone! Caras Galadhon nel Lothlorien si trovava dove oggi c'è Stoccarda. Le Cascate di Rauros potrebbero trovarsi sulla sponda meridionale del lago di Garda. Sarà una coincidenza, ma Edoras, la capitale di Rohan, è molto vicino al Monte Bianco, ed anche nella mappa della Terra di Mezzo essa è appena a nord delle Montagne Bianche! Isengard è localizzata intorno a Besançon, nella Franca Contea. Il Fosso di Helm sembra stranamente coincidere con il Massiccio del Vercors, nelle Prealpi del Delfinato. Un'altra coincidenza stupefacente: Barbalbero probabilmente abitava nella Foresta Nera! Il Monte Mindollin sembra coincidere con il Monte Falterona, al confine tra la provincia di Firenze e quella di Arezzo, da cui nasce l'Arno. Le Bocche dell'Anduin poi coincidono con le Bocche di Bonifacio, tra Sardegna e Corsica. Altra coincidenza strabiliante: le Paludi Morte potrebbero trovarsi dalle parti della laguna di Venezia! La battaglia della Piana di Dagorlad può essere avvenuta nell'attuale Friuli; è da notare che da quelle parti il 6 settembre del 394 d.C. si combatté l'importante Battaglia del Fiume Frigido, nella quale l'imperatore romano Teodosio I (l'ultimo che regnò sull'impero nella sua totalità) sconfisse l'usurpatore Flavio Eugenio e il suo magister militum, il franco Arbogaste. Le coincidenze si sprecano! Quanto a Minas Tirith, essa si trova effettivamente alla stessa latitudine di Firenze, come descritto da Tolkien, ma sul fondo del Mare Adriatico, a sud della città croata di Spalato. Osgiliath si trova nei pressi di Rimini, mentre il Cancello Nero sorge dove dalle nostre parti c'è Trieste. Monte Fato sorge invece nelle Alpi Dinariche, in Croazia, e la Torre Nera si erge nei pressi di Zagabria, in Croazia (che gli amici croati non ce ne vogliano). Il Mare di Rhûn è invece da localizzarsi nell'Ucraina occidentale. E non basta: estrapolando le coordinate oltre il bordo sinistro della mappa di Tolkien, Númenor poteva benissimo sorgere in pieno oceano Atlantico, dove oggi ci sono le Azzorre, arcipelago dipendente dal Portogallo le cui isole vengono spesso citate come le ultime porzioni emerse del continente perduto! Infine, che la Terra di Aman nella Prima e Seconda Era potesse coincidere con l'America del Nord, è speculazione di alcuni appassionati, ma senza alcun riscontro negli scritti di Tolkien.

Bisogna dire che non tutti gli studiosi di Tolkien sono d'accordo con queste identificazioni. Secondo alcuni, i calcoli di Lalaith avrebbero senso solo se la rosa dei venti non si trovasse in fondo a sinistra ma in mezzo alla mappa del SdA, proprio sul meridiano di Gran Burrone; nel caso in cui la proiezione ipotizzata da Lalaith fosse corretta, la rosa dei venti dovrebbe essere a sua volta inclinata rispetto al Meridiano Zero. Le corrispondenze geografiche sopra descritte tuttavia sono così affascinanti, che è valsa la pena di riassumerle in questa lezione. E non è finita: questa è la sede giusta per provare a rispondere ad un'altra domanda. Preso atto del fatto che la forma di Arda è cambiata nel passaggio dalla Seconda alla Terza Era, dove poteva essere localizzato il Beleriand nella nostra "geografia parallela"?

La risposta più probabile è: nel Doggerland. Pochi ne sono a conoscenza ma, durante l'ultima glaciazione (iniziata circa 110.000 anni fa e terminata 12.000 anni fa) , che in Europa è chiamata di Würm, il Mare del Nord e quasi tutte le isole britanniche erano ricoperte di ghiaccio, e il livello del mare era di circa 120 metri inferiore a quello attuale. Ne consegue che molte zone oggi sommerse erano al di sopra del livello del mare, ed anzi ricche di flora e di fauna. Tra queste vi era una vasta porzione della parte meridionale del Mare del Nord, che costituiva un'ampia pianura la quale collegava tra loro Inghilterra, Germania e Danimarca. Le prime indagini archeologiche in quest'area risalgono al 1913, e furono effettuate dal paleobiologo Clement Reid (1853-1916), che studiò resti di animali e di selci lavorate di età neolitica ai margini della zona. Oggi tale area è chiamata Doggerland per via dei banchi di sabbia presenti nella zona (Dogger Bank); tale nome è stato proposto nel 1990 dalla professoressa Bryony Coles dell'Università di Exeter, che ha anche tentato di ricostruire la mappa della zona utilizzando i dati topografici ricavati con i sonar e le prospezioni effettuate dall'industria petrolchimica nel Mare del Nord. Il fiume Reno a quell'epoca era molto più lungo di oggi, e scorreva verso nord attraversando il Doggerland; si pensa che un deposito di limo del Cenozoico nell'East Anglia rappresenti proprio l'antico letto del Reno. Gran parte del Mare del Nord e del canale della Manica era una distesa di bassa tundra; la parte settentrionale del Doggerland presentava lagune, coste e spiagge, mentre la parte interna era una vasta pianura ondulata ricca di corsi d'acqua, fiumi, paludi e laghi. Doggerland era probabilmente un habitat ricco di insediamenti umani nel periodo Mesolitico (11.000-8.000 anni fa). Particolarmente importante è il ritrovamento nel Middeldiep, una regione del Mare del Nord circa 16 km al largo della costa della Zelanda, di un cranio appartenuto a un Uomo di Neanderthal, datato oltre 40.000 anni fa. L'innalzamento del livello del mare dovuto allo scioglimento dei ghiacci causò la graduale sommersione di Doggerland, che divenne un'isola nella sua zona più elevata, l'attuale secca detta Dogger Bank, mentre la Gran Bretagna si staccò dal continente intorno al 5000 a.C. L'isola era molto estesa (circa 17.000 km²), ma estremamente bassa e priva di montagne. Nel 6200 a.C. infine un'immensa massa di ghiaccio si staccò dalle coste della Norvegia, forse a causa dell'esplosione degli idrati di metano sottomarini, e provocò un catastrofico tsunami che devastò l'isola allora ancora emersa (il cosiddetto Tsunami di Storegga), con conseguenze terribili sulle popolazioni mesolitiche. L'isola venne rapidamente sommersa per il rapido aumento del livello del mare; secondo alcuni, la sommersione di Doggerland fu alla base del mito degli Ipeborei, divenuti agli occhi degli esoterici dell'età moderna il corrispondente nordico degli Atlantidi. Appare probabile che J.R.R. Tolkien abbia avuto notizie delle scoperte sul Doggerland effettuate dai paleontologi suoi contemporanei, e dunque il racconto della distruzione del Beleriand nella Guerra d'Ira, che rileggiamo qui sotto, può essere ispirato alle moderne ricostruzioni della fine del Doggerland sotto le acque dell'Atlantico:

« Così venne posto fine al potere di Angband nel Nord, e il reame malvagio fu annichilito; e dalle profonde carceri una moltitudine di schiavi che avevano perduto ogni speranza, tornò alla luce del giorno, contemplando il mondo che era mutato. Tale infatti era stata la furia dello scontro, che le regioni settentrionali dell'occidente ne vennero infrante e il mare si precipitò rombando per molte voragini, e si ebbero confusione ed enorme fragore; fiumi scomparvero o si scavarono nuovi letti, valli si sollevarono, monti vennero livellati; e il Sirion non era più. »
(QS, cap. XXIV)

Si noti che il Sirion, il grande fiume che nasceva sul lato est degli Ered Wethrin, attraversava tutto il Beleriand lasciandosi la Foresta di Brethil ad ovest e il Doriath ad est, per poi sfociare nel Belegaer (il Grande Mare) presso le Bocche del Sirion, appare modellato proprio sull'antico corso del Reno, le cui tracce possono ancora essere ritrovate sul Fondo del Mare, salvo capovolgerne il verso di scorrimento (il Reno da sud a nord, il Sirion da nord a sud). "Sirion" e "Rhein" ("Reno" in tedesco) si somigliano anche foneticamente ed etimologicamente (indoeuropeo *Reynos, dalla radice *rey-, "scorrere", da cui anche l'inglese "river"!)

Detto questo, abbiamo compreso come sia possibile effettivamente compilare interi atlanti fantastici pieni di mappe dei meravigliosi continenti creati da Tolkien e dai suoi corifei (si pensi ad esempio alle "Quattro Terre" immaginate da Terry Brooks nel "Ciclo di Shannara"), nonostante l'apparente ossimoro costituito dall'espressione "cartografia della fantasia". È ora di passare ad un nuovo argomento; in particolare, ci occuperemo di una delle mie passioni fin da quando ero ragazzo: l'astronomia. Per continuare il percorso in mia compagnia, cliccate qui e seguitemi nel nostro viaggio attraverso le opere di Tolkien.