![]()
|
L'incendio suo seguiva ogne scintilla; (Par. XXVIII, 91-93) |
Sicuramente uno dei maggiori contributi alla nostra civiltà moderna che noi dobbiamo agli Arabi è rappresentato dall'algebra; ed è bene ricordarcene, in tempi in cui l'islamofobia sembra rendere impossibile la convivenza pacifica tra religioni e civiltà, alimentata da politicanti senza scrupoli e da terroristi che nascondono dietro una religione di facciata la loro insensata sete di potere. Il padre di questa disciplina è infatti unanimemente ritenuto il matematico persiano Muhammad ibn Musa al-Kwarizmi (780-850), intitolato "Al-Kitab al-mukhtasar fi hisab al-gabr wa'l-muqabala" ("Compendio sul Calcolo per Completamento e Bilanciamento"), anche se in realtà l'algebra era già stata ideata nel II millennio a.C. da egiziani e babilonesi, e poi portata avanti dal greco Diofanto di Alessandria (III-IV secolo d.C.) e dall'indiano Brahmagupta (598–668). In ogni caso il termine "algebra" risale proprio ad al-Kwarizmi, derivando da quell'"al-gabr" nel titolo del suo trattato, che significa "il completamento" (cioè il procedimento che consiste nell'aggiungere la stessa quantità ad entrambi i membri di una equazione). Egli ebbe inoltre il merito di sistematizzare la disciplina, come fece Euclide con la geometria; e proprio nella forma che egli le aveva dato essa passò in eredità alla matematica occidentale, attraverso la traduzione che ne fece l'inglese Roberto di Chester nel 1145, sotto il titolo di "Liber algebrae et almucabala". Si noti che il termine "algebra" è giunto sino a noi, "almucabala" no (eppure l'arabo "al-muqabala" significa "il bilanciamento" e consiste nel portare le quantità dello stesso segno nello stesso membro di una equazione: un concetto ben noto all'algebra moderna).
Notevoli contributi all'algebra diedero anche l'egiziano Abu Kamil Shuja ibn Aslam (850-930); il persiano Abul Wafa Buzjani (940-998); l'iracheno Abu 'Ali al-Hasan ibn al-Hasan ibn al-Haytham (965-1038), noto in Europa come Alhazen, del quale riparleremo a proposito dell'ottica; il persiano Abu al-Rayhan Muhammad ibn Ahmad al-Biruni (973-1048); il persiano Omar al-Khayyam (1048-1131), noto anche per le sue poesie d'amore; e il persiano Sharaf al-Din al-Muzaffar al-Tusi (1135-1213), fondatore della cosiddetta geometria algebrica. Il primo grande algebrista europeo fu Leonardo Fibonacci di Pisa (1170-1240), che nel suo "Liber Abaci" fu tra i primi a far conoscere i numeri arabi in Occidente. Tra i contemporanei di Dante il fiorentino Paolo Gherardi, nel suo "Libro di ragioni" (1328), e Mastro Dardi di Pisa, nella sua "Aliabraa Argibra" (1344), fornirono le soluzioni per alcuni particolari tipi di equazioni di terzo grado. Il primo a trovare la formula risolutiva generale per tutte le equazioni di terzo grado fu il bolognese Scipione dal Ferro (1465-1526), ma non la pubblicò. Il bresciano Niccolò Fontana (1499-1577), detto Tartaglia per la sua balbuzie, ritrovò autonomamente la soluzione, ma attese a pubblicarla perchè all'epoca i matematici usavano pubblicare un'unica opera enciclopedica, contenente tutti i risultati da loro ottenuti nella loro vita, e per scriverla occorrevano anni. Il pavese Gerolamo Cardano (1501-1576) nel 1539 ottenne che Tartaglia gliela rivelasse, nascosta tra i versi di un sonetto, dietro giuramento di non pubblicarla prima di lui, ma nel 1545 egli la pubblicò per primo nella sua "Ars Magna", cosa che provocò una lunga querelle tra i due algebristi; oggi quella formula è detta di Cardano-Tartaglia. Applicando questa formula, Raffaele Bombelli (1530-1572) si trovò nella necessità di operare con le radici quadrate di numeri negativi, ed inventò i numeri immaginari e complessi. Ludovico Ferrari (1522-1565), allievo di Cardano, fu il primo a trovare una formula risolutiva generale per le equazioni di quarto grado.
Come si vede da questi brevi cenni, lo scopo dell'algebra consiste nella risoluzione di equazioni e sistemi di equazioni simboliche, cioè contenenti quantità che a priori possono avere qualunque significato numerico. Oggi queste quantità vengono indicate con lettere: ad esempio la x e la y indicano tradizionalmente due incognite. Inizialmente però il procedimento simbolico non era utilizzato, e tutto veniva espresso a parole. Ad esempio, l'equazione x2 = 2x + 8 era così scritta: « il quadrato dell'incognita è pari al doppio dell'incognita aumentato di 8 » (è facile verificare che le soluzioni questa equazione sono x1 = – 2 ed x2 = 4). Il primo ad adottare unicamente una notazione algebrica simbolica fu François Viète (1540-1603) nel suo trattato "Isagoge in artem analyticam" (1591). Nel 1799 Carl Friedrich Gauss (1777-1855), detto "il Principe dei Matematici" e ritenuto da molti il più grande matematico di ogni tempo, dimostrò il cosiddetto Teorema Fondamentale dell'Algebra: « ogni equazione algebrica di grado n ammette n soluzioni, considerando quelle reali, quelle complesse e quelle molteplici ». Infine, nel gennaio del 1831, a meno di vent'anni di età, il ragazzo prodigio Évariste Galois (1811-1832) dimostrò l'impossibilità di risolvere "per radicali" le equazioni di grado superiore al quarto. Ma torniamo ora all'epoca di Dante.
Nell'opera dantesca non si trovano diretti riferimenti alla risoluzione di equazioni, eppure non ci sarà difficile trovare persino l'algebra, nascosta « sotto 'l velame de li versi strani » (Inf. IX, 63). Quanto infatti il poeta e Beatrice giungono nel Primo Mobile (ne riparleremo più avanti), così la seconda spiega al primo:
« Non è suo moto per altro distinto,
ma li altri son mensurati da questo,
sì come diece da mezzo e da quinto » (Par. XXVII, 115-117)
Cioè: il movimento del Primo Mobile (del quale riparleremo a proposito della cosmologia dantesca) non è determinato dal movimento di qualcos'altro, ma tutti gli altri moti ricevono la loro misura da esso, e si ragguagliano ad esso così come... come esprimere la sincronizzazione del moti delle sfere celesti con quello del Primo Mobile? Il Sommo Vate non può che ricorrere ad una similitudine matematica: come il dieci è misurato dalla sua metà e dalla sua quinta parte. Misurato qui sta per "ottenuto tramite moltiplicazione". E qual è il numero che è "misurato" in tal modo dal suo mezzo e dalla sua quinta parte?
Indichiamo tale numero con x. La sua metà è x/2, la sua quinta parte è x/5, dunque se ne ricava l'equazione:
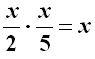
che con facili passaggi diventa:
![]()
si tratta di un'equazione di secondo grado spuria, le cui soluzioni sono x1 = 0 ed x2 = 10. La prima è ovviamente non accettabile; se ne conclude così che l'unico numero "misurato" dalla sua metà e dalla sua quinta parte è proprio il "diece". Come volevasi dimostrare!
Per chiudere questo discorso mostrando quali fecondi sviluppi ha avuto la Matematica ai nostri giorni, è utile citare questo brano tolto dal saggio « I poblemi del millennio » del matematico Keith Devlin:
« Una comune concezione errata è l'idea che la Matematica abbia prevalentemente a che fare con l'esecuzione di calcoli [...] A metà del XIX secolo, tuttavia, ebbe luogo una rivoluzione. Uno dei suoi epicentri fu la piccola città universitaria tedesca di Göttingen, dove i leader universitari erano i matematici Lejeune Dirichlet (1805-1859), Richard Dedekind (1831-1916) e Bernhard Riemann (1826-1866). Nel loro nuovo modo di concepire la Matematica, il suo interesse fondamentale non stava nell'esecuzione di un calcolo o nel trovare una soluzione, quanto piuttosto nella formulazione e nella comprensione di concetti e relazioni astratte; in altre parole, si assisteva a uno spostamento di accento dal fare al comprendere, dal risolvere un'equazione al "pensare per concetti (il "Denken in Begriffen" di Riemann). (...) L'emergere, stranamente silenzioso, della Matematica Moderna fa affiorare alla mente le parole del narratore tedesco Wilhelm Raabe (1831-1910): "Quando un fiore si apre, non fa rumore!" (...)
La definizione che meglio descrive la Matematica contemporanea è quella di "scienza dei modelli". Fra le numerose branche della Matematica odierna, le più conosciute solo la Teoria dei Numeri (lo studio dei modelli di numeri), la geometria (lo studio dei modelli delle forme), la trigonometria (che prende in considerazione la misura delle forme), l'algebra (che studia modelli di associazione di oggetti), il calcolo infinitesimale (i modelli di moto e variazione continui), la topologia (modelli di vicinanza e posizione relativa), il calcolo delle probabilità (modelli di ripetizione negli eventi casuali), la statistica (modelli di dati raccolti nel mondo reale) e la logica (modeli di ragionamento astratto). (...)
A metà ottocento, ad esempio, i matematici cominciarono a studiare le proprietà delle funzioni astratte, specificate non da una formula, ma dal loro comportamento. Questo approccio si rivelò particolarmente fecondo nello sviluppo del calcolo infinitesimale, nel quale Riemann parlò del raggiungimento di "un punto di svolta nella concezione di infinito."
»
![]()
E proprio di infinito ora vogliamo parlare. L'infinito è uno dei concetti matematici che più frequentemente ritorna nelle opere dei grandi letterati, soprattutto in epoca romantica. Basti pensare al celeberrimo "Infinito" di Giacomo Leopardi, a "Vita ed opinioni di Tristam Shandy" di Laurence Sterne o alla "Biblioteca di Babele" di Jorge Luis Borges. Trattandosi di una realtà tanto lontana dall'esperienza umana, spesso poeti e scrittori si rivolgono alla matematica per riuscire a rendere in termini più realistici il loro "naufragare" nel mare dell'infinito. E chi più di Dante, fra tutti i poeti che annovera la millenaria storia della letteratura italiana, si è trovato nella necessità di spiegare ai suoi lettori il concetto di infinito, dato che tutto, nel suo Oltremondo, sembra essere caratterizzato dal fatto di non avere fine? Non ha fine né il tormento dei dannati né la beatitudine dei salvati; non ha fine il Cielo Empireo, non ha fine la Bontà di Dio, e ovviamente sembra non avere fine neppure il numero degli Angeli.
Qui giungiamo al punto che ci interessa, perché spesso i teologi si sono interrogati sul reale numero delle creature angeliche, senza riuscire ad andare al di là di termini come "innumerevoli", "in numero sterminato", "incalcolabili", e via elencando. Era logico pensare che anche l'Alighieri avrebbe voluto dire la sua in proposito, dal momento che i canti XXVIII e XXIX del Paradiso sono interamente dedicati alla dottrina degli angeli: in essi Dante osserva le categorie angeliche che presiedono ai nove cieli del Paradiso, disposte secondo nove cerchi concentrici in perpetuo movimento: da ognuno di essi, come da un crogiuolo di ferro incandescente, un numero strabiliante di scintille si stacca dal proprio cerchio, in modo che gli angeli si distinguano uno a uno, pur continuando a seguirne il movimento. Ora, il nostro autore vuole rendere l'immagine di un numero grandissimo, tendente ad infinito, così alto che la classica numerazione romana (basata su I, V, X, L, C, D, M) è impossibilitato ad esprimerlo. Per riuscirci, evitando qualsiasi banalizzazione dell'immagine, la sua genialità artistica ha deciso di far ricorso proprio all'universo della Matematica. Ma il concetto di passaggio al limite per x tendente all'infinito non era noto a quell'epoca; e così la possente fantasia dantesca, strettamente legata al potere visivo delle parole, fa ricorso ad un episodio leggendario, legato nientemeno che alla storia degli scacchi.
 ù
ù
I cori angelici, incisione dall'edizione della Divina Commedia pubblicata da
Bernardino Benalio e Matthio da Parma, Biblioteca Nazionale di Firenze
Cosa c'entrano gli scacchi con l'infinito? Ora lo scopriremo. Com'è noto, le origini degli scacchi si perdono nella notte dei tempi e nessuno può dire con certezza dove e quando furono inventati. Al proposito esistono varie teorie, ma secondo l'ipotesi più accreditata furono inventati in Persia o in India. Antichi poemi persiani risalenti circa al VI-VII secolo d.C. descrivono, talvolta anche in dettaglio, un antico gioco da tavolo, lo Shatranj, derivato da un gioco ancor più antico e di provenienza indiana, lo Chaturanga; entrambi sembrano molto simili al moderno gioco degli scacchi. Alcuni storici ritengono che lo Chaturanga derivi a sua volta da qualche gioco cinese, ma non ci sono prove in proposito. Nel 1972 nell'Uzbekistan del Sud, presso la località di Afrasaib, furono riportati alla luce antichi pezzi dello Chaturanga, datati al 760 d.C. circa. I pezzi di Afrasaib sono finemente lavorati, quindi con grande probabilità risalgono ad un periodo storico in cui lo Chaturanga era già molto popolare. È perciò pressoché certo che le origini dello Chaturanga siano ben più antiche, forse addirittura al I o II secolo d.C.
Con il trascorrere del tempo il nome e le regole dell'originale Chaturanga cambiarono progressivamente. In ogni caso la diffusione del nuovo gioco fu assai rapida, anche grazie ai carovanieri, ansiosi di portare nelle loro patrie ogni possibile novità; fu così che gli arabi diffusero il nuovo gioco in tutti i territori da essi colonizzati. Le prime testimonianze scritte di epoca medioevale risalgono all'incirca all'anno 1000 d.C. e sono di provenienza iberica, dato che proprio lì era più frequente l'incontro tra arabi ed europei. Inizialmente gli scacchi furono avversati come usanza musulmana, e quindi (nella mentalità dell'epoca) di origine demoniaca; San Pier Damiani (1007-1072), grande riformatore e moralizzatore della Chiesa del suo tempo, li combatté nelle sue prediche, e Papa Alessandro II (1061-1073) arrivò a proibirli con un editto, considerandoli un gioco d'azzardo. Infatti in Europa era stato aggiunto agli scacchi l'uso dei dadi per determinare quale mossa si dovesse compiere, snaturando in tal modo le regole originali, basate sulla mera logica ed abilità. Negli anni successivi tuttavia la dipendenza dagli scacchi fu eliminata, le proibizioni ecclesiastiche caddero ed il gioco si diffuse fra i ceti più elevati, tanto che innumerevoli poemi cortesi citano gli scacchi nei loro versi. Furono composte intere opere ad essi dedicate, come il francese « Les échecs amoureux » ed il « Liber de moribus hominum et officiis nobilium super ludo scachorum ». Quest'ultimo fu scritto dal domenicano frate Jacopo da Cassole, morto verso il 1325, dunque contemporaneo di Dante, ed in esso gli scacchi sono usati addirittura come fonte di ammaestramenti morali. Forse la sua opera era nota all'Alighieri, che ben conosceva anche la leggenda circolante intorno all'origine del gioco. Vale la pena di raccontarla.
Si narra che lo Shah di Persia (la leggenda come al solito non specifica quale) perdette un figlio nel corso di una guerra e non riusciva a consolarsi per la sua morte. Siccome il sovrano intristiva e trascurava gli affari dell'impero, la corte chiese al matematico Sissa Nassir di inventare qualche nuovo passatempo per distrarlo e fargli così dimenticare il lutto subito. Detto, fatto: Sissa Nassir si mise all'opera ed inventò gli scacchi. Inizialmente il sovrano di Persia fu freddo, ma poi cominciò ad appassionarsi al gioco e rientrò in se stesso. Lieto perchè Sissa Nassir gli aveva fatto un così bel dono, gli disse: « Come ricompensa chiedimi ciò che vuoi, e l'avrai! » A quel punto Sissa Nassir rispose: « O Re dei Re, prendi la scacchiera che ti ho donato e poni su di essa un chicco di grano nella prima casella, due nella seconda, quattro nella terza, otto nella quarta, e via raddoppiando fino alla sessantaquattresima; metti tutto il grano in un sacco e dammelo. »
Allo Shah la richiesta apparve lì per lì esageratamente modesta, e gli propose invece di donargli una provincia del suo impero, ma Sissa Nassir fu irremovibile. Allora il Re chiamò i suoi contabili ed ordinò loro di fare il calcolo e di dare al matematico i « cento chicchi di grano » che egli aveva richiesto.
Dieci minuti dopo chiamò i contabili e chiese loro se avessero effettuato il calcolo, ma essi risposero: « Lo stiamo incominciando. » Li interpellò di nuovo dopo due ore ed essi risposero: « Abbiamo appena iniziato. » Fu a questo punto che lo Shah cominciò a sospettare che Sissa Nassir lo avesse messo letteralmente nel sacco.
Dopo due settimane di calcoli, i contabili furono ricevuti dall'imperatore, che chiese loro se avessero terminato il calcolo; essi annuirono. « Bene. Quanto grano ha chiesto Sissa Nassir? Ce n'è abbastanza nei granai reali per accontentarlo? »
A questo punto il capo dei contabili rispose: « Mio signore, per dare a Sissa Nassir tutto il grano che ha richiesto, tu dovresti spianare tutte le montagne della Terra, tagliare tutte le foreste, colmare tutti i mari, prosciugare tutti i fiumi, radere al suolo tutte le città, e coltivare a grano l'intera superficie della Terra per 1500 anni consecutivi. »
Lo Shah restò di stucco: evidentemente non aveva idea di quanto sia vertiginosa la crescita di una funzione esponenziale. Il problema posto da Sissa Nassir ai contabili reali consisteva infatti nello stabilire la somma dei primi 64 termini di una progressione geometrica di ragione 2.
![]()
Si dice progressione geometrica una successione di numeri tale che il rapporto tra un termine della successione e il precedente sia costante. Ad esempio { 3, 6, 12, 24, 48, 96, 192, 384, 768, 1536, 3072, 6144... }, perchè:
6/3 = 2
12/6 = 2
24/12 = 2
e così via. I termini successivi di una progressione si possono indicare con lettere minuscole con pedice:
{ a1 , a2 , a3 , ..., an , ... }
Il rapporto costante (nell'esempio numerico 2) tra ogni termine della successione e il precedente si chiama ragione della progressione geometrica, e si indica con q. In altre parole:
an = an–1 x q
Ne segue facilmente la formula per calcolare il termine n-esimo di una progressione geometrica conoscendo il primo termine a1 e la ragione q:
an= a1 x qn–1 (1)
Per calcolare la somma Sn dei primi n termini di una progressione geometrica bisogna ricorrere a una nota formula algebrica, che dà la scomposizione della differenza di due potenze dello stesso grado:
qn – 1 = ( q – 1 ) x ( qn–1 + qn–2 + qn–3 + ... + q3 + q2 + q + 1 ) (2)
Usiamo ora la proprietà (1):
Sn =
a1 + a2 + a3 + ... + an =
= a1 + a1 x q + a1 x q2
+ a1 x q3 + ... + a1 x qn–1 =
= a1 x ( 1 + q + q2 + q3
+ ... + qn–1 )
e quindi, dalla (2):
Sn = a1 x (qn – 1)/(q – 1) (3)

Dunque per risolvere il problema di Sissa Nassir bisogna trovare la somma dei termini di una progressione geometrica di ragione 2 il cui primo termine vale 1. Usando la formula (3) si ha:
S64= 1 x (264 – 1) / ( 2 – 1 ) = 264 – 1 = 18.446.744.073.709.551.615
Si tratta indiscutibilmente di un risultato mostruosamente grande, che nel nostro sistema di numerazione richiede 19 cifre per essere scritto! L'unico modo per esprimerlo in lingua italiana è il seguente: 18 miliardi di miliardi, 446 milioni di miliardi, 744 milioni di milioni, 73 miliardi, 709 milioni, 551 mila e 615. Dante, che conosceva bene questo aneddoto, può così affermare:
« E poi che le parole sue restaro,
non altrimenti ferro disfavilla
che bolle, come i cerchi sfavillaro.
L'incendio suo seguiva ogne scintilla;
ed eran tante, che 'l numero loro
più che 'l doppiar de li scacchi s'immilla » (Par. XXVIII, 88-93)
Il verbo "immillare" qui usato è stato coniato da Dante stesso (come « s'incinqua » di Par. IX, 40 e « s'intrea » di Par. XIII, 57), creatore di parole e non solo di versi, come si confà al padre della letteratura italiana, e vuol significare che il numero degli angeli « cresce in più migliaia » (come scriveva il Buti nel suo commento). Come si è detto nel capitolo precedente, quando Dante pensa a grandi numeri, gli viene sempre in mente la parola "mille". Probabilmente però qui egli è stato suggestionato anche da un noto passo del libro di Daniele:
« Un fiume di fuoco scendeva dinanzi a Lui, mille migliaia Lo servivano e diecimila miriadi lo assistevano » (Dan 7, 10)
e da un altro dell'Apocalisse:
« Durante la visione poi intesi voci di molti angeli intorno al trono e agli esseri viventi e ai vegliardi. Il loro numero era miriadi di miriadi e migliaia di migliaia » (Ap 5, 11)
Alcuni però ritengono che questo "immillarsi" abbia un significato matematico più preciso. Sulla scorta di un'affermazione di San Tommaso d'Aquino:
« Multitudo angelorum trascendit omnem materialem multitudinem
»
[La moltitudine degli angeli supera ogni moltitudine materiale] (Summa Theologica I, CXII, 4)
è possibile che Dante non fosse ancora soddisfatto dell'iperbolico numero rappresentato dal « doppiar de li scacchi », e così abbia pensato di sostituire alle potenze del due le potenze del mille. In altre parole, se sulla prima casella della scacchiera mettiamo un angelo, sulla seconda ne mettiamo non due ma mille, sulla terza mille per mille, cioè un milione, sulla quarta un milione per mille, cioè un miliardo, e così via fino alla sessaquattresima. In tal modo gli angeli invece che raddoppiare si "immillano"! Dunque il problema di Sissa Nassir si trasforma in quello di trovare la somma dei primi 64 termini di una progressione geometrica il cui primo termine è 1 e la ragione vale 1000. La formula (3) ci dà allora:
S64= 1 x (100064 – 1) / ( 1000 – 1 ) = ( 10192 – 1 ) / 999 = circa 1,001 x 10189
Con la notazione decimale,
questo numero andrebbe così scritto:
1.001.001.001.001.001.001.001.001.001.001.001.001.001.001.001.001.001.001.
001.001.001.001.001.001.001.001.001.001.001.001.001.001.001.001.001.001.
001.001.001.001.001.001.001.001.001.001.001.001.001.001.001.001.001.001.
001.001.001.001.001.001.001.001.001.001!
Un numero decisamente al di là di ogni possibilità di conteggio, dato che la massa in grammi dell'universo oggi conosciuto arriva « appena » fino a 1058, e il numero di protoni nell'universo conosciuto giunge « solo » a 1081! Ancora una volta, l'Alighieri ha dimostrato si saper affiancare l'abilità di maneggiare i numeri all'immancabile creatività linguistica. Davvero si può affermare che la Divina Commedia è la sintesi dell'intero scibile medioevale, non solo dal punto di vista letterario, ma anche scientifico!
Una piccola curiosità prima di proseguire. Quanto vale "millanta"? Questa antica parola toscana indica un numero indefinito e molto grande rispetto al contesto nel quale il termine è usato, spesso con intonazione scherzosa. In Dante non la si trova mai, ma è usata ad esempio dal Boccaccio: « Disse allora Calandrino: "E quante miglia ci ha?" Maso rispose: "Haccene più di millanta, che tutta notte canta." » (Decameron, Giornata VIII, novella 3) Si pensa che tale termine, oggi un po' desueto, derivi dall'unione della parola mille con il suffisso "-anta" che evoca le decine da quaranta a novanta. Peraltro il termine è all'origine del verbo "millantare", letteralmente amplificare di mille volte, che è usato per indicare l'atto di vantarsi eccessivamente, di esagerare un'affermazione fingendo che sia vera!
![]()
E non finisce qui. Leggiamo infatti l'esordio del Canto VI del Purgatorio, nel quale Dante e Virgilio devono districarsi a fatica dalla ressa delle anime dei negligenti periti di morte violenta, che si affollano intorno a loro come i postulanti che fanno cerchio intorno a chi esce vittorioso dal gioco d'azzardo, invocando da quel vivente preghiere e suffragi perché venga abbreviata la loro permanenza nell'Antipurgatorio. La similitudine è tratteggiata con grande realismo, attraverso il racconto di una scenetta di vita quotidiana, a cui il Poeta dovette certamente assistere più volte lungo le strade:
« Quando si parte il gioco de la zara,
colui che perde si riman dolente,
repetendo le volte, e tristo impara;
con l'altro se ne va tutta la gente;
qual va dinanzi, e qual di dietro il prende,
e qual dallato li si reca a mente;
el non s'arresta, e questo e quello intende;
a cui porge la man, più non fa pressa;
e così da la calca si difende.
Tal era io in quella turba spessa,
volgendo a loro, e qua e là, la faccia,
e promettendo mi sciogliea da essa. » (Purg. VI, 1-12)
In questi versi alcuni commentatori hanno voluto riconoscere un primo abbozzo, per quanto ingenuo, di calcolo delle probabilità: dall'atteggiamento del giocatore perdente che riflette sulla frequenza delle uscite di certi numeri, emerge il concetto embrionale di frequenza di un evento casuale.

L'incontro di Dante con Pia dei Tolomei nell'Antipurgatorio secondo il Dorè
Il primo ad occuparsi di una analisi matematica delle probabilità fu probabilmente Gerolamo Cardano (1501-1576), già citato sopra come algebrista, che a quanto pare fu travagliato per tutta la vita dai problemi economici, e per risolverli si dedicò ai giochi d'azzardo. Per questo nel 1526 scrisse il "Liber de ludo aleae", che però fu pubblicato solo un secolo e mezzo dopo, nel 1663. Anche quel genio di Galileo Galilei scrisse un libello "Sulla scoperta dei dadi", pubblicato postumo nel 1656. La paternità del moderno calcolo delle probabilità è però divisa equamente fra i francesi Blaise Pascal (1623-1662) e Pierre de Fermat (1601-1665). Com'è noto, gli studi di Pascal presero avvio dai problemi che gli poneva uno dei suoi amici, il Cavaliere de Méré, accanito giocatore d'azzardo, il quale passò alla storia per essersi chiesto se era più probabile ottenere almeno un 6 in 4 lanci di un dado non truccato o almeno un doppio 6 in 24 lanci. Per risolvere tale quesito ed altri simili, Pascal avviò una corrispondenza con Fermat, dalla quale in una lettera del 29 luglio 1654 scaturì il concetto di probabilità come rapporto fra il numero di casi favorevoli ad un evento e il numero totale di casi possibili.
Nel 1657 l'olandese Christiaan Huygens (1629-1695) scrisse il "Libellus de ratiociniis in ludo aleae", il primo vero trattato sul calcolo delle probabilità, mentre nel 1713 fu pubblicata postuma l'"Ars conjectandi" di Jakob Bernoulli (1654-1705), nella quale egli enunciava la cosiddetta Legge dei Grandi Numeri: all'aumentare del numero di prove, la frequenza con cui un evento si presenta tende ad avvicinarsi alla probabilità calcolata da Pascal. Successive ricerche vennero compiute da Abraham de Moivre (1667-1754) e da Pierre Simon de Laplace (1749-1827), mentre lo statistico Bruno de Finetti (1906-1985) introdusse la definizione soggettiva della probabilità, secondo cui essa è il grado di fiducia che una persona ha nel verificarsi dell'evento (qualcosa dunque che riguarda molto da vicino i moderni bookmakers). Infine il sovietico Andrei Kolmogorov (1903-1987) con il suo saggio del 1933 intitolato "Grundbegriffe der Wahrscheinlichkeitsrechnung" ("Concetti fondamentali del Calcolo delle Probabilità") fondò la moderna teoria assiomatica della probabilità, dandole un fondamento logico che superava e generalizzava le diverse definizioni pascaliana, frequentista e soggettiva.
Come si vede, al tempo di Dante un calcolo esatto delle probabilità non esisteva ancora, ma siccome il gioco d'azzardo è vecchio quanto il mondo, sicuramente esistevano già conoscenze empiriche intorno alle probabilità che si avevano di vincere giocando in un certo modo. Certamente il gioco d'azzardo più diffuso era quello dei dadi, la cui origine è sconosciuta, ma probabilmente asiatica, dato che sono già citati nei Rig-Veda, composti fra il 2000 e il 1500 a.C. I Greci giocavano con dadi di osso, ricavati dagli astragali (ossa del tarso) di capra; molti vasi greci mostrano gli eroi omerici intenti a divertirsi con questo gioco, e la tradizione ne faceva risalire l'invenzione al dio Hermes oppure all'astuto Palamede (infatti "palamaomai" vuol dire "ordire", "macchinare"), l'unico che riuscì a farla in barba al furbissimo Ulisse, smascherandolo quando si era finto pazzo per marcare visita alla Guerra di Troia, come narrava Euripide (480-406 a.C.). Palamede avrebbe ideato il gioco dei dadi durante una carestia sopravvenuta nel corso dell'assedio di Troia, per distrarre gli Achei dalla penuria di cibo. Si noti che questo, secondo Erodoto, è lo stesso motivo per cui i Lidi avrebbero inventato i dadi ed altri giochi d'azzardo:
« Sotto il regno di Atis, figlio di Mane, si era abbattuta su tutta la Lidia una terribile carestia: per un po' i Lidi avevano resistito, ma poi, visto che la carestia non aveva fine, cercarono di ingannare la fame inventando una serie di espedienti. E appunto allora sarebbero stati ideati i dadi, gli astragali, la palla e tutti gli altri tipi di gioco: un giorno lo trascorrevano interamente a giocare per non sentire il desiderio di mangiare, il successivo lasciavano perdere i divertimenti e si cibavano. » (Storie, I, 94)
Questo gioco era inoltre popolarissimo presso i Romani: quando volle dare inizio alla sua ribellione contro il Senato varcando il Rubicone, Giulio Cesare sbottò nella celebre esclamazione "Alea jacta est!" ("il dado è lanciato!"), e persino sul Golgotha la veste di Gesù Cristo fu giocata ai dadi tra i soldati romani. Così si esprime Marco Tullio Cicerone (106-43 a.C.):
« Quid est tam incertum quam talorum iactus? Tamen nemo est quin saepe iactans Venerium iaciat aliquando, non numquam etiam iterum ac tertium.
»
[Cosa vi è di più incerto del lancio dei dadi? Eppure ci sono giocatori che, a volte, ottengono una Venere, e persino due o tre volte di seguito.] (De Divinatione II, 59)
I Romani chiamavano "Venere" il lancio di quattro dadi che sortiscono facce tutte diverse tra di loro: un caso che ha solo 5 probabilità su 432 di verificarsi. Le scommesse sui dadi furono oggetto di molte leggi romane: una di esse proibiva di intentare causa da parte di una persona che permetteva il gioco d'azzardo nella sua casa, anche se era stata imbrogliata o ferita. La passione per questo gioco contagiò ovviamente il Medioevo, divenendo oggetto di severi ed insistenti (quanto inutili) divieti da parte della Chiesa e degli statuti comunali; il Re di Francia San Luigi IX (1214-1270) tentò di proibirli per ben due volte, nel 1254 e nel 1256. Ai dadi giocavano anche gli arabi, ed infatti dall'arabo "zahar", "dado", deriva verosimilmente il nome del gioco della zara, oltre al termine "azzardo".

Achille e Aiace giocano ai dadi, particolare di
un vaso greco del VI sec. a.C., Musei Vaticani
Il gioco della zara era diffusissimo nel Trecento, e si giocava gettando tre dadi e tentando di indovinare i numeri risultanti dalle loro possibili combinazioni. I numeri sotto il 7 e al di sopra del 14, erano considerati nulli. Così scriveva in proposito Francesco Buti, commentatore del XIV secolo:
« Li punti divietati sono in tre dadi esclusive da sette in giù e da quattordici in su; e però quando vegnano quelli punti, diceno li giocatori: Zara; quasi dica: Nulla, come Zero nell'abaco, e questi sono vietati, perché non hanno tre parità come ha sette e quattordici e li punti che sono in quel mezzo. »
Dalla moderna analisi del gioco si ricava che il 10 e l'11 sono i numeri che hanno probabilità maggiori di uscire, mentre il 3 e il 18 hanno quella minore. Questi ultimi due infatti si possono ottenere solo con tre uni o con tre sei. Il caso favorevole è dunque uno solo; quanti sono quelli possibili? A ciascuna delle sei facce del primo dado va associata ciascuna faccia del secondo e ciascuna faccia del terzo, per cui questi casi sono in tutto 6 x 6 x 6 = 216. Secondo la definizione classica di Pascal, la probabilità è pari ad 1/216. Il 4 ha probabilità di uscita tripla, perchè esso si può ottenere con una delle seguenti combinazioni di risultati: {1,1,2} o {1,2,1} o {2,1,1}. Sono tre, mentre i casi possibili restano 216, e quindi la probabilità di sortirlo è 3/216 = 1/72. Nel Medioevo tuttavia questi tre casi erano considerati uno solo (due dadi che danno 1 ed uno che dà 2), e quindi il punteggio 4 era considerato nullo perchè, come il tre, proveniva da una sola combinazione possibile di eventi.
Con i seguenti versi:
«
Quando si parte il gioco de la zara,
colui che perde si riman dolente,
repetendo le volte, e tristo impara;
con l'altro se ne va tutta la gente;
qual va dinanzi, e qual di dietro il prende,
e qual dallato li si reca a mente » (Purg. VI, 1-6)
Dante intende dirci che, quando ha termine ("si parte") il gioco della zara, il perdente rimane addolorato e cerca di imparare a fare meglio la prossima volta, ripassando nella memoria le cattive puntate che ha fatto, e quelle buone che non ha fatto, mentre tutti se ne vanno (naturalmente) con il vincitore, sperando di approfittare della sua euforia e della sua generosità. Fate attenzione a quella parola: « volte ». Fra Giovanni da Serravalle, traduttore della Commedia in latino e contemporaneo del Buti, così commenta in proposito:
« Quando in ludo taxillorum sunt tres taxilli, numerus punctorum vocatur "volta". Modo omnes qui habent voltas, scilicet numerus punctorum, inter septem et tria, dicuntur habere malas voltas, quia cum tribus taxillis rare veniunt sex vel quinque, et rarius quator vel tria. Eodem modo accident illis, qui habent "voltas" inter quatuordecim et decemocto, quia rare veniunt cum tribus taxillis quatuordecim, quindecuim et sexdecim, sed rarius decempseptem, dicuntur "bonae voltae", quia frequentius eveniunt (...) Completo ludo, ille qui perdit remanet tristis et dolens, recogitat suas "malas voltas" et conatur addiscere pro alia vice eligere "meliores voltas"
»
[Nel gioco dei dadi con tre dadi, il numero dei punti si chiama "volta". Tutti coloro che hanno "volte" comprese fra il sette e il tre si dice che hanno "cattive volte", perché con tre dadi raramente sortiscono il sei e il cinque, e più raramente il quattro o il tre. Lo stesso vale per quanti hanno "volte" tra il quattordici e il diciotto, perchè raramente con tre dadi escono il quattordici, il quindici e il sedici, e anche più di rado il diciassette e il diciotto. Le volte invece comprese fra il sette e il tredici si dicono "buone", perché escono più spesso (...) Finito il gioco, colui che perde rimane triste e dolente, ripensa alle "cattive volte" che gli sono toccate, e si sforza di imparare per altre occasioni a scegliere volte migliori.]
Ricapitolando, ecco come Fra Giovanni da Serravalle classifica i punti nel gioco della Zara:
Rare veniunt (sortiscono raramente):
il 5, da un dado con il 3 e due con l'1; o da due dadi con il 2 e uno con l'1 (due "volte" in tutto)
il 6, da un dado con il 4 e due con l'1; o da uno con il 3, uno con il 2, uno con l'1; o da tre dadi con il 2 (tre "volte" in tutto)
il 15, da due dadi con il 6 e uno con il 3, o da uno con il 6, uno con il 5, uno con il 4: o da tre dadi con il 5 (tre "volte" in tutto)
il 16, da un dado con il 4 e due con il 6; o da due dadi con il 5 e uno con il 6 (due "volte" in tutto)
Rarius veniunt (sortiscono ancora più raramente):
il 3, da tre dadi con l'1 (una "volta")
il 4, da un dado con il 2 e due con l'1 (una "volta")
il 17, da un dado con il 5 e due con il 6 (una "volta")
il 18, da tre dadi con il 6 (una "volta")
A questo punto si può facilmente intuire la motivazione che determinò nel gioco la regola dell'esclusione dei numeri 3, 4, 17 e 18, dal momento che qualsiasi giocatore non sprovveduto non avrebbe mai puntato su quei numeri, in quanto la semplice esperienza sulle frequenze delle terne di numeri (« repetendo le volte ») insegnava che quei numeri non potevano che sortire molto più raramente degli altri; da qui l'inutilità di considerarli parte del gioco.
Continuando con questo ragionamento puramente empirico:
il 7 poteva sortire quattro "volte": {5,1,1}; {4,2,1}; {3,3,1}; {3,2,2}
l'8 poteva sortire cinque "volte": {6,1,1}; {5,2,1}; {4,3,1}; {4,2,2}; {3,3,2}
il 9 poteva sortire sei "volte": {6,2,1}; {5,3,1}; {5,2,2}; {4,4,1}; {4,3,2}; {3,3,3}
il 10 poteva sortire sei "volte": {6,3,1}; {6,2,2}; {5,3,2}; {5,4,1}; {4,4,2}; {4,3,3}
l'11 poteva sortire sei "volte": {6,4,1}; {6,3,2}; {5,5,1}; {5,4,2}; {5,3,3}; {4,4,3}
il 12 poteva sortire sei "volte": {6,5,1}; {6,4,2}; {6,3,3}; {5,5,2}; {5,4,3}; {4,4,4}
il 13 poteva sortire cinque "volte": {6,6,1}; {6,5,2}; {6,4,3}; {5,5,3}; {5,4,4}
il 14 poteva sortire quattro "volte": {6,6,2}; {6,5,3}; {6,4,4}; {5,5,4}.
Il numero totale delle "volte" è pari a 1 + 1 + 2 + 3 + 4 + 5 + 6 + 6 + 6 + 6 + 5 + 4 + 3 + 2 + 1 + 1 = 56, numero che ritroveremo nel seguito.
![]()
Come si vede dal nostro elenco, il 9, il 10, l'11 e il 12 erano tutti ottenibili da sei "volte". Eppure, i giocatori esperti sapevano che il 10 e l'11 escono più frequentemente del 9 e del 12: come mai?
Il primo a rispondere correttamente fu Galileo, nel già citato trattato "Sulla scoperta dei dadi", scritto per risolvere proprio questo dilemma, a lui posto dal Granduca di Toscana. Al tempo di Galileo ogni puntata era ancora effettuata sulla "volta", intesa come terna costituita dai numeri dalla cui somma è possibile ottenere un numero dato; egli fu il primo a ragionare in maniera diversa. Nella sua operetta infatti esordisce così:
« Che alcuni punti nel gioco dei dadi sieno più vantaggiosi di altri, vi ha la sua ragione assai manifesta, la quale è il poter quelli più facilmente e più frequentemente scoprirsi che questi, il che dipende dal potersi formare con più sorte di numeri, onde il 3 e il 18, come punti che in un sol modo si possono con tre punti comporre. »
Analizzando tutti i possibili punteggi ottenibili con il lancio di tre dadi, il genio pisano scopre che in realtà sia il 10 che l'11 si possono ottenere in 27 modi diversi, mentre il 9 e il 12 in soli 25 modi diversi. In effetti, se vogliamo ottenere un dato numero sommando i tre che si presentano sulle tre facce dei dadi, ciascuno di questi numeri può uscire su un dado, oppure sull'altro o sull'altro ancora, purché, indipendentemente dal dado sul quale sono usciti, l'evento complessivo sia quello che siano usciti tutti e tre. Partendo da questa osservazione Galileo Galilei osserva che:
il 3 si può ottenere da un solo evento: {1,1,1}, che dà vita a una "volta" sola;
il 4 si può ottenere invece da tre eventi: {2,1,1} {1,2,1} {1,1,2}, raggruppabili in una "volta";
per il 5 gli eventi diventano sei: {3,1,1} {1,3,1} {1,1,3}, raggruppabili in una "volta", {2,2,1} {2,1,2} {1,2,2}, raggruppabili invece in un'altra, per un totale di due "volte";
al 6 danno vita ben 10 eventi: {2,2,2} (la prima "volta"), {4,1,1} {1,4,1} {1,1,4}, raggruppabili in una seconda "volta", {3,2,1} {2,1,3} {1,3,2} {1,2,3} {2,3,1} {3,1,2}, che danno vita alla terza "volta";
al 7 danno vita 15 eventi, che non stiamo ad elencare tutti, raggruppabili in quattro "volte";
all'8 danno vita 21 eventi, raggruppabili in cinque "volte";
al 9 danno vita 25 eventi, raggruppabili in sei "volte";
per il 10 si tocca il massimo: 27 eventi, che però sono raggruppabili in sei "volte", come il 9;
anche l'11 si può ottenere da 27 eventi, ma anche in questo caso da solo sei "volte";
il 12 torna ad essere ottenibile da 25 eventi, corrispondenti ancora a sei "volte";
il 13 proviene da 21 eventi, raggruppabili in cinque "volte", come l'8;
il 14 proviene da 15 eventi, raggruppabili in quattro "volte", come il 7;
il 15 proviene come il 6 da 10 eventi: {5,5,5} (la prima "volta"), {3,6,6} {6,3,6} {6,6,3}, raggruppabili in una seconda "volta", {4,5,6} {5,6,4} {6,4,5} {6,5,4} {5,4,6} {4,6,5}, che danno vita alla terza "volta";
al 16 danno vita 6 eventi: {4,6,6} {6,4,6} {6,6,4}, raggruppabili in una "volta", e {5,5,6} {5,6,5} {61,5,5}, raggruppabili invece in un'altra, per un totale di due "volte", come il 5;
al 17 danno vita solo tre eventi: {6,5,5} {5,6,5} {5,5,6}, raggruppabili in una "volta" sola, come il 4;
infine, il 18 (come il 3) proviene da un evento solo: {6,6,6}, che dà vita a una "volta" sola.
Si noti come questa tabella sia manifestamente simmetrica:

Dal momento che 10 e 11 sono ottenibili tramite 27 eventi su 216, mentre 9 e 12 tramite 25 eventi su 216, Galileo Galilei ha risolto brillantemente il problema postogli dal suo signore, confermando la previsione degli incalliti giocatori di zara!
Per parlare in termini di probabilità (intesa in senso classico) come la hanno concepita Pascal e Fermat, siccome i casi possibili totali sono 216, se ne deduce che:
3 e 18 si presentano con probabilità 1/216 = 0,46 %
4 e 17 con probabilità 3/216 = 1/72 = 1,39 %
5 e 16 con probabilità 6/216 = 1/36 = 2,78 %
6 e 15 con probabilità 10/216 = 5/108 = 4,63 %
7 e 14 con probabilità 15/216 = 5/72 = 6,94 %
8 e 13 con probabilità 21/216 = 7/72 = 9,72 %
9 e 12 con probabilità 25/216 = 11,57 %
10 e 11 con probabilità 27/216 = 1/8 = 12,5 %
Si osservi come la somma di tutte le probabilità dia 216/216 = 100 %. Si dice che lo spazio delle probabilità è normalizzato: la loro somma totale deve dare l'unità. Si consideri infatti una moneta: una volta lanciata, essa può dare solo "testa" o "croce". La probabilità che esca "testa" è 1/2 = 50 % (un caso favorevole sue due possibili). Anche la probabilità che esca "croce" è 1/2 = 50 %. La loro somma dà 2/2 = 100 %; ciò si esprime dicendo che il fatto che esca "testa o croce" è un evento certo. Al contrario, il fatto che non esca "né testa né croce" è 0/2 = 0 %: si parla in tal caso di evento impossibile. Nel nostro caso, il fatto che lanciando tre dadi si ottenga 1 (o 2, o 19, o 20) rappresenta un evento impossibile.
Continuando a ragionare in termini moderni, Galilei comprese per primo la differenza tra disposizioni e combinazioni. Prima di chiudere, vale la pena di chiarire questo punto. Si chiamano disposizioni di n oggetti a gruppi di k i gruppi che si possono formare prendendo k di quegli n oggetti, ritenendo distinti i gruppi che differiscono per l'ordine. Il loro numero si indica con la scrittura Dn,k. Ad esempio, se ho 6 lettere distinte fra loro, quante parole (anche non di senso compiuto) potrò formare, prendendo 4 di esse per volta? (tale gioco è chiamato "logogrifo") Appare evidente che le parole sono diverse a seconda dell'ordine delle lettere che le costituiscono, dunque si tratta di disposizioni, e il loro numero sarà pari a D6,4. Si può dimostrare che il numero delle permutazioni di n oggetti a gruppi di k è pari a:
Dn,k = n x ( n – 1 ) x ( n – 2 ) x ... x ( n – k + 1 )
Quindi nel nostro caso si ottiene:
D6,4 = 6 x ( 6 – 1) x ... x ( 6 – 4 + 1 ) = 6 x 5 x 4 x 3 = 360
In particolare, si dicono permutazioni di n oggetti i gruppi che si possono formare con quegli n oggetti, prendendoli tutti. Il loro numero si indica con la scrittura Pn oppure n!, che si legge "fattoriale di n" o "n fattoriale", ed è dato da:
Pn = n x (n – 1) x (n – 2) x ... x ( n – n +1 ) = n x ( n – 1 ) x ... x 3 x 2 x 1
In pratica, il fattoriale di n è pari al prodotto di tutti i numeri interi a decrescere, da n fino a 1. Ad esempio, se ho n lettere distinte fra loro, quanti anagrammi (anche non di senso compiuto) potrò formare con esse? Evidentemente:
P6 = 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720
Si dicono invece combinazioni di n oggetti a gruppi di k i gruppi che si possono formare prendendo k di quegli n oggetti, ma stavolta indipendentemente dal loro ordine. Il loro numero si indica con la scrittura Cn,k. Ad esempio, presi 6 studenti, quanti gruppi posso formare prendendo 4 di loro, allo scopo di dare vita ad un lavoro di gruppo? Appare evidente che il gruppo formato da Alex, Beatrice, Niccolò e Sara è identico a tutti gli effetti al gruppo formato da Sara, Beatrice, Niccolò e Alex, dunque si tratta di combinazioni, ed il loro numero sarà pari a C6,4. Tale numero si può anche indicare nel seguente modo:

che si legge "6 sopra 4" e prende il nome di coefficiente binomiale. Il suo valore è dato dalla seguente espressione:
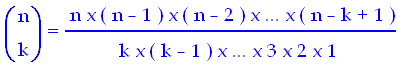
Quindi nel nostro caso si ottiene:
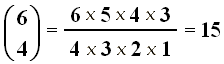
Come si può vedere, le disposizioni sono in numero sempre maggiore delle combinazioni. Ogni disposizione si ottiene dalla combinazione di quegli stessi oggetti permutandoli in tutti i modi possibili, e perciò vale la relazione fondamentale:
Dn,k = Pk x Cn,k
Si osservi che quelle che Dante Alighieri chiamava le "volte", noi le chiamiamo combinazioni, e precisamente combinazioni di 6 oggetti a gruppi di 3. Quelli che invece Galileo chiamava "eventi", noi le chiamiamo disposizioni, e precisamente disposizioni di 6 oggetti a gruppi di 3. In base alle formule sopra fornite è facile determinare D6,3 = 120, e C6,3 = 20. Come mai i conti sembrano non tornare? Perchè quelle del gioco della zara sono disposizioni e combinazioni con ripetizione. Infatti due dadi, o tutti e tre, possono presentare lo stesso punteggio, cosa che fin qui avevamo escluso. Le formule per trovare il loro numero vanno così modificate:

Se ne deduce che le disposizioni con ripetizione di 6 oggetti a gruppi di 3 sono 63 = 216, mentre le combinazioni con ripetizione di 6 oggetti a gruppi di 3 sono in numero uguale alle combinazioni senza ripetizione di 8 oggetti a gruppi di 3, cioè 56. Esattamente i totali che avevamo trovato empiricamente in quel che precede! I calcoli finiscono per confermare le previsioni dell'esperienza, in perfetto accordo con i versi di Dante da noi già citati nell'Introduzione:
« ...Solo da sensato apprende
Ciò che fa poscia d'intelletto degno! » (Par. IV, 41-42)
Per chiudere, è possibile verificare che le disposizioni e le combinazioni, sia con ripetizione sia senza, godono di una notevole proprietà di simmetria. Così, per le combinazioni senza ripetizione vale la formula:
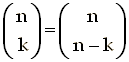
Ne consegue ad esempio che C6,4 = C6,2. Da ciò si deduce la simmetria del grafico sopra costruito da Galileo. Come si vede, nonostante le date da noi fornite sopra, il criterio della probabilità frequentista, presente in forma consapevole a tutti i giocatori di dadi, è molto più antico di Pascal, Fermat, Bernoulli, Laplace, de Finetti e Kolmogorov. E Dante, regolarmente, lo ha registrato nella sua Commedia!
E dopo l'algebra e il calcolo delle probabilità, che dire della geometria? Per avere la mia risposta a questa domanda, cliccate qui ed andiamo avanti.