Abramo "contratta" con Dio

Il nome della città palestinese di Hebron in ebraico significa "amico", e la maggioranza dei suoi abitanti arabi la chiama "al-Khalīl", dall'epiteto coranico "Khalil al-Rahman", cioè "amico del Misericordioso (quindi di Dio)", perchè in essa abitò e fu sepolto il Patriarca Abramo, che di Dio era "l'amico" per antonomasia. Il Signore infatti lo tratta con una familiarità che non riserva a nessun altro personaggio dell'Antico Testamento, nemmeno a Mosè, « con il quale il Signore parlava faccia a faccia » (Deuteronomio 34, 10). E sicuramente uno degli episodi in cui meglio si manifesta l'amicizia tra Dio e Abramo è l'episodio del loro incontro « alle Querce di Mamre, mentre egli sedeva all'ingresso della tenda nell'ora più calda del giorno », narrato nel capitolo 18 del Libro della Genesi. In quell'occasione YHWH accetta l'ospitalità di Abramo, gli promette che da lì ad un anno egli avrà un figlio da Sara, quindi svela al patriarca le sue vere intenzioni: punire duramente gli abitanti di Sodoma per il loro grave peccato. Vale la pena di rileggere l'intero brano:

« Disse allora il Signore: « Il grido contro Sodoma e Gomorra è troppo grande e il loro peccato è molto grave. Voglio scendere a vedere se proprio hanno fatto tutto il male di cui è giunto il grido fino a me; lo voglio sapere!"
Quegli uomini partirono di lì e andarono verso Sodoma, mentre Abramo stava ancora davanti al Signore. Allora Abramo gli si avvicinò e gli disse: "Davvero sterminerai il giusto con l'empio? Forse vi sono cinquanta giusti nella città: davvero li vuoi sopprimere? E non perdonerai a quel luogo per riguardo ai cinquanta giusti che vi si trovano? Lungi da te il far morire il giusto con l'empio, così che il giusto sia trattato come l'empio; lungi da te! Forse il giudice di tutta la terra non praticherà la giustizia?"
Rispose il Signore: "Se a Sodoma troverò cinquanta giusti nell'ambito della città, per riguardo a loro perdonerò a tutta la città."
Abramo riprese e disse: "Vedi come ardisco parlare al mio Signore, io che sono polvere e cenere... Forse ai cinquanta giusti ne mancheranno cinque; per questi cinque distruggerai tutta la città?" Rispose: "Non la distruggerò, se ve ne trovo quarantacinque."
Abramo riprese ancora a parlargli e disse: "Forse là se ne troveranno quaranta." Rispose: "Non lo farò, per riguardo a quei quaranta."
Riprese: "Non si adiri il mio Signore, se parlo ancora: forse là se ne troveranno trenta." Rispose: "Non lo farò, se ve ne troverò trenta."
Riprese: "Vedi come ardisco parlare al mio Signore! Forse là se ne troveranno venti." Rispose: "Non la distruggerò per riguardo a quei venti."
Riprese: "Non si adiri il mio Signore, se parlo ancora una volta sola; forse là se ne troveranno dieci." Rispose: «"Non la distruggerò per riguardo a quei dieci."
Poi il Signore, come ebbe finito di parlare con Abramo, se ne andò e Abramo ritornò alla sua abitazione. » (Gen 18, 20-33)

Come si legge, si tratta della tipica "contrattazione" orientale, in cui Abramo rilancia in continuazione, ogni volta che il Signore accetta la sua proposta, abbassando la posta fino ad un limite  che appare incredibile: dieci soli giusti per salvare un'intera città abitata da migliaia di persone! Nella sua Catechesi del 18 maggio 2011, così si esprime in proposito Papa Benedetto XVI:

« Se leggiamo attentamente il testo, ci rendiamo conto che Abramo non si limita a domandare la salvezza per gli innocenti. Abramo chiede il perdono per tutta la città e lo fa appellandosi alla giustizia di Dio; dice, infatti, al Signore: "E non perdonerai a quel luogo per riguardo ai cinquanta giusti che vi si trovano?" (18, 24b) Così facendo, mette in gioco una nuova idea di giustizia: non quella che si limita a punire i colpevoli, come fanno gli uomini, ma una giustizia diversa, divina, che cerca il bene e lo crea attraverso il perdono che trasforma il peccatore, lo converte e lo salva. Con la sua preghiera, dunque, Abramo non invoca una giustizia meramente retributiva, ma un intervento di salvezza che, tenendo conto degli innocenti, liberi dalla colpa anche gli empi, perdonandoli. Il pensiero di Abramo, che sembra quasi paradossale, si potrebbe sintetizzare così: ovviamente non si possono trattare gli innocenti come i colpevoli, questo sarebbe ingiusto, bisogna invece trattare i colpevoli come gli innocenti, mettendo in atto una giustizia "superiore", offrendo loro una possibilità di salvezza, perché se i malfattori accettano il perdono di Dio e confessano la colpa lasciandosi salvare, non continueranno più a fare il male, diventeranno anch’essi giusti, senza più necessità di essere puniti. »

Fernando Monzio Compagnoni, Lot fugge da Sodoma con le figlie

Ma l'evento intorno a cui ruota l'episodio, appartiene alla storia o al mito? Sodoma è esistita veramente, o appartiene solo al folklore ebraico, come l'isola dei Ciclopi nell'"Odissea" o l'isola di Avalon nel mito arturiano, ed è stata inserita dall'Autore Biblico nella vicenda di Abramo solo per dimostrare quanto può il giusto nella sua opera di intercessione presso l'Onnipotente? La risposta a questa domanda è ancora oggi oggetto di dibattito fra gli studiosi. Tanto per cominciare, le città peccatrici non erano due (Sodoma e Gomorra), ma ben cinque:

« [I quattro re d'oriente] mossero guerra contro Bera re di Sòdoma, Birsa re di Gomorra, Sinab re di Adma, Semeber re di Seboìm, e contro il re di Bela, cioè Zoar. » (Gen 14, 2)

Di queste cinque città una sola è citata come esistente nel prosieguo della Bibbia, e cioè l'ultima, che infatti sarebbe stata anche l'ultima a sopravvivere al disastro:

« Ma Lot gli disse: "No, mio signore! Vedi, il tuo servo ha trovato grazia ai tuoi occhi e tu hai usato grande bontà verso di me salvandomi la vita, ma io non riuscirò a fuggire sul monte, senza che la sciagura mi raggiunga e io muoia. Ecco quella città: è abbastanza vicina perché mi possa rifugiare là ed è piccola cosa! Lascia che io fugga lassù - non è una piccola cosa? - e così la mia vita sarà salva". Gli rispose: "Ecco, ti ho favorito anche in questo, di non distruggere la città di cui hai parlato. Presto, fuggi là, perché io non posso far nulla finché tu non vi sia arrivato". Perciò quella città si chiamò Zoar. » (Gen 19, 18-22)

Zoar, "Segor" nella versione dei Settanta, vuol dire infatti "piccolezza". Essa è citata anche alla fine del Pentateuco, come limite estremo delle terre mostrate da YHWH a Mosè prima che questi muoia:

« Il Signore gli mostrò tutta la terra: Gàlaad fino a Dan, tutto Nèftali, la terra di Èfraim e di Manasse, tutta la terra di Giuda fino al mare occidentale e il Negheb, il distretto della valle di Gerico, città delle palme, fino a Soar » (Dt 34, 1b-3)

Ne parla anche Isaia nel suo oracolo contro il Regno di Moab, specificando che Zoar fa parte di esso:

« Il mio cuore geme per Moab; i suoi fuggiaschi giungono fino a Zoar. » (Isaia 15, 5a)

I Moabiti abitavano lungo la costa orientale del Mar Morto, cioè nell'attuale Giordania; è da quelle parti che va localizzata Zoar e, di conseguenza, tutte le città della Pentapoli cananea. Giuseppe Flavio, nella sua "Guerra giudaica", la chiama « Zoar d'Arabia », mentre Eusebio nell'"Onomasticon" afferma che « il Mar Morto si trova fra Gerico e Zoar ». Zoar è presente nelle opere di alcuni geografi arabi sotto il nome di Zughar o Sughar, che la localizzano in un'arida vallata a sud di Gerico, definendola un'importante stazione di sosta sulla via fra Gerico e Aqaba. La posizione più plausibile per gli archeologi è alle pendici dei monti di Moab, ad est di Uadi Ghurundel, dove esiste tuttora una fertile oasi. Passiamo alle altre quattro città. Nel 1977 l'assiriologo siciliano Giovanni Pettinato (1934-2011) annunciò di aver ritrovato la lista delle "cinque città della pianura", Sodoma, Gomorra, Adma, Zeboim e Bela in una tavoletta di Ebla, la città siriana del III millennio avanti Cristo riportata alla luce da Paolo Matthiae nel 1975; in quella tavoletta i nomi delle cinque città appaiono nello stesso ordine con il quale sono contenute nella Genesi! Seboìm in ebraico significa "iene", un'etimologia che indica un posto desertico e desolato, e qualcuno ha proposto di identificarla con Talaa Sebaan, un vasto complesso di rovine fra il Mar Morto e la città di Kerak in Giordania. Adma, in ebraico 'adhmah, "rosso", rimanda al concetto di "terra rossa", e quindi ancora una volta desertica; una città con lo stesso nome è citata in Giosuè 3, 16, ma è posta a nord del Mar Morto, e quindi probabilmente si tratta solo di un'omonimia.

E le due città più famose, Sodoma e Gomorra? Secondo il mio amico glottologo professor Guido Borghi dell'Università di Genova, il nome di Sodoma / Səḏōm è privo di confronti in ebraico, e di solito viene connesso alla radice araba √s-d-m-, "essere triste", anche se il dottor Borghi ritiene che possa essere piuttosto un nome eteo (ittita) da una base indoeuropea*sed-umo-s dal significato più o meno di "sede", dalla radice √*sed- "sedersi": Sodoma infatti avrebbe potuto nascere come stazione di sosta lungo la via che dal Mar Rosso conduceva in Mesopotamia (la cosiddetta "Strada dei Re"). Invece il fatto che nella Tradizione ebraica tiberiense Gomorra fosse pronunciata Ġəmōrāh ha fatto pensare a una radice √ġ-m-r-, "essere profondo, abbondante", detto di acqua, e quindi al fatto che la città sorgesse in un'oasi; Ġəmōrāh corrisponde regolarmente a ʿªmōrāh, che però a sua volta, a parere del dottor Borghi può essere confrontato anche con la radice nabatea √ʿ-m-r-₁ "abitare" (Il nome ebraico del Re Omri [884-873], ʿŎmrī "Gomorrita", reso Ḫumri in cuneiforme, non è diagnostico al riguardo). Le cinque città sorgevano nella Valle di Siddim, la "Valle dei Boschi", della quale l'autore biblico dice: « Tutti questi si concentrarono nella valle di Siddìm, cioè del Mar Morto » (Gen 14, 3) Ma la regione del Mar Morto, come si sa, è talmente arida da risultare incompatibile con una vallata coperta di boschi e "abbondante d'acqua", come indicherebbe l'etimologia di Gomorra, tanto da farne una stazione di sosta lungo una via carovaniera, come indicherebbe invece l'etimologia di Sodoma!

Il Mar Morto visto da Google Earth

Una possibile soluzione dell'enigma è suggerita da Werner Keller (1909-1980) nel capitolo 7 del suo bestseller "La Bibbia aveva ragione" (1956). Nel 1847 il capitano William Francis Lynch (1801-1865), che in seguito si sarebbe distinto nell'esercito Confederato durante la Guerra di Secessione Americana, guidò una spedizione lungo il fiume Giordano e fu il primo occidentale ad esplorare il Mar Morto, scoprendo con sorpresa che esso occupa la fossa tettonica più profonda della crosta terrestre: il suo livello si trova 415 metri sotto il livello del mare, e il fondo addirittura tocca i meno 800 metri! « Sulla superficie di un altro pianeta potrà esistere qualcosa che somigli alla Valle del Giordano, ma sul nostro no di certo », scrisse in proposito lo scozzese George Adam Smith (1856-1942) nella sua opera "La geografia storica della Terrasanta" (1894). Il Mar Morto ha una salinità incredibile, superiore al 33 %, a causa della forte evaporazione che nei secoli ne ha abbassato il livello; ed ecco perchè oggi gli israeliani lo chiamano ים המלח‎ ("Yam HaMelah"), cioè "mare del sale". Ciò non consente alcuna forma di vita in esso, fatta eccezione per alcuni tipi di batteri, da cui deriva il nome di Mar Morto. Esso è suddiviso in due bacini distinti: quello superiore, profondo quasi 400 metri, e quello inferiore, che non ha mai superato i 2 metri di profondità massima; quest'ultimo è oggi quasi prosciugato. I due bacini sono separati dalla penisola di el-Lisan, sulla sua sponda orientale, che forma una vera e propria lingua di terra (el-Lisan in arabo significa "la lingua"). Essa è esplicitamente menzionata nella Bibbia, quando parla della suddivisione della Terra di Canaan da parte degli Ebrei:

« Il confine dei figli di Giuda a mezzogiorno cominciava dalla parte estrema del Mar Morto, dalla penisola rivolta verso mezzogiorno » (Giosuè 15, 2)

Ed ecco cosa ci racconta Werner Keller ne "La Bibbia aveva ragione":

« Remando in una barca verso la punta meridionale del mare salato col sole in posizione favorevole, si può osservare qualcosa di sbalorditivo: a una certa distanza dalla sponda, sotto lo specchio dell'acqua, si stagliano chiari i contorni di boschi conservati dall'elevatissimo contenuto di sale delle acque. I tronchi e i resti degli alberi nelle profondità verdastre devono essere antichissimi. Quando fiorivano, quando il verde fogliame ornava i loro rami, le greggi di Lot avranno forse pascolato sotto di essi. Quella parte piana, così singolare del Mar Morto, dalla penisola di el-Lisan alla punta meridionale, era la valle di Siddim! »

L'idea è dunque che, prima della catastrofe che distrusse Sodoma, Gomorra, Adma e Seboim risparmiando la sola Zoar, la zona fosse un'oasi rigogliosa e coperta di boschi. La presenza di alberi permette di edificare città senza bisogno di ricorrere a pietre o mattoni di argilla, e questo indicherebbe che la Pentapoli della Pianura sarebbe sorta proprio all'interno dell'attuale bacino inferiore del Mar Morto. La causa della distruzione sarebbe stata un catastrofico terremoto, probabilmente accompagnato da emissioni di gas e di zolfo, perchè la fossa del Mar Morto è parte di una grande Rift Valley che dai Monti del Tauro giunge fino in Africa attraversando tutto il Mar Rosso, e si sa che le fosse tettoniche sono tutte di origine ignea. Ciò che restava delle quattro città peccatrici sarebbe stato inghiottito dalla terra e quindi ricoperto dalle acque salse del Mar Morto: ecco il motivo per cui non ne è stata mai trovata alcuna evidenza archeologica (anche se nel kolossal "La Bibbia" di John Houston se ne vedono le rovine, attraverso cui passano Abramo e Isacco). Così prosegue inoltre Werner Keller:

« Ad ovest della riva meridionale del Mar Morto si stende da nord a sud un dorsale collinoso alto 45 metri e lungo 15 chilometri. Sui suoi pendii sotto la luce del sole si osserva uno sfavillio come di diamanti. È un raro fenomeno della natura: la maggior parte di questa piccola catena di alture consiste di puri cristalli di sale. Gli arabi la chiamano Gebel Usdum, nome antichissimo nel quale si è conservata la parola Sodoma. Molti blocchi di sale, lavati e staccati dalla pioggia, sono precipitati in basso. Hanno forme strane. Alcuni stanno ritti come statue. Nei loro profili sembra a volte di scorgere all'improvviso figure umane. »

Una formazione rocciosa presso il Mar Morto nota come "la Moglie di Lot"

Questa singolare caratteristica del paesaggio spiegherebbe la sorte toccata alla moglie di Lot, che « guardò indietro e divenne una statua di sale » (Gen 19, 26). Altri invece spiegano questa leggenda affermando che la donna, attardatasi, sarebbe rimasta vittima delle esalazioni venefiche del sottosuolo e sarebbe stata ricoperta dal sale scagliato in aria dal terremoto e dai fenomeni vulcanici. In ogni caso, anche ammettendo che le Città della Pianura sorgessero davvero nel bacino inferiore del Mar Morto, la questione è un'altra: quale fenomeno tellurico avrebbe potuto spianare al suolo quattro grandi città? Sebbene infatti la valle del Giordano sia parte di una fossa tettonica, non vi soo prove geologiche di eruzioni catastrofiche avvenute nell'area intorno al 1900 a.C., l'epoca cioè di Abramo. E così, qualcuno ha pensato che Sodoma e le altre città non siano mai esistite se non nella mitologia ebraica, così come le mitiche città d'oro di Cibola della leggenda spagnola, o l'Atlantide di Platone. Anzi, Sodoma rappresenterebbe l'equivalente cananeo proprio della perduta Atlantide, simbolo di una città ricca e splendida fiorita nella notte dei tempi, che fu inghiottita non dall'acqua ma dal suolo, essendo i cananei una popolazione di terraferma, nel giro di un solo giorno. In questo senso, la sua distruzione con lo zolfo e il fuoco rappresenterebbe una "saga eziologica" (volta cioè a spiegare le "cause" delle cose) con lo scopo proprio di giustificare l'aridità della regione del Mar Morto, in contrapposizione con la lussureggiante Galilea intorno al Mare di Tiberiade, attraverso un disastro causato dalla collera divina contro un popolo insolente e peccaminoso: « Il sole spuntava sulla terra e Lot era arrivato a Zoar, quand'ecco il Signore fece piovere dal cielo sopra Sòdoma e sopra Gomorra zolfo e fuoco provenienti dal Signore. Distrusse queste città e tutta la valle con tutti gli abitanti delle città e la vegetazione del suolo » (Gen 19, 23-25). Io però non sono d'accordo con tale interpretazione, e non lo è neanche Werner Keller, che nel suo libro scrive:

« La sinistra efficacia di questo racconto biblico riguardante la punizione di una peccaminosità incorreggibile ha impressionato profondamente in tutti i tempi gli animi degli uomini. Sodoma e Gomorra divennero il simbolo della depravazione e dell'empietà, e si citano i loro nomi quando si parla di una distruzione completa. La fantasia degli uomini deve aver concepito le cose più spaventose pensando a quel fatto inspiegabile... »

Insomma, come già è accaduto con il racconto del diluvio universale, si tratta di una tragedia dalle proporzioni troppo immani, per essere stata inventata di sana pianta. Un nucleo storico ci deve pur essere, alla base di esso. Ora, noi sappiamo che la valle del Giordano fu abitata fin dall'antichità più remota: la città di Gerico è abitata ininterrottamente da 11.000 anni, e molti pensano che sia la città più antica della Terra. Se davvero a sud del Mar Morto era localizzata una grande oasi, non c'è motivo per non pensare che anch'essa sia stata abitata da altrettanto tempo. Una catastrofe tettonica avvenuta nel Pleistocene (e noi sappiamo che ce ne sono state molte) può aver davvero colpito all'improvviso e inaspettatamente una comunità di cacciatori-raccoglitori appartenenti all'antica cultura Natufiana, una cultura neolitica fiorita in Palestina tra 12.500 e 10.200 anni fa e scoperta tra il 1932 e il 1942 da Dorothy Garrod (il sito natufiano di Beidha in Giordania è prossimo al Mar Morto meridionale), o a qualche cultura ancora precedente, facendole fare la fine degli abitanti di Pompei e Ercolano nel 79 d.C. Non a caso la visione di Abramo della valle sconvolta dalla catastrofe ricorda molto da vicino il racconto che Plinio il Giovane fece dell'eruzione del Vesuvio, alla quale assistette di persona:

« Abramo andò di buon mattino al luogo dove si era fermato alla presenza del Signore; contemplò dall'alto Sòdoma e Gomorra e tutta la distesa della valle e vide che un fumo saliva dalla terra, come il fumo di una fornace. » (Gen 19, 27-28)

Amplificata dai racconti orali e dal terrore reverenziale che gli uomini di ogni tempo hanno sempre provato di fronte allo scatenarsi della furia degli elementi, questa tradizione avrebbe dato vita al racconto delle città incenerite dallo zolfo celeste; successivamente, tale racconto sarebbe entrato a far parte del corpus mitologico ebraico, dopo l'arrivo degli Israeliti in Palestina. Infine, durante la deportazione a Babilonia i redattori del testo biblico, pur consci della sua antichità, avrebbero volutamente trasportato il racconto della distruzione di Sodoma all'epoca di Abramo, onde mostrare la capacità di intercessione del grande patriarca d'Israele, arrivato fino a un soffio dal salvare la città più peccatrice della Terra. E non basta: secondo alcuni, il racconto della distruzione di Sodoma è così antico da rappresentare una vera e propria "versione alternativa" del racconto del diluvio universale! Quello di Gen 6-9, per capirci, sarebbe il racconto del "diluvio con l'acqua", di origine mesopotamica (risale al mito di Gilgamesh), mentre quello di Gen 19 sarebbe il racconto del "diluvio con il fuoco", di origine palestinese. Gli esegeti che sostengono questa ipotesi mettono in evidenza molte analogie fra i due racconti leggendari. In entrambi si salva solo una famiglia: che questo in origine avvenisse anche nel mito di Sodoma lo si ricava dall'esplicita frase della figlia maggiore di Lot: « Nostro padre è vecchio e non c'è nessuno in questo territorio per unirsi a noi, come avviene dappertutto. » (Genesi 19, 31) Secondo il Talmud questa frase andrebbe spiegata supponendo che le figlie di Lot si erano ingannate ed avrebbero creduto che tutta l'umanità fosse stata sterminata dalla pioggia di zolfo e fuoco, ma la cosa appare poco credibile, dal momento che inizialmente Lot si era rifugiato a Zoar, che era scampata alla rovina per una concessione diretta dell'Onnipotente. Evidentemente il racconto iniziale prevedeva proprio che sopravvivesse una sola famiglia, quella di Lot, e le figlie si sarebbero unite al padre per permettere la preservazione della razza umana. Inoltre, non solo nel racconto del diluvio con il fuoco, ma anche nell'altro più famoso la prole avrebbe un rapporto sessuale incestuoso con il genitore: « Cam, padre di Canaan, vide la nudità di suo padre » (Genesi 9, 22) andrebbe interpretato proprio in questo senso, secondo l'antico linguaggio biblico, come afferma anche lo stesso Talmud babilonese. Dai colpevoli dell'incesto poi sarebbero nate le tribù non ebree della Palestina: da Cam, figlio di Noè, i Cananei; dalle figlie di Lot, Moabiti e Ammoniti (Moab in ebraico può essere interpretato come "nato dal padre"), le cui origini verrebbero in questo modo macchiate dal comportamento sessuale ignobile dei loro avi. Che il racconto di Sodoma e Gomorra vada interpretato in questo senso, non è certo, ma sicuramente è suggestivo!

Raffaello Sanzio, Fuga di Lot da Sodoma, Vaticano, Loggia di Raffaello

Ci siamo soffermati così a lungo sull'episodio in cui Abramo "contratta" con il suo Signore perchè il susseguirsi del numero dei giusti necessari per la salvezza di Sodoma ricorda da vicino quella che oggi noi chiamiamo progressione aritmetica. La progressione aritmetica è un particolare tipo di successione, e si definisce successione un insieme equipotente all'insieme dei numeri naturali, cioè che può essere messo in corrispondenza biunivoca con l'insieme N, eventualmente allargato allo zero. Avremo dunque un primo, un secondo, un terzo ecc. elemento della successione, che perciò indicheremo con { a₀, a₁, a₂, ... }, essendo a₀ il corrispondente di n = 0, a₁ il corrispondente di n = 1, a₂ il corrispondente di n = 2, e così via. Qualcuno la definisce anche una funzione che ha come dominio l'insieme dei numeri naturali. L'n-esimo termine della successione (a_n) viene chiamato termine generale. In genere una successione viene assegnata scrivendo la formula che esprime il termine generale in funzione di n. Ad esempio, la successione { 0, 1, 4, 9, 16... } dei quadrati può essere scritta così:

{ 0, 1, 4, 9, 16... } = { a_n = n² , n Î N }

Invece la successione { 1, 3, 4, 9, 7... } dei numeri dispari può essere scritta:

{ 1, 3, 4, 9, 7... } = { a_n = 2 n + 1 , n Î N }

Una successione più complicata è quella delle seguenti frazioni:

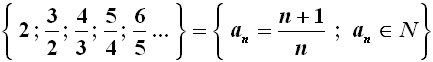
Una successione può essere anche scritta in forma ricorsiva, cioè assegnando il primo termine della successione e la formula che permette di determinare ciascun termine in funzione del precedente o dei precedenti. Un esempio è il seguente:

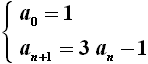
Si ha allora a₁ = 3 · 1 – 1 = 2; a₂ = 3 · 2 – 1 = 5; a₃ = 3 · 5 – 1 = 14; a₄ = 3 · 14 – 1 = 41; e così via. La successione è insomma { 1, 2, 5, 14, 41... }.

Il più famoso esempio di successione definita ricorsivamente è la cosiddetta successione di Fibonacci, ideata dal grande matematico pisano Leonardo Fibonacci (1175-1235), in cui a₁ = 1, a₂ = 1 e ogni termine è pari alla somma dei due precedenti, cioè a_n+1 = a_n + a_n–1 . I primi termini della successione di Fibonacci sono allora { 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377... }. Questa successione riveste una grande importanza, non solo in matematica; ad esempio in botanica. Nel Cantico dei Cantici infatti si dice:

« I fiori sono apparsi nei campi,
il tempo del canto è tornato
e la voce della tortora ancora si fa sentire
nella nostra campagna. » (Ct 2, 12)

Ebbene, quasi tutti i fiori hanno un numero di petali che fa parte della serie di Fibonacci. Ad esempio i gigli ne hanno tre, i ranuncoli cinque, la speronella spesso ne ha otto, la calendula tredici, l'astro ventuno, e le margherite ne hanno trentaquattro, cinquantacinque o ottantanove. Forse lo sapevano gli artisti che decorarono il Tempio di Gerusalemme, visto che « lo spessore del mare di bronzo era di un palmo; il suo orlo, fatto come l'orlo di un calice, era a forma di giglio » (1 Re 7, 26a)! Nell'infiorescenza del girasole, i piccoli fiori al centro di essa sono disposti lungo due insiemi di spirali che girano rispettivamente in senso orario e antiorario, e che seguono la successione di Fibonacci, e la stessa cosa vale per le squame legnose che compongono gli strobili, cioè le pigne, delle conifere. I numeri di Fibonacci fanno la loro comparsa anche nella moderna Teoria delle Stringhe. Infine, il limite del rapporto tra ogni numero della successione e il precedente quando n tende all'infinito è pari al rapporto aureo Φ, cioè al rapporto tra due numeri diversi tra di loro dei quali il maggiore è medio proporzionale tra il minore e la somma tra i due (Φ = 1,6180339887...). Proprio attraverso il rapporto aureo è possibile scrivere la formula generatrice dell'ennesimo termine della successione di Fibonacci, detta Formula di Binet perchè dimostrata nel 1843 dal matematico francese Jacques Philippe Marie Binet (1786-1856):

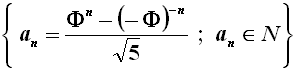
Una successione a_n si dice monotona crescente se a_n+1 è maggiore o uguale ad a_n per ogni valore di n; si dice monotona decrescente se è minore o uguale. Ad esempio, la successione dei quadrati dei numeri naturali, quella dei numeri dispari e quella di Fibonacci sono tutte monotone crescenti.

Una successione invece si dice convergente al limite finito l quando, fissato un numero reale ε > 0, piccolo a piacere, esiste in corrispondenza un n_ε tale che, per ogni n > n_ε, si abbia | a_n – l | < ε. Quest'ultima formula infatti può essere così riscritta:

l – ε < a_n < l + ε

Questo significa che, da un certo n_ε in poi, tutti i termini a_n della successione devono restare all'interno di una striscia orizzontale compresa tra le rette y = l – ε e y = l + ε, mostrata evidenziata in giallo nell'immagine seguente:

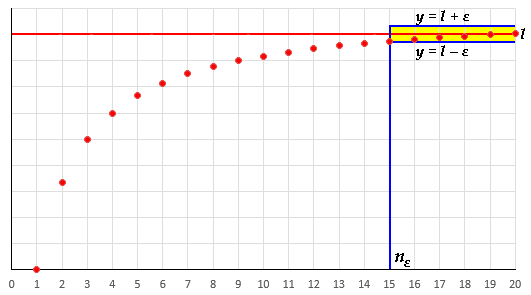
Facciamo un esempio. Sia data la succession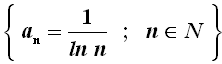e . Dimostriamo che, per n tendente all'infinito, essa tende al limite 0⁺ (cioè zero da sopra). Per quanto detto sopra, deve risultare:

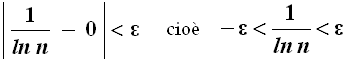
Ma 1/ln n è sempre maggiore di – ε, perchè un numero positivo è sempre maggiore di un numero negativo. Consideriamo invece 1/ln n < ε. Essa comporta che:

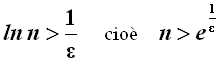
Se ε è molto piccolo, 1/ε è molto grande, ed e elevato alla 1/ε è a maggior ragione ancora più grande. Si tratta sicuramente di un numero non intero, ma basta prendere l'intero successivo e porlo uguale a n_ε per soddisfare la definizione. Infatti abbiamo dimostrato che, fissato un  piccolo a piacere, esiste in corrispondenza un valore di n tale che, per ogni numero intero maggiore di esso, il corrispondente a_n è compreso tra 0 ed ε; conclusione: al crescere di n, la successione sopra introdotta tende effettivamente al limite zero.

Al contrario diremo che una successione si dice divergente ad infinito quando, fissato un numero reale M > 0, grande a piacere, esiste in corrispondenza un n_M tale che, per ogni n > n_M, si ha | a_n | > M. In particolare, se a_n > M la successione diverge a + ∞, mentre se a_n < – M la successione diverge a – ∞. In altre parole, da un certo n_M in poi, tutti i termini a_n della successione devono restare all'interno di un angolo retto a destra della retts n = n_M e sopra la retta y = M (oppure sotto la retta y = – M), evidenziato in giallo nell'immagine seguente:

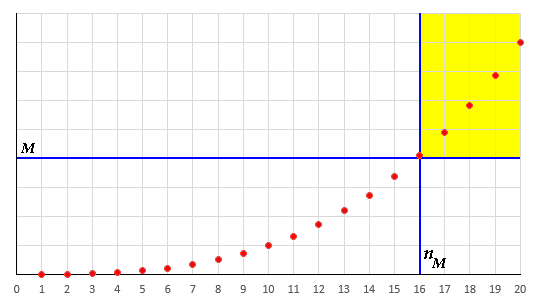
Sia ad esempio la successione . Dimostriamo che, per n tendente all'infinito, essa tende al limite + ∞. Per quanto detto sopra, deve risultare:

Se quest'ultima radice cubica è un numero decimale, basta prendere l'intero immediatamente successivo e porlo uguale a n_M. Abbiamo così dimostrato che, fissato M > 0, esiste un n_M a partire dal quale tutti i corrispondenti valori di a_n sono maggiori di + M. Più M si sposta verso l'alto, più il corrispondente n_M si sposta verso destra, e dunque la successione data non può che tendere a + ∞.

Vale poi il Teorema dell'Unicità del Limite di una Successione: il limite di una successione, se esiste, è unico. Questo teorema può essere utilizzato ad esempio per dimostrare che il limite di a_n = cos ( n π ) non esiste. Si restringa infatti tale successione ai numeri pari 2 n; il cos ( 2 n π ) è sempre pari a + 1, dunque tale sottosuccessione è costante. Restringendola invece ai numeri dispari ( 2 n + 1 ), il cos [ ( 2 n + 1 ) π ] è sempre pari a – 1. Dato che una successione non può avere due limiti distinti, se ne conclude che quella data non ne ha nessuno.

È giunto il momento di tornare all'episodio biblico da cui eravamo partiti per parlare delle successioni. L'insieme dei numeri dei giusti necessari per salvare la città di Sodoma nel capitolo 18 della Genesi, { 50, 45, 40, 30, 20, 10 }, è finito, e dunque non rappresenta una successione. Tuttavia eliminiamo il secondo degli elementi dell'insieme, quello ricavato dal versetto 28; i restanti numeri sono tali che la differenza tra ogni numero e il successivo è costante e pari a 10. Immaginiamo di estrapolare questa regola anche oltre il 10; è facile in tal modo costruire la successione { 50, 40, 30, 20, 10, 0, – 10, – 20, – 30... }. Con la notazione da noi introdotta, tale successione può essere scritta in modo ricorsivo: { a_n+1 = a_n – 10 , n Î N }.

Orbene, una successione in cui la differenza tra un termine e il precedente è costante si dice progressione aritmetica. La differenza costante tra ogni termine e il precedente si chiama ragione della progressione aritmetica, ed è indicata con la lettera d. L'ennesimo termine di una progressione aritmetica il cui primo termine è a₀ e la cui ragione è d è dato dalla semplice formula:

a_n = a₀ + n d

Infatti il primo termine è dato da a₁ = a₀ + d, il secondo termine da a₂ = a₁ + d = a₀ + 2 d, il terzo termine da a₃ = a₂ + d = a₀ + 3 d, e così via. In funzione del termine a₁, invece, la formula precedente diverrebbe:

a_n = a₁ + ( n – 1 ) d

L'esempio più semplice di progressione aritmetica è quello in cui a₁ = 1 e d = 1: è evidente che si tratta dell'insieme N dei numeri naturali. Invece la progressione in cui a₁ = 1 e d = 2 coincide con l'insieme dei numeri dispari, mentre quella in cui a₀ = 0 e d = 3 rappresenta l'insieme di tutti i multipli di 3, cioè quella che alle scuole elementari chiamavamo la "tabellina del tre"!

In molte questioni è importante conoscere la somma dei primi n termini di una progressione aritmetica. A questo proposito è utile citare un aneddoto, che forse appartiene solo alla leggenda, ma che appare molto istruttivo ai fini di ciò che stiamo studiando. Già abbiamo parlato del grande matematico Carl Friedrich Gauss (1777-1855) quando si è discusso della distribuzione gaussiana; ebbene, fin da piccolo egli si rivelò un bambino prodigio. Ebbene, secondo Wolfgang Sartorius von Waltershausen (1809-1876), discepolo e biografo di Gauss (nel 1862 pubblicò il libro "Gauss zum Gedächtnis"), quando il grande matematico aveva solo nove anni, il suo maestro elementare J.G. Büttner, che aveva bisogno di un'ora di tranquillità per svolgere un certo lavoro, ordinò ai suoi turbolenti allievi di eseguire la somma dei numeri da 1 a 100. Appena un minuto dopo però il piccolo Gauss gli portò il calcolo completo ed esatto, sbalordendolo. In effetti il nostro matematico scrisse in una riga i numeri da 1 a 100 in ordine crescente, e nella riga sottostante gli stessi numeri in ordine decrescente:

A questo punto egli si accorse che ogni colonna dà come somma 101. Sommare tutti i termini sopra scritti equivale insomma a sommare 100 volte il numero 101, e dunque per trovare la somma dei primi 100 numeri interi basterà moltiplicare 100 per 101 e dividere il risultato per 2, ottenendo 5050. Questo geniale metodo può essere generalizzato per ogni progressione aritmetica: è infatti facile accorgersi che a₁ + a_n = a₂ + a_n–1 = a₃ + a_n–2, e così via. Se ne conclude che la somma S_n dei primi n termini di una progressione aritmetica è data da:

Vogliamo ad esempio calcolare la somma dei primi 50 numeri pari a partire da 2. In questo caso a₁ = 2 e d = 2. In base a quanto abbiamo ricavato sopra si ha a₅₀ = 2 + ( 50 – 1 ) · 2 = 2 + 98 = 100, e di conseguenza avremo che S₅₀ = 50 · (2 + 100)/2 = 2550.

Proviamo a determinare, più in generale, la somma dei primi n numeri interi. Si tratta di calcolare Sn per una progressione aritmetica il cui primo termine è 1 e la cui ragione è 1; l'ennesimo termine sarà ovviamente n. Si ottiene così la semplice formula:

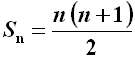
che in effetti funziona perfettamente anche nell'aneddoto riguardante l'infanzia di Gauss: per n = 100 si ha proprio S₁₀₀ = 100 · 101/2 = 5050. Proviamo invece a determinare la somma dei primi n numeri dispari a partire da n = 1. Stavolta a₁ = 1 e d = 2. Allora a_n = 1 + ( n – 1 ) · 2 = 2 n – 1. Se ne conclude che:

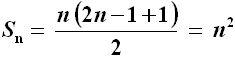
Di questa semplicissima formula esiste un'elegante dimostrazione numerica, attribuita ad Erone di Alessandria, che si può vedere illustrata nella figura sottostante:

Come si vede, aggiungendo il numero dispari di posto (n + 1) alla somma dei primi n precedenti, non si fa altro che aggiungere al quadrato una nuova riga e una nuova colonna. Quella che si vede qui sopra rappresenta la dimostrazione che la somma dei primi 6 numeri dispari è pari a 6² = 36.

Qual è il limite di una progressione aritmetica? Se d = 0, la successione è costante, e allora:

Se invece d è diverso da zero, i casi sono due: d > 0 indica una successione monotona crescente, mentre d < 0 ne indica una monotona decrescente. Appare allora evidente che una progressione aritmetica è sempre divergente, ed in particolare:

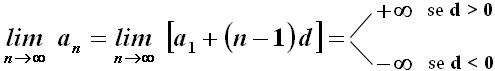
Si dice invece progressione geometrica un successione in cui il rapporto tra un termine e il precedente è costante. Tale rapporto costante si chiama anch'esso ragione, come nella progressione aritmetica, ma per distinguerla da quella di solito la si indica con la lettera q. Ovviamente la ragione deve essere diversa da zero; se q = 1, la successione è chiaramente costante, perchè tutti i termini sono pari ad a₀. Se la ragione è negativa, la successione è a termini di segno alterno. L'ennesimo termine di una progressione geometrica il cui primo termine è a₀ e la cui ragione è q è dato dalla formula:

a_n = a₀ qⁿ

Infatti il primo termine è dato da a₁ = a₀ · q, il secondo termine da a₂ = a₁ · q = a₀ · q², il terzo termine da a₃ = a₂ · q = a₀ · q³, e così via. In funzione del termine a₁, invece, la formula precedente diverrebbe:

a_n = a₁ q^n–1

A titolo di esempio si consideri la successione { 7, 21, 63, 189, 567, 1701... }: si tratta chiaramente di una progressione geometrica di primo termine 7 e di ragione q = 3. Tale successione può essere scritta in modo ricorsivo: { a₀ = 7, a_n+1 = a_n · 3 , n Î N }. Consideriamo invece la progressione geometrica in cui a₁ = 1 e q = 3: i primi termini sono { 1, 3, 9, 27, 81, 243... }, ed è facile riconoscere in essa l'insieme delle potenze di 3 maggiori di 1. Ma anche a_n = 5^n–2 è una progressione geometrica. Infatti a_n+1 = 5^n–2+1 = 5^n–1, ed è evidente che si ha a_n+1 / a_n = 5^n–1 / 5^n–2 = 5, costante. Si tratta dunque della progressione geometrica in cui a₀ = 1/25 e q = 5.

Vediamo ora se è possibile determinare la somma S_n dei primi n termini di una progressione geometrica. Essa è pari a:

S_n = a₀ + a₀ q + a₀ q² + ... + a₀ qⁿ = a₀ ( 1 + q + q² + ... + qⁿ )

Moltiplichiamo ora entrambi i membri della precedente per ( 1 – q ):

( 1 – q ) S_n = a₀ ( 1 – q ) + a₀ q ( 1 – q ) + ... + a₀ qⁿ ( 1 – q ) =

= a₀ ( 1 – q + q – q² + q² – q³ + ... + qⁿ⁺¹ ) = a₀ ( 1 – qⁿ⁺¹ )

da cui si ricava la formula:

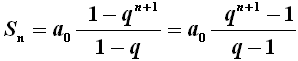
Ad esempio, la somma dei primi sei termini della progressione { 7, 21, 63, 189, 567, 1701... } sopra considerata è:

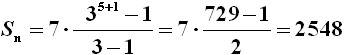
E difatti 7 + 21 + 63 + 189 + 567 + 1701 = 2548. Si noti che si è preso n = 5 perchè il primo termine ha posto zero.

Determiniamo ora il limite di una progressione geometrica per n tendente all'infinito.

a) Se q è minore o uguale a – 1, a_n cambia di segno di termine in termine al crescere di n. Il suo valore assoluto tende a + ∞, ed allora i termini pari si avvicinano a + ∞, i termini dispari a – ∞. Ne consegue che la successione non ammette limite, poiché si è visto che il limite, se esiste, è unico.

b) Se | q | < 1, cioè se – 1 < q < + 1, allora qⁿ tende a zero quando n tende all'infinito, e quindi . La successione è quindi convergente a zero.

c) Se q = 1, la progressione è costante, e dunque tende ad a₀.

d) Se infine q > 1, risulta:

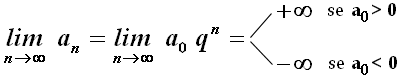
cioè la successione è divergente.

Chiediamoci ora: qual è il limite della somma degli elementi di una progressione geometrica? Si tratta di una domanda importante, perchè con essa passiamo dal concetto di successione a quello di serie. Si dice serie la somma degli infiniti termini di una certa successione. Siccome però in aritmetica non si sa come definire la somma di un numero infinito di addendi, bisogna ricorrere al formalismo dell'Analisi Matematica. Sia data dunque la successione { a₀, a₁, a₂, ... }. La serie ottenuta come somma dei suoi termini viene così scritta:

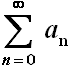
Tale somma viene definita come limite della successione delle cosiddette "somme parziali": { a₀, a₀ + a₁, a₀ + a₁ + a₂, a₀ + a₁ + a₂ + a₃, ... }. Se tale successione converge, la serie si dice convergente; se tale successione diverge, la serie si dice divergente; se tale successione non ha limite, la serie si dice indeterminata. Delle serie abbiamo parlato anche nella lezione dedicata al pi greco.

Nel nostro caso, in cui ogni addendo della serie si ottiene dal precedente moltiplicandolo per la ragione q, per trovare la sua somma occorrerà calcolare il limite per n tendente all'infinito della somma S_n dei primi n termini, vale a dire:

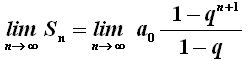
Se q è maggiore uguale a uno, questo limite tende a ∞ e la somma diverge.

Se q < 1, qⁿ tende a zero e quindi la somma converge a:

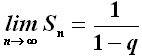
Sia ad esempio la somma della serie geometrica di primo termine 1 e ragione 1/2. Si ricava facilmente:

La somma di questa serie può essere interpretata graficamente come una somma di aree, le quali effettivamente compongono un rettangolo di area pari a 2:

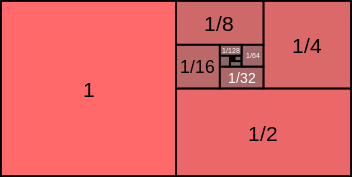
La serie geometrica ha moltissime applicazioni: permette ad esempio di trovare la frazione generatrice di un numero periodico semplice. Consideriamo il numero 0,2; esso può essere riscritto 0,222.... = 0,2 + 0,02 + 0,002 + ..., e quindi:

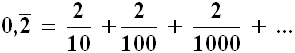
Ora, questa è una serie geometrica il cui primo termine è 2/10 e la cui ragione è q = 1/10, che è minore di 1. Se ne deduce che la serie converge al valore:

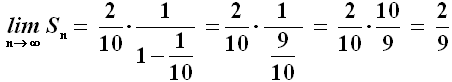
È dunque vero che la frazione generatrice di un numero periodico semplice si ottiene prendendo tutto il numero senza la virgola meno la parte intera, diviso tanti 9 quante sono le cifre del periodo!

Un'altra celeberrima applicazione della serie geometrica riguarda il cosiddetto paradosso di Achille e della Tartaruga (noto anche come paradosso di Zenone, sebbene a rigore egli abbia ideato più di un paradosso). Esso fu formulato da Zenone di Elea (489–431 a.C.), filosofo presocratico della Magna Grecia discepolo di Parmenide; Diogene Laerzio lo dice inventore della dialettica, e la sua vita si svolse ad Elea, colonia greca di Focea chiamata dai Romani Velia ed oggi nel comune di Ascea, in provincia di Salerno. Visto il tenore del nostro ipertesto, noi applicheremo il più famoso tra i paradossi di Zenone al testo biblico, sostituendo l'eroe pagano Achille con l'ebreo Asaèl, citato nel Secondo Libro di Samuele dopo la morte di Saul, quando scoppia la guerra tra coloro che sostengono Davide e coloro che invece vogliono come Re Isbaal, figlio di Saul:

« La battaglia divenne in quel giorno molto dura e furono sconfitti Abner e gli Israeliti dai servi di Davide. Vi erano là tre figli di Seruià: Ioab, Abisài e Asaèl. Asaèl era veloce nella corsa come le gazzelle della campagna. Asaèl si era messo a inseguire Abner e non deviava né a destra né a sinistra dietro ad Abner... » (2 Sam 2, 17-19)

Supponiamo dunque che, invece che con Abner, capo dell'esercito di Saul che poi lo ucciderà trapassandolo da parte a parte, come il figlio di Teti e di Peleo (morto giovane quanto lui), Asaèl decida di ingaggiare una gara di corsa con una tartaruga: dopotutto lui è veloce quanto una gazzella, simbolo di velocità, mentre la tartaruga è il simbolo vivente della lentezza (gli antichi non conoscevano il bradipo). Il campione dell'esercito di Davide però concede dieci passi di vantaggio alla tartaruga; come si vede nella figura sottostante, indichiamo con AB tale vantaggio. Supponiamo anche che Asaèl corra dieci volte più veloce della tartaruga. Mentre l'ebreo percorre i dieci passi AB, la tartaruga percorre una distanza BC pari ad un passo. Mentre Asaèl percorre il passo BC, la tartaruga percorre una distanza CD pari ad un decimo di passo. Mentre Asaèl percorre il decimo di passo CD, la tartaruga percorre una distanza DE pari ad un centesimo di passo; e così via. Ne conclude Zenone: per quanto l'atleta giudeo si affanni, la lenta tartaruga resterà sempre davanti a lui, anche se solo per una distanza infinitesimale, e quindi Asaèl non potrà mai superarla.

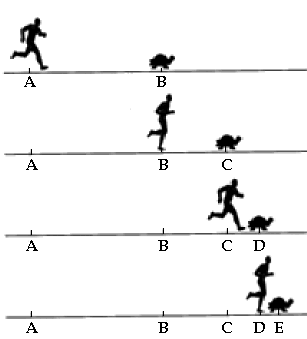
Si tratta di un evidente paradosso, che cozza contro il senso comune: il più veloce prima o poi supererà per forza il più lento. Con questo ed altri ragionamenti simili, Zenone intendeva sostenere le tesi della Scuola Eleatica, cui egli apparteneva, e dimostrare che il movimento è un'illusione. Effettivamente il paradosso è ingegnoso e affascinò molte menti geniali, tra cui quella di Jorge Luis Borges, che ne parla nelle sue "Altre inquisizioni" (1952). Tuttavia, può ingannare solo chi, a differenza dei miei lettori, non conosce l'Analisi Matematica. In effetti il ragionamento di Zenone si basa su un postulato che tutti i Greci davano per scontato: la somma di infiniti termini diversi da zero è necessariamente infinita. Per essi il concetto di "infinitesimo" e di "serie convergente" erano inammissibili. Invece, proviamo a considerare i successivi spostamenti AB, BC, CD, DE... compiuti dal nostro svelto Asaèl. Essi misurano rispettivamente dieci passi, un passo, un decimo di passo, un centesimo di passo... Perciò è immediato rendersi conto che si tratta dei termini di una serie geometrica, il cui primo termine è a₁ = 10 e la cui ragione è q = 1/10. Dato che q < 1, la serie è convergente, e precisamente converge al valore:

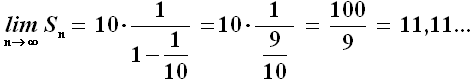
Se ne conclude che, dopo 11,11... passi, Asaèl raggiungerà la tartaruga, e da qui in poi la supererà definitivamente, dimostrando falsi gli assunti della scuola filosofica di Elea.

Vignetta raffigurante il biblico Asaèl alle prese con la tartaruga di Zenone!

Prima di chiudere questa lezione, poniamoci un'ulteriore questione. È possibile determinare il prodotto dei primi n termini di una progressione geometrica? Sì, ricorrendo ad uno stratagemma simile a quello adoperato da Gauss per la progressione aritmetica. Consideriamo infatti l'esempio già utilizzato sopra: { 7, 21, 63, 189, 567, 1701... } Si osserva che, anche in questo caso, il prodotto tra il primo e l'ultimo termine, tra il secondo e il penultimo, eccetera sono uguali tra loro: 7 · 1701 = 21 · 567 = 63 · 189 = 11.907. Scriviamo allora il prodotto dei primi n termini in questo modo:

P_n = a₁ · a₂ · a₃ · ... · a_n–2 · a_n–1 · a_n

Per la proprietà commutativa del prodotto, la precedente può essere così riscritta:

P_n = a_n · a_n–1 · a_n–2 · ... · a₃ · a₂ · a₁

Moltiplichiamo fra loro le due precedenti e adoperiamo la proprietà associativa:

P_n² = (a₁ · a_n) · (a₂ · a_n–1) · (a₃·a_n–2) · ... · (a_n–2 · a₃) · (a_n–1 · a₂) · (a_n · a₁)

Per la proprietà sopra mostrata, ognuno dei prodotti tra parentesi è pari ad a₁ · a_n; essendo n il numero di tali prodotti, allora P_n² = (a₁ · a_n)ⁿ. Quindi, estraendo la radice quadrata, otterremo il risultato finale:

Riprendiamo in considerazione di nuovo la progressione { 7, 21, 63, 189, 567, 1701... }, che ha a₁ = 7 e q = 3. Applicando la formula appena ricavata si ha:

il cui risultato è 1.688.134.559.643, cioè proprio il prodotto dei sei termini considerati!