Il mare di bronzo di Re Salomone

Pochi conoscono il versetto con cui abbiamo aperto questa lezione, eppure per i nostri scopi è di un'importanza basilare. Il settimo capitolo del Primo Libro dei Re descrive la costruzione e l'abbellimento della reggia di Re Salomone, figlio e successore di Davide, operazione che richiederà ben tredici anni. L'autore del libro riporta anche i minimi particolari del progetto: il soffitto di cedro, tre serie di finestre, il vestibolo della sala del trono, le colonne di bronzo chiamate Iachin e Boaz, i capitelli a forma di giglio, le duecento melagrane in fila intorno a ogni capitello, e poi questo « mare di bronzo », un bacile per le abluzioni poggiato su dodici buoi, tre per ogni punto cardinale. Ma attenzione: il diametro del bacile è di dieci cubiti, cioè 4,44 metri, e la sua circonferenza è di trenta cubiti, cioè 13,32 metri. Ciò significa che il rapporto tra circonferenza e diametro del bacile è pari a tre. Ma questo rapporto noi lo conosciamo bene: è quello che si indica con la lettera greca che vedete qui a fianco, e perciò lo chiamiamo tutti pi greco. Questa lettera greca fu usata per la prima volta per indicare il rapporto tra la circonferenza e il diametro di un cerchio nel 1706 nel trattato "Synopsis Palmariorum Matheseos" del matematico inglese William Jones (1675.1749): la lettera greca compare nella frase "1/2 periphery (π)", a proposito di un cerchio con raggio unitario, e Jones scelse proprio pi greco per indicare l'iniziale di periphery; ma fu il grande Eulero nel suo "Mechanica sive motus scientia analytica exposita" del 1736 a lanciare il pi greco in tutto il mondo occidentale. Eccone le prime 200 cifre decimali:

Come se non bastasse, la stessa formula è ripetuta più avanti dall'autore dei Libri delle Cronache, stavolta riferita alla vasca per le abluzioni dei sacerdoti di fronte al Tempio di Gerusalemme:

« Fece la vasca di metallo fuso del diametro di dieci cubiti, rotonda, alta cinque cubiti; ci voleva una corda di trenta cubiti per cingerla. » (2 Cronache 4,2)

Da questi due versetti ricaviamo la notizia per cui nel mondo ebraico si dava a pi greco il non precisissimo valore di 3. Ma la storia millenaria di questo numero comincia molto prima di Salomone. In Mesopotamia (terra da cui Abramo proveniva) e proprio all'epoca di Abramo, verso il 2000 a.C., erano già disponibili ampie conoscenze matematiche. In particolare nella terra tra i due fiumi era stato trovato per π il valore di 25/8 = 3,125, con un errore solo dello 0,53 %; il valore 3 desumibile dalla Bibbia è invece affetto da un errore del 4,7 %. A difesa del passo biblico si può far notare che gli Ebrei non furono mai dei maestri di ingegneria (lo stesso Tempio del Signore fu costruito da Chiram, artefice di Tiro), e per loro un'elevata precisione nelle misure era ritenuta superflua.

Un frammento del Papiro di Rhind

Nel "Papiro di Rhind", opera dello scriba egiziano Ahmes e risalente al 1650 a.C. circa (ma forse copia di un testo più antico), si attribuisce a π il valore di (16/9)² = 3,16049..., con un errore appena dello 0,6 %, anche se una sola cifra decimale era corretta. Il primo calcolo teorico preciso risale però al greco Archimede di Siracusa (287-212 a.C.), che ottenne la seguente approssimazione:

223/71 < π < 22/7

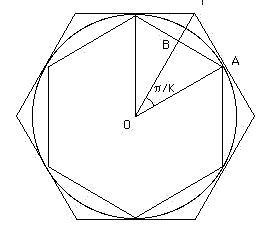
Notiamo che Archimede, a differenza dell'autore del Papiro di Rhind, aveva capito che π non vale né 223/71 né 22/7, e non fece alcun tentativo per calcolarne l'esatto valore, a differenza di tanti matematici venuti dopo di lui, e con ben altri strumenti di calcolo a disposizione. Se prendiamo come valore di π il valore medio dell'intervallo archimedeo, otteniamo 3,1418, con un errore di appena 66 parti per milione. Ecco il ragionamento di Archimede. Consideriamo un cerchio di raggio 1, in cui inscriviamo un poligono regolare di 3 x 2^n–1 lati, ed a cui circoscriviamo un poligono regolare di 3 x 2^n–1 lati, i cui semiperimetri siano rispettivamente b_n ed a_n. Il risultato è il diagramma a sinistra.

Si ottiene così una successione crescente b₁, b₂, b₃.. ed una decrescente a₁, a₂, a₃... Entrambe queste successioni hanno come limite il nostro π.

Usando la notazione trigonometrica moderna si ha che i semiperimetri sono dati da:

a_n = K tg (π/K)  ,  b_n = K sen (π/K)

dove K = 3 x 2^n-1 (vedi figura). Ragionando analogamente, si ha:

a_n+1 = 2K tg (π/2K)  ,  b_n+1 = 2K sen (π/2K)

(1/a_n + 1/b_n) = 2/a_n+1

a_n+1 b_n = (b_n+1)²

/3) = 33 e b₁ = 3 sen (

/3) = 33/2, calcolò il valore di a₂ usando la prima e di b₂ usando la seconda delle precedenti; trovò poi quello di a₃ usando la prima, poi quello di b₃ usando la seconda, e così via fino a trovare a₆ e b₆. La conclusione che egli trasse fu che:

b₆ < π < a₆

In Cina intanto il matematico ed astronomo Zu Chongzhi (430-501 d.C.) propose di usare il valore 355/113 = 3,14159292..., con un errore di sole 85 parti per miliardo! Durante il Medioevo e il Rinascimento, usando lo stesso metodo di Archimede, e giungendo fino ai poligoni con 10³⁰ lati grazie al perfezionamento dell'arte del calcolo avvenuto in seguito all'introduzione della notazione decimale, molti matematici ne affinarono i risultati: il persiano al-Kashi (1380-1429) calcolò 14 cifre decimali esatte di π, il fiammingo Adriaan van Roomen (1561-1615) arrivò a 17 decimali e il tedesco Ludolph Van Ceulen (1540-1610) si spinse addirittura a 35 cifre. Quest'ultimo fu così orgoglioso di questo risultato, che volle che fosse inciso sulla sua pietra tombale, come si vede qui sotto, e in Germania il pi greco è noto anche come Numero di Ludolph, grazie al suo exploit.

Una riproduzione della pietra
tombale di Ludolph Van Ceulen

Nel frattempo veniva scoperto un numero via via crescente di formule che nulla hanno a che vedere con la circonferenza, ma nelle quali il π compare come protagonista assoluto, e che oggi possiamo utilizzare per il calcolo delle sue cifre, in modo molto più preciso e rapido del metodo sopra esposto di Archimede. La prima è attribuita al matematico e astronomo scozzese James Gregory (1638-1675), ma fu pubblicata per la prima volta nel 1674 dal ben più famoso Gottfried Wilhelm von Leibniz (1646- 1716):

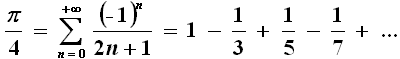
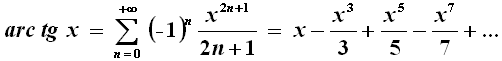
Ponendo in essa x = 1, e ricordando che arc tg 1 = π/4, si ricava immediatamente la serie di Gregory-Leibniz. Purtroppo però quest'ultima è inutilizzabile per il calcolo diretto di pi greco: infatti la sua convergenza è lentissima, e occorre sommare oltre 600 termini solo per ottenere la seconda cifra decimale esatta di π, cioè 4.

Un'altra semplicissima formula che, pur non avendo apparentemente niente in comune con la circonferenza, permette il calcolo diretto di π è la cosiddetta Serie di Eulero, intitolata al grande Leonhard Euler (1707-1783):

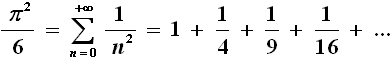
La dimostrazione della formula di Eulero è molto più complessa della precedente, ma è così intelligente che vale la pena di riportarla qui.

Essenzialmente egli suppose che le regole dei polinomi finiti fossero valide anche per le serie infinite. Naturalmente il ragionamento originale di Eulero richiede una dimostrazione di questo, ma anche senza giustificazione, semplicemente ottenendo un valore prossimo a quello ottenuto col calcolo, egli poteva essere piuttosto sicuro della correttezza del suo risultato. Eulero parte dallo sviluppo in serie di McLaurin della funzione sen x:

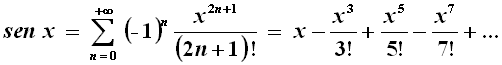
Dividendo per x entrambi i termini, egli ottiene:

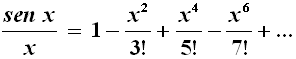
Le radici del polinomio a secondo membro sono π, 2π, 3π..., perchè sono i valori che annullano il primo membro. Poniamo ora in essa la radice quadrata di x al posto di x e la riscriviamo così:

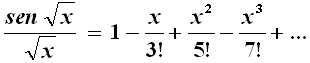
Le radici di questo polinomio sono necessariamente π², 4π², 9π²... Ora, il matematico francese François Viète (1540-1603) ha dimostrato che, se un polinomio ha il termine costante uguale a 1, la somma dei reciproci delle sue radici è uguale al coefficiente del termine lineare cambiato di segno; in altre parole la somma degli inversi delle radici del polinomio a_n xⁿ + ... + a₃ x³ + a₂ x² + b x + 1 dà come risultato ( – b). Questo è vero per polinomi con un numero finito di termini. Ma ecco il colpo di genio di Eulero, il quale suppose di poter prolungare le regole dei polinomi finiti anche a quelli infiniti, prolungamento che comunque fu dimostrato possibile molti anni dopo la sua morte. Ottenne allora, per quanto appena detto:

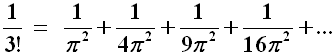
Moltiplicando entrambi i termini per π² , e ricordando che 3! = 6, si ha:

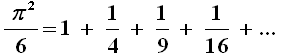
che è esattamente quanto volevamo dimostrare! Con procedimenti analoghi Eulero ottenne altre formule dello stesso genere, come ad esempio questa:

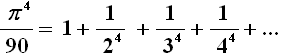
Ricostruzione del "mare di bronzo" di Re Salomone
con sovrapposta la celeberrima Formula di Eulero

Anche le formule di Eulero però, per quanto siano eleganti, hanno una convergenza assai lenta. Una serie che converge molto più rapidamente di quelle ora viste è la cosiddetta Serie di Nilakantha, intitolata al matematico e astronomo indiano Nilakantha Somayaji (1444-1544). Per utilizzarla, dopo il 3 iniziale, bisogna alternare somme e sottrazioni di frazioni il cui numeratore è 4 e il cui denominatore è il prodotto di tre numeri interi consecutivi, il primo dei quali è l'ultimo della terna precedente:

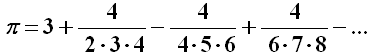
Altre formule ricorrono non a sommatorie ma produttorie infinite, come la formula di Viète:

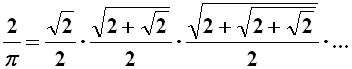
Anche Eulero trovò una produttoria che mostra una sorprendente connessione fra π e i numeri primi:

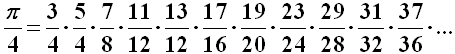
dove al numeratore vi sono tutti i numeri primi dispari e al denominatore il multiplo di quattro più vicino al numeratore. Anche questa formula è però di convergenza molto lenta: un programma da me scritto ha permesso di accertare che con 1.000 fattori si arriva al risultato 3,1458… (errore dello 0,134 %, ma solo due cifre decimali corrette), con 10.000 fattori a 3,1424… (errore dello 0,026 %, ma sempre due soli decimali) e con 100.000 termini a 3,1417… (errore di 34 parti per milione, ma appena tre decimali), quindi essa non ci porterà molto lontano, nella corsa ai decimali di π.

Vi sono formule con una convergenza parecchio più rapida, ma assai più complesse da scrivere e da adoperare. Come esempio riportiamo la "miracolosa" formula ideata dall'indiano Srinivasa Aiyangar Ramanujan (1887-1920), uno dei più grandi matematici dell'Era Moderna (sulla sua vita è stato girato nel 2015 il film "L'uomo che vide l'infinito" di Matthew Brown), che aveva l'incredibile capacità di elaborare, spesso a mente, formule complicatissime da scrivere ma comodissime da usare:

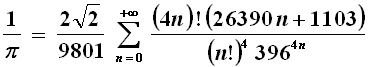
Sembra davvero un arzigogolo rispetto alle bellissime formule di Eulero, eppure già per n = 2 essa fornisce più di venti cifre decimali esatte di π, e per ogni termine sommato alla serie si ottengono cento cifre corrette in più! Un'altra formula "terrificante" ma dalla convergenza ultrarapida fu trovata nel 1987 dai fratelli David (1947-) e Grigorij Čudnovskij (1952-), matematici statunitensi di origine ucraina, noti per aver battuto a più riprese il record di calcolo di cifre pi greco con un supercomputer costruito da loro stessi nel loro appartamento di Manhattan:

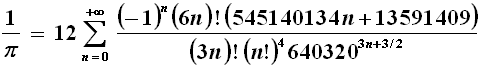
A chi gli chiedeva cosa trovassero di tanto interessante nel pi greco lui e suo fratello, David Čudnovskij rispose: « Esplorare il pi greco è come esplorare l'universo! » Ma non basta. Nel 1997 i matematici David Bailey (1948-), Peter Borwein (1953-) e Simon Plouffe (1956-) pubblicarono sulla rivista "Mathematics of Computation", una formula "magica" detta Formula BBP dalle iniziali degli scopritori, in grado di fornire l'algoritmo per calcolare una qualsiasi cifra decimale di pi greco, senza bisogno di dover calcolare tutte le precedenti:

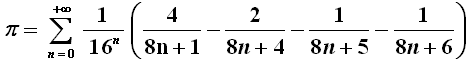
Il francese Fabrice Bellard (1972-) ne ha successivamente trovato una variante ancora più veloce. Potete provare voi stessi la convergenza di alcune di queste serie, andando a questo link (per il quale ringrazio l'amico Nicola Salucci) e decidendo voi stessi il numero di iterazioni, cioè il numero dei termini della serie che volete sommare!

Ritorniamo alla nostra breve storia dei decimali di pi greco. Il matematico e astronomo inglese Abraham Sharp (1653-1742) fu il primo ad usare la somma dei termini di una serie, da lui stesso ricavata:

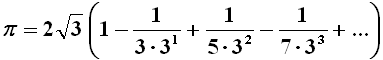
ma in realtà dovuta al matematico indiano Madhava di Sangamagrama (1350-1425), da alcuni considerato il vero fondatore dell'analisi matematica. Con questo metodo, nel 1699 Sharp si spinse fino a 71 cifre decimali, un record straordinario per i tempi. Nel 1706, John Machin (1680-1751) usò un'altra serie da lui scoperta per sfondare il muro delle 100 cifre decimali. Nel 1789 lo sloveno Jurij Bartolomej Vega (1754-1802) toccò le 126 cifre e le portò a 136 nel 1794, usando la formula da lui stesso ricavata attraverso i numeri complessi in forma trigonometrica:

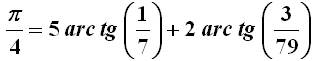
Nel 1873, William Shanks (1812-1882) calcolò (a mano!) la bellezza di 707 cifre, di cui però solo 527 esatte; considerando che egli non aveva a disposizione nessun calcolatore digitale, la sua impresa oggi ci appare titanica. Egli aveva l’hobby di calcolare costanti matematiche: ogni mattina calcolava una nuova cifra, e passava poi il pomeriggio a controllare l'esattezza del risultato. Qui sotto potete vedere la famosa Pi Shrine, una lastra di ottone con incise le prime cento cifre di π che si trova nella Public Plaza dell'Exploratorium di San Francisco.

Ma perché tanto accanimento per un calcolo del genere? Dopotutto, dieci cifre decimali di π sono già sufficienti a determinare il raggio terrestre con la precisione di un millimetro! « La matematica e il modo perfetto per prendersi in giro », ha dichiarato Albert Einstein, ma in questo caso lo sforzo dei matematici aveva uno scopo ben preciso: determinare un'eventuale ripetizione delle cifre decimali di pi greco, così da dimostrare che si tratta di un numero periodico, e quindi razionale, dotato di frazione generatrice. Tanto sforzo intellettuale apparve però inutile dopo che, nel 1766, il matematico svizzero Johann Heinrich Lambert (1728-1777), utilizzando risultati ottenuti da Eulero, dimostrò infine che π è un numero irrazionale. Questo significava che il suo valore decimale esatto era impossibile da determinarsi. La ricerca dei decimali di pi greco tuttavia continuò alla ricerca di qualche altro tipo di regolarità delle sue cifre decimali, che permettesse di metterlo in relazione con altri numeri decimali noti, ad esempio con la radice di due. Infatti non era ancora stato risolto il secolare problema della quadratura del cerchio, cioè la costruzione con riga e compasso di un quadrato avente la stessa area di un cerchio assegnato. La difficoltà titanica di risolvere questo problema, vecchio come la matematica stessa, è ben rappresentato da Dante Alighieri nell'ultimo canto della sua "Divina Commedia", quando paragona la sua incapacità di comprendere il mistero della Santissima Trinità con quella dei matematici di individuare il pi greco, definito il « principio » di cui egli indige, cioè manca:

« Qual è 'l geomètra che tutto s'affige
per misurar lo cerchio, e non ritrova,
pensando, quel principio ond'elli indige,
tal era io a quella vista nova... » (Paradiso XXXIII, 133-136)

Anche su questo problema (come quello della duplicazione del cubo, di cui abbiamo parlato in un'altra lezione) mise però la pietra tombale il tedesco Carl Louis Ferdinand von Lindemann (1852-1939), il quale nel 1882 dimostrò che pi greco è un numero irrazionale trascendente, come la base e dei logaritmi naturali e il seno di un radiante, cioè non è soluzione di alcuna equazione polinomiale a coefficienti interi. E i numeri trascendenti non possono essere costruiti con riga e compasso.

Nel 1873, infatti, Charles Hermite (1822-1901) aveva ideato una tecnica ingegnosa per dimostrare che e, la base dei logaritmi naturali, è un numero trascendente: questo fu il primo numero ad essere dimostrato con certezza come trascendente. Tale dimostrazione permise a von Lindemann di estendere nove anni dopo la tecnica di Hermite per dimostrare che anche π è trascendente: egli provò che il numero e^x è trascendente ogni volta che x è un numero algebrico non nullo; o, se si preferisce, che se e^x è algebrico, allora x o è pari a zero o ad un numero trascendente. Per dimostrare che anche π è trascendente, Lindemann si è avvalso di quella che molti considerano la "formula più bella di tutta la matematica", l'identità di Eulero:

e^iπ = – 1

Poiché – 1 è algebrico, il teorema di Lindemann afferma che iπ è trascendente. E poiché i è algebrico, π deve essere trascendente. Geniale, no? Nel 1929 il matematico russo Aleksandr Osipovič Gel'fond (1906-1968) e il tedesco Carl Ludwig Siegel (1896-1981) dimostrarono con un procedimento analogo che 2^√2 è trascendente. Quando x è algebrico il suo logaritmo dev'essere trascendente, perché e^{ln x} è uguale a x. E devono essere trascendenti anche sen x e cos x, per la nota formula di Eulero che lega e^x alla loro somma. Nel 1872 Georg Cantor (1845-1918) aveva già dimostrato che i numeri reali sono "quasi tutti" tra-scendenti, nel senso che la stragrande maggioranza di essi non è soluzione di un'equazione algebrica a coefficienti interi. In altri termini, la probabilità che un numero reale scelto a caso sia trascendente è praticamente 1. E ciò nonostante la maggior parte dei numeri scoperti e studiati dalla matematica di base siano invece algebrici: i numeri razionali, le radici n-esime dei numeri interi, le misure costruibili con riga e compasso, e così via. Il fatto è che i numeri trascendenti, pur essendo così numerosi, sono per loro natura difficili da trovare. Si pensi che il primo esempio in assoluto di numero trascendente fu scritto solo nel 1844 dal matematico francese Joseph Liouville, ed oggi è chiamata la costante di Liouville L:

L = 0,1100010000000000000000010...

Esso contiene solo 0 e 1, con gli 1 che si trovano nei posti corrispondenti ai valori di n! (n fattoriale). Quindi il primo 1 è nel primo (1!) posto, il secondo è nel secondo (2!) posto, il terzo è nel sesto (3!) posto, il quarto è nel ventiquattresimo (4!) posto, e così via. Si noti che, grazie alla sua attenta costruzione, 1/10, 11/100 e 110.001/1.000.000 sono tutte ottime approssimazioni di L, migliori di quanto ci si aspetterebbe data la dimensione dei loro denominatori. Per esempio, il terzo di questi valori ha sei (3!) cifre decimali, 0,110001, ma coincide con L per un totale di 23 cifre, ovvero 4! – 1.

Sui numeri trascendenti inoltre vi sono ancora molti problemi aperti: ad esempio si ignora se e x π, e + π, e^e, π^π e π^e siano algebrici o trascendenti, o anche solo irrazionali. Sicuramente i primi due non possono essere entrambi razionali, perché sono i coefficienti dell'equazione di secondo grado (x - e)(x - π), che ha e e π come soluzioni: dunque, almeno uno dei due è irrazionale, ma non si sa se lo siano entrambi. Tutti questi problemi, e molti altri, verrebbero risolti se si dimostrasse una congettura proposta nei primi anni sessanta dal matematico americano Stephen H. Schanuel (1933-2014), che riguarda gli omomorfismi, nell'ambito della Teoria dei Campi. Se tale congettura venisse dimostrata, e x π, e + π e π^e sarebbero trascendenti, come ci si aspetta, e la formula di Eulero sopra riportata sarebbe l'unica relazione esistente tra i numeri e, π e i esprimibile in forma algebrica mediante le operazioni di somma, prodotto ed esponenziale; ma per ora purtroppo la congettura di Schanuel sembra fuori dalla portata dei metodi matematici a nostra disposizione, per cui "l'oceano" dei numeri trascendenti resta a tutt'oggi ampiamente inesplorato. 

In ogni caso, la dimostrazione di Lindemann mise fine all'era dei matematici prodigio in grado di calcolare a mano centinaia di cifre di π, e la corsa ai decimali misteriosi ricominciò solo alla metà del XX secolo, quando l'invenzione dei calcolatori elettronici ad alta velocità fornì nuovi mezzi per la loro determinazione. A questo punto, si trattava solo di una mera sfida tra programmatori di computer a chi riusciva ad arrivare più lontano. Nel settembre del 1949 l'ENIAC, uno dei primi calcolatori elettronici messo a punto ad Aberdeen (Maryland), determinò 2036 cifre decimali in 70 ore di lavoro (Shanks per il suo calcolo aveva impiegato anni!). Nel 1954 il calcolatore NORC del Watson Scientific Laboratory di New York programmato da John von Neumann (1903-1957) sfornò 3093 cifre decimali, e in cinque anni la velocità di calcolo era talmente cresciuta, che la macchina impiegò solo 13 minuti per completare la sua impresa. Nel 1959, a Parigi, un computer IBM 704 toccò quota 10.000 decimali in un'ora e quaranta minuti di lavoro. Nel 1961 John Wrench (1911-2009) e Daniel Shanks (1917-1996, nessuna parentela con William Shanks) arrivarono a 100.265 cifre in 8 ore e 43 minuti con un IBM 7090. Nel 1973 Jean Guilloud e Martin Bouyer infransero la barriera del milione di cifre, calcolate in 23 ore e 18 minuti con il computer CDC 7600. Nell'agosto 1989 i già nominati fratelli Chudnovsky superarono il miliardo di cifre con un IBM 3090. Nel 2002 il giapponese Yasumasa Kanada (1949-), già detentore di diversi record, si issò fino a 1241 miliardi di cifre in 600 ore con un Hitachi SR8000/MPP. Il 31 dicembre 2009 Fabrice Bellard, lui pure già citato, giunse quasi a 3.000 miliardi di cifre in 121 giorni di calcolo utilizzando un computer domestico, e il 2 agosto 2010 il giapponese Shigeru Kondo (1955-) si è inerpicato sino a 5.000 miliardi di cifre in 90 giorni di calcolo, utilizzando un computer domestico modificato e sfruttando un nuovo algoritmo sviluppato da Alexander Yee (1988-), studente all'Università dell'Illinois di Urbana-Champaign. Il procedimento di quest'ultimo permise, il 13 giugno 2022, di arrivare al record attuale, 100.000 miliardi di cifre, in 157 giorni, 23 ore, 31 minuti e 7,651 secondi di lavoro, che appartiene all'informatica Emma Haruka Iwao e ai suoi colleghi di Mountain View che già nel 2019 avevano stabilito un nuovo record con 31.400 miliardi di cifre, utilizzando Google Cloud. Ma è prevedibile che entro poco tempo questo elenco dovrà essere aggiornato, se è vero che, come ha scritto Ivars Peterson, « calcolare le cifre di pi greco è lo stress test finale per un computer: una sorta di cardiogramma digitale »!

Il Guinness Book of Records registra anche il record mondiale di cifre del pi greco citate a memoria: la bellezza di 67.890, record che appartiene al ventiquattrenne cinese Lu Chao, che lo ha stabilito il 20 novembre 2005. Per declamare questa poesia matematica ci ha messo 24 ore e 4 minuti, e per impararla ha impiegato circa un anno. Sembra che un giapponese di 69 anni, Akira Haraguchi, nel 2006 sia arrivato a 100.000 cifre, ma il Guinness World Records non ha ancora omologato questo potenziale primato.

In realtà la corsa ai decimali di π non è solo una mera gara a braccio di ferro tra computer e programmatori, perchè lo studio di queste cifre potrebbe aiutarci a risolvere alcune questioni ancora aperte sul pi greco. Ad esempio, esso è o meno normale? In altre parole, la frequenza con cui è presente ogni sequenza di cifre è la stessa che ci si aspetterebbe se le cifre fossero completamente casuali? A dir la verità, non sappiamo nemmeno quale delle cifre da 0 a 9 ricorre infinite volte nell'espansione decimale di π, benché sia stato dimostrato che almeno due cifre devono ricorrere infinite volte, poiché in caso contrario pi greco sarebbe razionale, mentre oggi sappiamo che non lo è.

Per sorridere un po'...

Il π ricorre anche nella Teoria dei Numeri e nella Statistica. Come esempio si può portare l'integrale di Gauss, che è fondamentale nella cosiddetta distribuzione normale o gaussiana, ben nota al Calcolo delle Probabilità:

Inoltre la probabilità che due interi scelti a caso siano primi fra loro è pari a 6/π² (circa il 60,8 %), mentre il numero medio di modi in cui è possibile scrivere un intero positivo come somma di due quadrati perfetti è esattamente pari a π/4 = 0,785...

Vale la pena anche di raccontare il celebre metodo per stimare pi greco ideato nel 1777 dal grande scienziato francese George Louis Leclerc, conte di Buffon (1707-1788). Mentre questi lavorava, sua moglie Marie-Françoise de Saint-Belin Malain gli faceva compagnia e cuciva, e Buffon notò che ogni tanto l'ago le sfuggiva e le cadeva sul parquet. A Buffon venne allora in mente di calcolare qual era la probabilità che l'ago intersecasse le linee parallele del parquet. Detta L la lunghezza dell'ago e d la distanza costante tra le linee parallele, la probabilità P calcolata da Buffon risultò pari a 2 L/π d. Il grande uomo di scienza ebbe l'intelligenza di comprendere che questo metodo poteva venire sfruttato per la prima misura sperimentale di pi greco che non coinvolgesse in alcun modo la circonferenza: si getta un numero grandissimo di volte l'ago sul parquet, si misura la frequenza con cui l'ago interseca le linee, la si pone uguale alla probabilità P e da qui si ricava π = 2 L/P d. Nel 1901 il matematico Mario Lazzarini riuscì a valutare π tramite 3408 lanci. La curiosità consiste nel risultato a cui giunse, cioè π = 355/113, lo stesso valore indicato 14 secoli prima da Zu Chongzhi!

Siccome non è immediato ricordare i decimali di pi greco, qualcuno usa al suo posto delle approssimazioni numeriche: il già citato 22/7 di Archimede, il 355/113 di Zu Chongzhi, la somma della radice di 2 e della radice di 3, pari a 3,14626... (errore dello 0,15 %), la radice cubica di 31 = 3,14138... (errore di 67 parti per milione), la radice quadrata di 227/23 = 3,1415864... (errore di sole 2 parti per milione), la radice sesta di 17305/18 = 3,1415925... (l'errore è di appena 53 parti per miliardo); e via discorrendo. Tutte queste approssimazioni sono alla base delle rettificazioni approssimate della circonferenza con riga e compasso, di cui qui non tratteremo (se ne può vedere una in questa pagina). In alternativa, esiste un metodo mnemonico ideato negli USA per poter ricordare le prime cifre di π quando ancora non esistevano le calcolatrici tascabili. Ogni cifra successiva è data dal numero di lettere di ogni parola della seguente tiritera: « How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics. All of thy geometry, Herr Planck, is fairly hard... », da cui si ricava 3,14159265358979323846264... C'è anche un equivalente italiano, anche se più breve: « Che n'ebbe d’utile Archimede da ustori vetri sua somma scoperta? » E qualcuno ha provato perfino a convertire le cifre di π in una sequenza musicale! Oppure ancora, si può usare lo sbrigativo metodo adoperato dallo stato dell’Indiana, che con il progetto di legge 246 del 1897, passato alla storia come Indiana Pi Bill, tentò di fissare per legge il valore di pi greco a 3,2. Proposto dal deputato dell’Indiana Taylor I. Record, il progetto non divenne mai legge grazie all’intervento, del matematico della Purdue University Clarence Abiathar Waldo (1852-1926)!

Una torta per festeggiare il Pi Day!

Esiste anche il cosiddetto "Pi Day", festeggiato ogni 14 marzo, perchè questa data in inglese (March 14th) si scrive 3/14. Per la prima volta il Pi Day fu festeggiato il 14 marzo 1988 all'Exploratorium di San Francisco, per iniziativa di Larry Shaw e Jim Horton. Da allora la ricorrenza si è diffusa ovunque, e il Congresso degli Stati Uniti nel 2009 ha istituito ufficialmente il National Pi Day. Il mese di marzo del 2014 è stato salutato da qualcuno come "il Mese del Pi", a causa del fatto che si trattava del marzo (3) del 2014 (14), e il Pi Day del 2015 è stato chiamato "The Ultimate Pi Day", perchè le prime nove cifre decimali di Pi Greco sono 3,141592653, e ad esso possono essere fatti corrispondere il giorno 3/14/15 e le ore 9:26:53, secondo la notazione americana! Il Pi Day è il compleanno, guarda caso, di Albert Einstein, nato a Ulm il 14 marzo 1879, ma in questa data hanno visto la luce anche l'imperatrice bizantina Teodora (497-548), il fisico olandese Pieter van Musschenbroek (1692-1761), il chimico e farmacista italiano Giovanni Battista Schiapparelli (1795-1863), Re Vittorio Emanuele II di Savoia (1820-1878), suo figlio Umberto I (1844-1900), il biologo e geografo russo Lev Semënovič Berg (1876-1950), il matematico polacco Wacław Sierpiński (1882-1969), l'astronomo e matematico tedesco Karl Wilhelm Lorenz (1886-1918), il tenore italiano Franco Lo Giudice (1893-1990), il filosofo francese Raymond Aron (1905-1983), il fisico statunitense Robert Serber (1905-1977), l'attore e regista italiano Giancarlo Sbragia (1926-1994), il fisico italiano Emilio Zavattini (1927-2007), l'astronauta statunitense Frank Borman (1928-2023), l'attore britannico Michael Caine (1933-), l'arcivescovo di Milano cardinal Dionigi Tettamanzi (1934-2016), il fisico e matematico britannico Michael Berry (1941-), l'attore statunitense Billy Crystal (1948-), il principe Alberto II di Monaco (1958-), la cantante italiana Rita Forte (1962-), l'attore italiano Michele Riondino (1979-) e l'attore britannico Jamie Bell (1986-). Qualcuno li chiama i Viπ (Very Important Pi)! Come se non bastasse, il 14 marzo 1994 Linus Torvalds (1969-) ha presentato all'Università di Helsinki la versione 1.0.0 di Linux, la prima stabile!

Qualche matematico festeggia invece il 22 luglio, ossia il Pi Approximation Day, per il fatto che la frazione 22/7 è una comune approssimazione per eccesso di pi greco trovata per la prima volta da Archimede (per quanto ne sappiamo). Altri, ancora più bizzarri, festeggiano il 26 aprile (il 25 aprile negli anni bisestili) perchè in tale data, partendo dal 1 gennaio, la Terra percorre un arco di circonferenza pari a 2 radianti, equivalente a 1⁄π volte l'orbita totale intorno al Sole; oppure il 10 novembre (il 9 novembre negli anni bisestili), 314º giorno dell'anno secondo il calendario gregoriano. E c'è anche chi dice che, poiché π equivale a 3,141592653..., ogni giorno c'è un Pi Instant, che corrisponde alle ore 3:14:15,92...

Ma non è finita. Nel capitolo dedicato alla numerologia parleremo della gematria, una tradizione di interpretazione dei testi sacri che associa alle parole dei valori numerici tali da stabilire relazioni nascoste che permetterebbero di scoprire il senso segreto dei testi biblici. I matematici accademici considerano tale disciplina solo una pseudoscienza, ma Robert Gold, un uomo d'affari in pensione, ha applicato un metodo analogo allo studio dei decimali del numero π ed e arrivato alla conclusione che (sono parole sue) « la Bibbia è nel π e il π è nella Bibbia » e « i decimali di π sono il genoma del mondo ». Gold pensa di aver dimostrato che π e la Bibbia sono intimamente legati, trovando numerose coincidenze spiegate nel suo libro « Dio e il numero π » (1997). Il metodo numerologico ideato da Gold è molto più complesso della normale gematria, che si limita ad assegnare valori numerici alle 22 lettere dell'alfabeto ebraico. Il nostro autore associa principalmente quattro numeri a ogni lettera: l'intero tra 1 e 22 che indica la posizione della lettera nell'alfabeto; il "valore semplice" tradizionalmente attribuito dalla gematria, tra 1 e 400; il "valore pieno" che si ottiene scrivendo ogni lettera foneticamente, cosa che da luogo a molte lettere delle quali si sommano i valori semplici; e il "valore finale" ottenuto calcolando in maniera particolare il valore delle ultime lettere delle parole. Robert Gold ha calcolato così i valori di alcune parole importanti della Bibbia scritte in ebraico, tra cui ovviamente « Bibbia », « In principio », « Terra » (ultima parola del primo versetto della Bibbia), « Gerusalemme », eccetera. Per esempio, il valore semplice del nome di Gerusalemme è 596, mentre il suo valore finale è 1156. Ebbene, il numero 31² + 14² (somma dei quadrati delle coppie di cifre che si trovano in 314, le prime tre cifre di π) vale 1157, che è il numero finale di Gerusalemme, a meno di un'unità. Invece 3¹⁴ = 4.782.969; se da questo numero sottraiamo 597, il valore semplice di Gerusalemme aumentato di un'unità, troviamo 4.782.372 che è uguale a 4137 x 1156, il valore finale. Elevando al quadrato 3141, le prime quattro cifre di π, troviamo 9.865.881, e la somma di 588 e 568, numeri estratti da esso a partire dal 5 centrale, è di nuovo 1156. 1413², il quadrato dei primi quattro decimali di π letti al contrario, dà 1.996.569, il che suggerisce, basandosi ancora sul 5, di calcolare 569 + 569 + 19 = 1157, di nuovo 1156 approssimato di una unità. Se invece partiamo dal primi otto decimali di 7, 31415926, li separiamo in tre gruppi (31, 415 e 926) e ne rovesciamo 1'ordine, otteniamo 13 + 514 + 629 = 1156. Non vi basta? Consideriamo addirittura i primi 22 decimali di π: 3141592653589793238462. Li raggruppiamo a due a due tranne il 31, ottenendo 41 + 59 + 26 + 53 + 58 + 97 + 93 + 23 + 84 + 62 = 596. Infine altri calcoli, pur non facendo intervenire la Bibbia, secondo Gold dimostrano che π contiene un messaggio recondito: ad esempio 31 + 41 + 59 + 26 = 157, la metà esatta di 314...

Un'infinità di altre osservazioni di questo tipo ha convinto il nostro numerologo della tesi di un intimo e profondo collegamento tra π e la Bibbia, il che giustificherebbe la sua affermazione secondo cui i decimali 314159... starebbero all'universo come i tre miliardi di basi del nostro genoma stanno all'umanità. A dir la verità, come ha scritto un matematico (uno vero!), saremmo più impressionati se i primi tremila decimali di π raggruppati a tre a tre avessero dato i valori numerici delle prime mille parole nell'ordine del testo della Bibbia, calcolati con la gematria tradizionale, con il metodo di Gold o con una qualunque altra variante numerologica. Ma, purtroppo per il nostro numerologo, non è così; le presunte "scoperte" di Gold dimostrano solo che chi gioca a lungo con i numeri, prima o poi finisce per trovare tutte le dimostrazioni che cerca. Ad esempio, per un matematico "vero" 1156 e 1157 non sono affatto "quasi uguali", sono semplicemente diversi, e nessuna dimostrazione rigorosa può basarsi sulla "somiglianza" tra due numeri: questa non è matematica, è dilettantismo di chi crede di compiere scoperte epocali giocando e rigiocando con il cubo di Rubik. Ne volete una prova? Ebbene, io ho utilizzato questo sito per verificare se tra i primi 100 milioni di cifre decimali di π vi è la mia data di nascita, scritta nella semplice forma 20569 (20 maggio 1969), ed ho scoperto che essa compare a partire dalla 1326esima cifra decimale; ma vi è anche la stringa più lunga 200569 (20/05/69), a partire dalla 418504esina cifra. E compare persino nella forma 20051969 (20/05/1969), a partire dalla 76403313esima cifra. Provate anche voi! Non c'è alcun dubbio che, continuando a cercare, ogni uomo vivente sulla Terra o vissuto nel passato potrebbe rintracciare nel π la propria data di nascita, semplicemente perchè π ha un'infinità di cifre decimali distribuite senza alcun ordine apparente, senza che questo possa trasmetterci alcun messaggio di natura trascendente! Ne riparleremo nell'Appendice a questo ipertesto.

Concludiamo questo capitolo facendo notare che il pi greco è nascosto anche nel Libro dell'Esodo. Infatti se si va a prendere il terzo capitolo di esso e se ne cerca il quattordicesimo versetto, così da ottenere il riferimento 3, 14, ecco cosa si legge: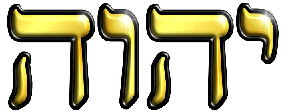

« Dio disse a Mosè: "Io sono colui che sono!" Poi disse: "Dirai agli Israeliti: Io-Sono mi ha mandato a voi". » (Esodo 3, 14)

Non c'è dubbio che questo sia da considerarsi uno dei versetti più importanti dell'intera Bibbia, giacché in esso è rivelato per la prima volta il Sacro Tetragramma YHWH, che vediamo qui a destra. Niente da fare, il π è come il prezzemolo: salta fuori da ogni parte, e quando meno te lo aspetti!