![]()
|
«
Io lo vedo, ma non ora, (Num 24, 17) |
Questa volta ci concentreremo su un episodio che non è tra i più famosi del Pentateuco, ma che ha avuto il merito di ispirare molte suggestioni successive, tra cui quella della stella che tutti noi mettiamo sulla capanna di Gesù Bambino nel nostro presepe. Siamo nel capitolo 22 del Libro dei Numeri, e il protagonista è Balaam, figlio di Beor. Di lui si sa pochissimo, se non che era un profeta pagano e che Balak, re di Moab, mandò a chiamarlo affinché maledisse Israele, percepito come un pericoloso avversario:
« Balak, figlio di Sippor, era in quel tempo re di Moab. Egli mandò messaggeri a Balaam, figlio di Beor, a Petor, che sta sul fiume, nel territorio dei figli di Amau, per chiamarlo e dirgli: "Ecco, un popolo è uscito dall'Egitto; ha ricoperto la faccia della terra e si è stabilito di fronte a me. Ora dunque, vieni e maledici questo popolo per me, poiché esso è più potente di me. Forse riuscirò a batterlo, per scacciarlo dalla terra; perché io lo so: colui che tu benedici è benedetto e colui che tu maledici è maledetto." » (Numeri 22, 4-6)
Petor è una città della Mesopotamia sul fiume Eufrate, ma sembra difficile che il re di un piccolo paese come Moab sia andato così lontano a cercare un mago e profeta, per quanto famoso. Anche il nome "Balaam" non trova spiegazioni in lingua ebraica; la congettura che lo fa derivare da "Belo'Am" ovvero "senza popolo", è una ricostruzione rabbinica molto tarda. Altri lo interpretano come "straniero" o "ghiottone", mentre alcuni esegeti moderni hanno puntato su "Billa'Am", che significa "colui che ha rovinato un popolo", ma anche questa sembra un'etimologia posteriore, dato che egli cercò di distogliere gli Ebrei dal monoteismo. Vi è però un'altra spiegazione. Nel libro della Genesi si elencano i sovrani edomiti (quindi discendenti di Esaù) prima che Saul iniziasse a regnare sugli Ebrei, e si dice:
« Questi sono i re che regnarono nel territorio di Edom, prima che regnasse un re sugli Israeliti. Regnò dunque in Edom Bela, figlio di Beor, e la sua città si chiamava Dinaba. » (Gen 36, 31-32)
Si ipotizza che Bela sia una forma alternativa di Balaam, e quindi questo personaggio sarebbe stato un re Edomita: infatti Dinaba, forse da identificarsi con l'odierna Dibdiba, a nordest di Petra in Giordania, era una delle capitali dell'Idumea.
Ma torniamo al testo biblico. Dopo aver ricevuto l'ambasciata di Balak, Balaam interroga l'Oracolo del Signore, che impone al profeta di rifiutare l'offerta del Re di Moab, nonostante l'insistenza e l'offerta di oro e argento da parte degli ambasciatori: « Dio disse a Balaam: "Tu non andrai con loro, non maledirai quel popolo, perché esso è benedetto." » (Num 22, 12) Durante la notte, però, a sorpresa YHWH cambia idea: « La notte Dio venne da Balaam e gli disse: "Questi uomini non sono venuti a chiamarti? Àlzati dunque, e va' con loro; ma farai ciò che io ti dirò." » (Num 22, 20) Quando il profeta parte, nuovo colpo di scena: « Ma l'ira di Dio si accese perché egli stava andando; l'angelo del Signore si pose sulla strada per ostacolarlo. » (Num 22, 22) Questa serie di contraddizioni viene interpretata dalla moderna esegesi attribuendo il permesso accordato a Balaam da parte del Signore alla Tradizione Elohista, mentre il rifiuto alla Tradizione Jahvista. L'Autore Jahvista insomma non vede di buon occhio i profeti non ebrei, e quindi mette in bocca a Dio l'imposizione a Balaam di stare alla larga da Israele, mentre l'Elohista ammette che Dio possa parlare anche per bocca di profeti pagani, ed infatti Balaam nel racconto Elohista finirà per benedire il Popolo Eletto. Segue un racconto fantastico, in cui l'angelo di Dio sbarra la strada a Balaam, solo la sua asina lo vede, è percossa perchè ha paura di proseguire e si mette a parlare al suo padrone con voce umana. Secondo gli esegeti moderni, anche tale episodio sarebbe di matrice Jahvista: tale autore intenderebbe ridicolizzare il profeta edonita, dal momento che l'angelo lo considera meno della sua cavalcatura: « L'asina mi ha visto e ha deviato davanti a me per tre volte; se non avesse deviato davanti a me, certo ora io avrei già ucciso proprio te e lasciato in vita lei! » (Num 22, 33) Ogni popolo racconta fiabe di animali umanizzati e parlanti: basta pensare alle favole di Esopo e di Fedro, o a quelle di Perrault e di Andersen, ma anche a Huan, il cane parlante di Celegorm nel "Silmarillion" di John Ronald Reuel Tolkien. Nel captolo 23 dei Numeri il genere della fiaba verrebbe utilizzato allo scopo di mostrare la pochezza rispetto all'ebreo Mosè di quello che i Moabiti consideravano il massimo tra i profeti (« colui che tu benedici è benedetto e colui che tu maledici è maledetto » Num 22, 6). La maggior parte dei commentatori ritiene quello dell'asina parlante di Balaam un racconto allegorico, da non prendersi alla lettera, e Rabbi Joseph Herman Hertz (1872-1946), uno dei massimi esegeti ebrei moderni, scrisse che « questi versetti rappresentano la continuazione sul piano subconscio del conflitto mentale e morale nell'anima di Balaam ». Ad ogni modo, ci aspetteremmo che il profeta, terrorizzato dall'apparizione, torni indietro; invece dall'angelo arriva un inaspettato disco verde: « Va' pure con questi uomini; ma dirai soltanto quello che io ti dirò. » (Num 22, 35) Evidentemente, siamo tornati alla Tradizione Elohista, secondo la quale anche il pagano può essere investito dallo Spirito di Dio, anche se in tal caso non parla più per conto proprio, ma è YHWH a parlare per bocca sua.

Gustave Dorè, L'angelo appare a Balaam, incisione, 1866
Alla fine, giunto in vista dell'accampamento degli Ebrei insieme a Re Balak, Balaam non può far altro che obbedire a YHWH e benedire grandemente Israele, benché il sovrano moabita lo avesse pagato per maledirlo: « Dio, che lo ha fatto uscire dall'Egitto, / è per lui come le corna del bufalo. / Perché non vi è sortilegio contro Giacobbe / e non vi è magìa contro Israele: / a suo tempo vien detto a Giacobbe / e a Israele che cosa opera Dio. / Ecco un popolo che si leva come una leonessa / e si erge come un leone; / non si accovaccia, finché non abbia divorato la preda / e bevuto il sangue degli uccisi. » (Num 23, 22-24) Ricordiamo, in proposito, che il leone era il totem della tribù di Giuda. Queste parole provocano la reazione sdegnata di Balak: « Se proprio non lo maledici, almeno non benedirlo! » (Num 23, 25) Niente da fare: Balaam pronuncia ben sette poemi in lode di Israele, prima di tornarsene a casa sua. Alcuni capitoli dopo. Balaam rispunta nelle parole di Mosè come prototipo del nemico di Israele, avendo convinto gli Ebrei a peccare con donne pagane: « Proprio [le donne di Madian], per suggerimento di Balaam, hanno insegnato agli Israeliti l'infedeltà verso il Signore, nella vicenda di Peor, per cui venne il flagello nella comunità del Signore. » (Num 31, 16) Evidentemente anche questo versetto è opera dell'Autore Jahvista. Il profeta comunque fa la fine di tutti gli altri nemici di Israele: « Marciarono dunque contro Madian, come il Signore aveva ordinato a Mosè, e uccisero tutti i maschi. [...] Uccisero di spada anche Balaam figlio di Beor. » (Num 31, 7-8) Si noti che qui, più che ad un Re di Edom, l'Autore Sacro sembra pensare a un profeta dei Madianiti, una tribù araba stanziata intorno al Golfo di Aqaba cui apparteneva Jetro, suocero di Mosè, e che sparì dalla Storia Sacra dopo l'epoca dei Giudici, per ragioni che ci sono ignote.
Di Balaam nella letteratura posteriore si danno solo giudizi negativi, segno che evidentemente ha prevalso il punto di vista Jahvista. Filone di Alessandria (20 a.C. - 45 d.C.) nella sua "Vita di Mosè" descrive Balaam come un mago che « simboleggiava un'accozzaglia di opinioni contrarie e contrastanti », mentre lo storico giudaico Giuseppe Flavio lo considera il miglior profeta del suo tempo dopo Mosè, ma incapace di seguire la dottrina del Vero Dio. Secondo il Talmud Babilonese, Balaam sarebbe stato così potente come indovino e profeta affinché le tribù non israelite non potessero dire: « Saremmo stati pii come gli Ebrei, se solo avessimo avuto anche noi il nostro Mosè ». Nel Nuovo Testamento, i primi cristiani sono messi in guardia dalla Lettera di Giuda e dalla Seconda Lettera di Pietro, che considerano Balaam un falso profeta mosso dalla cupidigia e dall'avarizia:
«
Guai a loro! Perché si sono messi sulla strada di Caino e, per guadagno, si sono lasciati andare alle seduzioni di
Balaam e si sono perduti nella ribellione di Core.
» (Gd 1, 11)
« Abbandonata la retta via, si sono smarriti seguendo la via di Balaam figlio di Bosor, al quale piacevano ingiusti guadagni,
ma per la sua malvagità fu punito: un'asina, sebbene muta, parlando con voce umana si oppose alla follia del profeta.
» (2 Pt 2, 15-16)
Nell'Apocalisse di Giovanni si parla di Balaam nella lettera spedita alla Chiesa di Pergamo, come di colui che traviò gli Israeliti, evidentemente prendendolo a prototipo di personaggi a noi ignoti che cercavano di far ritornare i cristiani di Pergamo al paganesimo:
« Ho da rimproverarti alcune cose: presso di te hai seguaci della dottrina di Balaam, il quale insegnava a Balak a provocare la caduta dei figli d'Israele, spingendoli a mangiare carni immolate agli idoli e ad abbandonarsi alla prostituzione. » (Ap 2, 14)
Nei capitoli 7 e 8 del Vangelo Arabo dell'Infanzia, un apocrifo del Nuovo Testamento scritto tra l'VIII e il IX secolo, i tre Magi che vennero a portare doni a Gesù Bambino sono identificati come sacerdoti della religione zoroastriana, e Zoroastro è identificato proprio con Balaam: entrambi infatti erano considerati contemporanei di Mosè, profeti potwenti secondo i rispettivi popoli e seguaci di un culto monoteistico. Ovviamente l'identificazione è priva di basi storiche. Secondo molti esegeti il falso profeta citato nella settima Sura del Corano, versetti 175-176, che non diede retta ad Allah sarebbe proprio Balaam: « Narra loro, ai Giudei, la storia di colui al quale facemmo vedere un segno e che se ne distolse per seguire Satana e fu tra gli smarriti. Ora, se avessimo voluto, lo avremmo elevato in alto attraverso questo miracolo; ma egli si tenne attaccato alla terra e seguì le sue passioni. »
Dire se Balaam sia realmente esistito o meno, è difficile. È possibile che egli fosse un sacerdote pagano la cui figura è divenuta comune a molte tradizioni semitiche, come Daniele e Giobbe, e così è entrato a far parte anche dell'Antico Testamento: la sua fama universale come profeta giustifica le benedizioni di Israele che gli vengono messe in bocca dagli Autori Biblici. Come Omero, la sua stessa patria d'origine è oggetto di discussioni: Petor in Mesopotamia, Dinaba nel Paese di Edom, la terra di Madian o qualche altra tribù semitica della tarda Età del Bronzo? Alcuni leggono il suo nome "Baal Am", cioè il Baal di Am: in tal caso si tratterebbe di una qualche divinità cananea trasformata in personaggio storico dall'Autore biblico; ed infatti, come un essere semidivino, Balaam vede gli angeli, ha una mula parlante e profetizza il futuro. La spiegazione però non è convincente, perchè alcune importanti figure di Israele portavano nomi contenenti la sillaba "Baal", tra cui il giudice Gedeone, chiamato anche Ierub-Baal ("Baal mi difenda", interpretato però come « Baal difenda la sua causa contro di lui, perché egli ha demolito il suo altare » in Giudici 6, 32), il figlio di re Saul Is-Bosheth, chiamato anche Is-Baal ("uomo di Baal") e il figlio di Gionata Mephi-Bosheth detto Merib-Baal ("Baal è il mio difensore"). Nel 1967 a Deir Alla, oggi in Giordania, gli archeologi hanno riportato alla luce i resti di un edificio, presumibilmente distrutto da un terremoto in epoca persiana, su un muro della quale vi era un'iscrizione che faceva riferimento alle « visioni del veggente Balaam, figlio di Beor », che secondo alcuni potrebbe essere lo stesso citato nel Libro dei Numeri, rafforzando l'ipotesi che egli appartenga ad un sostrato semitico comune a molti popoli dell'area, anche se il Balaam di Deir differisce da quello biblico perchè non è un profeta di YHWH ma di Ashtar-Chemosh, una dea femminile venerata dai Moabiti ed equivalente ad Astarte, la Grande Madre cananea, sposa di Adone e legata alla fertilità, alla fecondità e alla guerra. Questo però non è un problema, perchè anche Daniele, che compare nell'Antico Testamento addirittura come protagonista di un intero libro ed è annoverato tra i Profeti maggiori (gli ho dedicato un apposito ipertesto), appartiene in realtà al corpus sapienziale anche di altre culture semitiche: nei testi di Ugarit, città siriana con una storia lunghissima, Dan'el appare come il prototipo del re giusto e saggio. Nel Poema di Aqhat, capolavoro della letteratura ugaritica composto nel XIV secolo a.C., Dan'el implora il dio El perché non ha figli che gli possano succedere, una situazione molto simile a quella di Abramo; per sette giorni resta nel tempio giorno e notte pregando e piangendo, finché El sollecitato da Baal gli compare in sogno promettendo l'erede, Aqhat. Tra l'altro, il nome del dio El ricorda molto da vicino Elohim, uno degli epiteti di YHWH. La dea Anath però provocherà la morte di Aqhat (ciò ricorda Isacco chiesto in sacrificio da YHWH); allora Dan'el scaglia una maledizione contro gli assassini, e da tutta la terra scompare la vegetazione. Il finale del poema è andato perduto, ma si suppone che Dan'el abbia ottenuto il ritorno sulla terra del figlio nella stagione estiva come nel mito greco di Persefone, dando vita al ciclo delle stagioni. Come si vede, un mito che ha molto in comune con altri a noi noti, ma che non ci aspetteremmo possa avere al centro un personaggio biblico che, per non tradire la sua fede nell'Unico Dio, è finito nella fossa dei leoni!

Le mura megalitiche dell'antica Ugarit (foto tratta da questo sito)
Questo naturalmente non risolve il problema dell'esistenza storica di Balaam. Io penso che alla base sia di Balaam che di Daniele, come di altri personaggi comuni a varie letterature semitiche quali Sansone e Giobbe, vi siano effettivamente delle figure storiche. E lo stesso discorso vale per i protagonisti di altri corpus mitologici, come Gilgamesh, Ercole, Orfeo, Romolo, Quetzalcoatl. Essi però vissero in un'epoca in cui la scrittura non era ancora utilizzata, le loro vicende vennero trasmesse solo oralmente e vennero completamente trasfigurate dal mito, cosicché oggi la loro storicità è per noi irraggiungibile, a meno di clamorose quanto improbabili scoperte archeologiche. E allora? E allora noi ci teniamo i racconti su di loro che sono pervenuti fino a noi, apprezzandoli nella loro bellezza, com'è il caso della mula parlante e del profeta pagano che benedì anziché maledire Israele.
In questa sede ci siamo dilungati a parlare di Balaam per via della profezia contenuta nel quarto dei poemi da lui pronunciati:
« Oracolo di Balaam, figlio di Beor,
oracolo dell'uomo dall'occhio penetrante,
oracolo di chi ode le parole di Dio
e conosce la scienza dell'Altissimo,
di chi vede la visione dell'Onnipotente,
cade e gli è tolto il velo dagli occhi.
Io lo vedo, ma non ora,
io lo contemplo, ma non da vicino:
una stella
spunta da Giacobbe
e uno scettro sorge da Israele,
spacca le tempie di Moab
e il cranio di tutti i figli di Set;
Edom diverrà sua conquista
e diverrà sua conquista Seir, suo nemico,
mentre Israele compirà prodezze.
Uno di Giacobbe dominerà
e farà perire gli scampati dalla città. » (Numeri 24, 15b-19)
La profezia della stella attraverserà tutta la storia d'Israele, fino a giungere al Messia, la cui nascita sarà annunciata proprio dal sorgere di un astro. Del resto Lucifero, la stella del mattino, era la protettrice del re di Babilonia, come ricorda Isaia che identifica l'astro con la città (« Come mai sei caduto dal cielo, astro del mattino, figlio dell'aurora? Come mai sei stato gettato a terra, signore di popoli? » Isaia 14, 12): nelle culture semitiche, la stella è associata alla regalità. La luce accompagna anche il canto messianico di Isaia: « Il popolo che camminava nelle tenebre ha visto una grande luce; su coloro che abitavano in terra tenebrosa una luce rifulse » (Isaia 9, 1). Ed ecco che la nascita di Cristo è rivelata ai Magi (stranieri e profeti come Balaam!) da una stella, come essi stessi spiegano all'allibito Erode nel capitolo 2 del Vangelo di Matteo:
« Nato Gesù a Betlemme di Giudea, al
tempo del re Erode, ecco, alcuni Magi vennero da oriente a Gerusalemme e
dicevano: "Dov'è colui che è nato, il Re dei Giudei? Abbiamo visto spuntare la
sua
stella
e siamo venuti ad adorarlo." » (Mt 2, 1-2)
« Udito il re, essi partirono. Ed ecco, la
stella, che avevano visto spuntare,
li precedeva, finché giunse e si fermò sopra il luogo dove si trovava il
bambino. Al vedere la stella, provarono una gioia grandissima. » (Mt 2, 9-10)
Gli altri evangelisti invece non fanno cenno a fenomeni astronomici contemporanei alla nascita di Gesù, neppure Luca il cui Vangelo dell'Infanzia è il più esteso (alcuni pensano che Luca non volesse parlare bene dei Persiani, popolo da cui i Magi provenivano, essendo all'epoca nemici giurati di Roma). Sulla natura dell'astro che guidò i Magi alla capanna di Betlemme si è acceso un dibattito scientifico che va avanti da duemila anni, arricchendosi continuamente di nuove ipotesi; vale la pena di elencarne qualcuna. Ascoltiamo per primo il parere di Papa Benedetto XVI nel suo bestseller "L'infanzia di Gesù": « Non poteva non essere posta la domanda se non si fosse trattato di un fenomeno celeste determinabile e classificabile astronomicamente. Sarebbe errato rifiutare a priori una simile domanda con il rinviare al carattere teologico del racconto. Con il sorgere dell'astronomia moderna, sviluppata pure da cristiani credenti, è stata posta nuovamente anche la questione circa questo astro. » (cap. 4, pag. 114) Certamente questo astro misterioso nel racconto evangelico appare animato da un moto diverso da quello di tutti gli altri: prima si muove da oriente verso occidente, come una stella normale, ma poi pare spostarsi da nord verso sud, da Gerusalemme verso Betlemme, e alla fine appare immobile sopra la Città di Davide, proprio come fanno i pianeti quando invertono il loro moto apparente rispetto alle stelle fisse.

Balaam indica la stella dei Magi nelle Catacombe di Priscilla
Una delle prime raffigurazioni artistiche dell'episodio di Matteo lo troviamo a Roma, nelle Catacombe di Priscilla, in cui una figura profetica, secondo alcuni proprio il nostro Balaam, indica una stella a dodici punte sopra la Madonna con Bambino. In un mosaico del VI secolo della Basilica di Sant'Apollinare Nuovo a Ravenna, sulla capanna di Gesù Bambino campeggia invece una piccola stella gialla ad otto punte. Colui che associò per primo l'astro di Matteo a una cometa fu, nel III secolo dopo Cristo, Origene di Alessandria (185-284), che nel suo "Contro Celso", scagliandosi contro le superstizioni popolari che indicano le comete come astri portatori di sventura, afferma che, al contrario, esse possono presagire eventi assai positivi, come per l'appunto la nascita di Gesù. Anche altri Dottori della Chiesa, tra cui Giovanni Damasceno (676-749), ribadirono che la stella apparsa ai Magi, considerato il suo corso, non poteva essere che una cometa. Ma a radicare nella tradizione popolare la leggenda della cometa di Natale fu Giotto di Bondone (1267-1337), uno dei più grandi pittori dell'età medioevale, che nell'"Adorazione dei Magi", uno degli stupendi affreschi realizzati nella Cappella degli Scrovegni di Padova all'inizio del Trecento, raffigurò per la prima volta l'astro di cui parla il Vangelo di Matteo come una luminosa cometa. Ciò avvenne perchè nel 1301 l'artista aveva osservato il passaggio della luminosissima cometa di Halley, ed evidentemente si era convinto che fosse questa la stella inviata a guidare i Magi, Da allora, sia nell'iconografia artistica, sia nelle rappresentazioni sacre e popolari, il presepe sarà accompagnato da una vistosa cometa con la coda, al posto della classica stella a tre punte, antico simbolo trinitario. Tuttavia la congettura che la cometa la cui regolarità fu scoperta nel 1705 da Edmund Halley (1656-1742) fosse davvero l'astro dei Magi è priva di fondamento, dato che essa passò accanto alla Terra nel 12 a.C., dunque cinque o sei anni prima della nascita di Cristo.

Giotto, L'Adorazione dei Magi, Cappella degli Scrovegni, Padova


La cometa di Halley ritratta da
Giotto (in alto) a confronto con
una foto della cometa scattata durante l'ultimo passaggio, nel 1986
Ai primi del XVII secolo, l'enigma della stella della Natività fu affrontato dall'astronomo ceco Johannes Kepler (1571-1630), lo scopritore delle leggi sul moto dei pianeti, il quale nella notte del 17 dicembre 1603, con l'ausilio di un rudimentale telescopio, osservò la grande congiunzione dei pianeti Giove e Saturno, cui si aggiunse poco dopo anche Marte. Kepler rimase affascinato da tale fenomeno, e cominciò a chiedersi se la "stella" di Betlemme non potesse essere proprio una congiunzione planetaria. Nell'opera "De anno natali Christi" (1614) il grande astronomo calcolò che effettivamente Giove e Saturno si erano incontrati per ben tre volte nella costellazione dei Pesci nell'anno 7 a.C., il 29 maggio, il 3 ottobre e il 4 dicembre, arrivando alla distanza minima di un grado. L'effetto di questi pianeti stretti insieme nel cielo deve essere stato molto suggestivo, tanto da dare l'impressione di un unico astro luminoso, anche se a Gerusalemme nessuno aveva attribuito loro un significato religioso particolare, né tantomeno uno messianico. La conferma dell'accuratezza dei calcoli di Kepler ci viene da una tavoletta in caratteri cuneiformi rinvenuta a Sippar, antica città babilonese fra il Tigri e l'Eufrate circa 900 chilometri ad est di Gerusalemme, e decifrata nel 1925 dall'erudito tedesco Paul Schnabel (1887-1947), nella quale si parla proprio del triplice avvicinamento dei due astri. Così commenta in proposito lo scrittore Vittorio Messori: « Gli archeologi hanno decifrato la simbologia degli astrologi babilonesi. Ecco i loro risultati: Giove, per quegli antichi indovini, era il pineta dei dominatori del mondo. Saturno il pianeta protettore d'Israele. La costellazione dei Pesci era considerata il segno della "Fine dei Tempi", dell'inizio cioè dell'era messianica. Dunque, potrebbe essere qualcosa di più di un mito il racconto di Matteo dell'arrivo dall'Oriente a Gerusalemme di sapienti, di magi, che chiedono "Dov'è nato il re dei Giudei?" » Ed ecco come Marco Marchetti ricostruisce le osservazioni e l'itinerario dei sapienti venuti dall'Oriente:
« A fine maggio del 7 a.C. i Magi osservano il primo attesissimo avvicinamento dei due pianeti e, recepito il messaggio astrale, partono a dorso di cammello per Gerusalemme. Vi arrivano in corrispondenza del secondo avvicinamento, sono ricevuti da Erode, gli fanno notare il "segno" e apprendono che le antiche profezie davano Betlemme, nove chilometri in direzione sud, come luogo di nascita di Gesù. I Magi si dirigono così a Betlemme durante il secondo avvicinamento; secondo le moderne ricostruzioni in prima serata i due pianeti si trovano in direzione sud-est; la presenza della Luna ne risalta ancora di più la luce poiché indebolisce quella delle stelle; viaggiando verso sud i pianeti si trovano proprio davanti e i Magi hanno come l'impressione di essere preceduti e guidati dalla congiunzione planetaria. Quando i tre arrivano a Betlemme i pianeti sono al meridiano; quando una stella o un pianeta transita al meridiano raggiunge la massima altezza sull'orizzonte (si dice che "culmina") e sembra fermarsi. I Magi vedono così la congiunzione fermarsi sulla casa, entrano e incontrano il Bambino. »
Qui sotto potete osservare una ricostruzione del cielo stellato visto da Gerusalemme verso Sud, cioè verso Betlemme, alle 17.00 ora locale del 4 dicembre del 7 a.C., realizzata con il programma Stellarium: la congiunzione di Giove e Saturno nei pesci è visibilissima!

Sembra una spiegazione molto convincente, tanto da essere fatta propria anche da Werner Keller nel suo classico "La Bibbia aveva ragione". Tuttavia non sono mancate ipotesi alternative. Il cosmologo statunitense Frank Tipler (1947-), noto per i suoi controversi studi sui viaggi nel tempo, ritiene di avere individuato la stella dei Magi in una supernova o una ipernova esplosa nella galassia di Andromeda, che avrebbe culminato allo zenit quando i Magi raggiunsero Betlemme. Tipler asserisce che la supernova in Andromeda spiegherebbe in modo letterale un aspetto misterioso del vangelo di Matteo: il fermarsi della stella proprio sopra Betlemme, perchè il "fermarsi" indicherebbe il raggiungimento dello zenit, istante in cui la stella cessa di fornire una indicazione direzionale. Invece Colin Humphreys (1941-), fisico inglese dell'Università di Cambridge, studiando i fenomeni astronomici citati nelle antiche cronache cinesi della dinastia Han ha trovato nel 1995 la descrizione di una cometa apparsa nel 5 a.C., che era molto luminosa e dotata di una evidente coda: per lui l'evento è perfettamente compatibile con la stella dei Magi. Infine, grande notorietà hanno avuto nel 1999 le tesi dell'astronomo statunitense Michael Molnar relative all'occultamento di Giove da parte della Luna nella costellazione dell'Ariete il 17 aprile del 6 a.C. e le tre congiunzioni, che si verificarono negli anni 3-2 a.C., tra Giove e la stella Regolo della costellazione del Leone, anch'essa un simbolo regale. E chi più ne ha, più ne metta!
Naturalmente, a fronte di tanti studi e ricerche che hanno scovato soluzioni veramente ingegnose per l'enigma di Matteo 2, bisogna anche registrare l'opinione di tanti teologi, i quali si domandano perché accanirsi con gli strumenti della scienza per tentare di spiegare un fenomeno che, secondo loro, è rappresentato da un'apparizione esclusivamente preternaturale, una luce miracolosa apparsa per volere divino nell'universo degli uomini in concomitanza della Natività: un annuncio soprannaturale di una nascita soprannaturale. Tra questi vi sono Sant'Ignazio di Antiochia (35-107) e il grande Giovanni Crisostomo (349-407), secondo Patriarca di Costantinopoli, il quale scrisse: « Che questa non fosse una stella comune, anzi, secondo me, che non fosse affatto una stella, ma un potere invisibile che aveva assunto tale sembianza, mi sembra derivare anzitutto dalla via che essa aveva presa. Non esiste, infatti, neppure una sola stella che si muova in quella direzione. » (Omelie sul Vangelo di Matteo VI, 2). In ogni caso, che sia trattato di un'apparizione preternaturale o di un reale fenomeno astronomico, fin dall'inizio della predicazione apostolica Gesù Cristo è associato all'immagine della stella, tanto che San Giovanni nell'epilogo della sua Apocalisse scrive:
« Io, Gesù, ho mandato il mio angelo per testimoniare a voi queste cose riguardo alle Chiese. Io sono la radice e la stirpe di Davide, la stella radiosa del mattino. » (Ap 22, 16)
Il fatto che la nascita del Messia, dopo la profezia di Balaam, sia associata all'apparizione di una stella è testimoniato anche dalla vicenda di Simone Bar Kokhba (in ebraico שמעון בר כוכבא), un rivoluzionario che nel 132 dopo Cristo si proclamò Messia e si pose a capo dell'ultima ribellione giudaica contro l'Impero Romano. Rabbi Akiva ben Joseph, detto Rosh la-Chakhamim ("Capo di tutti i Saggi"), una delle maggiori figure dell'ebraismo di ogni tempo, lo riconobbe ufficialmente come Messia; secondo lo stesso Simone, la sua nascita sarebbe stata annunciata proprio dalla comparsa di una stella, da cui il suo epiteto di Bar Kokhba, "il figlio della stella". Simone si autonominò Nasi ("Principe") e batté moneta, ma l'imperatore Adriano gli invio contro il generale Giulio Severo, che nel 135 d.C. lo sconfisse ed uccise nella Battaglia di Betar. Gli stessi che avevano acclamato Simone come il Messia lo ribattezzarono Bar Koshba, "il figlio della menzogna"; gli Ebrei furono definitivamente cacciati dalla Terra dei Padri, Gerusalemme venne ricostruita come città pagana con il nome di Elia Capitolina, ed iniziò l'era della diaspora. Anche questo episodio è legato alla profezia di Numeri 24, come quello dell'astro dei Magi, anche se nei nostri anni duemila, quando onoriamo la tradizione collocando una scintillante stella dorata sulla capanna del presepe o sulla punta dell'abete natalizio, non ci sfiora nemmeno l'idea che essa possa derivare dalla profezia di Balaam, pronunciata trentatrè secoli fa nelle steppe di Moab!
Ci siamo dilungati tanto a lungo sulle stelle nella Bbbia perchè esse ci danno l'occasione di compiere un excursus nell'astronomia. Questa scienza, nata all'epoca dei Sumeri per trarre vaticini sul presente e sul futuro (un'eredità di questa antica funzione sopravvive nella moderna astrologia), si trasformò in una branca della Matematica non appena si trattò di stabilire con grande precisione la posizione degli astri nello spazio: nacque cos la cosiddetta "astronomia posizionale". Al centro di questa scienza vi è la sfera celeste, definita come una sfera ideale con centro nel punto di osservazione e raggio arbitrario, sulla quale si proiettano tutti i corpi celesti. Tali corpi vanno quindi ad occupare delle posizioni sulla superficie della sfera; è evidente che, per individuare univocamente queste posizioni, ci dovremo avvalere di una geometria valida non su un piano, come la comune geometria euclidea, ma sulla superficie di una sfera. Fu così che nacque la trigonometria sferica, il ramo della geometria che si occupa delle relazioni tra lati ed angoli dei poligoni ed in particolare dei triangoli costruiti su di una superficie sferica; oggi è di notevole importanza non solo per i calcoli astronomici, ma anche per la navigazione sia aerea che marittima. Il primo trattato conosciuto di trigonometria sferica è il "Libro degli archi sconosciuti di una sfera", scritto nel 1060 d.C. dal matematico arabo Abū ʿAbd Allāh Muḥammad ibn Muʿādh al-Jayyānī (989-1079), nativo di Cordova. Grandi contributi alla nascita di questa scienza diedero anche l'altro arabo spagnolo Jābir ibn Aflaḥ al-Ishbīlī (1100-1150) e l'erudito tedesco Johannes Müller, detto Regiomontano (1436-1476).
Partiamo dai concetti basilari. Intersecando una superficie sferica con un piano passante per il suo centro si ottiene una circonferenza detta geodetica; le geodetiche rappresentano le circonferenze di raggio massimo ottenibili sulla superficie sferica, il cui raggio è pari a quello della sfera. Ad esempio, ipotizzando che la Terra sia una sfera perfetta, i meridiani sono tutti geodetiche, ma tra i paralleli l'unica geodetica è l'equatore. Due geodetiche diverse si intersecano in due punti diametralmente opposti; ad esempio, due meridiani terrestri si intersecano nei poli Nord e Sud. L'insieme di tutte le geodetiche che si intersecano negli stessi punti P e Q è detto fascio di geodetiche di poli P e Q; per esempio, l'insieme di tutti i meridiani terrestri rappresenta un fascio di geodetiche i cui poli coincidono con i poli Nord e Sud. Se invece intersechiamo la superficie sferica con un piano che non passa per il centro, l'intersezione è una circonferenza che ha raggio minore del raggio della sfera, e si dice circonferenza minore; il centro di questa circonferenza minore è il piede della retta perpendicolare condotta dal centro O della sfera al piano secante. Per esempio, tutti i paralleli terrestri diversi dall'equatore sono circonferenze minori. Si dice inoltre antipodo di un punto della sfera il simmetrico di tale punto rispetto al centro della sfera.
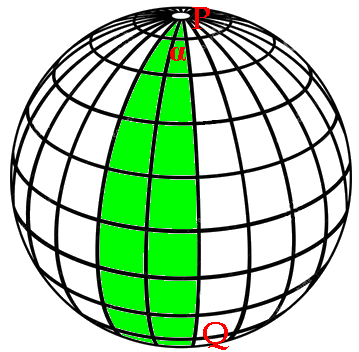
Se due cerchi massimi si incontrano nel punto A, le tangenti ai detti cerchi massimi formano un angolo detto angolo sferico. Due circonferenze massime dividono la superficie sferica in quattro regioni dette fusi sferici. Ogni fuso (in verde nella figura soprastante) è delimitato da due semicirconferenze massime dette lati del fuso, ed i loro estremi si dicono vertici del fuso; i piani in cui giacciono tali semicirconferenze massime danno vita a quattro angoli diedri. Il piano passante per il centro della sfera e perpendicolare al diametro avente per estremi i vertici del fuso taglia il fuso stesso secondo un arco detto sezione normale di quel fuso. I punti P e Q sono i vertici di due angoli sferici entrambi di misura α; indicheremo tale fuso con la scrittura Φ(α). Un fuso si dice retto, acuto o ottuso a seconda che la sua sezione normale sia uguale, minore o maggiore di un quadrante. L'area S(α) di un fuso di angolo α sta alla superficie della sfera come l'angolo α sta a 2π:
S(α) : 4 π R2 = α : 2π
da cui si ricava:
S(α) = 2 α R2
Una spezzata sferica chiusa formata da archi di circonferenze massime divide la superficie sferica in due parti, ciascuna delle quali si chiama poligono sferico; poligono sferico convesso è quello che non contiene il prolungamento dei lati, poligono sferico concavo quello che li contiene. I poligoni sferici, come i poligoni della geometria piana, prendono il nome dal numero dei lati che lo compongono. In particolare, se il poligono sferico è formato da tre lati, si parla di triangolo sferico. È importante ricordare che ogni triangolo sferico è formato da tre archi di cerchio massimo, non da tre archi di cerchio minore qualsiasi.
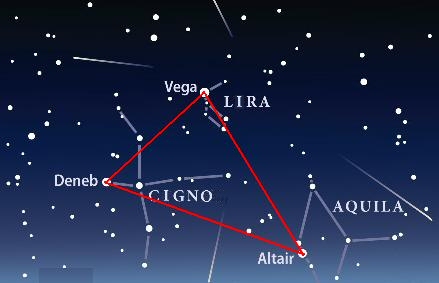
In astronomia posizionale il triangolo sferico prende il nome di triangolo astronomico: dati tre punti sulla sfera celeste (ad esempio tre stelle), questo triangolo si costruisce unendo questi tre punti con degli archi al cerchio massimo. Un classico esempio è rappresentato dal cosiddetto "triangolo estivo", i cui vertici coincidono con le stelle Altair nella costellazione dell'Aquila, Deneb nella costellazione del Cigno e Vega nella costellazione della Lira (quest'ultima è la quinta stella più luminosa del cielo). Nell'emisfero boreale queste tre stelle appaiono appena dopo il tramonto da giugno ai primi giorni di gennaio. Sullo sfondo della Via Lattea, questo triangolo è facilmente identificabile e serve come punto di partenza per individuare le costellazioni vicine:
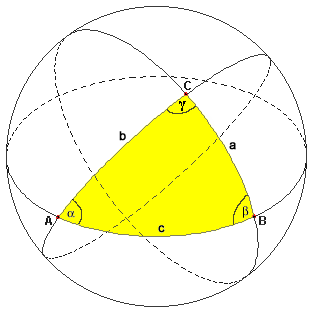
Gli archi di circonferenza massima a, b, c si dicono lati del triangolo sferico, mentre α, β e γ si dicono angoli del triangolo. Più precisamente si indicano con a, b e c le misure dei lati opposti rispettivamente ai vertici A, B e C, e con α, β e γ le misure degli angoli aventi vertici rispettivamente in A, B e C. Ad ogni triangolo sferico ABC corrisponde un triedro avente per vertice il centro O della sfera e per spigoli le semirette passanti per i vertici del triangolo. Essendo gli angoli del triangolo sferico sezioni rette dei diedri corrispondenti, ed essendo i lati del triangolo sferico archi di circoli massimi aventi come angoli al centro le facce del diedro, è evidente che le misure degli angoli e dei lati del triangolo sferico sono rispettivamente le misure dei diedri e delle facce del triedro corrispondente. Nello studio dei triangoli sferici, i lati si misurano in gradi come gli angoli, e questo li distingue nettamente dai triangoli piani. Come conseguenza, due triangoli sferici possono avere gli stessi lati e gli stessi angoli, ma essere di dimensioni diverse, perchè tracciati su superfici sferiche di diverso raggio; invece due triangoli piani con i lati congruenti sono necessariamente congruenti. Ma l'effettiva dimensione dei triangoli sferici non ha alcun significato in trigonometria sferica, interessandoci solo le loro dimensione angolare, così come agli astronomi non interessa il raggio della sfera celeste, ma solo le posizioni su di essa occupate dagli astri.
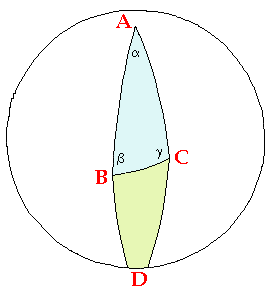
Consideriamo ora il triangolo sferico ABC rappresentato in azzurro nella figura qui sopra: noi possiamo pensarlo come l'intersezione dei fusi sferici Φ(β) di angolo β e Φ(γ) di angolo γ. Ma l'area dell'unione di tali fusi è data dalla somma delle loro singole aree diminuita dell'area del triangolo ABC che, altrimenti, verrebbe contato due volte:
S( Φ(β) U Φ(γ) ) = 2 β R2 + 2 γ R2 – S(ABC)
Se all'unione dei due fusi Φ(β) e Φ(γ) si aggiunge il triangolo individuato dagli antipodi di B, C e D, congruente con il triangolo BCD, si copre un'intera semisfera. Dunque sommando all'area dell'unione di Φ(β) e Φ(γ) l'area del triangolo BCD, si ottiene l'area di mezza sfera:
S( Φ(β) U Φ(γ) ) + S(BCD) = 2 π R2
Sostituendo la prima espressione nella seconda si ottiene:
2 β R2 + 2 γ R2 – S(ABC) + 2 α R2 – S(ABC) = 2 π R2
Da qui è immediato ricavare l'area del triangolo sferico ABC:
S(ABC) = ( α + β + γ – π ) R2
Dato che l'area di un triangolo sferico deve essere positiva, se ne deduce che:
α + β + γ > π
In altre parole, la somma degli angoli interni di un triangolo sferico è maggiore di un angolo piatto. Si tratta di un risultato sbalorditivo, perchè anche gli alunni delle scuole medie sanno che la somma degli angoli interni di un triangolo piano è pari a 180°, cioè a π radianti! Eppure, questo risultato è evidente nel fascio dei meridiani terrestri: due meridiani tra loro perpendicolari formano entrambi angoli retti con l'equatore e, convergendo in un polo, formano un angolo retto tra di loro, quindi la somma dei loro angoli interni è pari a 270°! Un triangolo sferico come questo prende il nome di triangolo trirettangolo.

L'angolo di cui la somma degli angoli sferici interni del triangolo sferico supera l'angolo piatto si chiama eccesso sferico, e lo si indica con ε: ε = α + β + γ – π. Come si è visto sopra, l'eccesso sferico è anche il rapporto tra l'area del triangolo sferico e il quadrato del raggio della sfera cui essa appartiene: ε = S/R2. Consideriamo dunque dei triangoli sferici con la stessa area, ma tracciati su sfere di raggio diverso; l'eccesso sferico allora è inversamente proporzionale al quadrato del raggio. L'eccesso sferico è nullo solo quando il raggio è infinito; in questa circostanza si parlerà di piano al posto di superficie sferica, e di rette al posto di circoli massimi: si torna così alla geometria piana. Nel triangolo sferico trirettangolo della figura precedente, l'eccesso sferico è pari a 270° – 180° = 90°. La sua area è allora uguale a π R2/2, che in effetti è pari a un ottavo della superficie sferica: il triangolo rettangolo equivale infatti a un ottante di cerchio.
Passiamo ora ad un particolare triangolo sferico, il triangolo sferico rettangolo. Supponiamo che l'angolo interno AĈB sia retto; è facile ricavare che in un triangolo sferico rettangolo la differenza degli angoli acuti è minore di 90°, e ogni cateto è della stessa specie dell’angolo opposto, cioè se l'uno è acuto, è acuto anche l'altro, e se l'uno è ottuso, è ottuso anche l'altro. Inoltre il cateto ottuso è maggiore dell’angolo opposto, ed il cateto acuto è minore dell’angolo opposto. L'ipotenusa poi è acuta se i cateti sono acuti oppure ottusi, è retta se i cateti sono l’uno retto e l’altro no, è ottusa se i cateti sono l’uno acuto e l’altro ottuso.
Fissiamo dunque un sistema di riferimento cartesiano ortogonale con origine nel centro O, tale che il piano Oyz coincida con il piano in cui giace il lato AC (in verde nella figura), e il piano Oxz coincida con il piano in cui giace il lato BC (in giallo nella figura):
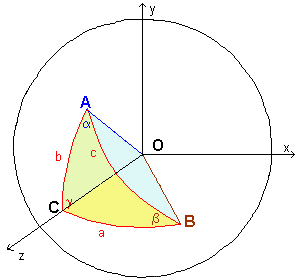
I segmenti OA e OB possono essere descritti come vettori di modulo R (rappresenteremo i vettori sottosegnandoli per semplicità). Ricordiamo che i lati di un triangolo sferico si misurano con i rispettivi angoli al centro della sfera; indicando dunque con a la misura dell'angolo AÔC, con b la misura dell'angolo BÔC e con i, j e k i versori degli assi cartesiani, si ha:
OA = R (sen a j + cos a k)
OB = R (sen b i + cos b k)
Il prodotto scalare dei due vettori può essere calcolato sommando i prodotti delle componenti omonime (cioè il prodotto delle due componenti lungo x più il prodotto delle due componenti lungo y più il prodotto delle due componenti lungo z. Come si vede, il vettore OA ha componente lungo x nulla e il vettore OB ha componente lungo y nulla, per cui non resta che da eseguire il prodotto delle componenti lungo z:
OA x OB = R2 cos a cos b
Ma il prodotto scalare dei due vettori può essere ottenuto anche moltiplicando i loro moduli per il coseno dell'angolo tra di essi compreso. L'angolo compreso tra OA e OB è l'angolo AÔB e misura c, per cui:
OA x OB = R2 cos c
Dal confronto delle due precedenti espressioni si ottiene quindi:
cos a cos b = cos c
Se ne deduce il teorema fondamentale dei triangoli rettangoli sferici o regola dei coseni: il coseno dell'ipotenusa è uguale al prodotto dei coseni dei due cateti.
Consideriamo ora sulla faccia COB la perpendicolare B'C' allo spigolo OC, condotta da un punto B' preso a piacere sullo spigolo OB; successivamente conduciamo sulla faccia COA la perpendicolare C'A' allo spigolo OA; uniti, infine, A' con B', otteniamo i quattro triangoli OA'C' rettangolo in A' per costruzione, OC'B' rettangolo in C' per costruzione, A'B'C' rettangolo in C' per ipotesi e OA'B' rettangolo in A' per il teorema delle tre perpendicolari (se dal piede di una perpendicolare ad un piano si conduce la perpendicolare ad un'altra retta del piano, quest'ultima risulta perpendicolare al piano delle prime due):
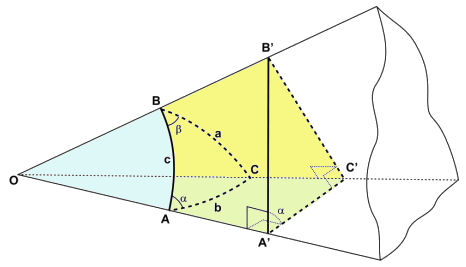
Prendendo in considerazione il triangolo A'B'C', che è piano, abbiamo per note proprietà della trigonometria piana:
B'C' = A'B' sen α , A'C' = A'B' cos α , B'C' = A'B' tg α
Consideriamo ora, per ognuna di esse, i due triangoli rettangoli aventi in comune la semiretta passante per il centro O della sfera ed il vertice comune. Per esempio nella prima il vertice comune è B'. e quindi i due triangoli da considerare sono OA'B' e OC'B'. Siccome A'B' = OB' sen c e B'C' = OB' sen a, la prima delle tre precedenti diventa:
OB' sen a = OB' sen c sen α
da cui si ricava:
sen a = sen c sen α
Ed ecco il secondo teorema fondamentale dei triangoli rettangoli sferici o regola dei seni: il seno di un cateto è uguale al prodotto del seno dell’ipotenusa per il seno dell’angolo opposto. Analogamente le altre forniscono:
tg b = tg c cos α
tg a = sen b tg α
Cioè la tangente di un cateto è uguale al prodotto della tangente dell'ipotenusa per il coseno dell'angolo compreso, oppure al prodotto della tangente dell'angolo ad esso opposto per il seno dell’altro cateto (regola delle tangenti). Dal triangolo OA'B' ricaviamo poi:
![]()
da cui:
cos c = cos a cos b
Dunque il coseno dell'ipotenusa è pari al prodotto dei coseni dei due cateti. Usando queste proprietà appena dimostrate, è facile ottenere poi:
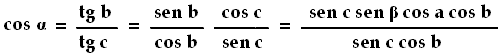
Di conseguenza:
cos α = sen β cos a
Quindi il coseno di un angolo non retto è uguale al prodotto del coseno del lato opposto per il seno dell’altro angolo non retto. In modo analogo si dimostra che:
cos β = sen α cos b
Moltiplicando membro a membro le ultime due, si ha:
cos α cos β = sen α sen β cos a cos b
che si può riscrivere:
cos a cos b = cotg α cotg β
e quindi, per il teorema fondamentale dei triangoli rettangoli sferici:
cos c = cotg α cotg β
Se ne conclude che il coseno dell'ipotenusa è pari al prodotto delle cotangenti degli angoli adiacenti (regola delle cotangenti). I teoremi ora enunciati permettono di risolvere i triangoli rettangoli sferici, così come i teoremi della trigonometria piana permettono di risolvere i triangoli rettangoli piani.
Facciamo un esempio numerico. Di un triangolo sferico ABC, rettangolo in B, sono noti a = 51° 32' 15' e c = 54° 26' 40'. Bisogna trovare gli elementi incogniti, cioè gli angoli α e γ e il cateto c. Trasformando gli angoli in frazioni di grado ed usando la regola dei coseni, con una comune calcolatrice scientifica si ha:
cos b = cos a cos c = cos 51°,5375 x cos 54°,4444 = 0,6220 x 0,5815 = 0,3617
da cui b = 68°,7960 = 68° 47' 46''. Dalla regola dei seni sen a = sen b sen α si ricava allora:
sen α = sen a / sen b = sen 51°,5375 / sen 68°,7960 = 0,7830 / 0,9323 = 0,8399
da cui α = 57°,1271 = 57° 7' 37''. Analogamente la regola dei seni sen c = sen b sen γ permette di ricavare:
sen γ = sen c / sen b = sen 54°,4444 / sen 68°,7960 = 0,8136 / 0,9323 = 0,8726
da cui γ = 60°,7657 = 60° 45' 57''. Si osservi che l'eccesso sferico di questo triangolo vale 90° + 57° 7' 37'' + 60° 45' 57'' – 180° = 27' 53' 34''. E siccome tale angolo equivale a 0,4868 radianti, se ne deduce che l'area di questo triangolo è pari al 48,7 % del quadrato del raggio della sfera su cui esso è disegnato, ovvero al 3,9 % dell'area dell'intera superficie sferica!
Questi metodi per risolvere i triangoli sferici, applicabili alla misura dei triangoli astronomici, non possono non farci tornare in mente le parole del Secondo Isaia, riferite all'onnipotenza di YHWH:
«
Chi ha misurato con il cavo della mano le acque del mare
e ha calcolato l'estensione dei cieli con il palmo?
Chi ha valutato con il moggio la polvere della terra
e ha pesato con la stadera le montagne
e i colli con la bilancia? » (Isaia 40, 12)
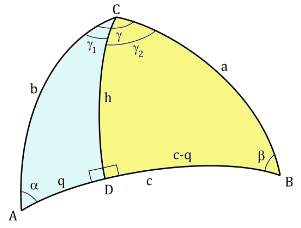
Passiamo ora ad un triangolo sferico qualunque ABC di lati a, b, c e di angoli α, β e γ, come quelo qui sopra. Dal vertice C tracciamo l'arco di cerchio massimo CD perpendicolare al lato AB, che chiameremo altezza del triangolo relativa al lato AB. L'angolo γ è diviso da CD nei due angoli γ1 e γ2, mentre il lato AB è diviso negli archi q e c − q. Applichiamo ai due triangoli rettangoli ADC (in azzurro) e BDC (in giallo) la regola dimostrata sopra secondo cui il seno di un cateto è uguale al prodotto del seno dell’ipotenusa per il seno dell’angolo opposto, ed otteniamo rispettivamente:
sen h = sen b sen α
sen h = sen a sen β
Per la proprietà transitiva dell’uguaglianza, se ne ricava:
sen b sen α = sen a sen β
e in modo analogo si dimostra che:
sen b sen γ = sen c sen β
Il che ci permette di scrivere:
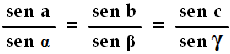
Questo è noto come Teorema dei Seni: i seni dei lati sono proporzionali ai seni degli angoli opposti.
Si consideri ora il triangolo rettangolo sferico BCD (in giallo). In esso si ha:
cos a = cos h cos ( c – q )
Nel triangolo rettangolo sferico ADC (in azzurro) invece
cos b = cos q cos h
Ricaviamo cos h e sostituiamola nella precedente:
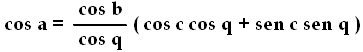
Da cui:
cos a = cos b cos c + sen c cos b tg q
Ora, dal triangolo sferico rettangolo ADC (in azzurro) otteniamo:
cos α = cotg b tg q
che si può riscrivere:
tg q = cos α tg b
Sostituendo nella precedente si trova:
cos a = cos b cos c + sen c cos b tg b cos α
da cui, in definitiva:
cos a = cos b cos c + sen c sen b cos α
Tramite permutazione circolare si ricavano le analoghe relazioni tra lati ed angoli di un triangolo sferico:
cos b = cos c cos a + sen a sen c cos β
cos c = cos a cos b + sen b sen a cos γ
Questo prende il nome di Teorema del Coseno (o Teorema di Eulero), e fornisce la relazione tra tre lati ed un angolo.
In modo analogo, è possibile ricavare il Teorema delle Cotangenti:
cotg a sen c = cos c cos γ + sen β cotg α
da cui, mediante permutazione circolare:
cotg b sen a = cos a cos α + sen γ cotg β
cotg c sen b = cos b cos β + sen α cotg γ
cotg a sen b = cos b cos γ + sen γ cotg α
cotg b sen c = cos c cos α + sen α cotg β
cotg c sen a = cos a cos β + sen β cotg γ
Esso fornisce la relazione tra due lati e tre angoli.
Vediamo ora di risolvere un esempio pratico. Di un triangolo sferico ABC sono noti a = 43° 08' 30', c = 65° 04' 45' e β = 91° 52' 30''; determiniamo gli elementi incogniti, cioè il lato b e gli angoli α e γ. Come si vede, si tratta di un problema assolutamente analogo a quelli della trigonometria piana, in cui bisogna risolvere un triangolo qualunque noti due lati e l'angolo compreso fra di essi, con l'unica differenza che abbiamo a che fare solo con angoli, non con misure lineari.
Tanto per cominciare, determineremo b usando il Teorema del Coseno, dopo aver trasformato gli angoli in frazioni di grado:
cos b = cos c cos a + sen a sen c cos β = cos 65°,0792 x cos 43°,1417 + sen 43°,1417 x sen 65°,0792 x cos 91°,8667 = 0,4214 x 0,7297 + 0,6838 x 0,9069 x ( – 0,0326) = 0,3075 – 0,0202 = 0,2873
Da cui, usando una comune calcolatrice tascabile, si ricava b = 73°,3046 = 73° 18' 16''.
Ora calcoliamo γ usando il Teorema delle Cotangenti. Dalla sesta delle relazioni sopra scritte si ricava infatti:
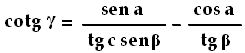
Con facili calcoli si trova cotg γ = 0,3417, e quindi γ = 71°,3044 = 71° 8' 12''. Resta da determinare solo α, che troveremo usando la formula inversa della prima espressione del Teorema delle Cotangenti:
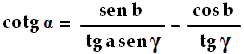
Da qui abbiamo cotg α = 0,9818, da cui α = 45°,5261 = 45° 31' 34''. Allo stesso risultato si poteva giungere anche utilizzando il Teorema dei Seni: sen a : sen α = sen b : sen β. In tal caso si trova sen α = sen a x sen β / sen b = 0,7135, da cui nuovamente α = 45° 31' 34''.
Com'è noto, la trigonometria piana viene utilizzata per risolvere numerosi problemi di topografia, come ad esempio determinare la distanza di due punti entrambi inaccessibili. Anche la trigonometria sferica può avere svariate applicazioni topografiche; vogliamo esaminare dunque almeno una di esse. Sfrutteremo quanto abbiamo imparato per risolvere il problema seguente: determinare la distanza di due punti sulla superficie sferica.
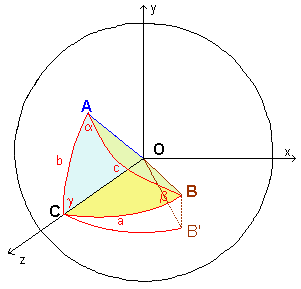
Allo scopo, siano A e B due punti su una superficie sferica di raggio R. Indicando con C il punto dell'equatore sullo stesso meridiano di A, come si vede nella figura soprastante, i vettori OA e OB in coordinate cartesiane possono essere così espressi:
OA = R ( sen b j + cos b k )
OB = R ( cos BÔB' sen B'ÔC i + sen BÔB' j + cos BÔB' cos B'ÔC k )
Il prodotto scalare dei due vettori è pari a:
OA x OB = R2 ( sen b sen BÔB' + cos b cos BÔB' cos B'ÔC )
Ma tale prodotto scalare è esprimibile anche così:
OA x OB = R2 cos AÔB
E quindi:
cos AÔB = sen b sen BÔB' + cos b cos BÔB' cos B'ÔC
Ma l'arco AB si può ottenere moltiplicando il raggio R per l'angolo al centro AÔB espresso in radianti. Ne consegue che la distanza AB sulla superficie sferica si può determinare mediante la formula:
AB = arc cos ( sen b sen BÔB' + cos b cos BÔB' cos B'ÔC )
Osserviamo che, assumendo la Terra sferica, se A e B sono due punti della superficie terrestre e C si trova sull'equatore, l'angolo b rappresenta la latitudine del punto A, l'angolo BÔB' è la latitudine del punto B e l'angolo B'ÔC è la differenza tra la longitudine di A e quella di B, grandezze che noi indicheremo così: b = lat(A), BÔB' = lat (B) e B'ÔC = long(B) – long(A). Da qui ricaviamo la formula per trovare la distanza di due punti sulla superficie terrestre:
AB = arc cos ( sen lat(A) sen lat (B) + cos lat(A) cos lat (B) cos (long(B) – long(A)) )
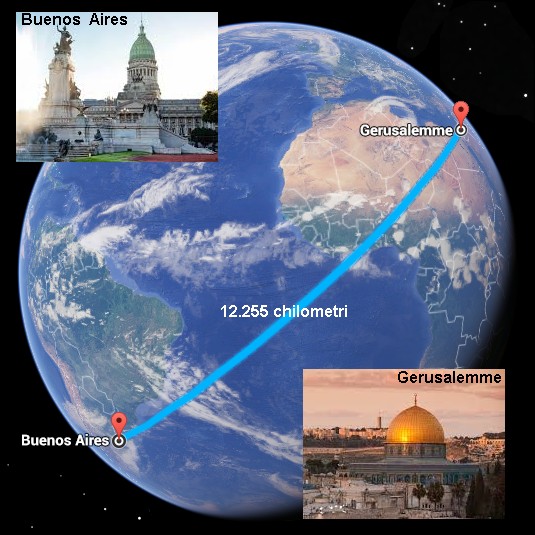
Proviamo a determinare, mediante questa formula, la distanza tra Gerusalemme e Buenos Aires (la città natale di Papa Francesco). Le coordinate geografiche di Gerusalemme sono 31° 46' 8'' Nord e 35° 12' 58'' Est; quelle di Buenos Aires sono 34° 36' 30'' Sud e 58° 22' 19'' Ovest. Trasformando questi angoli in frazioni decimali di grado, e chiamando A la posizione di Buenos Aires e B quella di Gerusalemme, si ha lat (A) = 31°,7689, lat (B) = – 34°,6083 e long (B) – long(A) = 35° 12' 58'' – ( – 58° 22' 19'' ) = 93°,5881. Sostituendo nella formula precedente si ottiene:
cos AB = [sen ( 31°,7689 ) x sen ( – 34°,6083 ) + cos ( 31°,7689 ) x cos ( – 34°,6083 ) x cos ( 93°,5881)] = – 0,3428
Da cui si ricava che l'angolo al centro che insiste sull'arco AB misura 1,9207 radianti. Moltiplicando tale misura per quella del raggio medio del pianeta Terra (il raggio di una ipotetica sfera perfetta con la stessa superficie della Terra), pari a 6371 km, si ottiene la distanza cercata fra le due città, che risulta pari a 12.236 km. In realtà però la Terra non è una sfera ma un geoide, una superficie perpendicolare in ogni punto alla direzione della verticale, cioè alla direzione della forza di gravità, che corrisponde pressappoco ad un ellissoide schiacciato ai poli; misure più accurate ci dicono che in realtà la distanza in linea d'aria fra Gerusalemme e Buenos Aires è di 12.255 chilometri. L'errore da noi commesso nel nostro calcolo è però solo dello 0,15 %, e ciò conferma la bontà di quanto abbiamo esposto in questa lezione circa i metodi della trigonometria sferica!
Fra l'altro, la distanza tra la Città Santa per i tre Monoteismi e la patria di Papa Francesco non può non ricordarci questo celeberrimo passaggio del Salmista:
«
Quanto dista l'oriente dall'occidente,
così egli allontana da noi le nostre colpe. » (Sal 103, 12)
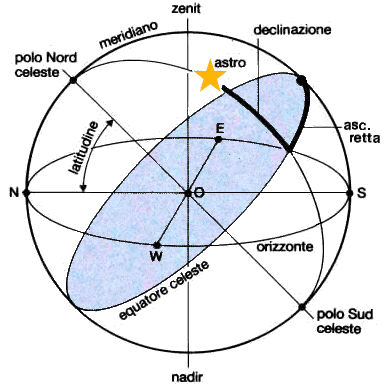
Ovviamente le regole da noi fornite sopra per la risoluzione di un triangolo sferico qualunque sono fondamentali in astronomia per descrivere il triangolo astronomico di cui si è parlato sopra. Senza volerci dilungare eccessivamente su questo complesso argomento, accenniamo qualcosa a proposito delle coordinate celesti. Si dice verticale la direzione data dal filo a piombo applicato al punto O in cui si trova l'osservatore nel momento in cui osserva la sfera celeste. Essa interseca la sfera celeste in due punti: si chiama zenit (dall'arabo samt al-ra's, "direzione della testa") il punto che si trova sopra la testa dell'osservatore, e nadir (dall'arabo nazìr al-samt, "in direzione opposta") il punto diametralmente opposto ad esso. Prendiamo un piano passante per O e perpendicolare alla verticale; l'intersezione di questo piano con la sfera celeste è una circonferenza chiamata orizzonte celeste. Tutti i piani paralleli all'orizzonte celeste che intersecano la sfera celeste formano dei cerchi che prendono il nome di cerchi di altezza. Si definisce piano meridiano il piano individuato dalla verticale e dalla linea dei poli, passante per l'osservatore e parallela all'asse di rotazione terrestre; esso interseca la sfera celeste formando un cerchio, perpendicolare all'orizzonte celeste, chiamato meridiano celeste. Il meridiano celeste interseca l'orizzonte celeste in due punti: il Nord e il Sud. L'Est e l'Ovest, invece, si definiscono dall'intersezione della perpendicolare, passante per O, al segmento che unisce il Nord e il Sud.
Fissato tutto questo, si dice ascensione retta α di un punto sulla volta celeste la distanza angolare fra il meridiano fondamentale e il meridiano passante per il punto scelto, misurata lungo il parallelo passante per l'oggetto celeste. L'ascensione retta è dunque analoga alla longitudine, ma proiettata sulla sfera celeste anziché sulla superficie terrestre. Ascensione retta pari a zero corrisponde al Punto d'Ariete, cioè al punto dell'equinozio primaverile. L'ascensione retta è misurata in ore, minuti e secondi, corrispondenti alla rotazione terrestre: 24 ore di ascensione retta sono un giro completo, e un'ora equivale a 15 gradi. Invece la declinazione δ è l'angolo celeste al centro della terra sotteso da un arco di meridiano celeste compreso fra l'equatore celeste e il parallelo passante per il punto considerato: insomma, è la latitudine proiettata sulla sfera celeste anziché sulla superficie terrestre. La si misura in gradi, e per convenzione i punti a nord dell'equatore celeste hanno declinazione positiva, mentre quelli al di sotto hanno declinazione negativa. L'equatore celeste ha una declinazione di 0°, il Polo Nord celeste ha una declinazione di +90° e il Polo Sud celeste ha una declinazione di − 90°. Le coordinate definite da questo sistema sono quelle riportate nei cataloghi stellari, in quanto indipendenti dal luogo e dall'ora di osservazione; ad esempio, la stella Vega ha ascensione retta di 18h 36min 56,3364s e declinazione +38° 47′ 1,291″. In realtà anche questo sistema dipende dal tempo, a causa del moto proprio delle stelle e dello spostamento lento ma graduale del Punto d'Ariete per effetto del moto di precessione dell'asse terrestre; per questo è necessario specificare l'epoca astronomica a cui ci si riferisce. L'ascensione retta α può essere usata per trovare la posizione di una stella e per calcolare quanto tempo le occorrerà per trovarsi in un certo punto del cielo: ad esempio, se una stella con α = 01h 30m 00s si trova allo zenit, una stella con α = 10h 00m 00s si troverà sulla verticale tra 8 ore e 30 minuti. Qui sotto si può vedere uno schema riassuntivo delle coordinate celesti:
Come esercizio, propongo ai miei lettori di provare a risolvere il triangolo sferico astronomico rappresentato dal già citato triangolo estivo. Di Vega (α Lirae), la stella più luminosa del triangolo, abbiamo già detto che ha una declinazione pari a 38° 47′ 1,291″ = 38°,78369; avendo un'ascensione retta di 18h 36min 56,3364s = 18,61566h, siccome 1h = 180°/12 = 15°, ciò equivale a 279°,23486. Altair (α Aquilae, dall'arabo al-nasr al-ṭāʾir, "l'aquila che vola") ha una declinazione di 8°,86806 e un'ascensione retta di 19h 50min 46,99s = 297°,69579. Infine Deneb (α Cygni, dall'arabo Dhanab ad-Dajājah, "la coda del volatile") ha una declinazione di 45°,28034 e un'ascensione retta di 20h 41min 25,915s = 310°,35798. Provate dunque a determinare l'ampiezza del tre lati VA, AD e DV del triangolo estivo (i vertici sono stati indicati con le iniziali delle rispettive stelle) usando la formula per la distanza di due punti della sfera (io ho trovato VA = 34° 12' 29'', AD = 38° 0' 4'' e DV = 23° 56' 9''). Quindi determinate le ampiezze degli angoli VAD, ADV e DVA, l'eccesso sferico e il rapporto tra l'area del triangolo estivo e quello dell'intera sfera celeste. Secondo i miei calcoli, i tre angoli misurano VAD = 40° 37' 26'', ADV = 64° 45' 16'' e DVA = 81° 57' 8''; l'eccesso sferico è pari a 7° 19' 50'' = 0,1279 radianti, e dunque il rapporto cercato vale 0,1279 R2 / 4 π R2 = 1,02 % della volta celeste (il triangolo estivo racchiude un'area pare a 310 volte circa quella della Luna piena). In tal modo potrete valutare la bontà dei vostri calcoli, e quindi se avete compreso bene i contenuti di questa lezione!
Tutto questo parlare di stelle ci fa venire in mente il libro di Giobbe, laddove il proverbiale paziente si sente rispondere da Dio che Lui solo è il padrone dell'universo e dei fenomeni celesti:
«
Puoi tu annodare i legami delle Plèiadi
o sciogliere i vincoli di Orione?
Puoi tu far spuntare a suo tempo le costellazioni
o guidare l'Orsa insieme con i suoi figli?
Conosci tu le leggi del cielo
o ne applichi le norme sulla terra? » (Giobbe 38, 31-33)
A me però ricorda anche lo stupore di Davide di fronte alle meraviglie della Creazione:
«
Quando vedo i tuoi cieli, opera delle tue dita,
la luna e le stelle che tu hai fissato,
che cosa è mai l'uomo perché di lui ti ricordi,
il figlio dell'uomo, perché te ne curi? » (Salmo 8, 4-5)
Dato che abbiamo dedicato tutta questa lezione alle luminose stelle citate nella Bibbia, non possiamo chiuderla senza far un cenno proprio alla natura della luce, anche se questo è un ipertesto dedicato alla Matematica e non alla Fisica. Com'è noto, nella Genesi essa riveste un ruolo fondamentale, perchè secondo il racconto di Tradizione Sacerdotale fu la prima entità fisica ad essere creata dal Signore:
« Dio disse: "Sia la luce!" E la luce fu. Dio vide che la luce era cosa buona e separò la luce dalle tenebre. Dio chiamò la luce giorno, mentre chiamò le tenebre notte. E fu sera e fu mattina: primo giorno. » (Gen 1, 3-5)
La cosa ha suscitato più di una perplessità tra gli esegeti di ogni tempo, perchè i grandi luminari del cielo, deputati a produrre proprio tale luce, sono creati solo nel quarto giorno dell'Eptamerone!
« Dio disse: "Ci siano fonti di luce nel firmamento del cielo, per separare il giorno dalla notte; siano segni per le feste, per i giorni e per gli anni e siano fonti di luce nel firmamento del cielo per illuminare la terra." E così avvenne. E Dio fece le due fonti di luce grandi: la fonte di luce maggiore per governare il giorno e la fonte di luce minore per governare la notte, e le stelle. Dio le pose nel firmamento del cielo per illuminare la terra e per governare il giorno e la notte e per separare la luce dalle tenebre. Dio vide che era cosa buona. E fu sera e fu mattina: quarto giorno. » (Gen 1,14-19)

Michelangelo Buonarroti, Creazione degli Astri, volta della Cappella Sistina, 1512
Il fatto è che, nella mentalità dell'Autore Sacerdotale, la "luce" creata nel Primo Giorno è in realtà sinonimo di tempo! Infatti Iddio non si limita a creare la luce, la separa dalle tenebre, perchè esse ritmano l'alternarsi stesso dei giorni della Creazione: « E fu sera e fu mattina » (Gen 1, 5.8.13.19.23.31). Senza questo alternarsi non vi sarebbe il tempo, e senza il tempo, al di fuori del quale il Signore vive, la creazione stessa non sarebbe realizzabile. La creazione dello spazio, separando le acque inferiori da quelle superiori per creare l'universo ordinato in mezzo ad esse, avviene infatti solo nel Secondo Giorno. Invece nel Quarto Giorno avviene la creazione degli astri, a loro volta deputati a irradiare di luce la terra dei viventi e a regolare il calendario. Nel Primo Giorno, dunque, Iddio avvia lo scorrere del tempo, mentre nel Quarto lo regola con precise leggi matematiche.
La luce nella Bibbia è segno anche della presenza costante di Dio nella nostra vita:
«
Il Signore è mia luce e mia salvezza:
di chi avrò timore?
Il Signore è difesa della mia vita: di chi avrò paura? » (Salmo 27, 1)
«
Casa di Giacobbe, venite,
camminiamo nella luce del Signore.
» (Isaia 2, 5)
E nel Nuovo Testamento si trasforma in simbolo del nuovo Regno Messianico:
« Ora puoi lasciare, o Signore, che il tuo servo vada in pace, secondo la tua parola, perché i miei occhi hanno visto la tua salvezza, preparata da te davanti a tutti i popoli: luce per rivelarti alle genti e gloria del tuo popolo, Israele. » (Luca 2, 29-32)
« In lui era la vita, e la vita era la luce degli uomini » (Gv 1, 4)
« Di nuovo Gesù parlò loro e disse: "Io sono la luce del mondo; chi segue me, non camminerà nelle tenebre, ma avrà la luce della vita." » (Gv 8, 12)
Ma cosa ci dice la scienza moderna, a proposito della luce? Isaac Newton (1642-1727) suppose che la luce fosse un'insieme di corpuscoli cui non diede nome. Per il principio d'inerzia, tali corpuscoli si muoverebbero di moto rettilineo uniforme, e ciò spiegherebbe la propagazione rettilinea della luce. Gli urti elastici dei corpuscoli sulle superfici spiegherebbero le leggi della riflessione., mentre i colori differenti sarebbero dovuti a diverse forme e dimensioni dei corpuscoli. Newton non riusciva a spiegare la rifrazione della luce se non ammettendo che, passando da un corpo otticamente meno denso a uno otticamente più denso, essi avvertivano una non meglio specificata forza di attrazione, che li faceva avvicinare alla normale. Ma tale forza li accelererebbe, ragion per cui nell'acqua la luce dovrebbe viaggiare più veloce che nell'aria, mentre le misure moderne ci dicono che accade il contrario (la velocità della luce nel vuoto è pari a circa 300.000 km/s, nell'acqua a 225.000 km/s, nel vetro a circa 197.000 km/s e nel diamante a soli 124.000 km/s).
Il fiammingo Christiaan Huygens (1629-1695) suppose invece che la luce sia una perturbazione ondosa. Tutti i fenomeni suddetti venivano allora spiegati molto semplicemente con il Principio di Huygens-Fresnel: ogni punto toccato da un'onda diventa a sua volta sorgente di onde sferiche. Queste onde sferiche inviluppano poi nuovi fronti d'onda A'B' paralleli ai fronti d'onda generatori AB, come mostra lo schema sottostante:
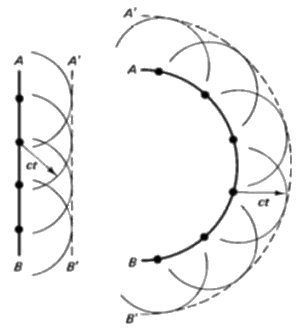
Tuttavia a sfavore di questa teoria così semplice ed elegante giocavano tre fattori:
a) se fosse un'onda, la luce
per propagarsi avrebbe bisogno di un mezzo materiale. Invece può propagarsi
anche nel vuoto, dal Sole alla Terra. I corpuscoli di Newton invece
viaggerebbero anche nel vuoto.
b) nessuno era mai riuscito ad osservare fenomeni di interferenza e
diffrazione
della luce (oggi sappiamo che non si usavano sorgenti coerenti, e l'esperimento
falliva).
c) l'indiscussa statura scientifica di Newton fece prendere il sopravvento al
modello corpuscolare.
Il modello newtoniano ebbe successo fino all'anno 1800, quando l'inglese Thomas Young (1773-1829) ottenne per la prima volta frange di interferenza da due fenditure, usate come sorgenti coerenti.
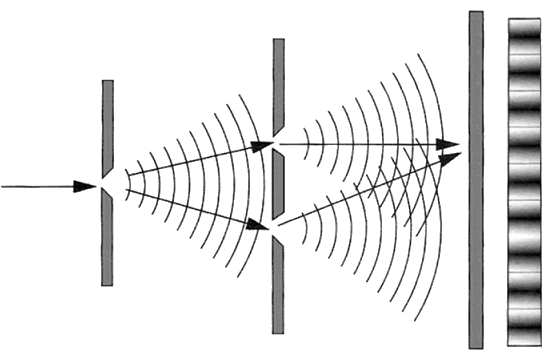
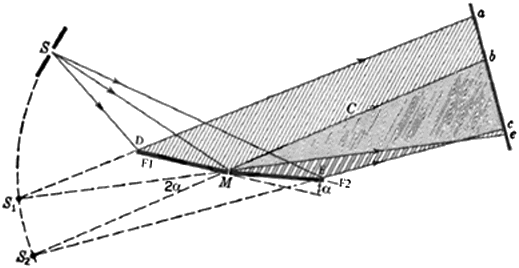
Nel 1818 anche il francese Augustin-Jean Fresnel (1788-1827) ottenne interferenza luminosa usando come sorgenti coerenti due sorgenti virtuali generate da due specchi inclinati l'uno rispetto all'altro. Fu il trionfo del modello ondulatorio, e i corpuscoli di luce finirono in soffitta.
Ma questo modello richiedeva un mezzo in grado di trasmettere le onde luminose. Esso fu individuato nell'etere (dal greco "luminosa"), la "quintessenza" già introdotta da Aristotele, che veniva concepita come un fluido infinitamente trasparente, elastico e sottile che avrebbe permeato tutto l'universo. Il cosiddetto "vuoto" dunque sarebbe stato pieno di etere, permettendo la trasmissione delle onde luminose.
Già Ernst Mach (1838-1916) tuttavia respinse il concetto di etere, inteso come il riferimento assoluto dell'intero universo, considerandolo "metafisico" (come tutto ciò cui si appioppa l'aggettivo "infinitamente"). L'americano Albert Abraham Michelson (1852-1931) e il suo collaboratore Edward Williams Morley (1838-1923), convinti dell'esistenza dell'etere, tentarono di dimostrarla utilizzando un dispositivo di loro invenzione, detto "interferometro", che facendo interferire tra loro diversi raggi di luce misurava la velocità della luce con la precisione del km/s. Essi misurarono la velocità della luce nella direzione del moto della Terra nello spazio e in direzione opposta. Se l'etere esistesse, nel primo caso la velocità della luce si sommerebbe a quella della Terra intorno al Sole (33 km/s), nel secondo caso si sottrarrebbe; l'interferometro di Michelson-Morley è abbastanza sensibile da registrare la differenza attraverso lo spostamento delle frange d'interferenza. Nonostante 25 anni di vani tentativi (prima di entrambi, poi del solo Michelson dopo la morte di Morley), non si riuscì mai a registrare alcuna differenza di velocità. I casi allora sono due: o la Terra trascina con sé l'etere, che però allora non è il riferimento assoluto cercato; oppure, semplicemente l'etere non esiste.
Come spiegare il mistero? Ci riuscì nel 1905 un oscuro impiegato dell'Ufficio Brevetti di Berna, di nome Albert Einstein (1879-1955), il quale dimostrò che la luce è contemporaneamente corpuscolo e onda. In altre parole, è composta da pacchetti di energia detti fotoni (dal greco "phòs", "luce"), i quali si muovono lungo traiettorie ondulatorie. Ma perchè? E come? La risposta sarà fornita dalla Meccanica Quantistica solo negli anni '30 del secolo scorso: ogni particella si comporta contemporaneamente da corpuscolo e da onda. Ma questa è tutta un'altra storia. O meglio, è tutta un'altra fisica.
![]()