![]()
|
« In quei giorni un decreto di Cesare Augusto ordinò che si facesse il censimento di tutta la terra... » (Luca 2, 1) |
Oggi parliamo di censimenti. Quando associamo questa parola alla Bibbia, ci viene subito in mente il famosissimo "primo censimento" dell'Impero Romano ordinato da Cesare Augusto, il quale costrinse Giuseppe a tornare con la sua sposa Maria nella città d'origine della sua famiglia, Betlemme; in tal modo Gesù nacque in questa città, realizzando le antiche profezie, e in particolare quella di Michea. In realtà però di censimenti si parla già nell'Antico Testamento, anzi fin dall'origine stessa del Popolo d'Israele; poco più di due anni dopo la partenza dall'Egitto, infatti, YHWH ordina a Mosè di censire il popolo d'Israele prima che questo si metta in marcia verso la Terra di Canaan:
« Il Signore parlò a Mosè, nel deserto del Sinai, nella tenda del convegno, il primo giorno del secondo mese, il secondo anno dalla loro uscita dalla terra d'Egitto, e disse: "Fate il computo di tutta la comunità degli Israeliti, secondo le loro famiglie, secondo i loro casati paterni, contando i nomi di tutti i maschi, testa per testa, dai vent'anni in su, quanti in Israele possono andare in guerra; tu e Aronne li censirete, schiera per schiera." » (Numeri 1, 1-3)
Il Libro dei Numeri trae il proprio nome giusto dal fatto che i suoi primi quattro capitoli sono occupati dal racconto di tale censimento, con l'elencazione delle cifre esatte dei censiti per ogni tribù; il titolo ebraico invece è "bemidbàr" (במדבר), "nel deserto", perchè si mette piuttosto l'accento sui lunghi anni di peregrinazione degli Ebrei verso la Terra Promessa, che occupano la parte centrale del libro. Dei numeri di questo censimento riparleremo ampiamente in seguito; in ogni caso, si pensa che essi rappresentino invece una "fotografia" del Popolo Eletto in epoca davidica, oppure ancora posteriore. Il totale della popolazione censita è infatti di 603.550 persone (Num 1, 46), donne e bambini esclusi, cifra già riportata in Esodo 38, 26, mentre in Num 26, 51 tale cifra sarà ridotta a 601.730: difficile immaginare che gli Ebrei in viaggio nel deserto verso Canaan fossero così tanti. Questa cifra è compatibile solo con la popolazione del Regno di Israele già consolidato nella sua nuova patria: che la realtà numerica fosse diversa ce lo dice Giudici 5,8, dove sei tribù non riescono a mettere insieme più di quarantamila persone abili alle armi per combattere il potente Iabin, re cananeo di Asor. Evidentemente all'Autore Sacerdotale, cui dobbiamo questa pagina, vissuto al tempo dell'Esilio a Babilonia, premeva mostrare la continuità, anzi quasi l'identificazione, tra quell'antica federazione di clan in peregrinazione nel deserto del Sinai verso una terra promessale dall'Onnipotente e l'Israele a lui contemporaneo, immediato erede del Regno Davidico, e che puntava con fede incrollabile alla restaurazione di quest'ultimo.
Di un altro famoso censimento troviamo menzione nel Secondo Libro di Samuele:
« L'ira del Signore si accese di nuovo contro Israele e incitò Davide contro il popolo in questo modo: "Su, fa' il censimento d'Israele e di Giuda." Il re disse a Ioab, capo dell'esercito a lui affidato: "Percorri tutte le tribù d'Israele, da Dan fino a Bersabea, e fate il censimento del popolo, perché io conosca il numero della popolazione." » (2 Sam 24, 1-2)
Questa volta YHWH sembra incitare il re Davide a censire il popolo d'Israele a scopo di vendetta; e infatti, quando Ioab consegna al Re i risultati del censimento (ottocentomila uomini abili alle armi nel Regno d'Israele e cinquecentomila nel Regno di Giuda), subito Davide di pente della propria scelta. Nonostante questo pentimento, la vendetta del Signore è terribile: « Il Signore mandò la peste in Israele, da quella mattina fino al tempo fissato; da Dan a Bersabea morirono tra il popolo settantamila persone » (2 Sam 24, 15). Sembra una reazione davvero sproporzionata. Non essendoci ancora il Tempio di Gerusalemme, Davide decide di innalzare un altare al Signore nell'aia di Araunà il Gebuseo (ricorda il raddoppiamento dell'ara di Apollo nella lezione da noi dedicata alla duplicazione del cubo): « Davide costruì in quel luogo un altare al Signore e offrì olocausti e sacrifici di comunione. Il Signore si mostrò placato verso la terra e il flagello si allontanò da Israele. » (2 Sam 24, 25) In quello stesso luogo verrà poi edificato il tempio di Salomone. Sembra proprio che l'Autore Deuteronomista utilizzi il censimento del Regno di Davide per giustificare, attraverso l'ira del Signore, la pestilenza che colpì Israele in quell'epoca, pestilenza che presumibilmente nulla aveva a che fare con il censimento, se non il fatto che forse esso comportò un trasferimento massiccio di persone verso i luoghi in cui venivano censite, facilitando la diffusione del contagio. Si noti che il Cronista dà una diversa interpretazione allo stesso episodio: « Satana insorse contro Israele e incitò Davide a censire Israele. » (1 Cr 21, 1) Secondo il Deuteronomista il bene e il male vengono entrambi da Dio, il Cronista invece attribuisce il male al Nemico. Ma, se il censimento era previsto dalla legge di Mosé, perchè Ioab cerca di dissuadere Davide dal bandirlo, ed YHWH si accende d'ira contro Israele al punto da inviare la peste?
Nel Libro dell'Esodo il Signore è stato chiaro con Mosè: « Quando per il censimento conterai uno per uno gli Israeliti, all'atto del censimento ciascuno di essi pagherà al Signore il riscatto della sua vita, perché non li colpisca un flagello in occasione del loro censimento. » (Es 30, 11-12) Nella mentalità orientale, contare qualcosa equivaleva a riaffermare il proprio possesso su di essa, e solo YHWH era il Padrone del Popolo Eletto. Come scrive in proposito la biblista Suor Gloria Riva, « "Chiunque verrà sottoposto al censimento, pagherà un mezzo siclo, che sarà un'offerta prelevata in onore del Signore" (Es 30, 13), per sottolineare la sacralità del censimento in quanto la vita di ogni uomo è nelle mani di Dio. Davide invece vuole il censimento affinché io conosca il numero della popolazione. Davide si abbandona al momento di gloria che sta vivendo a motivo delle sue conquiste, smette di guardare al popolo come a una proprietà di Dio e lo considera oggetto della sua forza e della sua ambizione. »

Maria si presenta al censimento di Quirinio, mosaico nella Chiesa di San Salvatore in Chora a Istanbul
E veniamo al terzo (e più importante) censimento citato nel testo sacro. Stiamo parlando ovviamente del "decreto di Cesare Augusto" che ordinò "il censimento di tutta la terra". Proprio il più importante dei censimenti biblici, tuttavia, pone da sempre problemi agli storici e agli esegeti. Così recita il testo evangelico:
« In quei giorni un decreto di Cesare Augusto ordinò che si facesse il censimento di tutta la terra. Questo primo censimento fu fatto quando Quirinio era governatore della Siria. Tutti andavano a farsi censire, ciascuno nella propria città. Anche Giuseppe, dalla Galilea, dalla città di Nazaret, salì in Giudea alla città di Davide chiamata Betlemme: egli apparteneva infatti alla casa e alla famiglia di Davide... » (Luca 2, 1-4)
Il Quirinio qui citato è Publio Sulpicio Quirinio (45 a.C. - 21 d.C.), prima Proconsole della Provincia di Creta e Cirenaica, e poi Legato in Siria, di cui parlano Tacito negli "Annali" e Cassio Dione nella "Storia di Roma". Ma l'unico censimento svolto da Quirinio in Giudea di cui si ha notizia nelle fonti storiche è citato nelle "Antichità giudaiche" di Giuseppe Flavio, ed ebbe luogo nel 6 d.C., quando Augusto esiliò Archelao, sanguinario figlio di Erode il Grande ed Etnarca di Giudea e Samaria; allora infatti i suoi possedimenti passarono sotto il diretto controllo di Roma e diedero vita alla nuova Provincia di Giudea. Un certo Coponio ne fu il primo governatore, con il rango di prefetto. In quell'anno Quirinio fu nominato legato, cioè governatore della Siria, ed allora egli ebbe il compito di censire i territori di nuova acquisizione, per stimarne la ricchezza in vista della sua tassazione. Il censimento di Quirinio naturalmente contrastava, così come quello di Davide, con il diritto esclusivo da parte di YHWH di contare (e quindi di possedere) il Popolo di Israele, ma di fatto rappresentava anche la sottomissione degli Ebrei a un governatore straniero e la fine dell'indipendenza nazionale; per questo suscitò malcontento tra i Giudei e scatenò la rivolta di Giuda il Galileo, repressa nel sangue (ad essa accenna anche Rabbi Gamaliele negli Atti degli Apostoli: « sorse Giuda il Galileo, al tempo del censimento, e indusse gente a seguirlo, ma finì male, e quelli che si erano lasciati persuadere da lui si dispersero. » Atti 5, 37). Ma nel 6 d.C. Gesù aveva già 12 anni, dunque la cronologia evangelica sembra errata. Per di più il censimento di cui parla Giuseppe Flavio ebbe solo validità locale, non essendo esteso a tutto l'Impero Romano ma alla sola provincia di Giudea.
Molti esegeti contemporanei sono portati a credere che Luca abbia volutamente retrodatato il censimento del 6 d.C. di almeno dodici anni, volendo inquadrare la nascita di Gesù in un contesto universale collegandola ad un « censimento di tutta la terra ». Ad esempio un autorevole commentatore di Luca, Heinz Schürmann (1913-1999), sostiene che « la connessione artificiosa con il censimento di Quirinio metterebbe agli occhi dell'evangelista la nascita di Gesù in rapporto con tutto l'impero: in lui si compirebbe non solo l'attesa dei Giudei ma di tutta la terra. Si apre un orizzonte vasto come il mondo: è affermata l'importanza universale della nascita di Gesù ». Questa opinione va rispettata, tuttavia io trovo stupefacente che sia proprio Luca, il più attento ai dati storiografici nel suo Vangelo, a ricorrere a una simile voluta manipolazione della storia di Israele. Io penso che, se Luca ha collegato la nascita di Gesù ad un censimento, lo ha fatto a ragion veduta, e non per qualche sottile motivo teologico.
Per sbrogliare la matassa, l'unica possibilità è quella di fare riferimento ai testi storiografici in nostro possesso, e il più importante è sicuramente rappresentato dalle "Res gestae divi Augusti", un resoconto redatto dallo stesso imperatore romano Ottaviano Augusto e riguardante le opere che compì durante la sua attività politica. Il testo delle Res gestae fu inciso su lastre bronzo nel Mausoleo di Augusto, ma l'iscrizione originaria è andata perduta. Fortunatamente il testo ci è giunto inciso in latino e in greco sulle pareti del tempio di Augusto e della dea Roma ad Ancyra, allora capitale della Galazia (oggi Ankara, la capitale della Turchia), oltre ad altri frammenti. Ed ecco il passaggio che ci interessa:
« In consulatu sexto censum populi conlega
M. Agrippa egi. Lustrum post annum alterum et quadragensimum fec[i]. Quo lustro
civium Romanorum censa sunt capita quadragiens centum millia et sexag[i]inta
tria millia. ~ Tum [iteru]m consulari com imperio lustrum [s]olus feci C.
Censorin[o et C.] Asinio cos. Quo lustro censa sunt civium Romanorum [capita]
quadragiens centum millia et ducenta triginta tria mi[llia. Et tertiu]m
consulari cum imperio lustrum conlega Tib. Cae[sare filio] m[eo feci,] Sex.
Pompeio et Sex. Appuleio cos. Quo lustro ce[nsa sunt]civ[ium Ro]manorum capitum
quadragiens centum mill[ia et n]onge[nta tr]iginta et septem millia. » (Res Gestae Divi Augusti, capitolo VIII)
« Durante il sesto consolato feci il
censimento della popolazione, avendo come collega Marco Agrippa. Celebrai la
cerimonia lustrale dopo quarantadue anni. In questo censimento furono registrati
quattro milioni e sessantatremila cittadini romani. Poi feci un secondo
censimento con potere consolare, senza collega, sotto il consolato di Gaio
Censorio e Gaio Asinio, e in questo censimento furono registrati quattro milioni
e duecentotrentamila cittadini romani. E feci un terzo censimento con potere
consolare, avendo come collega mio figlio Tiberio Cesare, sotto il consolato di
Sesto Pompeio e Sesto Apuleio; in questo censimento furono registrati quattro
milioni e novecentotrentasettemila cittadini romani. »

Le Res gestae divi Augusti incise sull'Ara Pacis a Roma
Siccome conosciamo con sicurezza la successione dei consoli romani, sulla scorta delle parole dello stesso imperatore è possibile affermare che egli ordinò tre censimenti universali, nel 28 a.C. (quando ancora non era imperatore), nell'8 a.C. e nel 14 d.C. Il censimento dell'8 a.C. è stato identificato da molti con il "primo censimento" di cui parla Luca, sottintendendo che quello del 6 d.C. sarebbe stato il secondo. Tuttavia in questi tre censimenti universali erano censiti i soli cittadini romani dell'impero, e Giuseppe di Nazaret non era né cittadino romano, né suddito dell'impero, visto che viveva nel regno cliente di Erode il Grande. È però altrettanto vero che Augusto indisse anche molti censimenti locali, estesi pure ai regni satelliti di Roma, e la storia ne ha conservato memoria per via delle ribellioni che essi scatenarono, essendo sempre svolti a scopo di tassazione. Non è dunque da escludere che, più o meno contemporaneamente al grande censimento dell'8 a.C., si sia svolto anche un censimento "locale" del Regno di Erode, benché Giuseppe Flavio non ne parli. Il famoso apologeta cristiano Tertulliano (155-220) in "Adversus Marcionem" (4,19,10) ipotizza un precedente mandato di Qurinio in Siria negli anni 8-6 a.C., come reggente della legazione romana, perchè il legato di allora Sanzio Saturnino era impegnato in una dispendiosa guerra contro l'Armenia; molti esegeti a noi contemporanei sposano questa ipotesi, e a sostegno di essa portano la cosiddetta Lapide di Tivoli, così chiamata poiché là venne ritrovata nel settecento. Il frammento, custodito presso il Museo Pio Cristiano dei Musei Vaticani, recita:
«
PRO CONSVL ASIAM PROVINCIAM OPT...
DIVI AVGUSTI ITERVM SYRIAM ET PHO… »
Esso si riferisce quindi ad un secondo mandato ricevuto da una personalità celebre, già Proconsole d'Asia, presso la provincia di Siria al tempo di Augusto; non è certo che in questa iscrizione si parli di Quirinio, ma a partire dal 12 a.C. egli fu proprio Proconsole d'Asia, e di altri maggiorenti che ricoprirono due volte il ruolo di legati di Siria non se ne conosce nemmeno uno. Come facente funzioni di legato, Quirinio potrebbe aver ordinato un censimento amministrativo in Palestina, connesso a un giuramento di fedeltà all'impero e condotto secondo il metodo tribale e non residenziale, un metodo più accettabile per gli Ebrei. Questo « primo censimento » non avrebbe suscitato alcuna rivolta, e per questo non sarebbe stato riportato negli Annali. Quando divenne legato a pieno titolo, Quirinio avrebbe deciso un secondo censimento più generale e sistematico, quello del 6 d.C.; in tal caso Luca avrebbe solo fatto confusione tra il periodo in cui Quirinio era legato a pieno titolo, e quello in cui ne faceva solo le funzioni, nell'anno 7-6 a.C., corrispondente quindi alla nascita di Gesù. Questa soluzione mi sembra la più sensata, e si sa che la spiegazione più semplice di solito è quella giusta.
Naturalmente la pratica del censimento è molto più antica di Quirinio, e persino più antica di Mosè. Già nel terzo millennio a.C. gli Egizi e i Sumeri compivano indagini per misurare la quantità di uomini e beni di cui si poteva disporre in caso di guerra o di carestie. Lo storico romano Tito Livio ricorda un censimento tenutosi nel 465 a.C., cioè agli inizi dell'Età Repubblicana: « In seguito venne fatto il censimento e Quinzio ne celebrò il sacrificio conclusivo. Pare che i cittadini registrati, fatta eccezione per orfani e vedove, ammontassero a 104.714. » (Ab urbe condita libri, Libro III, 1, 3) Sappiamo che Carlo Magno ordinò un censimento nel suo impero, esteso anche al numero complessivo dei vassalli e dei servi della gleba. Il cosiddetto Domesday Book fu invece commissionato nel dicembre del 1085 da Guglielmo il Conquistatore, con l'intento di contare la popolazione presente sul territorio inglese vent’anni dopo l’invasione normanna. Nel XIII secolo si svolgevano rilevazioni periodiche della popolazione nei Comuni italiani: l'enumerazione aveva come oggetto i capifamiglia, elencati nel "libro dei fuochi", così chiamato perché contava i focolari, cioè le unità abitative. La Serenissima Repubblica di Venezia indisse ufficialmente il primo censimento nel 1338, che venne ripetuto periodicamente; nel 1607 venne introdotto l'uso di formulari a stampa, antenati degli odierni questionari. In Canada risale al 1666 la prima enumerazione dei coloni, classificati per sesso, età, condizione occupazionale e stato anagrafico, attuata (personalmente!) da Jean Talon. I primi censimenti demografici, distinti da quelli economici, vennero introdotti con sistematicità nell’amministrazione della cosa pubblica agli inizi del Settecento. Nel 1790 venne introdotto negli Stati Uniti il censimento triennale, avente finalità elettorali, mancando un sistema di anagrafe locale. La pubblicazione nel 1798 delle teorie di Thomas Malthus riguardanti l'incremento delle risorse disponibili in relazione a quelle della popolazione portò ad un notevole incremento degli studi demografici: il primo censimento demografico in Francia risale al 1800, in Inghilterra e Danimarca al 1801, in Irlanda al 1821, in Australia al 1828, in Olanda al 1829, in Svizzera al 1837, in Belgio al 1846, in Nuova Zelanda al 1851, nello Stato Pontificio al 1853, in Grecia al 1856, nel Lombardo-Veneto al 1857, nel Regno di Sardegna al 1858. In Italia il primo censimento ufficiale risale al 31 dicembre 1861, subito dopo l'unità del paese; da allora le tornate censuarie si sono susseguite ogni dieci anni, con le sole eccezioni del 1891, per le difficoltà finanziarie in cui versava il Paese, e del 1941, a causa della guerra. L'ultima rilevazione risale al 9 ottobre 2011, e ha stabilito che la popolazione residente in Italia ammonta a 59.433.744 abitanti. A partire dalla sua fondazione, nel 1926, a occuparsi dei censimenti è l'Istituto Nazionale di Statistica (Istat). Infine, vale la pena di ricordare che fu proprio la necessità di semplificare i lavori di un censimento, quello degli Stati Uniti d'America, ad avviare lo sviluppo della moderna informatica. Questo lo dobbiamo all'ingegnere Herman H. Hollerith (1860-1929) e al medico John S. Billings (1839-1913), che realizzarono la prima macchina calcolatrice a schede perforate, prototipo di tutti i sistemi meccanografici, per eseguire il lavoro di raccolta e tabulazione dei dati anagrafici del censimento americano del 1890: grazie alla loro macchina, 63 milioni di persone e 150.000 comunità minori vennero censite in un solo mese!

I simboli delle Dodici Tribù d'Israele
Come si vede, chi si occupa di censimenti si trova nella necessità di trattare una grande mole di dati sperimentali, ed è per questo che ha bisogno degli strumenti della Statistica. Dopo aver raccolto milioni di dati riguardo gli abitanti di una certa nazione, occorre procedere ad un'analisi statistica dei risultati. Nel caso del primo censimento di Israele effettuato da Mosè poco dopo il passaggio del Mar Rosso, tutti i maschi appartenenti alle Dodici Tribù costituiscono una popolazione statistica: tale termine designa l'insieme di tutti gli individui oggetto dell'indagine, mentre ogni oggetto viene detto unità statistica. Naturalmente l'analisi statistica ha tanto più senso, quanto più alto è il numero delle unità statistiche; vediamo dunque quanti sono i censiti tribù per tribù. In tal modo capiremo subito perchè il quarto libro dell'Antico Testamento è stato intitolato "I Numeri":
«
Come il Signore gli aveva ordinato, Mosè fece il censimento nel deserto del Sinai.
Risultò per i figli di Ruben, primogenito d'Israele, stabilite le loro genealogie secondo le loro famiglie, secondo i loro casati paterni, contando i nomi di tutti i maschi, testa per testa, dai
vent'anni in su, quanti potevano andare in guerra:
censiti della tribù di Ruben quarantaseimilacinquecento.
Per i figli di Simeone, stabilite le loro genealogie secondo le loro famiglie, secondo i loro casati paterni, contando i nomi di tutti i maschi, testa per testa, dai
vent'anni in su, quanti potevano andare in guerra:
censiti della tribù di Simeone cinquantanovemilatrecento.
Per i figli di Gad, stabilite le loro genealogie secondo le loro famiglie, secondo i loro casati paterni, contando i nomi di quelli dai
vent'anni in su, quanti potevano andare in guerra:
censiti della tribù di Gad quarantacinquemilaseicentocinquanta.
Per i figli di Giuda, stabilite le loro genealogie secondo le loro famiglie, secondo i loro casati paterni, contando i nomi di quelli dai
vent'anni in su, quanti potevano andare in guerra:
censiti della tribù di Giuda settantaquattromilaseicento.
Per i figli di Ìssacar, stabilite le loro genealogie secondo le loro famiglie, secondo i loro casati paterni, contando i nomi di quelli dai
vent'anni in su, quanti potevano andare in guerra:
censiti della tribù di Ìssacar cinquantaquattromilaquattrocento.
Per i figli di Zàbulon, stabilite le loro genealogie secondo le loro famiglie, secondo i loro casati paterni, contando i nomi di quelli dai
vent'anni in su, quanti potevano andare in guerra:
censiti della tribù di Zàbulon cinquantasettemilaquattrocento.
Per i figli di Giuseppe: per i figli di Èfraim, stabilite le loro genealogie secondo le loro famiglie, secondo i loro casati paterni, contando i nomi di quelli dai
vent'anni in su, quanti potevano andare in guerra:
censiti della tribù di Èfraim quarantamilacinquecento;
per i figli di Manasse, stabilite le loro genealogie secondo le loro famiglie, secondo i loro casati paterni, contando i nomi di quelli dai
vent'anni in su, quanti potevano andare in guerra:
censiti della tribù di Manasse trentaduemiladuecento.
Per i figli di Beniamino, stabilite le loro genealogie secondo le loro famiglie, secondo i loro casati paterni, contando i nomi di quelli dai
vent'anni in su, quanti potevano andare in guerra:
censiti della tribù di Beniamino trentacinquemilaquattrocento.
Per i figli di Dan, stabilite le loro genealogie secondo le loro famiglie, secondo i loro casati paterni, contando i nomi di quelli dai
vent'anni in su, quanti potevano andare in guerra:
censiti della tribù di Dan sessantaduemilasettecento.
Per i figli di Aser, stabilite le loro genealogie secondo le loro famiglie, secondo i loro casati paterni, contando i nomi di quelli dai
vent'anni in su, quanti potevano andare in guerra:
censiti della tribù di Aser quarantunmilacinquecento.
Per i figli di Nèftali, stabilite le loro genealogie secondo le loro famiglie, secondo i loro casati paterni, contando i nomi di quelli dai
vent'anni in su, quanti potevano andare in guerra:
censiti della tribù di Nèftali cinquantatremilaquattrocento.
Questi furono i censiti, di cui fecero il censimento Mosè e Aronne e i prìncipi d'Israele, dodici uomini: c'era un uomo per ciascun casato paterno.
E tutti i censiti degli Israeliti, secondo i loro casati paterni, dai vent'anni in su, cioè quanti potevano andare in guerra in Israele,
risultarono registrati in tutto seicentotremilacinquecentocinquanta.
Ma i leviti, secondo la loro tribù paterna, non furono registrati insieme con gli
altri. » (Num 1, 19-47)
Questo brano, redatto dalla Tradizione Sacerdotale, è un elenco numerico vero e proprio, che può essere oggetto di indagine statistica. I numeri tramandatici dall'Autore Biblico possono essere tabulati come segue:
| Tribù |
censiti |
Tribù |
censiti |
| Ruben |
46.500 |
Èfraim |
40.500 |
| Simeone |
59.300 |
Manasse |
32.200 |
| Gad |
45.650 |
Beniamino |
35.400 |
| Giuda |
74.600 |
Dan |
62.700 |
| Ìssacar |
54.400 |
Aser |
41.500 |
| Zàbulon |
57.400 |
Nèftali |
53.400 |
Le proprietà delle unità che saranno oggetto della nostra indagine si diranno caratteri. I caratteri possono essere quantitativi o variabili e qualitativi o mutabili, a seconda che essi possano essere espressi tramite numeri oppure no. Ad esempio, il tipo di arma (lancia, spada, mazza...) imbracciata dagli Israeliti abili alla guerra, o il nome del capostipite di ogni famiglia nell'ambito della Tribù, sono caratteri qualitativi; la quantità di vettovagliamenti consumata in un anno da un israelita atto alle armi in un mese, o il numero dei caduti di ogni Tribù nelle varie guerre contro Madianiti, Edoniti o Filistei sono caratteri quantitativi. Inoltre le variabili si distinguono a loro volta in discrete e continue. Le prime possono assumere solo i valori di un insieme che possono essere numerati, cioè posti in corrispondenza biunivoca con l'insieme dei numeri naturali; le seconde invece possono assumere valori qualsiasi. Tipicamente, le variabili discrete sono quelle che risultano da un'operazione di conteggio; ad esempio, il numero dei figli in ogni famiglia israelitica, oppure l'età (avanzatissima) a cui è morto ogni antenato delle singole casate. Le variabili continue invece derivano tipicamente da misurazioni, come quelle che hanno luogo in Fisica. Questo è il caso della superficie dell'appezzamento posseduto da ogni famiglia, o della temperatura massima raggiunta in estate in ogni villaggio della Terra di Canaan. Facciamo un esempio: presa una delle Dodici Tribù, consideriamo come carattere il casato di appartenenza di ciascun membro di essa. Appuntiamoci per esempio sulla Tribù di Giuda, la più numerosa. Il Cronista ci dice: « Figli di Giuda: Er, Onan, Sela; i tre gli nacquero dalla figlia di Sua la Cananea. [...] Tamar, sua nuora, gli partorì Peres e Zerach. Figli di Peres: Chesron e Camul. Figli di Zerach: Zimrì, Etan, Eman, Calcol e Darda; in tutto: cinque. Figli di Carmì: Acar, che provocò una disgrazia in Israele con la trasgressione dello sterminio. Figli di Etan: Azaria. Figli che nacquero a Chesron: Ieracmeèl, Ram e Chelubài... » (1 Cr 2, 3-9) E l'elenco continua per tutti i capitoli 2 e 3 e per metà del 4. Le modalità sono allora: Casa di Peres, Casa di Zerach, Casa di Chesron, Casa di Camul, eccetera (Gesù apparteneva alla "Casa di Davide"): chiaramente si tratta di un carattere di tipo qualitativo. Oppure, si consideri la quantità di grano necessaria al fabbisogno di una famiglia in un anno. La popolazione è costituita dalle varie famiglie, il carattere è quantitativo continuo, e le modalità sono tutti i possibili valori indicati dalla bilancia usata per pesare il grano consumato.

Jose Riiter Von Fuhric, "Giacobbe e Rachele al pozzo", Vienna
Di ogni modalità che può essere assunta da un carattere occorre misurare le frequenze. Si chiama frequenza assoluta il numero di volte in cui quella modalità è stata osservata. Ad esempio, come narrato nei capitoli 29 e 30 della Genesi, dei Dodici Figli di Israele (trascuriamo qui la figlia femmina Dina) sei sono figli di Lia: Ruben, Simeone, Levi, Giuda, Ìssacar e Zàbulon; due sono figli di Rachele: Giuseppe e Beniamino; due sono figli di Zilpa, schiava di Lia: Gad e Aser; e due sono figli di Bila, schiava di Rachele: Dan e Nèftali. Ne consegue che questi numeri rappresentano le frequenze assolute con cui le quattro maternità si presentano nella prole di Giacobbe. Si dice invece frequenza relativa di una modalità il rapporto tra la frequenza assoluta e il totale della popolazione. Nel semplice caso da noi preso in esame, i figli maschi di Israele sono 12 in tutto, per cui la frequenza relativa dei figli di Lia è 6/12 = 1/2, mentre quella dei figli di Rachele, dei figli di Zilpa e dei figli di Bila è 2/12 = 1/6. Si noti poi che 1/2 + 1/6 + 1/6 + 1/6 = 1. Naturalmente la statistica ha senso per numeri più alti di quelli dei rampolli di Giacobbe. Un esempio può essere rappresentato dalla distribuzione della popolazione per fasce di età: in questo sito potete vedere ad esempio tale distribuzione per la popolazione italiana nell'anno 2015.
Ora, supponiamo che l'Autore Sacerdotale del Libro dei Numeri sia stato più pignolo, e ci abbia trasmesso anche la distribuzione della popolazione per fasce di età delle singole tribù in quel censimento. In tal caso, potremmo riempire la seguente tabella:
| Età |
0-20 |
21-40 |
41-60 |
61-80 |
> 80 |
Tot. |
| fa | 13.800 | 17.450 | 22.600 | 15.900 | 4.850 |
74.600 |
| fr | 0,185 | 0,234 | 0,303 | 0,213 | 0,065 | 1 |
| f% | 18,5 % | 23,4 % | 30,3 % | 21,3 % | 6,5 % | 100 % |
Come si vede, la prima riga contiene le frequenze assolute fa della popolazione della Tribù di Giuda nel Censimento di Mosè. Per ricavare le frequenze relative fr basta sommare tutte le frequenze assolute e poi dividere ciascuna di esse per il totale, cioè 176. Moltiplicando ognuna di esse per 100, abbiamo le frequenze percentuali f% (confesso di aver usato i dati in percentuale della popolazione italiana contenuti nel sito suddetto per costruire questa distribuzione fittizia). Di tali frequenze si danno spesso rappresentazioni grafiche, sotto forma di diagrammi a torta, a barre, eccetera. Ecco ad esempio un diagramma a torta che illustra le percentuali della popolazione di Giuda per fasce di età:

Esistono però anche le frequenze cumulate. Cosa sono? Si tratta della somma delle frequenze assolute di tutte le modalità minori o uguali di quella considerata. Per capire di cosa stiamo parlando, consideriamo non più le fasce di età della popolazione della Giudea che abbiamo ipotizzato nell'esempio precedente, ma il numero di parole dell'originale ebraico dei singoli libri del Pentateuco, tratte da questo sito:
|
.Libro |
Gen |
Es |
Lv |
Num |
Dt |
| Parole | 32.046 | 25.957 | 18.852 | 25.048 | 23.008 |
Questo significa che chi legge il Pentateuco, arrivando alla fine della Genesi ha letto 32.046 parole. Chi arriva alla fine dell'Esodo, ha letto altre 25.957 parole, ma dall'inizio del Pentateuco ha letto 32.046 + 25.957 = 58.003 parole. Giunti alla fine del terzo capitolo, quello del Levitico, sono state lette altre 18.852 parole, e quindi dall'inizio sono state lette 32.046 + 25.957 + 18.852 = 76.855 parole; e così via. Queste sono allora le frequenze cumulate (fc):
|
.Libro |
Gen |
Es |
Lv |
Num |
Dt |
| fa | 32.046 | 25.957 | 18.852 | 25.04 | 23.008 |
| fc | 32.046 | 58.003 | 76.855 | 101.903 | 124.911 |
Appare facile intuire come stavolta sia più utile un diagramma a linee, che mostra di quanto "crescono" le frequenze dall'inizio verso la fine del Pentateuco. L'ultimo valore della frequenza cumulata è ovviamente il totale delle parole, cioè l'intera lunghezza del Pentateuco!
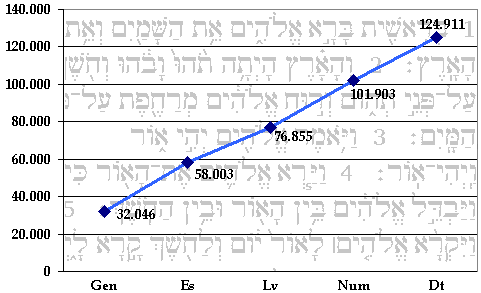
Si noti come, nel censimento di Mosè sopra considerato, la Tribù di Giuda sia quella che presenta la popolazione più numerosa, mentre tra i cinque libri del Pentateuco, la Genesi è quella con il maggior numero di parole. In statistica il dato cui corrisponde la frequenza più alta prende il nome di moda. Tale termine è ispirato a quello del linguaggio comune, nel quale si dice ad esempio che un capo di abbigliamento è alla moda se è portato dalla maggioranza della popolazione. Un altro valore molto importante in statistica è la cosiddetta mediana, definita come segue. Sia una distribuzione di valori che hanno tutti frequenza pari ad 1. Ad esempio, consideriamo le età dei patriarchi antidiluviani contenuti nel capitolo 5 della Genesi, di cui ci siamo occupati nel capitolo dedicato alla cronologia. Nell'ordine da Adamo a Lamec, le loro età sono:
930, 912, 905, 910, 895, 962, 365, 969, 777
Come si vede, nessun numero si ripete. Disponiamo tali valori in ordine crescente:
365, 777, 895, 905, 910, 912, 930, 962, 969
Si definisce mediana di una successione di dati in ordine crescente quello che occupa la posizione centrale. Nel caso da noi esaminato, la mediana è 910, in quanto lascia alla sua sinistra e alla sua destra lo stesso numero di dati. Naturalmente ciò vale e il numero dei dati è dispari; ma se fosse pari? Se aggiungiamo l'età di Noè, cioè 950 anni, la lista diventa 365, 777, 895, 905, 910, 912, 930, 950, 962, 969. In tal caso la mediana è data dalla media aritmetica dei due valori centrali. Essendo 910 e 912 i valori centrali, la mediana diventa 911.
Se i dati della distribuzione presentano frequenze diverse da 1, si potrebbe scrivere ogni dato tante volte quant'è la sua frequenza assoluta ed individuando il termine centrale, ma questo metodo è tutt'altro che praticabile quando si ha a che fare con frequenze molto alte, perchè si dovrebbe lavorare con una fila talora composta di migliaia di numeri; meglio utilizzare la seguente procedura. Consideriamo ad esempio i primi cinque capitoli del libro della Genesi, e contiamo il numero dei loro versetti, inserendoli in una tabella:
| Capitolo |
Versetti |
| 1 | 31 |
| 2 | 25 |
| 3 | 24 |
| 4 | 26 |
| 5 | 32 |
| Totale | 138 |
Calcoliamone le frequenze cumulate con il metodo che abbiamo spiegato poc'anzi:
| Capitoli |
Versetti |
| 1 | 31 |
| 1-2 | 56 |
| 1-3 | 80 |
| 1-4 | 106 |
| 1-5 | 138 |
Ora determiniamo la semisomma del totale delle frequenze, che è 69. La mediana è pari alla modalità cui corrisponde la prima frequenza cumulata che supera tale valore; osservando l'ultima tabella, se ne ricava che la mediana è 3. Tornando al caso delle parole del Pentateuco, la metà della somma totale delle parole dei cinque rotoli è 62.455,5, e tale metà ricade nel libro del Levitico. Nel caso invece che vi sia una somma parziale coincidente con tale semisomma, la mediana è la media tra il valore della modalità corrispondente alla semisomma e il valore della modalità successiva.
Come si vede, trattare decine o addirittura centinaia di valori non è semplice, e non solo per una questione di calcolo, che ai nostri giorni può essere velocizzato facendo uso del supporto informatico, e in particolare del foglio elettronico. Da quella marea di numeri infatti bisogna estrarre dei valori significativi, che "a colpo d'occhio" ne sintetizzino il significato, e per questo sono detti valori di sintesi. In particolare sono stati introdotti i valori di sintesi noti come valori di posizione. Il caso più semplice è rappresentato naturalmente dalla media aritmetica, sulla quale non è il caso di soffermarsi, poiché tutti sappiamo in cosa consiste. Vale piuttosto la pena di precisare i casi in cui la media aritmetica NON è la più adatta da usare per "riassumere" il significato dei dati tabulati. A rendersene conto in maniera magistrale fu il poeta romanesco Trilussa (1871-1950) nel seguente, famosissimo sonetto:
« Sai
ched'è la statistica? È 'na cosa
che serve pe fà un conto in generale
de la gente che nasce, che sta male,
che more, che va in carcere e se sposa.
Ma pe' me la statistica curiosa
è dove c'entra la percentuale,
pe' via che, lì, la media è sempre eguale
puro co' la persona bisognosa.
Me spiego: da li conti che se fanno
seconno le statistiche d'adesso
risurta che te tocca un pollo all'anno:
e, se nun entra nelle spese tue,
t'entra ne la statistica lo stesso
perch'è c'è un antro che ne magna due. »
Si prenda in considerazione in proposito questo esempio. Come si legge nel seguente brano al principio del libro dell'Esodo, i discendenti di Giacobbe in Egitto, partiti dal numero esiguo ma perfetto di 70 (secondo alcuni si tratta del numero totale delle Nazioni della Terra secondo Gen 10), andavano crescendo di giorno in giorno:
« Tutte le persone discendenti da Giacobbe erano settanta. Giuseppe poi morì e così tutti i suoi fratelli e tutta quella generazione. I figli d'Israele prolificarono e crebbero, divennero numerosi e molto forti, e il paese ne fu pieno. [...] Perciò vennero imposti loro dei sovrintendenti ai lavori forzati, per opprimerli con le loro angherie, e così costruirono per il faraone le città-deposito, cioè Pitom e Ramses. Ma quanto più opprimevano il popolo, tanto più si moltiplicava e cresceva, ed essi furono presi da spavento di fronte agli Israeliti. Per questo gli Egiziani fecero lavorare i figli d'Israele trattandoli con durezza. » (Esodo 1, 5-7.11-13)

Busto del Faraone Thutmose IV (Louvre)
Prendiamo in considerazione l'anno 2371 dalla Creazione del Mondo; come abbiamo detto nel capitolo relativo alla cronologia biblica, siamo due anni prima della nascita di Mosè (secondo il Seder Olam Rabbah si tratta del 1389 a.C.). Gli Egiziani (in quell'anno dovrebbe regnare il Faraone Thutmose IV, della XVIII Dinastia) constatano che, rispetto a due anni prima, il numero degli israeliti residenti nella terra di Gosen (una parte del delta orientale del Nilo) è aumentato del 2,3 %. Due anni dopo, nell'Anno dalla Creazione 2373, cioè nel 1387 a.C., il nuovo Faraone Amenhotep III (che a questo punto è « il nuovo re che non aveva conosciuto Giuseppe » di Esodo 1, 8) constata che gli Ebrei crescano di numero del 4,1 % rispetto a due anni prima. Qual è la media delle due crescite?
Una risposta ben poco intelligente sarebbe: del 3,2 %, valore ottenuto sommando 2,3 % e 4,1 %, e dividendo il risultato per due. Infatti, come aveva intuito Trilussa, la definizione di media tra due valori è la seguente: è il valore che avrebbe dovuto essere tenuto durante tutto il periodo di tempo considerato, onde ottenere lo stesso risultato finale. Chiariamo il concetto con un esempio. Rifacciamoci a un noto versetto del Vangelo di Giovanni: « Pietro uscì insieme al discepolo che Gesù amava, e si recarono al sepolcro. Correvano insieme tutti e due, ma l'altro discepolo corse più veloce di Pietro e giunse per primo al sepolcro. » (Gv 20, 3-4) Se il discepolo che Gesù amava corre a 300 metri al minuto per due minuti e a 200 metri al minuto per altri tre, in tutto ha percorso 300 x 2 + 200 x 3 = 1200 metri in cinque minuti, e per ottenere questo risultato avrebbe dovuto procedere per l'intero intervallo di tempo a 1200/5 = 240 metri al minuto; invece la media aritmetica tra 300 m/min e 200 m/min è 250 m/min, e dunque non rappresenta la risposta giusta. Torniamo ora all'esempio dell'incremento demografico di Israele in Egitto. Sia N il numero degli israeliti (ovviamente donne e bambini esclusi, come si usava all'epoca) nell'anno 2369 dalla Creazione. Se due anni dopo tale numero è cresciuto del 2,3 %, ciò significa che il totale rappresenta il 102,3 % del censimento precedente, e quindi può essere indicato con 102,3 x N. Nel 2373 gli israeliti sono cresciuti del 4,1 % rispetto all'anno 2371, e diventano quindi 104,1 volte in più del biennio che precede. Tale numero potrà essere perciò espresso come 102,3 x 104,1 x N. Sia T il tasso di crescita che dovrebbe essere uguale nel 2369-71 e nel 2371-73, affinché si ottenga lo stesso risultato. In base a quanto detto sopra, il numero di Israeliti nel 2373 della Creazione deve essere pari a:
( 1 + T ) x ( 1 + T ) x N = ( 1 + T )2 x N
Da qui si deduce l'equazione:
102,3 x 104,1 x N = ( 1 + T )2 x N
N si semplifica, e si ottiene che ( 1 + T ) è pari alla radice quadrata di 102,3 x 104,1, cioè a 103,2. Ne consegue che il tasso T cercato deve essere pari al 3,2 %. Come si vede, per arrivare a questo risultato l'operazione necessaria non è la media aritmetica, bensì la media geometrica, definita in generale mediante la formula:
![]()
In altri casi, neppure la media geometrica va bene. Ad esempio, se si considerano due resistenze elettriche disposte in serie, la media aritmetica tra di esse è l'operazione corretta per determinare la resistenza media equivalente. Se invece le resistenze sono in parallelo, per trovarne il valore medio occorre eseguirne la media armonica, definita come l'inverso della media aritmetica degli inversi dei valori considerati. Il nome di media armonica è dovuto al matematico greco Archita di Taranto (428-347 a.C.), e deriva dal fatto che le corde vibranti che producono l'accordo perfetto do-mi-sol hanno lunghezze che stanno tra di loro in modo che quella centrale è la media armonica delle altre due. Tale media è molto influenzata dai valori piccoli, mentre la media aritmetica è influenzata piuttosto dai valori grandi.
Un'altra media frequentemente utilizzata è la cosiddetta media pesata (o ponderata), in cui ogni valore entra con un particolare peso, diverso da quello degli altri. In altre parole, ad ogni valore x1, x2, ..., xn è associato rispettivamente un peso f1, f2, ..., fn, in cui la scelta della lettera f rimanda direttamente al concetto di frequenza. La formula che fornisce la media pesata di tali valori è:

Per capirne il significato, si consideri il seguente caso. Supponiamo che la ricchezza media degli abitanti di Gerusalemme, al tempo di Re Acaz (2 Re 16, 1-20; 2 Cronache 28, 1-27; Isaia 7, 1-17), fosse di cento Shekel pro capite, e quella di Emmaus, oggi Amwas, celebre per l'apparizione di Gesù a due suoi discepoli (Luca 24, 13-35), fosse di venti Shekel pro capite. Affermare però che "la ricchezza media delle due città è di sessanta monete pro capite", perchè ( 100 + 20 ) / 2 = 60, è un clamoroso errore che si ritrova persino su quotati quotidiani economici! Il motivo consiste nel fatto che Gerusalemme ed Emmaus non avevano certo la stessa popolazione. Come si è detto, infatti, il valore medio è quello che conserva il totale; calcoliamo dunque questo totale. Si stima che Gerusalemme al tempo di Gesù avesse circa 120.000 abitanti (vedi ad esempio questo sito); supponiamo che Emmaus nella stessa epoca avesse mille abitanti. Ne consegue che la ricchezza totale degli abitanti di Gerusalemme era pari a 100 x 120.000 = dodici milioni di Shekel, mentre quella totale degli abitanti di Emmaus è di 20 x 1000 = ventimila Shekel, per un totale di dodici milioni e ventimila Shekel. Dividendole per la popolazione totale delle due città, cioè 121.000 abitanti, si ottengono 99,34 Shekel a testa. Come si vede, quest'operazione è il risultato di una media pesata, in cui 120.000 abitanti è il peso dei 100 Shekel e 1000 abitanti è il peso dei 20 Shekel. Come si vede, stavolta a dominare è il valore con il peso più importante.
Un altro esempio è il calcolo della temperatura media. Si supponga che a Gerusalemme si registrino 25° di temperatura per 36 giorni all'anno, 26° per 22 giorni all'anno, 27° per 28 giorni all'anno, e così via. Per trovare la temperatura media non basta certo calcolare la media aritmetica delle temperature: occorre infatti moltiplicare ogni temperatura per il corrispondente peso, cioè per il numero dei giorni dell'anno durante i quali essa è registrata, sommare i prodotti e dividere il risultato per i 365 giorni dell'anno. Oggi la media pesata è adoperata ad esempio nei conti correnti bancari, in cui i calcoli vengono fatti attraverso di essa: ad esempio, per 20 giorni sul conto corrente teniamo 12.000 euro, poi depositiamo su di esso 4.000 euro e per 15 giorni teniamo 16.000 euro, quindi preleviamo 1.000 euro e teniamo 15.000 euro per 10 giorni... 20 giorni è il peso di € 12.000, 15 giorni è il peso di € 16.000, 10 giorni è il peso di € 15.000, e così via. La banca calcola la media pesata di tutti questi valori, e fa pagare le tasse su tale media. Anche la speranza di vita alla nascita è il risultato di una media ponderata.
La media aritmetica riveste un particolare valore in Fisica, dove le misure possono essere dirette o indirette. Le prime sono eseguite leggendo direttamente il valore su di uno strumento di misura, ad es. la durata di un fenomeno sul cronometro, o la corrente che attraversa un circuito su di un amperometro. Le seconde invece vanno determinate attraverso calcoli, essendo impossibile il confronto diretto con un'unità di misura: è il caso della misura dell'altezza di una montagna, della distanza in anni luce di una stella da noi, della densità di una sostanza solida. Ora, è facile verificare che, ripetendo innumerevoli volte una misura indiretta, non si ritroverà MAI lo stesso valore, ma i risultati ottenuti saranno distribuiti dentro un intervallo, che di solito viene indicato con la parola inglese range. Ciò è dovuto a due tipi possibili di errori: sistematici e casuali. Gli errori sistematici sono dovuti a cause contingenti, come un cronometro che rimane indietro o uno strumento mal tarato, oppure da difetti della vista dello sperimentatore o dalla sua inesperienza. In genere tali errori sono tutti per eccesso o tutti per difetto; essi possono essere eliminati, sostituendo lo strumento di misura con uno più preciso o lo sperimentatore con uno più esperto. Gli errori casuali (o stocastici) non possono essere eliminati, essendo dovuti per l'appunto ad una distribuzione statistica dei valori attorno ad un valore medio. Ovviamente è più probabile rilevare valori prossimi a questo valore medio, piuttosto che valori eccessivamente piccoli o eccessivamente grandi, per cui la distribuzione di questi valori non è uniforme. Immaginiamo ad esempio di aver misurato l'altezza della Torre di Siloe, quella il cui crollo viene citato da Gesù per insegnare la necessità della conversione:
« O quelle diciotto persone, sulle quali crollò la torre di Sìloe e le uccise, credete che fossero più colpevoli di tutti gli abitanti di Gerusalemme? No, io vi dico, ma se non vi convertite, perirete tutti allo stesso modo. » (Luca 13, 4-5)

La Torre di Davide, presso la Porta di Giaffa a Gerusalemme
Tale altezza è stata ottenuta indirettamente, ad esempio misurando l'ombra della torre, quella di un bastone di lunghezza nota ed eseguendo una proporzione (il metodo che usò Talete da Mileto per determinare l'altezza della piramide di Cheope). Ripetendo 50 volte la misura, si ottengono i seguenti 50 valori in tefahim che, come si è detto nella lezione dedicata alle unità bibliche di misura, sono unità di lunghezza (in italiano "palmi"):
|
275,4 |
258,8 |
279,6 |
318,6 |
303,5 |
|
284,9 |
347,7 |
284,1 |
292,6 |
277,3 |
|
281,0 |
311,1 |
286,9 |
315,2 |
308,7 |
|
308,2 |
291,1 |
275,2 |
299,9 |
272,4 |
|
315,1 |
251,6 |
288,8 |
294,0 |
285,8 |
|
301,6 |
294,9 |
316,7 |
285,0 |
316,2 |
|
309,9 |
258,5 |
305,5 |
295,0 |
260,8 |
|
251,0 |
286,1 |
290,5 |
335,3 |
304,2 |
|
325,3 |
309,1 |
293,9 |
288,0 |
307,8 |
|
269,1 |
294,4 |
308,5 |
332,2 |
278,3 |
Secondo l'autorevole Chazon Ish, un palmo equivale a circa 9,60 cm. Come si vede, il valore più piccolo di questo insieme è 251,0 tefahim (cioè 24,1 m), mentre il massimo è di 347,7 tefahim (cioè 33,4 m). Il loro valore medio è h = ( 275,4 + 258,8 + 279,6 + ... + 278,3 ) / 50 = 296,1 tefahim. Dividiamo ora questi dati in gruppi; nel primo poniamo i valori compresi tra 250 (incluso) e 260 (escluso) tefahim, nel secondo i valori compresi tra 260 (incluso) e 270 (escluso) tefahim, e così via, fino all'ultimo dei dieci gruppi, compreso fra 340 (incluso) e 350 (escluso) tefahim. Al primo gruppo appartengono due valori, al secondo altri due, al terzo sei, al quarto nove, e via discorrendo. Un modo molto comodo per rappresentare questi dati consiste in un istogramma, cioè un grafico che riporta il numero di elementi di ogni gruppo sotto forma di barre verticali affiancate:
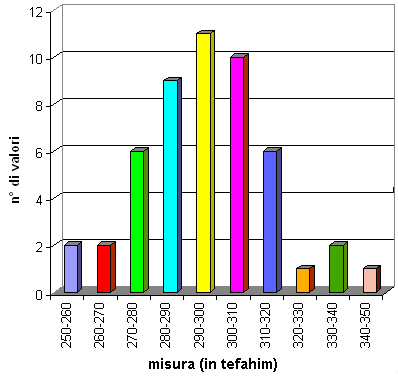
Quando il numero delle misure diventa grandissimo (500, 5000, 50.000...), e quindi anche il numero dei gruppi in cui essi sono suddivisi cresce sempre più, tutte le distribuzioni sperimentali come quella in esame passano dal discreto al continuo, ed assumono sempre la stessa tipica forma a campana, data dalla curva gaussiana, così detta in onore del grande matematico tedesco Carl Friedrich Gauss (1777-1855); di essa parleremo diffusamente nel capitolo dedicato alle distribuzioni di probabilità. Non solo l'errore commesso durante una misura, ma anche l'usura delle parti di un dispositivo meccanico, lo scarto del punto d'impatto di un proiettile rispetto al bersaglio, la lunghezza dei rivetti prodotti da una macchina a controllo numerico, l'altezza e il peso della popolazione di bambini iscritti a una scuola elementare, le variazioni giornaliere dei prezzi di chiusura di un'azione, il tempo che intercorre fra gli arrivi dei voli in un aeroporto, il tempo necessario per servire un cliente in un negozio di abbigliamento, il tempo di caricamento di un sito Internet... sono tutti esempi di grandezze i cui valori rispettano una distribuzione gaussiana. Un caso famoso riguarda il bombardamento di Londra da parte dei nazisti durante la Seconda Guerra Mondiale: una volta una V2 tedesca colpì una caserma, e tra i britannici si diffuse il panico. Possibile che i tedeschi sapessero mirare con tanta precisione da colpire un obiettivo militare a 300 km di distanza? L'analisi dei siti dove erano cadute le V2 tuttavia rivelò che il numero di bombe cadute nei riquadri in cui la mappa di Londra era stata divisa seguiva una distribuzione gaussiana, cioè governata puramente dal caso, e quindi il bombardamento della caserma era stato un evento accidentale.
L'istogramma inoltre mostra chiaramente come la maggior parte delle misure sia compresa tra 270 e 320 tefahim, mentre i valori maggiori di 320 e minori di 270 tefahim siano molto più rari. Inoltre questi valori sono disposti in modo pressoché simmetrico rispetto al valor medio centrale, che dunque rappresenta anche la mediana, cioè il valore che lascia tante misure a destra quante a sinistra. Ciò significa che gli errori per difetto e quelli per eccesso si presentano con la stessa probabilità, e che quindi è corretto considerare come valore più attendibile la media aritmetica dei nostri 50 valori.
I valori di posizione però da soli non bastano, e sarà facile rendersene conto con un esempio. Si considerino i famosi tre servitori della parabola dei Talenti, narrata nel Vangelo Secondo Matteo: « Avverrà infatti come a un uomo che, partendo per un viaggio, chiamò i suoi servi e consegnò loro i suoi beni. A uno diede cinque talenti, a un altro due, a un altro uno, secondo le capacità di ciascuno; poi partì. » (Mt 25, 14-15). Come abbiamo detto nel capitolo dedicato alle unità di misura, nel Nuovo Testamento un talento equivaleva a 58,9 kg, per cui ai tre servi vengono assegnati rispettivamente (e all'incirca) 294, 118 e 59 kg d'oro. Indubbiamente, per gli standard moderni si può tranquillamente affermare che i tre servi erano ricchi sfondati! La media dei loro averi è ( 294 + 118 + 59 ) / 3 = 471 / 3 = 157 kg d'oro. Siano invece altri tre servi, che possiedono rispettivamente sei talenti, un talento e mezzo e mezzo talento, cioè 353, 88,5 e 29,5 kg d'oro. In questo caso il primo è straordinariamente ricco, mentre il terzo è il più povero dei sei servi da noi considerati, eppure la media degli averi degli ultimi tre è ( 354 + 88,5 + 29,5 ) / 3 = 471 / 3 = 157 kg d'oro: la stessa dei primi tre, citati da San Matteo! Le due distribuzioni sono completamente diverse, eppure il loro principale valore di posizione è lo stesso. Per questo sono stati introdotti, oltre ai valori di posizione, anche i valori di variabilità. Essi ci dicono quanto, in media, i valori tabulati si discostano dal valore medio x, cioè dalla media aritmetica dei valori suddetti. Il più semplice di questi valori di variabilità potrebbe essere la media aritmetica delle differenze tra le modalità della variabile x e la loro media x. Tuttavia, basterà un esempio per renderci conto che tale scelta non è la più felice. Consideriamo infatti i tre valori sopra riportati 294, 118 e 59. Sottraendo loro la media 157, si hanno i tre valori + 137, – 39 e – 98, la cui media aritmetica è palesemente ( 137 – 39 – 98) / 3 = 0. E non è una coincidenza: si può dimostrare che la media degli scarti dal valor medio è sempre nulla. E allora?
La soluzione adottata dalla statistica è la seguente. Calcoliamo la media non degli scarti dal valore medio, ma dei loro quadrati; tale risultato è noto come varianza, e la si indica con σ2. Nel nostro caso, ad esempio, si devono elevare al quadrato i tre scarti, ottenendo [ 1372 + ( – 39 )2 + ( – 98 )2 ] / 3 = ( 18.769 + 1.521 + 9.604 ) / 3 = 29.894 / 3 = 9.965. La radice quadrata di questo valore prende il nome di scarto quadratico medio o deviazione standard, lo si indica con σ e nel nostro caso vale circa 100. Questo significa che, in media, i valori della seconda distribuzione di talenti si allontanano di 100 dal valore medio. Proviamo ora con la seconda distribuzione di valori. Sottraendo a 353, 88,5 e 29,5 il loro valore medio 157 si hanno + 196, – 68,5 e – 127,5. Troviamo la varianza: [ 1962 + ( – 68,5 )2 + ( – 127,5 )2 ] / 3 = ( 38.416 + 4.692,25 + 16.256,25 ) / 3 = 59.364,5 / 3 = 19.788, decisamente più elevata del caso precedente. La sua radice quadrata fornisce circa 141; ciò significa che i valori della distribuzione considerata distano in media 141 dal valore medio, cioè molto più della distribuzione precedente! Ciò vuol dire che i patrimoni dei primi tre servi sono tutti addensati intorno al loro valor medio, mentre quelli degli altri quattro si trovano molto più lontani da esso! Ecco come potrebbero apparire le due distribuzioni di talenti, se prendessimo in considerazione ogni volta non tre, ma tremila servitori, e passassimo dal discreto al continuo, rappresentando le distribuzioni assegnate come curve gaussiane:
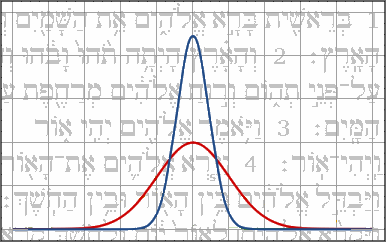
Quella blu è la prima distribuzione, più addensata intorno alla media; quella rossa è la seconda, con i valori mediamente più lontani da x. In pratica, σ è una stima di metà larghezza della distribuzione, ed infatti qualcuno la chiama anche FWHM (Full Width High Middle), ovvero "piena larghezza a metà altezza", perchè tale "mezza larghezza" è valutata a metà dell'altezza del massimo centrale. La formula generale per il calcolo della varianza σ2 è la seguente:

Si può dimostrare che la formula precedente può essere sostituita da questa, più semplice da utilizzare:

Nel primo dei casi da noi usati come esempio, si ha [ ( 2942 + 1182 + 592 ) / 3 ] – 1572 = 9.965. Come si vede, i conti tornano.
Se applichiamo lo stesso metodo alla misura della Torre di Siloe che abbiamo utilizzato sopra, troveremo che in quel caso σ2 = 388 e σ = 19,7. Se la distribuzione è effettivamente gaussiana, si può dimostrare che il 68,3 % delle misure è compreso fra h – σ ed h + σ, cioè nel nostro caso fra 296,1 – 19,7 = 276,4 tefahim e 296,1 + 19,7 = 315,8 tefahim.
Un ruolo importante, nella Statistica, è ricoperto dalle cosiddette Tabelle a Doppia Entrata, che sono alla base della Statistica Bivariata, nella quale si studiano congiuntamente due caratteri X ed Y, allo scopo di mettere in luce eventuali relazioni tra di esse. Un esempio molto semplice è costituito dal seguente. Nel capitolo 6 del Libro dei Giudici si racconta che, dopo quaranta anni di pace seguiti alla vittoria di Debora e Barak contro il re cananeo Iabin, gli israeliti si allontanarono di nuovo dai comandamenti di Dio, che li lasciò alla mercè degli attacchi dei Madianiti e degli Amaleciti. Siccome gli Ebrei si pentirono e invocarono l'aiuto di YHWH, Egli chiamò Gedeone per salvare il popolo e distruggere l'idolatria. Gedeone riunì li uomini della tribù di Manasse, della tribù di Aser, della tribù di Zàbulon e della tribù di Nèftali per combattere gli invasori, in numero di trentaduemila (Giudici 7, 3). L'autore Deuteronomista aggiunge un episodio evidentemente leggendario: onde evitare che il popolo d'Israele possa vantarsi di aver vinto grazie al suo numero e al suo valore, non grazie all'aiuto del Signore, questi ordinò a Gedeone di mandare a casa tutti coloro che si erano messi in ginocchio per bere; restarono solo trecento persone, con le quali Gedeone sgominò i Madianiti e gli Amaleciti, nonostante fossero « numerosi come le cavallette, e i loro cammelli erano senza numero, come la sabbia che è sul lido del mare » (Giudici 7, 12). Naturalmente a combattere furono molte migliaia di Ebrei, altrimenti non avrebbero potuto scacciare gli invasori, neppure con l'espediente dei corni e delle fiaccole narrato in Giudici 7, 16-25. Ma facciamo la tara alle leggende popolari e supponiamo che sia andata proprio così. Immaginiamo che prima dell'ultima scrematura fossero rimasti 1000 soldati delle quattro tribù sopra nominate. Alla fine Gedeone ne mandò a casa altri 700, che non hanno combattuto, e rimasero in 300, che combatterono nella Battaglia della Fonte di Carod alle pendici del Monte Gelboe. Essi potevano essere così distribuiti tra le quattro tribù:
|
Tribù |
Hanno |
Non hanno |
Totale |
|
Manasse |
da Manasse hanno |
da Manasse non |
Manasse |
|
Aser |
da Aser hanno |
da Aser non |
Aser |
|
Zàbulon |
da Zàbulon hanno |
da Zàbulon non |
Zàbulon |
|
Nèftali |
da Nèftali hanno |
da Nèftali non |
Nèftali |
|
Totale |
Ebrei
che |
Ebrei che non |
Ebrei |
Quella che abbiamo costruito qui sopra è una tabella a doppia entrata, perchè i dati entrano dall'alto, distinguendo tra chi ha combattuto e chi no, e anche da sinistra, distinguendo tra le quattro tribù. Ogni coppia di modalità ( X ; Y ) avrà la sua frequenza assoluta, indicata nella tabella. La tabella tuttavia presenta una riga in più, sotto le tre principali, nella quale si inseriscono le somme delle frequenze di ogni colonna, e una colonna in più, a destra delle due principali, nella quale si inseriscono le somme delle frequenze di ogni riga. Tali somme, inserite nei "margini" della tabella, vengono dette frequenze marginali. Essi rappresentano delle "somme parziali", ed i loro significati sono stati scritti dentro le corrispondenti caselle della tabella. In pratica, la colonna sulla destra evidenziata in verde fornisce i numeri dei rappresentanti delle tre tribù prima dell'ultima scrematura, mentre la riga in basso evidenziata in azzurro fornisce il numero totale di quanti hanno combattuto e quanti no. Infine, in basso a destra c'è una cella evidenziata in rosso, nella quale compaiono le somme di entrambe le serie di frequenze marginali. Come si può verificare, entrambe le somme danno come risultato (com'è logico) il numero complessivo di Ebrei seguaci di Gedeone da noi considerato. In pratica, le righe e le colonne marginali forniscono le distribuzioni che si otterrebbero se ciascuno dei due caratteri considerati fosse studiato singolarmente.

|
« Lo spirito del Signore rivestì Gedeone; egli suonò il corno e gli Abiezeriti furono convocati al suo seguito » (Giudici 6, 34. Disegno da "La Sacra Bibbia a Fumetti", ed. San Paolo) |
Se poi consideriamo una sola colonna della tabella soprastante, potremo osservare come il carattere X si distribuisce tra le unità statistiche che manifestano una certa modalità di Y. Ad esempio, la prima colonna ci dice quanti sono i membri delle tribù di Manasse, di Aser, di Zàbulon e di Nèftali che hanno combattuto contro Madianiti e Amaleciti. Si parla in tal caso di frequenze condizionate; condizionate, naturalmente, dalla modalità considerata. Fissare l'attenzione su una singola riga o colonna della nostra tabella significa dunque restringersi alla sottopopolazione che presenta una singola modalità di X o di Y. Tale singola riga o colonna equivale a una distribuzione univariata, per la quale vale tutto il discorso da noi fatto sopra. Da notare che le tabelle a doppia entrata possono essere sostituite con una rappresentazione a diagrammi di Venn, quindi insiemistica. Tutta la statistica anzi può essere riscritta per mezzo della Teoria degli Insiemi.
Lo studio congiunto di due caratteri X ed Y può però essere finalizzato ad uno scopo ben preciso: decidere se fra le due variabili esiste una qualche relazione di dipendenza, cioè se una è funzione dell'altra. A questo scopo, l'idea migliore è quella di confrontare le distribuzioni marginali di X condizionate alle modalità di Y con la distribuzione marginale di X, che esprime il comportamento di X considerato singolarmente. Se le due variabili sono indipendenti tra di loro, c'è da aspettarsi che il condizionamento di X alle modalità di Y non abbia alcun effetto, ovvero che le distribuzioni condizionate si mantengano uguali a quella marginale. C'è però un problema: le frequenze marginali si riferiscono all'intera popolazione, mentre le frequenze condizionate si riferiscono solo alla sottopopolazione relativa alla modalità rispetto alla quale stiamo condizionando. Non dobbiamo dunque lavorare con le frequenze assolute, ma con quelle relative. Diremo perciò che il carattere X è indipendente dal carattere Y se le frequenze relative condizionate di X rispetto alle modalità di Y sono uguali alle frequenze relative marginali di X.
Si può dimostrare che due caratteri X e Y, di cui state osservate le modalità x1, x2, ..., xn e y1, y2, ..., yn su una popolazione costituita da n unità, sono tra di loro indipendenti se e solo se, per ogni i = 1, 2, ..., h e per ogni j = 1, 2, ..., h, si ha:

In pratica, essa equivale a dire che ogni frequenza congiunta deve essere uguale al prodotto delle corrispettive frequenze marginali, diviso per n. Da questo consegue il fatto che la relazione di indipendenza è simmetrica: X è indipendente da Y solo se Y lo è da X. Le frequenze congiunte che soddisfano la condizione di indipendenza sopra scritta vengono chiamate frequenze teoriche di indipendenza, per distinguerle da quelle effettivamente misurate, e le si indica con fT(xi,yj). Ad ogni tabella a doppia entrata è dunque possibile associare una tabella teorica di indipendenza, che si costruisce tenendo fisse le frequenze marginali e sostituendo le frequenze congiunte misurate con quelle teoriche di indipendenza. Se le due tabelle coincidono, allora si ha perfetta indipendenza statistica. Consideriamo a mo' di esempio la tabella vista sopra che esprime la partecipazione delle quattro tribù di Manasse, di Aser, di Zàbulon e di Nèftali alla guerra contro i predoni venuti dal deserto, e costruiamo la tabella delle frequenze teoriche di indipendenza. Ad esempio, la frequenza teorica dei soldati della tribù di Manasse che hanno combattuto al fianco di Gedeone si ottiene moltiplicando il totale dei uomini di Manasse, cioè 150, per il numero totale degli Ebrei che hanno combattuto, cioè 300, e dividendo il prodotto per 1000, che è il totale degli Ebrei prima dell'ultima scrematura. Avremo così 300 x 150 / 1000 = 45, che non coincide con il numero degli uomini di Manasse che hanno effettivamente combattuto. Proseguendo in questo modo avremo la seguente tabella teorica di indipendenza:
|
Tribù |
Hanno |
Non hanno |
Totale |
|
Manasse |
300
x 150 / 1000
= |
700
x 150 / 1000
= |
150 |
|
Aser |
300
x 170 / 1000
= |
700
x 170 / 1000
= |
170 |
|
Zàbulon |
300
x 360 / 1000
= |
700
x 360 / 1000
= |
360 |
| Nèftali |
300
x 320 / 1000
= |
700
x 320 / 1000
= |
320 |
|
Totale |
300 |
700 |
1000 |
Come si vede, nessuna delle otto frequenze teoriche calcolate coincide con la corrispondente frequenza misurata effettivamente, per cui la tabella ora costruita non combacia con quella di partenza, e dunque le due variabili non risultano statisticamente indipendenti. Ciò significa che l'appartenenza a una stirpe piuttosto che all'altra ha una qualche influenza sulla scelta da parte di Gedeone di chi dovrà effettivamente combattere i nemici di Israele, ed infatti le tribù di Zàbulon e di Nèftali hanno visto tornare a casa rispettivamente l'80 % e il 75 % dei loro effettivi, come se il Giudice non si fidasse di loro, mentre di Manasse, che è la tribù di Gedeone, torna a casa solo il 60 % dei soldati. Di Aser, poi, sono più quanti rimangono di quanti partono, come se Ierub-Baal avesse ascoltato la benedizione pronunciata da Mosè prima di morire:
«
Benedetto tra i figli è Aser!
Sia il favorito tra i suoi fratelli
e intinga il suo piede nell'olio.
Di ferro e di bronzo siano i tuoi catenacci
e quanto i tuoi giorni duri il tuo vigore. » (Dt 33, 24-25)
Da notare che, mentre le frequenze rilevate sono sempre espresse da numeri interi, quelle teoriche di indipendenza in generale non lo sono (quello soprastante è stato un caso fortunato), dal momento che scaturiscono da rapporti. Anche però ammettendo che le frequenze teoriche siano tutte espresse da numeri interi, la situazione di perfetta indipendenza statistica è un caso molto raro che si verifica solo raramente, e va quindi considerato come una situazione ideale. Ciò che ci interessa conoscere realmente è: quanto i dati reali si discostano dalla perfetta indipendenza? In altre parole, noi vogliamo conoscere il grado di dipendenza, o meglio di correlazione, come si dice nel linguaggio della statistica, tra due variabili X ed Y. Tale grado sarà tanto più elevato, quanto più la tabella delle frequenze rilevate si discosta da quella delle frequenze teoriche di indipendenza. I principali valori di sintesi che misurano tale scostamento si devono perciò basare sulle differenze tra le frequenze rilevate e quelle teoriche, differenze che vengono chiamate contingenze e sono così definite:
c(xi,yj) = f(xi,yj) – fT(xi,yj)
Si può dimostrare che la somma delle contingenze è sempre pari a zero, come la media degli scarti dal valore medio; per questo, per esprimere con un unico valore di sintesi tutte le differenze, non è possibile limitarsi a sommare le contingenze. Il valore di sintesi più usato è stato introdotto dal matematico britannico Karl Pearson (1857-1936) e, come la varianza e lo scarto quadratico medio, si basa sui quadrati delle contingenze, e viene chiamato "chi quadro" perchè lo si indica con la lettera greca chi (χ):

In pratica, per calcolare il chi quadro occorre determinare tutte le contingenze, elevarle al quadrato e dividerle per le corrispondenti frequenze teoriche di indipendenza, quindi sommare tutti i risultati ottenuti; la doppia sommatoria significa che le somme devono includere gli addendi provenienti da tutte le frequenze congiunte della tabella a doppia entrata. Questo valore di sintesi è pari a zero se e solo se tutte le contingenze sono nulle, cioè se le frequenze teoriche combaciano perfettamente con quelle osservate, e quindi si ha perfetta indipendenza statistica, mentre cresce al crescere delle contingenze. Il valore del chi quadro può essere calcolato più rapidamente usando la seguente formula semplificata, più facile da usare:

In pratica, bisogna elevare al quadrato ogni frequenza congiunta e dividerne il quadrato per il prodotto delle corrispondenti frequenze marginali, sommare tutti i risultati ottenuti, sottrarre uno e moltiplicare il risultato per n. Troviamo ad esempio il valore del χ2 nel caso degli Ebrei che hanno combattuto al comando di Gedeone:
χ2 = 1000 x [ 602/(300 x 150) + 902/(700 x 150) + 902/(300 x 170) + 802/(700 x 170) + 702/(300 x 360) + 2902/(700 x 360) + 802/(300 x 320) + 2402/(700 x 320) – 1 ] = 1000 x [ 0,08 + 0,077 + 0,159 + 0,054 + 0,045 + 0,334 + 0,067 + 0,257 – 1 ] = 1000 x 0,073 = 73
Si presenta ora il problema di interpretare il chi quadro. Il valore ora trovato, 73, è alto o basso? In altre parole, indica l'esistenza di una dipendenza forte o debole? Per rispondere a queste domande occorre "normalizzare" l'indice, cioè trasformarlo in un numero compreso tra 0 e 1, in modo da poterlo interpretare più facilmente. Per far questo, basterà dividere χ2 per il suo valore massimo, cioè il valore che assumerebbe in caso di perfetta correlazione; ma quanto vale, questo valore massimo? Si può dimostrare che tale valore è pari al prodotto tra n, il numero complessivo di unità statistiche considerate, e il minimo tra ( h – 1 ) e ( k – 1 ), dove k ed h rappresentano rispettivamente il numero di modalità differenti dei caratteri X ed Y. Nel caso sopra considerato, k = 4, h = 2 ed n = 1000; tra 4 – 1 = 3 e 2 – 1 = 1 il minimo è rappresentato da 1, per cui il valore massimo di χ2 è pari a 1000 x 1 = 1000. Il χ2 normalizzato perciò vale 73 / 1000 = 0,073 = 7,3 %. Il grado di correlazione tra le quattro tribù di Israele citate in Giudici 6-7 e l'aver partecipato o meno alla guerra contro Madianiti e Amaleciti è appena del 7,3 %: un grado piuttosto basso, almeno nell'esempio da noi ipotizzato.
Un altro valore di sintesi molto usato per valutare la correlazione tra caratteri quantitativi è la cosiddetta covarianza, indicata con il simbolo σXY e così definita:

dove x ed y sono i valori medi di X ed Y. Per capirne il significato, interpretiamola geometricamente. Immaginiamo di rappresentare in un piano cartesiano i punti di coordinate (xi; yi), con i = 1, 2, ..., n. Otterremo una distribuzione di punti, disposti intorno a (x; y); tracciamo le rette x = x ed y = y, cioè le parallele agli assi cartesiani passanti per tale punto. Queste due rette dividono il piano cartesiano in quattro quadranti, che numeriamo in senso antiorario come si vede in figura. Nel quadrante I, i valori di x sono maggiori di x, e quindi si ha x – x > 0, e i valori di y sono maggiori di y, per cui y – y > 0. Il loro prodotto risulterà perciò positivo, e porremo un + nel quadrante. Nel quadrante II, invece, i valori di x sono minori di x, e quindi si ha x – x < 0, mentre i valori di y sono maggiori di y, per cui y – y > 0. Il loro prodotto risulterà perciò negativo, e indicheremo il quadrante con un –. Nel quadrante III, i valori di x sono minori di x, e quindi si ha x – x < 0, ed anche i valori di y sono minori di y, per cui y – y < 0. Il loro prodotto risulta positivo, e indicheremo il quadrante con un +. Infine, nel quadrante IV i valori di x sono maggiori di x, e quindi si ha x – x > 0, mentre i valori di y sono minori di y, per cui y – y < 0. Il loro prodotto è perciò negativo, e indicheremo il quadrante con un –. Per maggior chiarezza:

Se dunque la covarianza è positiva, la maggior parte dei prodotti ( xi – x ) ( yi – y ) è positiva, quindi la maggior parte dei punti di coordinate (xi ; yi) deve cadere nei quadranti I e III; la distribuzione dei punti avrà perciò la forma mostrata nella figura sottostante, e suggerisce una relazione di tipo lineare crescente tra X ed Y:

Se invece la covarianza è negativa, la maggior parte dei prodotti ( xi – x ) ( yi – y ) è negativa, quindi la maggior parte dei punti di coordinate (xi ; yi) deve cadere internamente ai quadranti II e IV; la distribuzione dei punti avrà perciò la forma mostrata nella figura qui sotto, e suggerisce una relazione di tipo lineare decrescente tra X ed Y:

Se invece la covarianza è pressoché nulla, i punti sono sparpagliati senza alcuna regolarità apparente, oppure sono disposti secondo relazioni molto diverse da quella lineare, ad esempio quadratica o logaritmica.
Così come per il chi quadro, anche per la covarianza esiste una formula più semplice da applicare per determinarne il valore:

Anche in questo caso, per stabilire se la correlazione tra X ed Y sia forte o debole occorre normalizzare la covarianza dividendola per il suo valore massimo. In questo caso si può dimostrare che la covarianza di due variabili X ed Y può assumere solo valori compresi entro il seguente intervallo:
![]()
dove σX e σY sono rispettivamente gli scarti quadratici medi di X e di Y. Diremo allora coefficiente di correlazione lineare, o coefficiente di Pearson-Bravais, indicato con ρ, il rapporto:

Per come è stato definito, risulta sempre – 1 < ρ < + 1. Il segno del coefficiente di correlazione lineare è lo stesso della covarianza, e fornisce informazioni analoghe:
ρ > 1 indica una correlazione lineare crescente;
ρ < 1 indica una correlazione lineare decrescente;
ρ = 0 indica l'assenza di una correlazione lineare.
Tanto più ρ è vicino a ± 1, tanto più l'approssimazione con una correlazione lineare è buona, e tanto più i punti corrispondenti ai valori rilevati si addensano lungo una retta; tanto più ρ è prossimo a zero, tanto più i punti se ne discostano. Di solito se 0 < ρ < 0,3 si parla di correlazione lineare debole; se 0,3 < ρ < 0,7, si parla di correlazione lineare media; se 0,7 < ρ < 1, si parla di correlazione lineare forte. Ecco un esempio di alcune distribuzioni di valori con i rispettivi valori di ρ (le prime due sono correlazioni negative, le ultime due positive):

Vogliamo ora vedere un esempio numerico. Torniamo al censimento i cui risultati sono riportati nel primo capitolo del Libro dei Numeri, e ipotizziamo che essi rappresentino anche i numeri delle varie tribù al tempo di Gedeone. In tal caso sappiamo già che la tribù di Manasse comprendeva 32.200 uomini atti alle armi, la tribù di Aser 41.500 uomini, la tribù di Zàbulon 57.400 uomini e la tribù di Nèftali 53.400. Riprendiamo in considerazione anche le truppe tenute con sé da Gedeone per la Battaglia della Fonte di Carod, da noi supposte sopra: 45 da Manasse, 51 da Aser, 108 da Zàbulon e 96 da Nèftali. C'è una correlazione tra la popolazione maschile totale della tribù ed il numero di uomini con cui essa ha contribuito all'armata di Gedeone? Per rispondere a questa domanda, tabuliamo anzitutto i dati che abbiamo appena elencato:
|
.Tribù |
Soldati |
Effettivi |
|
Manasse |
45 | 32.200 |
|
Aser |
51 | 41.500 |
|
Zàbulon |
108 | 57.400 |
|
Nèftali |
96 | 53.400 |
Il numero dei soldati al servizio di Gedeone rappresenterà il carattere quantitativo X, quello totale degli effettivi il carattere quantitativo Y. Per trovare il coefficiente di correlazione tra di essi occorre determinare gli scarti quadratici medi σX e σY e la covarianza σXY di X ed Y. Appare conveniente organizzare i dati in una tabella:
|
xi |
yi |
xi yi |
xi2 |
yi2 |
| 45 | 32.200 | 1.449.000 | 2.025 | 1.036.840.000 |
| 51 | 41.500 | 2.116.500 | 2.601 | 1.722.250.000 |
| 108 | 57.400 | 6.199.200 | 11.664 | 3.294.760.000 |
| 96 | 53.400 | 5.126.400 | 9.216 | 2.851.560.000 |
| 300 | 184.500 | 14.891.100 | 25.506 | 8.905.410.000 |
Nell'ultima riga abbiamo posto le somme di tutte le colonne soprastanti. A questo punto possiamo calcolare tutti i parametri che ci servono:
x = Σ yi / 4 = 300 / 4 = 75
y = Σ xi / 4 = 184.500 / 4 = 46.125
σX2 = Σ xi2 / 4 – x2 = 25.506 / 4 – (75)2 = 751,5
σY2 = Σ yi2 / 4 – y2 = 8.905.410.000 / 4 – (46.125)2 = 98.836.875
σXY = Σ xi yi / 4 – x y = 14.891.100 / 4 – (75 x 46.125) = 263.400
σX è pari alla radice quadrata di 751,5, cioè a 27,41, mentre σY è pari alla radice quadrata di 98.836.875, cioè a 9941,67. Se ne conclude che, nel nostro caso, il coefficiente di correlazione lineare vale:
ρ = 263.400 / ( 27,41 x 9941,67 ) = 0,967
Quindi il numero di soldati e il numero di caduti sono legati al 96,7 % da una correlazione lineare.
Quanto detto però non è sufficiente. Infatti, dopo aver scoperto l'esistenza di una forte relazione lineare tra le variabili X ed Y, vogliamo scrivere la funzione lineare che meglio interpreta tale relazione. Consideriamo dunque una generica funzione lineare di equazione y = m x + q. Per ogni punto Pi(xi,yj) che appartiene alla distribuzione assegnata, consideriamo il corrispondente punto Qi(xi,yj') di ascissa xi come Pi, appartenente alla retta y = m x + q. Tracciamo quindi i segmenti P1Q1, P2Q2, ..., PnQn, ottenendo una figura di questo tipo:
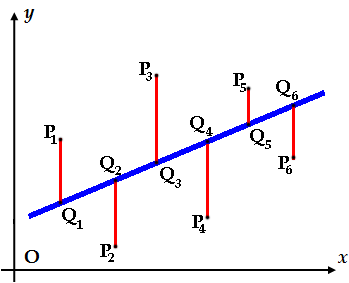
La lunghezza del generico segmento PiQi è pari a |yi – yi'|. Eleviamo al quadrato tali lunghezze e sommiamole, ottenendo Σi ( yi – yi' )2. Questa somma esprime in modo semplice ed efficace una misura dello scarto complessivo fra i dati osservati yi e i valori teorici yi', determinati sul grafico della retta. Come funzione lineare che meglio approssima i dati, scegliamo quella per la quale questa somma Σi ( yi – yi' )2 risulta minima. Questa retta prende il nome di retta di regressione. Si può dimostrare che l'equazione di tale retta è:
y – y = m ( x – x )
Il suo coefficiente angolare m si dice coefficiente di regressione, ed è dato dalla formula seguente:

Determiniamo dunque l'equazione della retta di regressione nel caso dei caduti durante la Battaglia della Fonte di Carod. Già sappiamo che x = 75 e che y = 46.125. Con la formula precedente otteniamo m = 263.400 / 751,5 = 350,5. Abbiamo così l'equazione y – 46.125 = 350,5 ( x – 75 ), cioè:
y = 350,5 x + 19.837,5
Confrontiamo i dati rilevati nella tabella soprastante con quelli generati mediante questa formula:
|
.x |
45 |
51 |
108 |
96 |
| y | 32.200 | 41.500 | 57.400 | 53.400 |
| y' | 35.610 | 37.713 | 57.691,5 | 53.485,5 |
Rappresentata su un opportuno diagramma cartesiano, la retta di regressione nel nostro caso assume questo aspetto:
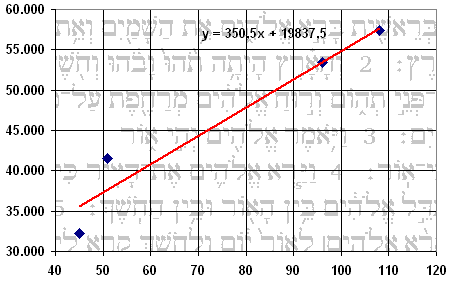
Come si vede, le ultime due "previsioni" sono particolarmente accurate, mentre i valori più bassi sono quelli che più si discostano dai valori teorici. Si noti che la formula ricavata dall'analisi numerica dei dati statistici a nostra disposizione può essere estrapolata al di là di essi, per ottenere previsioni su situazioni analoghe. Ad esempio, supponiamo che Gedeone sia riuscito a tirare dalla sua una quinta tribù, che ha inviato 75 combattenti. Si può prevedere che tale tribù avesse a sua disposizione un numero totale di effettivi ottenuto sostituendo 75 nella retta di regressione determinata, cioè 350,5 x 75 + 19.837,5 = 46.125. Dai dati del censimento di Mosè risulta che la tribù che più si avvicinava a questo numero era quella di Ruben, anche se Gedeone avrebbe indubbiamente faticato parecchio a convincere questa tribù a partecipare alla sua coalizione, dato che essa abitava in Transgiordania e molto più a sud delle altre quattro da lui reclutate. Supponiamo invece che il figlio di Ioas abbia convinto a partecipare la tribù di Ìssacar, stanziata proprio in mezzo fra quelle di Aser, Nèftali, Zàbulon e Manasse, e quindi presumibilmente minacciata dagli stessi nemici. Dal censimento di Mosè risulta che tale tribù poteva contare su 54.400 effettivi, quindi per trovare con quanti uomini in armi essa avrebbe partecipato alla lotta basta risolvere l'equazione 350,5 x + 19.837,5 = 54.400, da cui si ricavano all'incirca 99 uomini. In tal caso, la coalizione di Gedeone avrebbe contato su circa 400 uomini, non su 300. E a chi obietta che 300 = 3 x 10 x 10 è stato scelto essendo il prodotto di tre cifre importantissime nella numerologia biblica, si potrebbe obiettare che 400 furono gli anni trascorsi dagli Israeliti in Egitto secondo Gen 15, 13!

Gedeone guada il Giordano con il
suo esercito, miniatura
del XIV secolo presso la Biblioteca Nazionale di Vienna
Questo tipo di analisi può essere applicato ad un numero inimmaginabile di situazioni; ad esempio, in un elenco di coppie che si sono sposate nello stesso anno in cui si sono sposati Maria e Giuseppe, si può cercare se vi è una correlazione lineare tra l'età della moglie e quella del marito. Oppure, si può verificare se, in una edizione delle Olimpiadi, prendono più medaglie le squadre delle nazioni più popolose, come la Cina, o quelle delle nazioni con il più alto prodotto interno loro pro capite, come Stati Uniti d'America o Germania (in teoria, più abitanti ha un paese, più numerosi possono essere gli atleti e quindi i medagliati, ma se la popolazione più numerosa non può permettersi di andare in palestra ad allenarsi, è difficile ottenere certi risultati). In una classe, può essere fondamentale cercare se vi è una correlazione lineare tra i voti presi da ogni alunno nelle diverse discipline, per verificare se lo studente considerato è selettivo, o ottiene buoni risultati nella maggior parte delle materie. A questo proposito, per correlare tra di loro più di due variabili statistiche si utilizza una matrice di correlazione ρij, una matrice quadrata simmetrica di dimensione n x n che ha sulle righe e sulle colonne le variabili oggetto di studio, e i valori sulla diagonale tutti pari ad 1 (in questo studio però noi non ci addentreremo). Ma soprattutto, questo tipo di analisi dei dati si applica in modo particolare alla fisica, dove è fondamentale scrivere leggi fisiche, anche empiriche, che legano tra di loro le diverse grandezze. Ma questo esula dagli scopi del presente ipertesto.
![]()