

|
"Il vero obiettivo della fisica è quello di giungere a un'equazione che possa spiegare l'universo e che sia abbastanza breve da poter essere scritta su una T-shirt." Leon Lederman |
.
7.1 Pauli e Bohr rivoluzionano la chimica
Come ha letto nel capitolo 6 chi ha conoscenze avanzate di Analisi Matematica (riporto qui una breve sintesi per chi non ne dispone ed è stato costretto a saltare quel capitolo), risolvere l'equazione di Schrödinger (6.4) per l'elettrone che si trova immerso nel potenziale elettrostatico nel nucleo dell'atomo di idrogeno è davvero difficoltoso, ma chi riuscisse ad eseguire tale soluzione (il lettore esperto ne troverà una sintesi nell'Appendice) ricaverebbe da esso tutto quanto già sappiamo a livello empirico, escluso lo spin, come vedremo nel capitolo 8. Il risultato più importante consiste nel fatto che, al posto delle orbite quantomeccaniche previste da Bohr e Sommerfeld, troverebbe delle funzioni d'onda che obbediscono alle leggi di quantizzazione da noi già viste per l'energia, il momento angolare e il momento magnetico. Tali funzioni d'onda prendono il nome di orbitali, e rappresentano delle distribuzioni di probabilità, cioè delle zone dello spazio in cui è più probabile trovare l'elettrone. Per questo il nuovo modello atomico che emerge dalla Meccanica Ondulatoria è chiamato modello ad orbitali. Ecco una sintesi del lungo cammino che portò alla formulazione di tale modello, andata in onda nei lontani anni Ottanta; si tratta di un cartone animato del grande disegnatore italiano Bruno Bozzetto (1938-), andato in onda nell'ambito del programma "Quark" di Piero Angela, e sono sicuro che piacerà anche a voi:
Ma il modello ad orbitali non si limita ad insegnarci quanto già sappiamo per altra via. Infatti da esso emerge in maniera naturale una delle principali proprietà dell'atomo stesso, che fu evidenziata per la prima volta nel 1925 da Wolfgang Pauli (1900-1958): proprio per la sua scoperta il fisico viennese ricevette il Premio Nobel per la Fisica nel 1945. Questo grande uomo di scienza, che a vent'anni si era già messo in luce scrivendo un trattato completo sulla Relatività, pose le basi per una vera rivoluzione della chimica formulando il celeberrimo:
PRINCIPIO DI ESCLUSIONE: due elettroni nello stesso atomo non possono avere tutti e quattro i numeri quantici uguali.
Questo principio ci permette di conoscere come gli elettroni si collocano all'interno di un atomo, il che è fondamentale per capire come interpretare la struttura della materia. Infatti esso ci dice quanti elettroni può contenere al massimo una shell atomica. Nella shell di numero n ho al massimo n orbite, perché:
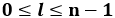
ma ogni orbita ha in tutto ( 2 l + 1 ) possibili orientazioni, giacché:
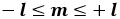
ed ognuna di esse contiene al massimo due elettroni, con spin antiparalleli (esistono solo due stati di spin). Dunque, per ogni orbita ho al massimo 2 ( 2 l + 1 ) elettroni, e dunque nella shell con n fissato è contenuto un numero di elettroni pari a:
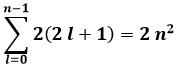
Infatti la somma dei primi n numeri dispari è pari ad n2, come dimostra questo schema:

È logico che gli atomi comincino il "riempimento" degli atomi, cioè quello che con termine tedesco si chiama l'aufbau atomico, a partire dai livelli di energia inferiore, cioè quelli per cui l'energia dell'atomo risulta minima; ogni altra distribuzione possibile rappresenta uno stato eccitato. Inoltre, il comportamento chimico degli atomi dipende solo dal numero di elettroni presenti nel livello più esterno, detto livello di valenza. Allora si può dire che:
1) il livello energetico o shell K, con n = 1, può contenere una sola orbita, con l = 0, che Sommerfeld riteneva perfettamente circolare, ed indicò con la lettera s; esso può dunque contenere al massimo due elettroni.
2) il livello energetico L, con n = 2, può contenere due orbite, con l = 0 ed l = 1; la prima secondo Sommerfeld sarebbe circolare e la seconda ellittica, ed egli indicò quest'ultima con la lettera p. Ne consegue che la shell L può contenere solo le orbite s e p, e questo equivale ad otto elettroni. Di conseguenza un atomo dotato di shell K ed L può contenere al massimo dieci elettroni.
3) il livello energetico M, con n = 3, può contenere tre orbite, con l = 0, l = 1 ed l = 2; le prime due sono le già citate s e p, mentre la terza secondo Sommerfeld sarebbe un'altra orbita ellittica con eccentricità maggiore, indicata con la lettera d. Ne consegue che la shell M può contenere le orbite di tipo s, p, d, e dunque di elettroni ne può contenere al massimo 18. Un atomo con le shell K, L, M può avere non più di 10 + 18 = 28 elettroni.
4) il livello energetico N, con n = 4, può contenere quattro orbite, con l = 0, l = 1, l = 2 ed l = 3; le prime tre sono le già citate s, p e d, mentre la quarta secondo Sommerfeld sarebbe un'ulteriore orbita ellittica con eccentricità ancora più pronunciata, indicata con la lettera f. Ne consegue che la shell N può contenere le orbite di tipo s, p, d, f., per un totale di 32 elettroni. Le orbite K, L, M, N permettono dunque di collocare fino a 28 + 32 = 60 elettroni.
Le orbite con l pari a 4, 5 e 6 sarebbero indicate con le lettere g, h ed i. Attualmente in natura non sono noti elementi con elettroni in queste orbite; tuttavia un elettrone eccitato, per esempio per mezzo di una radiazione elettromagnetica, può andare ad occupare una configurazione orbitale definita da l maggiore di 3. Essi sarebbero riempiti come mostra la tabella seguente, in cui nO è il numero massimo di orientazioni per ogni shell, nS è il numero massimo di elettroni per shell e nTOT è il numero totale di elettroni:
|
Shell |
n |
numero orbitali |
nO |
nS |
nTOT |
|
K |
1 |
1 (s) |
1 |
2 |
2 |
|
L |
2 |
2 (s, p) |
3 |
8 |
10 |
|
M |
3 |
3 (s, p, d) |
5 |
18 |
28 |
|
N |
4 |
4 (s, p, d, f) |
7 |
32 |
60 |
|
O |
5 |
5 (s, p, d, f, g) |
9 |
50 |
110 |
|
P |
6 |
6 (s, p, d, f, g, h) |
11 |
72 |
182 |
|
Q |
7 |
7 (s, p, d, f, g, h, i) |
13 |
98 |
280 |
L'Aufbau atomico segue inoltre altre due regole:
1) in condizioni normali, gli
elettroni di un atomo occupano sempre i livelli energetici per cui l'energia
dell'atomo risulta minima;
2) gli elettroni in un atomo tendono a disporsi con il numero
massimo possibile di spin paralleli tra di loro. Quest'ultima è nota
come regola di Hund, in onore del fisico tedesco Friedrich Hund
(1896-1997).
La shell K contiene al massimo UN'orbita, che nel modello di Bohr-Sommerfeld risulta avere simmetria circolare, mentre nel modello quantistico ad orbitali ha la simmetria sferica illustrata qui sotto, ed infatti ha una sola possibile orientazione spaziale. Tale orbitale in teoria si estende sino all'infinito, perchè solo all'infinito la probabilità di trovare l'elettrone diventa zero. Di solito nella notazione di Sommerfeld lo si chiama 1s, dove 1 indica il valore del numero quantico n ed s quello del numero quantico l, e in quella di Pauli con ( 1 ; 0 ; 0 ).

Dunque, nel livello K si ha n = 1, quindi l può valere solo 0 ed m a sua volta può valere solo 0. Come visto, la shell K contiene un solo orbitale, che nella notazione di Sommerfeld indicheremo con 1s, e in quella di Pauli con ( 1 ; 0 ; 0 ). Il numero di elettroni in esso contenuto viene posto in apice: 1s1 rappresenta così la struttura elettronica dell'idrogeno (Z = 1), e 1s2 quella dell'elio (Z = 2). Questi due sono gli unici elementi che di possono formare con elettroni nel solo livello K:
Questi due elementi vennero allora collocati da Bohr nella prima riga in alto della Tavola Periodica, che contiene gli atomi in grado di riempire al massimo la shell K. Per andare oltre, bisogna cominciare a riempire la shell L. Qui n = 2, quindi l = 0 o l = 1. Il valore di l = 0 per n = 2 mi dà l'orbitale 2s,che può alloggiare due elettroni. Cominciamo con l'orbitale indicato da Sommerfeld con 2s e da Pauli con ( 2 ; 0 ; 0 ), dando per scontato che 1s sia già pieno. Avremo un atomo con tre elettroni e un altro con quattro, che corrispondono al litio (Z = 3) e al berillio (Z = 4):
Il litio ha struttura 1s2 2s1, il berillio 1s2 2s2. Se vogliamo andare oltre, dobbiamo riempire gli orbitali con n = 2 ed l = 1, cioè 2p. Esso nel modello ad orbitale ha la curiosa forma illustrata qui sotto, a due lobi, che possono presentare tre orientazioni spaziali, poiché l vale 1 ed m può assumere tre valori possibili: – 1, 0 e + 1. Si noti che l'elettrone passa da un lobo all'altro attraverso il nucleo per effetto tunnel, un fenomeno che non può avere luogo in un contesto classico, ma solo in un mondo dominato dalla meccanica quantistica, e del quale abbiamo parlato in un paragrafo del capitolo precedente.

Questi orbitali possono alloggiare al massimo sei elettroni, che corrispondono a sei elementi chimici successivi. Secondo la regola di Hund, andrà prima un elettrone con spin up in 2px, poi uno con spin up in 2py, e infine uno con spin up in 2pz, in modo che i tre nuovi elettroni abbiano tutti gli spin paralleli tra di loro:
Abbiamo così il Boro (Z = 5), il Carbonio (Z = 6) e l'Azoto (Z = 7). Successivamente riempiremo i tre posti mancanti con tre elettroni dotati di spin down, e le configurazioni elettroniche dei nuovi atomi saranno le seguenti:
Questi sono rispettivamente l'Ossigeno (Z = 8), il Fluoro (Z = 9) e il Neon (Z = 10). Si noti che quest'ultimo, come l'elio, ha il livello più esterno assolutamente pieno, e quindi non può formare assolutamente legami con altri atomi; per questo si parla di gas nobili (anche i nobili di una volta non volevano mescolare il loro sangue con quello dei plebei). Le loro strutture elettroniche sono:
Boro 1s2 2s2 2p1
Carbonio 1s2 2s2
2p2
Azoto 1s2 2s2
2p3
Ossigeno 1s2 2s2
2p4
Fluoro 1s2 2s2
2p5
Neon 1s2 2s2
2p6
Questa notazione prende il nome di nomenclatura ad apici o nomenclatura spettroscopica, perchè furono gli spettroscopisti ad introdurla, ovviamente ignorandone il vero significato.
Così la shell L è chiusa; bisogna passare alla M. Essa ha n = 3, per cui può contenere l'orbitale con l = 0, indicato da Sommerfeld con 3s e da Pauli con ( 3 ; 0 ; 0 ), quelli con l = 1, indicati da Sommerfeld con le notazioni 3px, 3py, 3pz e da Pauli con ( 3 ; 1 ; – 1), ( 3 ; 1 ; 0 ) e ( 3 ; 1; 1 ), e quelli con l = 2. Gli orbitali d, che nei livelli K ed L non esistono, hanno una struttura a quattro lobi, che possono assumere cinque configurazioni spaziali, poiché l vale 2 ed m può assumere cinque valori possibili: – 2, – 1, 0, + 1 e + 2. Anche in questo caso, l'elettrone passa da un lobo all'altro per effetto tunnel. Si noti che in una delle cinque configurazioni, due lobi sono sostituiti da un anello, mentre in un'altra due lobi hanno forma diversa da quella degli altri due:

3s come visto può contenere al massimo due elettroni, e 3p altri sei, contenendo tre orbitali. Avremo così otto nuovi elementi, il cui riempimento è assolutamente analogo a quelli del livello L:
Si tratta del Sodio (Z = 11), del Magnesio (Z = 12), dell'Alluminio (Z = 13), del Silicio (Z = 14), del Fosforo (Z = 15), dello Zolfo (Z = 16), del Cloro (Z = 17) e dell'Argon (Z = 18). Le loro strutture elettroniche risultano:
Sodio
(Ne) 3s1
Magnesio (Ne) 3s2
Alluminio (Ne) 3s2 3p1
Silicio (Ne) 3s2 3p2
Fosforo (Ne) 3s2 3p3
Zolfo (Ne) 3s2 3p4
Cloro (Ne) 3s2 3p5
Argo (Ne) 3s2 3p6
La scrittura (Ne) indica la configurazione elettronica del neon, cioè 1s2 2s2 2p6: per evitare formule assurdamente lunghe, ci si riporta sempre al gas nobile immediatamente precedente. A questo punto però non si riempie l'orbitale 3d, come ci aspetteremmo, bensì prima il 4s, in base alla regola secondo cui sono riempiti prima gli orbitali con energia minore, e si può verificare che il 4s ha energia minore degli orbitali 3d. Ne consegue che si ottengono gli elementi noti come Potassio (Z = 19) e Calcio (Z = 20), che vanno collocati rispettivamente sotto il sodio e sotto il magnesio:
Le loro strutture elettroniche risultano rispettivamente:
Potassio
(Ar) 4s1
Calcio (Ar) 4s2
Se a questo punto pensate che vengano riempiti i tre orbitali 4px, 4py e 4pz, sono costretto a smentirvi, perchè essi hanno energia superiore al 3d. Tocca dunque prima a quest'ultimo. Esso però può assumere ben cinque configurazioni spaziali, perchè ad l = 2 corrispondono cinque possibili valori di m: – 2, – 1, 0, + 1, + 2. Ne consegue che 3p contiene in realtà cinque orbitali, indicati da Pauli con le notazioni ( 3 ; 2 ; – 2 ), ( 3 ; 2 ; – 1 ), ( 3 ; 2 ; 0 ), ( 3 ; 2 ; 1 ) e ( 3 ; 2 ; 2 ). In tutto essi possono contenere 10 elettroni, per un totale di 10 nuovi atomi:
I nuovi elementi così prodotti sono lo Scandio (Z = 21), il Titanio (Z = 22, vedi più sotto), il Vanadio (Z = 23), il Cromo (Z = 24), il Manganese (Z = 25), il Ferro (Z = 26), il Cobalto (Z = 27), il Nichel (Z = 28), il Rame (Z = 29) e lo Zinco (Z = 30). Questi elementi vengono detti metalli di transizione o metalli del blocco d; essi hanno una resistenza meccanica molto alta, punti di fusione ed ebollizione piuttosto alti e buona conducibilità elettrica e termica, a causa della capacità degli elettroni dell'orbitale 3d di delocalizzarsi e viaggiare liberamente lungo il reticolo cristallino dei metalli. Le loro strutture elettroniche risultano:
Scandio
(Ar) 3d1 4s2
Titanio (Ar) 3d2 4s2
Vanadio (Ar) 3d3 4s2
Cromo (Ar) 3d4 4s2
Manganese (Ar) 3d5 4s2
Ferro (Ar) 3d6 4s2
Cobalto (Ar) 3d7 4s2
Nichel (Ar) 3d8 4s2
Rame (Ar) 3d9 4s2
Zinco (Ar) 3d10 4s2
Vi sono in realtà alcune irregolarità, dovute all'energia totale dell'atomo. Per esempio, il rame in realtà ha struttura . Comunque, subito dopo lo zinco si riempiono i tre orbitali 4px, 4py e 4pz, dando vita ad altri sei elementi:
Abbiamo così ottenuto il Gallio (Z = 31), il Germanio (Z = 32), l'Arsenico (Z = 33), il Selenio, (Z = 34), il Bromo (Z = 35) e il Kripton (Z = 36). Quest'ultimo è un gas nobile, perchè la configurazione elettronica esterna è completa. Le loro strutture elettroniche risultano:
Gallio
(Ar) 3d10 4s2 4p1
Germanio (Ar) 3d10 4s2
4p2
Arsenico (Ar) 3d10 4s2
4p3
Selenio (Ar) 3d10 4s2
4p4
Bromo (Ar) 3d10 4s2
4p5
Kripton (Ar) 3d10 4s2
4p6
Poi non si riempie 4d, come ci si aspetterebbe, bensì 5s; segue 4d, poi 5p, e così via fino allo xeno. In seguito però non si riempie 5d, bensì 6s. A questo punto non si riempie ancora 5d, bensì 4f, che ha energia inferiore. L'orbitale f ha una complicata struttura a sei lobi, che possono assumere sette configurazioni spaziali, poiché l vale 3 ed m può assumere sette valori possibili: – 3, – 2, – 1, 0, + 1, + 2 e + 3, ma per semplicità non ne forniamo tutte le possibili rappresentazioni tridimensionali. I sette orbitali 4f si riempiono con ben 14 elettroni, dopodichè si ha finalmente 5d, e poi 6p e 7s. A questo punto si riempie 5f prima di 6d, e qui si interrompe la catena perché, nonostante gli sforzi dei Fisici Nucleari, a tutt'oggi non sono noti elementi con elettroni in altri orbitali. Qui sotto si può vedere un diagramma energetico che mostra qual è la successione di energie crescenti dei vari orbitali; gli elettroni riempiono via via quelli di energie crescenti, esattamente come un uomo sale una scala un piolo dopo l'altro, senza saltarne alcuno!
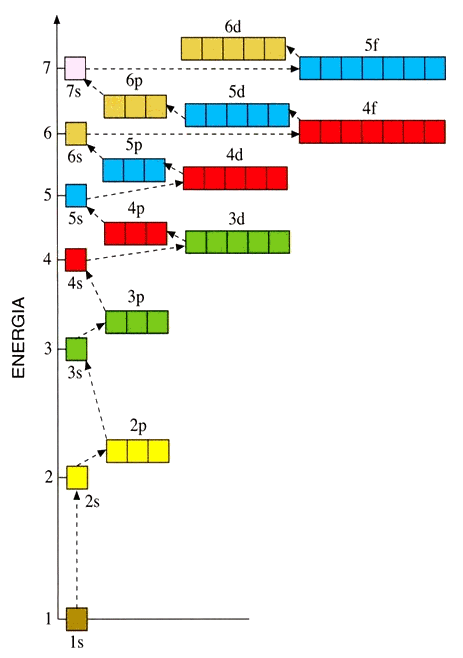
L'immagine sottostante, nella quale si vede anche il grande Wolfgang Pauli, mostra le possibili forme "reali" dei vari orbitali nelle prime cinque shell elettroniche:

.
7.2 Una nuova tavola periodica
Quanto fin qui esposto suggerisce i risistemare in modo nuovo gli elementi chimici, già ordinati nel 1869 dal russo Dmitrij Ivanovič Mendeleev (1834-1907) in base a proprietà puramente macroscopiche, e precisamente in ordine di masse molari crescenti. Fin dal 1921 Niels Bohr si era reso conto che le periodicità della tavola degli elementi dovevano riflettere la costruzione degli atomi a livello elettronico, pur senza ancora conoscere il Principio di Esclusione di Pauli. Infatti, a parte un elettrone in più, la struttura di ogni atomo è identica a quella dell'atomo che lo precede nel sistema periodico. Allora gli elementi possono essere ordinati per numero atomico Z, anziché per massa molare (cioè per massa atomica). La loro disposizione secondo Bohr è però diversa da quella originariamente prevista da Mendeleev, che potete vedere qui sotto:

Secondo Bohr, Z rappresenta in sostanza il grado di riempimento delle shell elettroniche, come dimostrano le notazioni ad apici introdotte nel paragrafo precedente. Gli elementi che fanno parte della stessa colonna hanno la stessa struttura elettronica esterna, e quindi le stesse proprietà chimiche. Per esempio l'ossigeno, che secondo la notazione spettroscopica ha struttura 1s2 2s2 2p4, mentre lo zolfo ha struttura 1s2 2s2 2p6 3s2 3p4. Lo strato di valenza ha comunque struttura , per cui è logico che essi "si somiglino" dal punto di vista chimico e vadano messi l'uno accanto all'altro. Così, tutti gli elementi nella prima colonna a sinistra della tavola periodica di Bohr, come idrogeno, litio e sodio, hanno la struttura esterna xs1, e si dicono alcalini (dalla parola araba Al Qali, che indica la soda caustica o idrossido di sodio). Gli elementi della seconda colonna da sinistra, come berillio e magnesio, hanno tutti struttura esterna xs2, e sono i cosiddetti elementi alcalino-terrosi. Tutti gli elementi della penultima colonna sulla destra, come fluoro e cloro, hanno struttura esterna xs2 xp7 e fanno parte dei cosiddetti alogeni (in greco "generatori di sali"), con valenze 1, 3, 5 e 7. L'ultima colonna sulla destra contiene elementi con struttura esterna , e si dice che hanno l'ottetto esterno completo. Pur non avendo la shell completa (ciò succede solo per elio e neon), hanno completi gli orbitali che contengono elettroni, e dunque possiedono una struttura molto stabile. Avendo la struttura elettronica completa, essi hanno valenza zero e si dicono gas nobili per analogia con gli aristocratici, che non hanno relazioni con i plebei (se ne conoscono con sicurezza sette: elio, neon, argo, xeno, kripto e radon).
Partiamo dalla shell K, che avendo n = 1, e quindi l = 0 ed m = 0, contiene un solo orbitale, chiamato da Sommerfeld 1s, e indicato da Pauli con la notazione ( 1 ; 0 ; 0 ). Ad esso corrispondono due soli elementi: idrogeno ed elio, come si è visto sopra, che Bohr collocò nella prima riga della sua nuova tavola periodica. Passando alla shell L, essa ha n = 2, quindi l può avere due valori, 0 o 1. Il primo corrisponde all'orbitale indicato da Sommerfeld con 2s e da Pauli con ( 2 ; 0 ; 0 ), mentre il secondo a 2p. 2s come visto può contenere al massimo due elettroni, mentre 2p può assumere tre configurazioni spaziali, perchè ad l = 1 corrispondono tre possibili valori di m: – 1, 0, + 1. Ne consegue che 2p contiene in realtà tre orbitali, indicati da Sommerfeld con le notazioni 2px, 2py, 2pz e da Pauli con ( 2 ; 1 ; – 1), ( 2 ; 1 ; 0 ) e ( 2 ; 1; 1 ). In tutto la shell K contiene dunque quattro orbitali, per un totale di 8 elettroni, e quindi di 8 nuovi atomi che, come abbiamo visto nel paragrafo precedente, sono nell'ordine litio, berillio, boro, carbonio, azoto, ossigeno, fluoro e neon.
Trasferiamoci ora nella shell M. Riempiendo l'orbitale 3s, cioè ( 3 ; 0 ; 0 ), abbiamo gli elementi sodio e magnesio, mentre riempiendo gli orbitali 2px, 2py, 2pz, indicati da Pauli con le scritture ( 3 ; 1 ; – 1), ( 3 ; 1 ; 0 ) e ( 3 ; 1; 1 ), otteniamo nell'ordine i sei elementi alluminio, silicio, fosforo, zolfo, cloro e argon. Ciascuno di questi sei elementi ha la stessa configurazione elettronica esterna degli otto 2s e 2p che vanno dal litio al neon, e così Bohr dispose il sodio sotto il litio, il magnesio sotto il berillio, l'alluminio sotto il boro, il silicio sotto il carbonio, il fosforo sotto l'azoto, lo zolfo sotto l'ossigeno, il cloro sotto il fluoro e l'argon sotto l'elio e il neon, in questo modo:

A questo punto, dovremmo riempire gli orbitali 3d... e invece no! L'elemento successivo all'argon, e cioè il potassio, ha le stesse proprietà chimiche del litio e del sodio; insomma, è un metallo alcalino. Ciò significa che è stato riempito l'orbitale 4s, prima del 3d! Invece, se si confrontano le precedenti strutture con quelle viste sopra degli elementi che hanno riempito gli orbitali 3p, si arguirà immediatamente che il gallio va posto sotto boro e alluminio, il germanio sotto carbonio e silicio, l'arsenico sotto azoto e fosforo, il selenio sotto ossigeno e zolfo, il bromo sotto fluoro e cloro, e il kripton sotto elio, neon e argon. E i dieci elementi ottenuti riempiendo gli orbitali 3d? Essi hanno proprietà diverse da quelle di tutti gli altri atomi visti finora, e quindi Bohr separò tra di loro i primi due gruppi dagli ultimi sei, inserendo in essi i metalli del blocco d:

Come si vede, in verde abbiamo indicato gli alcalini più l'idrogeno, che hanno un elettrone nell'orbitale s più esterno; in arancione gli alcalino-terrosi, con due elettroni nell'orbitale s più esterno, escluso l'elio; questi due gruppi formano il cosiddetto blocco s. In blu, in giallo (questi sono gli alogeni) e in azzurro (questi ultimi sono i gas nobili) vi sono gli elementi del blocco p, che hanno elettroni negli orbitali p più esterni. In fucsia infine abbiamo gli elementi del blocco d. Fu così che Bohr venne a disegnare una tavola periodica di forma invero insolita, ma il cui aspetto riflette alla perfezione il riempimento (in tedesco aufbau) degli atomi da parte degli elettroni. A questo punto appare chiaro che della Tavola Periodica di Bohr segue passo passo la configurazione elettronica degli atomi, e quindi è un ulteriore modo per guardare dentro gli atomi stessi!
Non preoccupatevi, non vi annoierò con tutte le configurazioni elettroniche di tutti gli elementi della tavola periodica: ormai avete capito il giochetto, e dovreste essere in grado di costruirvele da soli. Naturalmente, a patto di sapere quale orbitale verrà riempito dopo i 4p. L'ordine preciso è dato dalla cosiddetta Regola di Madelung, dal nome del suo scopritore Erwin Madelung (1881-1972): gli orbitali con un valore più basso di ( n + l ) vengono riempiti prima di orbitali con valori ( n + l ) maggiori. In altre parole, gli orbitali si riempiranno seguendo le frecce rosse diagonali di questa tabella:

La regola si fonda sul numero totale di nodi nell'orbitale atomico, numero che è dato da ( n + l ) e che è correlato all'energia dell'orbitale stesso. In caso di valori uguali di ( n + l ), l'orbitale con un valore di n minore viene riempito per primo. La regola ha alcune eccezioni, come ad esempio il palladio, ma si è dimostrata in ottimo accordo con l'esperienza. In base alla regola di Madelung, l'orbitale 4s (n + l = 4 + 0 = 4) viene occupato prima degli orbitali 3d (n + l = 3 + 2 = 5), esattamente come abbiamo visto sopra. Dopo i 4p, ad essere occupato per primo sarà il 5s, cui seguiranno i 4d, i 5p, il 6s, e solo a questo punto, quando Z avrà già toccato quota 56, verrà riempito il primo orbitale di tipo f, per la precisione il 4f. E così via.
Ogni riga della Tavola Periodica viene detta periodo, ed ogni colonna è chiamata gruppo (essi sono numerati con numeri romani da I ad VIII), composto da elementi con la stessa configurazione elettronica esterna, e quindi con le stesse proprietà chimiche. Ad esempio, nella famosa puntata della Serie Originale di "Star Trek" intitolata "Il mostro dell'oscurità" e nel film britannico "Island of Terror" (1966) sono descritti esseri la cui biologia è a base di silicio, non di carbonio (il suddetto film li chiama Siliconi, perchè silicio in inglese si dice "silicon"), ed anche biologi seri ammettono che la possibilità di una vita basata sul silicio è tutt'altro che ridicola, dato che i due elementi appartengono allo stesso gruppo, il quinto, ed hanno dunque le stesse proprietà chimiche!

Doodle dedicato da Google a Dmitrij Mendeleev
Bohr insomma collocò tutti gli atomi in cui si riempie un orbitale s sulla sinistra, in due colonne verticali (blocco s); gli elementi le cui strutture elettroniche riempiono orbitali di tipo p sono posti invece in sei colonne verticali sulla destra (blocco p); quelli che riempiono gli orbitali di tipo d sono posti in mezzo, in dieci colonne verticali (blocco d). Gli elementi del blocco d vengono chiamati anche metalli di transizione, e sono quasi tutti caratterizzati da lucentezza metallica, conducibilità elettrica e termica e paramagnetismo; di fatto, tutti questi elementi hanno configurazioni s e p praticamente identiche, perchè differiscono per gli elettroni che si trovano negli orbitali d ed f, particolarmente profondi. Tutti questi elementi sono dunque chimicamente molto simili, tanto che Mendeleev li aveva riuniti in un'unica colonna della sua vecchia tabella! Invece gli elementi che riempiono gli orbitali f sono disposti in due righe che andrebbero poste tra il blocco s e il blocco d, ma per evitare una tavola periodica di spropositata larghezza vengono collocate sotto la tabella. Quelli che riempiono l'orbitale 4f (la prima riga del blocco f) sono i cosiddetti lantanidi (in greco "nascosti") o terre rare, compresi fra il lantanio (Z = 56) e il lutezio (Z = 71). Nonostante il nome, essi non sono rarissimi nella crosta terrestre (ad eccezione del Promezio che non ha isotopi stabili), ma furono chiamati così perchè estratti da minerali all'epoca poco comuni: la prima delle terre rare ad essere isolata fu il cerio (Z = 58), scoperto nel 1803 in Svezia da Jöns Jacob Berzelius (1779-1848) e Wilhelm von Hisinger (1766-1852) ed in Germania, indipendentemente, da Martin Heinrich Klaproth (1743-1817). Gli elettroni dell'orbitale 4f sono schermati da quelli dell'orbitale 6s più esterni, per cui le loro righe risultano strettissime, ed essi sono particolarmente adatti per realizzare laser (il neodimio in particolare). Invece nella seconda riga del blocco f sono indicati i cosiddetti attinidi che riempiono l'orbitale 5f, compresi fra l'attinio (Z = 89) e il laurenzio (Z = 103), che riempiono gli orbitali 5f. Le loro proprietà chimiche sono analoghe a quelle dei lantanidi, ma la maggior parte di essi non esistono in natura (l'ultimo presente in natura è l'uranio con Z = 92), e sono stati prodotti artificialmente dall'uomo mediante reazioni nucleari o acceleratori di particelle. Gli elementi con Z > 100 sono noti anche come superpesanti, e sono fatti oggetto di una caccia serrata da parte dei chimici degli anni Duemila. L'elemento con Z più alto a noi noto è il cosiddetto oganessio (Z = 118), scoperto il 9 ottobre 2006 al Joint Institute for Nuclear Research di Dubna, in Russia, attraverso la collisione di atomi di californio e calcio, e così chiamato in onore del russo Jurij Colakovič Oganesian (1933-) che contribuì alla sua scoperta.
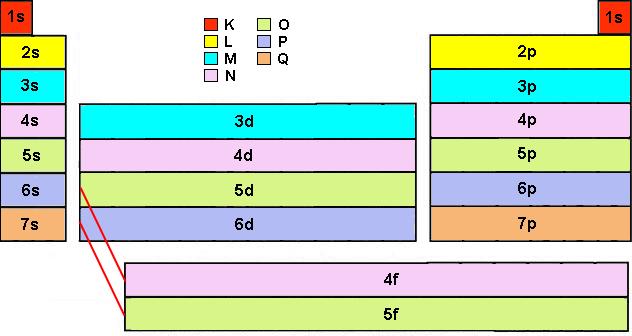
Le righe della tavola periodica NON rappresentano delle shell, o meglio questo vale solo per le prime due righe. Infatti, come mostra lo schema soprastante (in cui ogni colore individua una shell differente), per motivi energetici il blocco 3d si trova nella quarta riga della tabella e il blocco 4f addirittura andrebbe nella sesta riga. Le righe dunque non hanno significato fisico diverso dall'ordine di riempimento naturale della tavola stessa. Per curiosità, si consideri il palladio (con Z = 46), elemento scoperto nel 1803 dall'inglese William Hyde Wollaston (1766-1828) e battezzato con questo nome in onore dell'asteroide Pallade, scoperto due anni prima. Esso presenta l'orbita 4d chiusa, però uno di essi può saltare nell'orbita 5s, del tutto vuota, vista l'esigua differenza di energia tra questi orbitali. Ciò spiega perchè il palladio è chimicamente attivo, al punto da venire reso famoso nel 1989 dagli esperimenti sulla fusione fredda.
Ed ecco come appare oggi la tavola periodica, riorganizzata da Niels Bohr, con i blocchi indicati mediante colori omogenei (il blocco s in arancione, il blocco p in giallo, il blocco d in fucsia e il blocco f in azzurro). Si clicchi su di essa per vederne una versione più ampia.
Chiediamoci ora: la Tavola Periodica di Bohr ha una fine? In altre parole, vi è un ultimo elemento al di là del quale non si può procedere oltre? Ogni nucleo atomico esiste se la forza nucleare forte che tiene utili tra loro i nucleoni supera la repulsione coulombiana provocata dai protoni, tutti i di carica positiva. Ma la repulsione elettrostatica ha virtualmente raggio infinito, mentre la forza nucleare forte ha un raggio d'azione dell'ordine delle dimensioni di un protone, per cui riesce a legare solo neutroni tra di loro contigui. Ne consegue che, se il nucleo diventa troppo grosso, la repulsione tra le cariche positive dei protoni supera fatalmente la forza d'attrazione tra le cariche barioniche dei nucleoni (la carica barionica è l'entità in cui ha sede la forza nucleare forte, così come la carica elettrica è ciò in cui ha sede la forza elettromagnetica), e il nucleo diventa instabile; o, se preferite, radioattivo. L'ultimo elemento ad avere isotopi stabili è il piombo, con Z = 82; gli elementi successivi si trovano in natura solo perchè i loro isotopi hanno una vita media così lunga, da essere sopravvissuti fin dal tempo del Big Bang, come l'uranio (Z = 92), oppure fanno parte di catene di decadimento di questi ultimi: è il caso del radio, con Z = 88. Tali isotopi si dicono primordiali.
Al crescere del numero di nucleoni, i nuclei diventano sempre più instabili, e la loro emivita (cioè il tempo necessario affinché la metà esatta dei nuclei si disintegri) si accorcia sempre più. L'uranio-235 ha una emivita di 4,47 miliardi di anni; il plutonio-239 (Z = 94) di 24.000 anni; il californio-249 (Z = 98) di 351 anni; il fermio-257 (Z = 100) di 100 giorni; il nobelio-255 (Z = 102) di 3 minuti; il bohrio-274 (Z = 107) di 54 secondi; il darmstadtio-281 (Z = 110) di 11 secondi; il flerovio-288 (Z = 114) di 0,8 secondi; il livermorio-293 (Z = 116) di appena 61 millisecondi; e l'oganessio-294 (Z = 118) di soli 0,89 millisecondi! Appare evidente che, ad un certo punto, ulteriori isotopi avrebbero una vita media così corta, da disintegrarsi prima ancora di poter essere rilevati. Partendo da questa ipotesi, nel 1911 il chimico americano Elliot Quincy Adams (1888-1971) aveva previsto che non sarebbero potuti esistere elementi di massa atomica superiore a 256; come si è appena visto, la sua previsione si è rivelata troppo pessimistica, ma effettivamente i nuclei al di sopra di questa massa atomica hanno un'emivita così breve, che in chimica non possono avere alcuna utilità pratica. A sua volta Niels Bohr aveva previsto che non potrebbero esistere nuclei con numero atomico maggiore di 137, poiché il primo elettrone dell'orbitale 1s avrebbe dovuto viaggiare a velocità maggiore di quella della luce, ma la previsione ha poco senso perché il modello di Bohr, da noi discusso nel capitolo 3, è non relativistico, e non può essere applicato ad elementi i cui elettroni posseggono invece energie relativistiche. Usando invece l'equazione relativistica di Dirac, della quale discuteremo nel capitolo successivo, si ottiene che l'energia di legame supera il proprio limite superiore per la prima volta nei nuclei con 173 protoni: per gli elementi più pesanti, se l'orbitale più interno non è riempito, il campo elettrico del nucleo spinge un elettrone al di fuori dell'atomo, determinando l'emissione spontanea di un positrone, ma questo non succede se l'orbitale più interno è riempito. Dunque l'elemento 173 non rappresenta necessariamente le Colonne d'Ercole della tavola periodica.
In ogni caso, nonostante l'emivita così breve dei nuclei con massa atomica superiore a 256, alcuni chimici pensano che esistano delle "isole di stabilità" al di là di questo limite; in altre parole, configurazioni particolarmente stabili dei nucleoni nel nucleo farebbero sì che alcuni elementi esistano con vita media assai più lunga di quella attesa; sono questi i cosiddetti elementi superpesanti. Quest'ipotesi fu avanzata per la prima volta dal fisico americano Glenn Theodore Seaborg (1912-1999), lo scopritore del Plutonio, in onore del quale è stato battezzato il Seaborgio, l'elemento con Z = 106. Una prima isola di stabilità è attesa attorno a una massa atomica di 300 circa, e il già citato fisico russo Yuri Oganessian (1933-) sostiene che dovrebbe essercene una seconda intorno a Z = 164 (un valore davvero altissimo!), ma finora nessun isotopo di queste isole è stato scoperto. Nell'universo di Star Trek si postula che nel 2371 d.C. alla Federazione Unita dei Pianeti saranno noti 246 elementi e, come narrato nell'episodio "Post Mortem", l'equipaggio della "Voyager" scoprirà il 247-esimo nel suo viaggio di ritorno a casa, un isotopo con un nucleo formato da ben 550 nucleoni, e dunque davvero "obeso". Se la previsione sarà azzeccata, non ci resta che armarci di pazienza, ed attendere la scoperta di quegli elementi davvero superpesanti...
Vi sono anche delle versioni "esotiche" della tavola periodica. Eccone una "circolare", disegnata da Marco Piazzalunga:

.
Ed eccone addirittura una costruita sul modello della... Metropolitana di Londra, disegnata da Mark Lorch dell'Università di Hull nel Regno Unito (cliccate qui per vederne una versione a risoluzione maggiore):

.
Vediamo ora se è possibile eseguire l'esercizio contrario; cioè, preso un elemento qualsiasi della Tavola Periodica, ricostruire la sua configurazione elettronica utilizzando le regole sopra esposte. Scegliamo ad esempio l'argento, unanimemente considerato uno dei metalli più nobili e preziosi del pianeta. Nella crosta terrestre vi sono 0,08 grammi di argento per tonnellata, una quantità 20 volte superiore a quella dell'oro (0,004 grammi per tonnellata). L'argento si trova in natura sia allo stato nativo che in minerali come l'argentite (Ag2S) o l'argentopirite (AgFe2S3); grandi giacimenti d'argento si trovano in Canada, Australia, Stati Uniti, Messico e Perù; in Italia è presente nei giacimenti del Sarrabus in Sardegna. Noto fin dall'antichità (è già menzionato in testi cuneiformi del III millennio a.C.), il suo nome è collegato al greco αργός, "splendente". Le prime monete d'argento risalgono al VII secolo a.C., ed ancor oggi in francese "argent" è sinonimo di "denaro". Con questo metallo lucidato venivano realizzati gli specchi e le posate; ancor oggi i servizi di posate vengono chiamati "argenteria". Nel Perù precolombiano vi erano ricchissime miniere d'argento, poi sfruttate dagli spagnoli. L'argento dà il nome ad una nazione, l'Argentina, ed al suo principale fiume, il Rio de la Plata ("Fiume dell'Argento"). Le prime lastre fotografiche erano realizzate con bromuro d'argento, che ha la proprietà di essere fotosensibile, ed oggi alcune tra le migliori batterie in commercio sono del tipo argento-zinco e argento-cadmio; Il fulminato d'argento è usato come esplosivo, mentre lo ioduro d'argento è usato per inseminare le nubi e stimolare la provocare la pioggia. Alcuni composti, come il nitrato d'argento, possono essere nocivi per la salute umana. L'argento ha la più alta conducibilità elettrica tra tutti i metalli, superiore persino a quella del rame. Nel Buddhismo è il secondo dei sette tesori, e simboleggia la virtù. In molte cosmogonie, l'argento è associato alla luna e a divinità lunari. Secondo la tradizione, un licantropo poteva essere ucciso solo con proiettili d'argento, una lama d'argento o un bastone d'argento. Un tempo si credeva che il mercurio fosse una varietà liquida dell'argento, da cui il nome tradizionale di "argento vivo"; in latino si dice hydrargyrium ("argento liquido"), e da qui viene il suo simbolo chimico Hg. D'argento sono le posate e i candelabri che il vescovo Myriel regala a Jean Valjean nei "Miserabili" (1862) di Victor Hugo (1802-1885); il mitologico mithril, detto anche Argentovero o Argento di Moria, il metallo più prezioso lavorato dai Nani nell'universo partorito dalla fantasia di John Ronald Reuel Tolkien (1892-1973), era probabilmente una varietà di argento; e persino uno dei racconti del "Sistema Periodico" (1975) di Primo Levi (1919-1987) si incentra sull'argento.
 Costruiamo
dunque la configurazione elettronica dell'argento. Come si vede nella Tavola
Periodica di Bohr sopra riportata, esso si trova all'incrocio tra la quinta
riga dall'alto (Quinto Periodo) e l'undicesima colonna da sinistra (Gruppo I
B; si noti che i Gruppi del blocco p sono designati con lettera A,
quelli del blocco d con la lettera B). Siamo dunque nel blocco d. Onde
evitare di ricostruire tutta la configurazione degli orbitali a partire da 1s,
si parte dalla struttura del gas nobile precedente, che è il kripton,
e si scriverà [Kr] intendendo la sua intera configurazione, da noi
già costruita sopra. Seguendo la Regola di Madelung,
dopo l'orbitale 4p, l'ultimo riempito dal kripton, tocca agli orbitali 5s
e 4d. 5s è stato sicuramente riempito (dagli elementi Rubidio e
Stronzio), successivamente per arrivare all'argento occorre contare nove
metalli del blocco d, dunque nell'orbitale 4d dovremo sistemare altri nove
elettroni. La configurazione elettronica dell'argento si scriverà dunque [Kr]
5s2 4d9. Rappresentandola come abbiamo fatto per i
primi 36 elementi, avremmo un complicato schema come quello raffigurato qui a
sinistra. A questo punto, vi lancio una sfida. Provate voi lettori a scrivere
la configurazione elettronica completa del ferro
(Z = 26), quella del gadolinio (Z =
64) e quella del flerovio (Z = 114),
sicuramente più complicata; aiutatevi con la tavola periodica raffigurata qui
sopra. Troverete la soluzione in
fondo a questa pagina.
Costruiamo
dunque la configurazione elettronica dell'argento. Come si vede nella Tavola
Periodica di Bohr sopra riportata, esso si trova all'incrocio tra la quinta
riga dall'alto (Quinto Periodo) e l'undicesima colonna da sinistra (Gruppo I
B; si noti che i Gruppi del blocco p sono designati con lettera A,
quelli del blocco d con la lettera B). Siamo dunque nel blocco d. Onde
evitare di ricostruire tutta la configurazione degli orbitali a partire da 1s,
si parte dalla struttura del gas nobile precedente, che è il kripton,
e si scriverà [Kr] intendendo la sua intera configurazione, da noi
già costruita sopra. Seguendo la Regola di Madelung,
dopo l'orbitale 4p, l'ultimo riempito dal kripton, tocca agli orbitali 5s
e 4d. 5s è stato sicuramente riempito (dagli elementi Rubidio e
Stronzio), successivamente per arrivare all'argento occorre contare nove
metalli del blocco d, dunque nell'orbitale 4d dovremo sistemare altri nove
elettroni. La configurazione elettronica dell'argento si scriverà dunque [Kr]
5s2 4d9. Rappresentandola come abbiamo fatto per i
primi 36 elementi, avremmo un complicato schema come quello raffigurato qui a
sinistra. A questo punto, vi lancio una sfida. Provate voi lettori a scrivere
la configurazione elettronica completa del ferro
(Z = 26), quella del gadolinio (Z =
64) e quella del flerovio (Z = 114),
sicuramente più complicata; aiutatevi con la tavola periodica raffigurata qui
sopra. Troverete la soluzione in
fondo a questa pagina.
Dedichiamo alcune righe anche ai cosiddetti superatomi. Si tratta di gruppi di atomi (tra gli otto e i cento) incredibilmente di imitare il comportamento di altre sostanze. Per esempio, con tredici atomi di alluminio messi insieme in modo opportuno si riesce a simulare perfettamente il bromo, tanto che le due realtà sono indistinguibili dal punto di vista delle loro proprietà chimiche, nonostante il superatomo sia tredici volte più grande dell'atomo singolo! Anche il sodio è in grado di formare superatomi e imitare altri elementi, e ci sono validi motivi per ritenere che questa proprietà sia addirittura universale: tutti gli elementi pottebbero imitarne degli altri! Ma com'è possibile? Il fatto è che gli atomi si dispongono a formare un poliedro, e ognuno di loro si comporta come un protone o un neutrone del superatomo. Gli elettroni somo messi in comune e orbitano attorno a questa massa collettiva, formando uno stato della materia che è stato battezzato ironicamente "jellium" (da "jelly", "marmellata"). A seconda del tipo di poliedro, il superatomo avrà un numero maggiore o minore di elettroni da utilizzare nelle reazioni con altre sostanze. Se ne mette a disposizione sette, si comporta come il bromo o come un altro alogeno; se ne ha quattro, agisce come il silicio o un altro suo simile chimico, e così via.

Una foto eccezionale: un'auto britannica interamente decorata con la tavola di Mendeleev!
Per quanto strani, i superatomi perlomeno somigliano alla materia ordinaria, ma esistono altre stranezze chimico-fisiche legate alla tavola periodica, i cosiddetti punti quantici. Si tratta in un certo senso di "atomi virtuali", che seguono però le leggi della meccanica quantistica. Molti elementi possono formare i punti quantici, ma il più studiato e l'indio, parente stretto dell'alluminio, situato al confine tra metalli e semiconduttori. La costruzione di un punto quantico inizia realizzando una minuscola torretta, fatta di strati analoghi a quelli di una torta. Partendo dal fondo troviamo un semiconduttore, un isolante (di solito ceramica), l'indio, un altro strato di isolante più spesso e uno strato di metallo in cima. Al tutto si applica una corrente in grado di spostare elettroni dal basso in alto; questi dovrebbero fermarsi una volta giunti all'isolante, ma se lo strato è abbastanza sottile un elettrone riesce ad attraversarlo per effetto tunnel. Se a questo punto si interrompe la corrente, quell'elettrone rimane intrappolato nell'indio. Questo materiale gli lascia abbastanza spazio per passare tra un atomo e l'altro, e la particella va in giro libera senza farsi catturare. Se lo strato di indio è abbastanza sottile, i suoi atomi tutti insieme allora si comportano "magicamente" come un unico atomo, dotato di un elettrone in comune. Aggiungendo altri elettroni, essi si disporranno secondo il Principio di Pauli negli equivalenti di "superorbitali" e "superlivelli energetici". I punti quantici hanno forma appiattita (in inglese sono chiamati anche "pancake atoms", cioè "atomi frittella") e i loro livelli energetici sono diversi da quelli consueti. Di conseguenza, un'ipotetica tavola periodica costituita da auesti superatomi sarebbe più stretta di quella di Menedeleev, perché per loro non vale più la regola dell'ottetto; gli elettroni riempiono i livelli più velocemente e ci sono meno elementi tra un gas nobile e l'altro. I punti quantici più reattivi formano comunque legami tra di loro, ma non si comportano in modo analogo a nessun elemento naturale. E non si tratta di un semplice esercizio accademico, perché i punti quantici stanno mostrando un grande potenziale applicativo, soprattutto nei computer quantistici di nuova generazione, di cui parleremo nel capitolo seguente.
.
7.3 Il problema degli atomi multielettronici
Il problema di costruire le strutture atomiche degli atomi diversi dall'idrogeno è però molto più complicato di quanto si può credere. Se infatti abbandoniamo le strutture idrogenoidi, cioè con un solo elettrone, come gli ioni He+, Li2+, eccetera, non bisogna più tenere conto solo dell'interazione tra il nucleo e gli elettroni, ma anche l'interazione tra gli elettroni dell'atomo, ed è proprio questo che rende il problema insolubile dal punto di vista analitico. Prima di passare oltre, dunque, è bene spenderci su due parole. Se Z è il numero atomico di un atomo, vuol dire che il suo nucleo contiene Z elettroni, e quindi intorno ad esso ruotano Z elettroni. Nel modello quanto-ondulatorio di Schrödinger, la funzione d'onda deve dipendere dagli Z vettori posizione degli elettroni, e quindi da 3 Z coordinate numeriche. Se passiamo al modello di Dirac, del quale parleremo nel capitolo seguente, bisogna aggiungere pure gli spin, senza i quali la descrizione dell'aufbau atomico è incompleta. Bisogna aggiungere dunque una coordinata di spin per ogni elettrone, e di conseguenza già per l'elio le variabili necessarie sono otto. Se trascuriamo le interazioni spin-orbita e spin-spin, che in realtà non sono affatto trascurabili, bisognerà comunque tenere conto dell'interazione tra ogni elettrone e il nucleo, e tra ogni elettrone e i circostanti. Il problema diventa mostruosamente complicato già per atomi con pochi elettroni, figuriamoci se si arriva agli elementi superpesanti! Per salvare capra e cavoli, è possibile ricorrere ad un artificio matematico: supporre che gli elettroni siano isolati tra di loro. In tal modo ogni singolo elettrone potrebbe essere trattato come se appartenesse ad un atomo idrogenoide, e di conseguenza la funzione d'onda totale Ψ risulterà il prodotto delle Z funzioni d'onda di elettrone singolo. Infatti, sappiamo che la probabilità totale di eventi tra di loro indipendenti è il prodotto delle singole probabilità. Proprio partendo da questa ipotesi è possibile ricavare il Principio di Esclusione di Pauli, di cui si è parlato all'inizio di questo capitolo.
Non occorre essere scienziati per capire che tale semplificazione è eccessiva. Si può continuare a farla valere se facciamo l'ipotesi di campo medio, cioè se io considero la funzione d'onda come prodotto non delle singole funzioni d'onda idrogenoidi degli elettroni reali, ma delle funzioni d'onda di elettroni fittizi, che si muovono nel campo elettrico del nucleo e nel campo medio generato da tutti gli altri elettroni. In questo modo, gli elettroni degli atomi non idrogenoidi NON coincidono con quelli dell'atomo d'idrogeno. Intervengono in modo decisivo delle forze di scambio, che come vedremo caratterizzano anche lo studio delle molecole. Si suppone che in ogni punto dello spazio circostante il nucleo esista una distribuzione continua di carica elettrica, dovuta in realtà agli ( Z – 1 ) elettroni rimanenti quando si considera uno solo di essi, e di conseguenza è possibile scrivere Z equazioni di Schrödinger. Il sistema di equazioni integro-differenziali così ottenuto è pur sempre difficilissimo, e l'unica soluzione possibile è per via approssimata. La più brillante soluzione di questo dilemma è quella ottenuta alla fine degli anni venti del secolo scorso dal britannico Douglas Rayner Hartree (1897-1958) e dal russo Vladimir Aleksandrovic Fock (1898-1974): un metodo che parte dall'imporre una funzione d'onda di tentativo come soluzione delle suddette Z equazioni di Schrödinger: conviene ripescare l'ipotesi che tutti gli elettroni si trovino in uno degli stati idrogenoidi, cioè che non si "sentano" fra di loro, ed usare come soluzione di primo tentativo il loro prodotto. Essa viene sostituita nelle dette equazioni, e da esse si ricava una densità di carica di primo tentativo. Essa permette di calcolare una nuova energia potenziale, e di conseguenza di risolvere le equazioni di Schrödinger, ricavando una funzione d'onda che rappresenta la soluzione di ordine uno. Questa soluzione è diversa da quella di primo tentativo, ma rappresenta un'approssimazione migliore della soluzione esatta del nostro problema. Da essa si ricava una ulteriore approssimazione della densità di campo medio, e un'ulteriore approssimazione dell'energia potenziale. Risolvendo le nuove equazioni di Schrödinger ricaveremo un'approssimazione ancora migliore della funzione d'onda, che sarà la soluzione di ordine due.

Per farla breve, continuando di questo passo è possibile ottenere delle funzioni d'onda di ordine ( K + 1 ), che differiscono sempre di meno dalla funzione "vera" dell'ordine K precedente. Quello che Hartree e Fock hanno inventato è un vero e proprio algoritmo, cioè un procedimento analitico in cui introduco l'ordine K delle funzioni d'onda, ed esso mi restituisce l'approssimazione di ordine ( K + 1 ). Se, continuando a iterare lo stesso procedimento, non noto più apprezzabili differenze tra la funzione d'onda ψK e la successiva ψK+1, si dice che l'algoritmo converge, e quella che ho ottenuto è, a tutti gli effetti, la soluzione del mio problema, perchè tale funzione d'onda mi permette di trovare la densità di carica e il potenziale che compaiono nella medesima equazione di Schrödinger. Il campo elettrico caratterizzato da questa distribuzione di carica e da questo potenziale si dice campo medio autoconsistente. Questo procedimento è facilmente realizzabile con l'aiuto dei moderni, potenti calcolatori elettronici; si parla di metodo iterativo, poiché le stesse operazioni vengono eseguite molte volte di seguito, fino alla convergenza dei risultati. Da notare che quando Hartree applicò tale metodo per la prima volta, si accorse che la soluzione delle sue equazioni non convergeva, cioè il risultato continuava ad oscillare. Fu Fock a risolvere il problema, sostituendo a ψK una combinazione lineare di ψK e di ψK+1. Questo artificio sa un po' di ultima spiaggia, ma funzionò, perchè il raffronto tra le previsioni teoriche con esso realizzabili e i dati ottenuti sperimentalmente era più che soddisfacente. Per questo l'algoritmo da noi descritto è chiamato metodo di Hartree-Fock, e le soluzioni con esso ottenute forniscono una descrizione corretta dei livelli e degli orbitali solo se Z non è troppo alto. Per atomi molto pesanti, si ottengono risultati in accordo con l'esperienza solo utilizzando metodi statistici, come quello proposto da Enrico Fermi e dal fisico britannico Llewellyn Thomas (1903-1992), il cosiddetto metodo di Thomas-Fermi.
Quanto detto può essere utilizzato per studiare il più semplice degli atomi polielettronici, l'atomo di elio. L'equazione di Schrödinger corrispondente, che non starò a scrivere per semplicità, contiene necessariamente due termini di attrazione elettrone-nucleo (l'elio ha due elettroni) e un termine di repulsione tra i due elettroni. Questi termini sono tutti dello stesso ordine, dunque non possiamo trascurare l'uno rispetto all'altro. Ovviamente questa equazione non è risolubile in modo analitico, neppure con salti mortali degni dell'Uomo Ragno; bisogna allora ricorrere al metodo di Hartree-Fock. Come soluzione di primo tentativo all'ordine zero useremo gli orbitali atomici di atomo singolo dell'atomo di idrogeno:
ψ1 (r1) = 1s (r1) ; ψ2 (r2) = 1s (r2)
dove r1 e r2 indicano rispettivamente le posizioni del primo e del secondo elettrone. Iterando successivamente, si perviene a due soluzioni del tipo ψ1 (r1) e ψ2 (r2), per le quali l'algoritmo di Hartree-Fock converge. È allora possibile dire che la funzione d'onda dello stato fondamentale dell'atomo d'elio è:
ψ (r1, r2) = ψ1 (r1) ∙ ψ2 (r2)
Ma, anche nel semplice schema di elettroni indipendenti che avvertono il campo medio autoconsistente, non è possibile affermare che l'energia di ionizzazione dell'elio coincide con la somma E1 + E2 dei due autovalori dell'energia corrispondenti a ψ1 (r1) e ψ2 (r2), giacché tale somma deve comprendere anche l'energia di repulsione coulombiana tra i due elettroni. Risolvendo l'equazione si ricava per l'energia di ionizzazione l'espressione seguente:
![]()
dove R è la costante di Rydberg. Sostituendo ai simboli i valori numerici si trova Eionizz = – 74,6 eV, in buon accordo con il valore sperimentale di – 78,8 eV. Come si vede, chi rideva dei funambolismi di Hartree è costretto a ricredersi: il suo metodo funziona eccome. Qui sotto potete vedere una straordinaria immagine scattata da un team ispano-tedesco dell'Università di Heidelberg (l'immagine è tratta da questo sito); in essa si vede chiaramente proprio il movimento della coppia di elettroni in un atomo di elio. A 15,3 femtosecondi (fs, 1 fs =10–15 s) dall'inizio dell'esperimento, i due elettroni sono vicini al nucleo (centro dell'immagine), e quindi si allontanano da esso. Il colore indica la probabilità di trovare un elettrone lungo l'asse verticale e il secondo elettrone lungo l'asse orizzontale rispetto alla direzione di polarizzazione del laser usato per eccitare l'atomo. A 16,3 femtosecondi dall'inizio i due elettroni tornano di nuovo nella loro posizione iniziale; si muovono dunque con una pulsazione di circa un femtosecondo.

È però importante far notare che, nella discussione svolta finora, non sono mai stati chiamati in causa gli spin, che invece esistono ed interagiscono tra di loro, come vedremo nel capitolo seguente. Si sa che gli stati 1s hanno l = 0, perciò non sono in gioco momenti angolari orbitali: l'unico contributo al momento angolare è dato dallo spin medesimo. Ma come si compongono gli spin? Nei paragrafi 3.6 e 3.8 si è visto che:
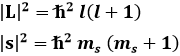
dove ms = 1 / 2. Evidentemente, nel nostro caso:
Ltot = L1 + L2 = 0
stot = ms1 + ms2 = 1
in unità h tagliata. Ora, si può dimostrare che:
| ms1 – ms2 | ≤ ms tot ≤ ms1 + ms2
Il momento angolare totale dell'elettrone, dovuto a un contributo orbitale e ad uno di spin, ma qui Ltot = 0; dunque, la legge di composizione degli spin coincide con quella dei momenti angolari totali. Poiché ms = 1 / 2, risulta:
0 ≤ ms ≤ 1
Ne consegue che, per l'elio, ms tot può valere o 0 o 1.
Se ms tot = 0, ne segue stot = 0. Ho una sola possibilità per la funzione d'onda, e perciò si parla di stato di singoletto.
Se invece stot = 1, ho tre possibilità:
stot = – 1 / 2 – 1 / 2 = – 1
stot = – 1 / 2 + 1 / 2 = 0
stot = + 1 / 2 + 1 / 2 = + 1
cioè stot può valere – 1, 0 o + 1. Ho tre possibilità per la funzione d'onda, per cui si parla di stato di tripletto.
Si può dimostrare che lo stato fondamentale dell'atomo di elio si trova nello stato di singoletto; lo stato di tripletto si ha solo negli stati eccitati. L'elio che si trova nello stato di singoletto prende il nome di paraelio, e le sue righe spettrali non presentano alcuna struttura fine, perchè stot = 0. L'elio che si trova nello stato di tripletto prende invece il nome di ortoelio, e mostra struttura fine. I due stati si distinguono bene fra di loro per via spettroscopica, e l'osservazione conferma la previsione teorica (ne dubitavate?)
Ma si può dimostrare anche che i due elettroni si schermano l'un l'altro la carica del nucleo; in altre parole, ciascuno dei due elettroni non sente la carica ( + 2 e ) del nucleo, ma essa viene parzialmente "cancellata" dalla carica negativa dell'altro elettrone, come se esso fosse una nube di carica distribuita attorno al nucleo. Questo fatto è generale: per esempio un elettrone della shell L del litio sente la carica nucleare ( + 3 e ) schermata dai due elettroni 1s sottostanti, e perciò si comporta anch'esso in parte come un elettrone idrogenoide, avvertendo solo una carica nucleare ( + e ). Quanto alle energie dei due stati di singoletto e di tripletto, ricavabili dall'equazione di Schrödinger, si scopre che l'energia dello stato di tripletto è sempre minore di quella dello stato di singoletto, e quindi, dove sia possibile realizzarlo, il tripletto è energeticamente favorito, ed è in questo stato che gli elettroni vanno a disporsi.
Il discorso sugli atomi polielettronici sarebbe lunghissimo e complicatissimo da affrontare, ma io mi fermo qui. Mio compito era quello di darvi un'idea su come si affrontano analiticamente questi problemi così complessi. Prima di passare oltre, però, una piccola curiosità. E se vi dicessi che esiste un inusuale stato atomico in cui l'elettrone non è né libero né legato a un nucleo? Nel 1968 il fisico teorico Walter Henneberger ipotizzò che fosse possibile ionizzare un atomo, per esempio con l'uso di un impulso laser, liberando un elettrone, senza però farlo allontanare troppo dal nucleo. Nonostante lo scetticismo di molti, fin dagli anni ottanta alcuni fisici sperimentali hanno cercato di realizzare questo strano sistema microfisico. A riuscire nell'impresa nel 2018 sono stati alcuni fisici dell'Università di Ginevra e del Max-Born-Institut für Nichtlineare Optik und Kurzzeitspektroskopie di Berlino. Il problema che gli scienziati hanno dovuto risolvere è complesso: occorre calibrare non solo l'intensità del laser (quanto più è intenso il fascio, tanto più facile è la ionizzazione) ma anche altri parametri, perché l'elettrone non deve sfuggire completamente, ma rimanere intrappolato nel campo elettrico sia del laser sia del nucleo. L'unico modo per ottenere questo risultato consiste nel trovare la forma corretta dell'impulso laser che produce l'effetto voluto. Al termine di una serie di calibrazioni, gli scienziati sono riusciti a liberare l'elettrone dal legame con il suo nucleo e a intrappolarlo nel campo elettrico del laser, come ipotizzato a suo tempo da Henneberger, grazie a una scoperta sorprendente. Contrariamente a quanto ci si potrebbe aspettare, infatti, esiste un valore limite dell'intensità del laser, in corrispondenza del quale non è più possibile ionizzare l'atomo, ma oltre il quale si può riprendere il controllo dell'elettrone: nel mezzo c'è quella che i fisici hanno chiamato la "Valle della Morte". Applicando un fascio di 100.000 miliardi di Watt per centimetro quadrato, circa 1000 miliardi di volte l'intensità della radiazione solare sulla superficie terrestre, è stato possibile andare oltre la "Valle della Morte": un risultato davvero incredibile, che conferma una delle previsioni della Meccanica Quantistica.

In
questa foto eccezionale vedete l'ideogramma giapponese
che significa "atomo" tracciato utilizzando atomi di ferro!
(da
questo sito)
.
7.4 Dagli atomi alle molecole
È evidente che lo studio degli atomi isolati è insufficiente per comprendere la struttura della materia. Infatti gli atomi si organizzano per dar vita ai diversi stati di aggregazione, e il mattone base di questi stati è la molecola. Con questo nome, che significa "piccola massa", si indica la più piccola porzione di materia che ne conserva tutte le proprietà fisiche e chimiche. In pratica si tratta di un aggregato di atomi collegati da quello che viene chiamato legame chimico. In passato si riteneva che tale legame fosse dovuto a una forza chiamata "forza molecolare", la cui natura era sconosciuta. Dopo la scoperta dell'elettrone e del nucleo, fu chiaro invece che questa forza rappresentava un sottocaso dell'interazione elettromagnetica. Studiare però in modo rigoroso attraverso l'equazione di Schrödinger come vadano le cose è però particolarmente difficile, per l'elevato numero di particelle e di gradi di libertà in gioco. Se una molecola è costituita da tre atomi, ciascuna con un nucleo e 30 elettroni, ho 99 gradi di libertà totali nelle tre direzioni dello spazio. Per descrivere il "sistema molecola" occorre insomma una funzione d'onda che contiene tutte le coordinate delle particelle, misurate rispetto al centro di massa della molecola; e per riuscirci occorrono particolari artifici e semplificazioni.
Una di queste consiste nel partire dallo studio della molecola più semplice possibile, la cosiddetta molecola ione-idrogeno H2+. Essa è costituita da due nuclei d'idrogeno con un solo elettrone; praticamente si tratta della molecola d'idrogeno H2 cui è stato strappato un elettrone. La corrispondente equazione di Schrödinger è complicatissima da risolvere alle quadrature, cioè per via analitica, perchè gli elettroni si muovono attratti dai nuclei, ma anche i nuclei si muovono nel campo elettrico generato dagli elettroni, e per di più i nuclei si attraggono fra di loro. Per semplificare le cose si introducono due approssimazioni. La prima è la cosiddetta approssimazione adiabatica, ideata da Max Born e da Julius Robert Oppenheimer (1904-1967), il famoso capo del progetto Manhattan, che consiste nel trascurare il potenziale dei nuclei, cioè nel ritenere i nuclei fermi rispetto agli elettroni. La seconda approssimazione consiste nell'utilizzare il metodo della combinazione lineare degli orbitali atomici (LCAO, "linear cobination of atomic orbitals"), cioè considerare una funzione d'onda risultante dalla combinazione lineare delle funzioni d'onda degli orbitali atomici. Per semplicità, detti a e b i nuclei della molecola ione-idrogeno, chiameremo 1sa la funzione d'onda dell'elettrone che orbita intorno al nucleo a nell'orbitale 1s, e 1sb la funzione d'onda di quello che orbita intorno al nucleo b nell'orbitale 1s. Detti ca e cb due parametri opportuni, la funzione d'onda cercata sarà:
ψ = ca ∙ 1sa + cb ∙ 1sb
Sostituendo tale funzione d'onda nell'equazione di Schrödinger della molecola ione-idrogeno ed operando gli opportuni calcoli, è possibile trovare due soluzioni, una con ca+ = cb+ e una con ca– = – cb–. Imponendo la normalizzazione delle funzioni d'onda (l'integrale del loro modulo quadrato è pari ad uno), si ottengono due risultati, ψ+ e ψ–, così esprimibili:
dove s è chiamato integrale di sovrapposizione. Per chi maneggia gli strumenti dell'Analisi Matematica, esso ha questa espressione analitica:
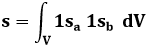
Questo è l'integrale su tutto il volume del prodotto delle due funzioni d'onda, dunque è nullo là dove lo è una delle due funzioni, mentre vale uno se si ha 1sa ≈ 1sb, cioè se i due nuclei si avvicinano moltissimo tra di loro; in pratica, s è tanto maggiore quanto minore è la distanza tra i due nuclei, cioè quanto più i due orbitali si sovrappongono: da qui il nome di "integrale di sovrapposizione". Nel caso della molecola ione-idrogeno, s assume questa forma analitica:
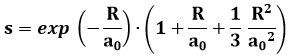
dove R è la distanza dal nucleo, ed a0 è il raggio della prima orbita di Bohr. La sua rappresentazione analitica è la seguente:

Come si vede, per R > 3 a0, l'integrale di sovrapposizione ha un valore pressoché trascurabile. In altre parole, se i due nuclei si allontanano più di 3 a0 l'uno dall'altro, cioè di circa 1,6 Ångstrom, si può ritenere che la sovrapposizione di 1sa ed 1sb sia trascurabile, per quanto in linea di principio non sia mai nulla. Si introduce anche il cosiddetto integrale di scambio:

Non è facile attribuirgli un significato fisico: essendo presenti nell'integrale due stati diversi, non posso interpretarlo come la forza repulsiva elettrostatica, perchè non so in quale dei due stati si trova l'elettrone. Si preferisce interpretare k come legato alla frequenza con cui i due stati si scambiano l'elettrone. Si tratta in effetti di un oggetto del tutto privo di corrispondente classico, un mero effetto quantistico non rintracciabile nell'ipotesi quantomeccanica. Mediante calcoli molto complicati è possibile risalire alla sua forma analitica:
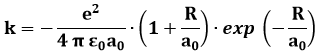
Quanto all'energia dei due stati quantistici ψ+ e ψ– dell'elettrone nella molecola ione-idrogeno, introducendo un ulteriore termine J che esprime l'interazione dell'elettrone con il nucleo b quando forma un legame con il nucleo a, i due stati energetici valgono:
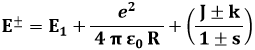
In tale formula:
E1 è l'energia dell'elettrone nella prima orbita di Bohr, coincidente con il valore trovato nel modello quantomeccanico, e quindi è l'energia che l'elettrone possiede se forma un atomo con uno solo dei due nuclei, come se l'altro fosse a distanza infinita;
il secondo termine ( e2 / 4 π ε0 R ) è l'energia di repulsione tra i due nuclei;
il terzo termine ( J ± k )/( 1 ± s ) è un termine il cui significato non è immediatamente intuibile, che tiene conto dello scambio dell'elettrone da un nucleo all'altro e della sovrapposizione tra le funzioni d'onda dei due atomi singoli. Esso insomma è il termine di interazione, il vero responsabile della coesione molecolare.
Se rappresentiamo le due energie E+ ed E– in funzione della distanza R tra i due nuclei, si ottiene il diagramma sottostante, tracciato a mano libera dall'autore di questo sito:
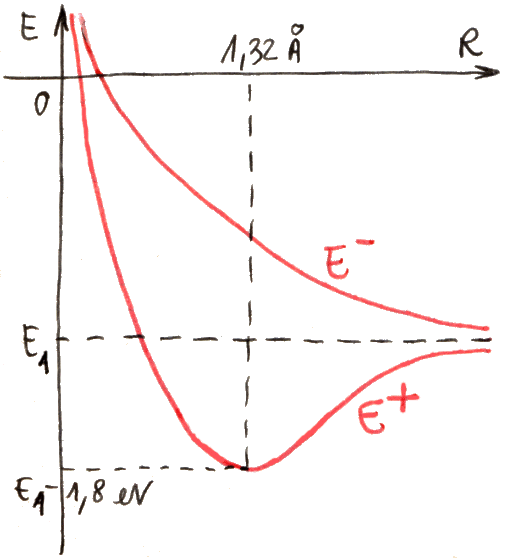
Come si vede, per R → ∞ essi tendono entrambi ad E1, cioè al valore dell'energia dell'elettrone legato ad un solo nucleo, com'è sensato aspettarsi. Mentre però E– è sempre decrescente, E+ presenta un minimo, e dunque rappresenta una buca di potenziale. Il minimo si trova ad R = 1,32 Å, e vale EMIN = E1 – 1,8 eV = – 15,39 eV. A piccole distanze dai nuclei, entrambe le energie risultano infinite, per via della repulsione coulombiana. A grandi distanze dei nuclei, invece, l'elettrone forma un legame con uno solo di essi, mentre l'altro nucleo resta isolato. A distanze intermedie, presentando E+ un minimo, esisteranno degli stati legati; infatti in quella situazione l'energia della molecola ione-idrogeno è minore dell'energia della molecola dissociata. Insomma, se la molecola si trova in uno stato la cui energia è compresa fra EMIN ed E1, per portarla alla dissociazione occorre fornirle energia. È chiaro che alla dissociazione la molecola non può arrivare da sola, senza qualcuno che le fornisca energia dall'esterno; pertanto, E+ è l'energia posseduta da una molecola stabile di H2+. Invece, E– > E1 per qualunque valore di R; dunque, se la molecola possiede energia E–, si parla di stato non legato. La funzione d'onda ψ+, associata all'energia E+, rappresenta quello che viene chiamato un orbitale legante, mentre la ψ– rappresenta un orbitale antilegante. In altre parole, una molecola descritta dalla funzione d'onda ψ– è instabile per natura, e non si forma; essa è stabile solo se il comportamento elettronico è descritto dalla funzione d'onda ψ+. Effettivamente, l'andamento dell'energia dell'elettrone nella molecola di H2+ ottenuto sperimentalmente ricalca proprio l'energia della funzione d'onda ψ+; il suo minimo si trova in corrispondenza di R = 1,06 Å e giunge a 2,648 eV al di sotto di E1, in buon accordo con le previsioni teoriche del modello di Bohr-Oppenheimer, pur inficiato da tante approssimazioni.
Ora, la forma analitica della funzione d'onda dell'orbitale 1s dell'atomo di idrogeno secondo la Meccanica Quantistica è:
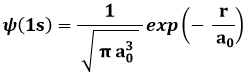
Si tratta, come si vede, di un esponenziale decrescente (più precisamente, è la sola parte radiale dell'orbitale in questione). Per ottenere ψ+ occorre sommare queste espressioni nella (7.1), per ottenere ψ– occorre sottrarle. Il risultato è rappresentato nei seguenti disegni a mano libera:
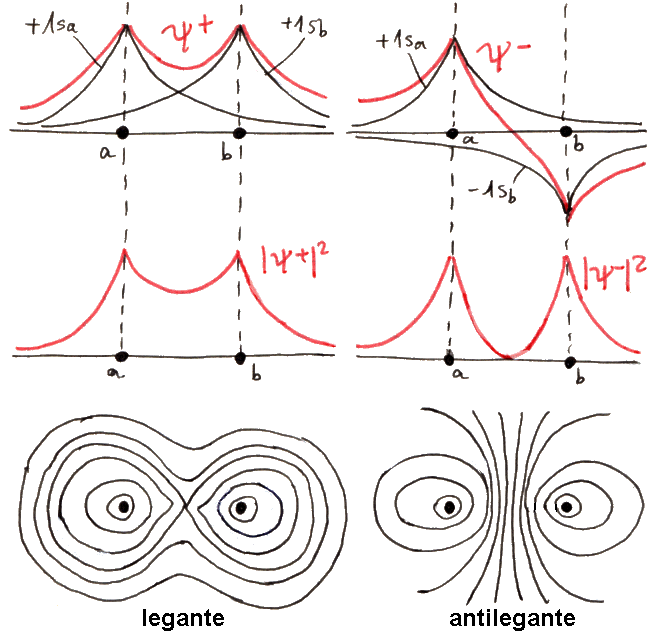
Sopra si vedono gli andamenti di ψ+ e di ψ–, sotto i corrispondenti andamenti di |ψ|2. Come si osserva, il modulo quadrato |ψ+|2 è grande tra i due nuclei, dove c'è un'elevata probabilità di trovare l'elettrone,mentre |ψ–|2 si annulla proprio nel bel mezzo dell'ipotetica molecola. Insomma, sul piano normale alla congiungente i due nuclei nel suo punto medio, detto piano assiale, non c'è alcuna probabilità di trovare l'elettrone. Ora, se l'elettrone si trova tra i due nuclei, scherma le loro cariche, impedendo che si respingano, e attraendoli entrambi a sé contribuisce alla coesione molecolare. Ma se i due nuclei sono affacciati l'uno all'altro con le loro cariche positive, è naturale che la molecola si dissoci. Se rappresentiamo le linee di ugual probabilità di trovare l'elettrone, come le isoipse di una carta geografica, che congiungono punti di ugual altitudine, la cosa diventa ancora più chiara, come si vede nella figura soprastante.
Quelli così illustrati prendono il nome di orbitali molecolari: una sola nube di probabilità di trovare l'elettrone circonda entrambi i nuclei! Per indicarli si usa la lettera greca σ (sigma), equivalente greco della s di 1s, e per ricordare che provengono dall'orbitale atomico 1s si scriverà σ(1s) e σ*(1s); gli orbitali antileganti infatti vanno indicati con un asterisco. σ(1s) insomma corrisponde a ψ+, σ*(1s) a ψ–. Usando una nomenclatura tedesca, σ(1s) si dice orbitale gerade ("pari"), σ*(1s) si dice orbitale ungerade ("dispari"), perchè, come si verifica subito, l'orbitale legante è pari, quello antilegante è dispari rispetto all'inversione delle coordinate spaziali. Le rispettive funzioni d'onda dunque sono pari a:
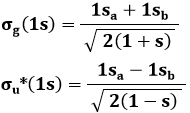
Se i due nuclei sono molto lontani, cioè se R → ∞, si ha s → 0 e le precedenti divengono:
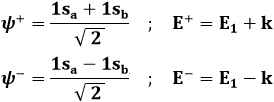
Si può dimostrare che le cose nella molecola ione-idrogeno vanno come se l'elettrone, descritto inizialmente dallo stato 1sa intorno al nucleo a, si trasferisse nello stato 1sb intorno al nucleo b, per poi tornare ad oscillare in 1sa intorno ad a, e così via. La frequenza con cui tale scambio avviene si può stimare pari a:
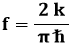
 Dunque l'integrale di scambio
è una stima della frequenza con cui i due nuclei di H2+
si scambiano l'elettrone. Si dice anche che l'elettrone
risuona tra gli stati 1sa
e 1sb. Anche se vi sembrerà strano, questo stato di cose
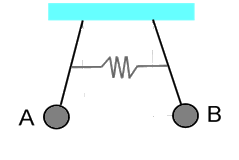
ricorda da vicino un sistema macroscopico detto
oscillatore armonico doppio e costituito da
due pendoli semplici con masse uguali e collegati da una molla, detti
A e B, come mostra lo schema qui a fianco. Mettiamo in oscillazione
uno di essi, ad esempio quello di sinistra. Il comportamento dell'oscillatore
armonico può essere simulato dalla
applet contenuta in questo sito, che vi invito a provare. Studiando
l'equazione del moto dei due oscillatoi armonici si scopre che prima oscilla uno
dei pendoli mentre l'altro è pressoché fermo, quindi l'energia si trasferisce al
secondo pendolo e quest'ultimo oscilla come oscillava il primo, ma in
opposizione di fase, mentre il primo si ferma o quasi; poi l'oscillazione viene
di nuovo comunicata al primo pendolo, e così via, in un continuo passaggio
periodico di energia dall'uno all'altro. Dette ω+ e ω–
due pulsazioni opportune e dette w+
e w– due opportune costanti, si
scopre che le equazioni del moto dei due pendoli sono date da:
Dunque l'integrale di scambio
è una stima della frequenza con cui i due nuclei di H2+
si scambiano l'elettrone. Si dice anche che l'elettrone
risuona tra gli stati 1sa
e 1sb. Anche se vi sembrerà strano, questo stato di cose
ricorda da vicino un sistema macroscopico detto
oscillatore armonico doppio e costituito da
due pendoli semplici con masse uguali e collegati da una molla, detti
A e B, come mostra lo schema qui a fianco. Mettiamo in oscillazione
uno di essi, ad esempio quello di sinistra. Il comportamento dell'oscillatore
armonico può essere simulato dalla
applet contenuta in questo sito, che vi invito a provare. Studiando
l'equazione del moto dei due oscillatoi armonici si scopre che prima oscilla uno
dei pendoli mentre l'altro è pressoché fermo, quindi l'energia si trasferisce al
secondo pendolo e quest'ultimo oscilla come oscillava il primo, ma in
opposizione di fase, mentre il primo si ferma o quasi; poi l'oscillazione viene
di nuovo comunicata al primo pendolo, e così via, in un continuo passaggio
periodico di energia dall'uno all'altro. Dette ω+ e ω–
due pulsazioni opportune e dette w+
e w– due opportune costanti, si
scopre che le equazioni del moto dei due pendoli sono date da:
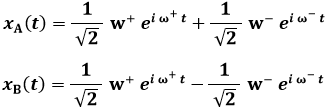
dove l'esponenziale immaginario equivale ad un'oscillazione armonica. I due esponenziali immaginari si dicono modi normali di vibrazione, e si scopre che tute le oscillazioni del sistema sono combinazioni lineari di questi due modi normali, esattamente come tutte le funzioni d'onda della molecola ione-idrogeno sono combinazioni lineari opportune delle funzioni d'onda 1sa e 1sb! L'elettrone si trova a ruotare periodicamente intorno ad uno solo dei due nuclei, poi intorno all'altro, poi di nuovo intorno al primo, e così via ad intervalli regolari. I sistemi dinamici simili all'oscillatore armonico doppio e alla molecola ione-idrogeno vengono chiamati sistemi bistabili, perchè oscillano in continuazione tra due situazioni stabili senza poter decidere quale delle due li rappresenta perfettamente. L'arte è piena di raffigurazioni di questi sistemi ambigui, in cui lo sguardo continua ad oscillare tra due diverse immagini senza potersi soffermare su nessuna di esse, come mostrano i cinque esempi sottostanti:

Considerando il primo disegno in alto a sinistra, si possono riconoscere in esso sia una donna giovane che una anziana; l'occhio umano non sa decidere se quella che vede è l'una o l'altra, e continua ad oscillare tra la vecchia e la giovane, tanto che l'occhio della prima si trasforma continuamente nell'orecchio della seconda, mentre il cervello riconosce ora l'uno ora l'altro. In realtà quel particolare rappresenta entrambe le cose, e la probabilità che noi riconosciamo l'occhio è identica alla probabilità che noi riconosciamo l'orecchio. Si tratta di "sistemi indecidibili, e per questo si parla anche di indecisione oscillante.
Lo stesso fenomeno è rintracciabile nella letteratura italiana, dove esiste una figura retorica chiamata anfibologia (dal greco amphibolìa, "ambiguità"), ad indicare una frase con significati ambigui ed interpretabili in più modi. Ecco un esempio elaborato dalla linguista italiana Bice Mortara Garavelli (1931-): « Una vecchia porta la sbarra ». Che significato ha questa frase? Un'anziana signora trasporta una sbarra di metallo, oppure una casa sbarrata da un antico portone? Qui l'anfibologia deriva dal duplice significato di "vecchia" (sostantivo o aggettivo), "porta" (verbo o sostantivo) e "sbarra" (sostantivo o verbo). Un altro esempio, stavolta elaborato da Mauro Aresu: « Ho visto mangiare i gatti ». Ho osservato qualcuno che si sfamava con i poveri felini, oppure i medesimi felini che divoravano delle crocchette? E c'è anche una celebre anfibologia dantesca:
 « Giunse quel
mal voler che pur mal chiede
« Giunse quel
mal voler che pur mal chiede
con lo 'ntelletto, e mosse il fummo e 'l vento
per la virtù che sua natura diede. » (Purg. V, 112-114)
Esistono due interpretazioni diverse di questo brano. Nell'una, "quel mal voler" è il soggetto ed è il diavolo; "giunse", cioè "arrivò", e "mosse il fumo e il vento", mentre "che pur mal chiede con lo 'ntelletto" (cioè che desidera solo il male con la sua intelligenza) è un attributo del diavolo. Ma si può leggere anche in un altro modo: "quel mal voler che pur mal chiede" (cioè quella cattiva volontà che cerca solo il male) è il complemento oggetto, il soggetto è sottinteso e il predicato "giunse" non vuol dire "arrivò", ma "congiunse", "unì": "egli unì la sua cattiva volontà che cerca solo il male con le capacità della sua intelligenza", e di conseguenza "mosse il fumo e 'l vento." Quale delle due è l'esatta interpretazione? In verità, la mente continua ad oscillare tra le due con regolarità, senza riuscire a decidersi, con un procedimento di indecisione molto simile a quella che governa la molecola ione-idrogeno!
.
7.5 Il legame covalente
Il metodo descritto in quel che precede per affrontare il problema degli atomi polielettronici e quello della molecola ione-idrogeno è lo stesso con cui si prende il toro per le corna nel caso di molecole polielettroniche. Questo è il caso della molecola d'idrogeno (H2). Si parte dal modello ad elettroni singoli, cioè si ritiene che la funzione d'onda che descrive il moto degli elettroni dentro la molecola sia una combinazione lineare di funzioni d'onda idrogenoidi. Siccome qui abbiamo due elettroni, per distinguere le loro funzioni d'onda si è soliti chiamare:
1sa(1) la funzione d'onda del primo elettrone che ruota solo intorno al nucleo a;
1sb(1) la funzione d'onda del primo elettrone che ruota solo intorno al nucleo b;
1sa(2) la funzione d'onda del secondo elettrone che ruota solo intorno al nucleo a;
1sa(1) la funzione d'onda del secondo elettrone che ruota solo intorno al nucleo b.
Queste funzioni sono ormai perfettamente conosciute. La funzione di primo tentativo sarà allora del tipo:
ψ = [ 1sa(1) ± 1sb(2) ] ∙ [ 1sa(2) ± 1sb(1) ] (7.2)
Ripetendo calcoli analoghi a quelli del paragrafo precedente, si trova il risultato illustrato qui sotto. Come si vede, l'energia in funzione della distanza R fra i due nuclei ha un andamento molto simile a quello della molecola ione-idrogeno; qui il minimo si trova in corrispondenza di R = 0,85 Å ed è situato 2,65 eV sotto l'energia di molecola indissociata (quella cui corrisponde R → ∞). Ora, i risultati sperimentali ci dicono che la distanza di equilibrio dei due nuclei nella molecola di idrogeno è di 0,74 Å, in buon accordo con la teoria; ma l'energia di dissociazione della molecola, cioè il dislivello tra fondo della buca e bordo per R → ∞, è in realtà pari a 4,75 eV. Questo modello dunque prevede bene la struttura della molecola, ma non le sue caratteristiche spettroscopiche. Perchè?
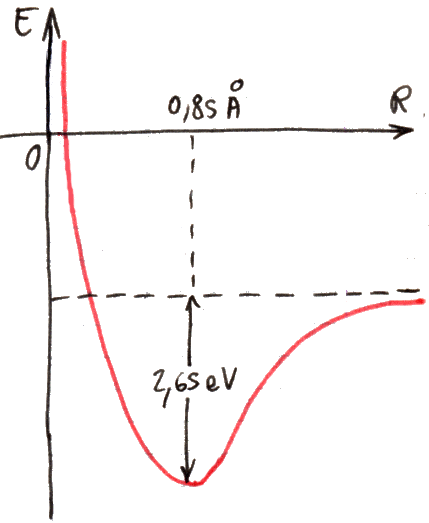
La risposta è semplice: qui non abbiamo più un solo elettrone, ne abbiamo due. Dunque, oltre all'attrazione tra nucleo ed elettrone, di cui si è tenuto conto, qui esiste anche la repulsione fra i due elettroni, di cui nella funzione di primo tentativo (7.2) non vi è traccia, avendo usato funzioni d'onda di elettrone singolo. Tuttavia, la (7.2) può fornirci alcune preziose informazioni circa il comportamento degli elettroni nell'atomo d'idrogeno. Infatti, se sviluppo la somma dei prodotti, ho:
ψ = 1sa(1) 1sa(2) ± 1sa(1) 1sb(2) ± 1sb(1) 1sa(2) + 1sb(1) 1sb(2) (7.3)
Dunque, ψ si può vedere come combinazione lineare, con coefficienti opportuni, di due diverse funzioni d'onda:
ψi = 1sa(1) 1sa(2) + 1sb(1) 1sb(2)
ψc = 1sa(1) 1sb(2) + 1sb(1) 1sa(2)
Si osserva subito che ψi è la somma di prodotti di funzioni d'onda idrogenoidi relative ad elettroni diversi, ma riferite allo stesso nucleo: 1sa(1) 1sa(2) descrive la situazione in cui entrambi gli elettroni ruotano intorno al nucleo a, e nessuno intorno al nucleo b; 1sb(1) 1sb(2) descrive invece la situazione in cui i due elettroni sono entrambi proprietà del nucleo b, mentre a resta a bocca asciutta. Questo significa che, in entrambi i casi, uno dei due atomi ha un elettrone in più, e l'altro un elettrone in meno. La molecola in pratica è formata da due ioni: uno ione positivo (H+), detto catione, ed uno ione negativo (H–), detto anione, tenuti insieme dalla reciproca attrazione. Dunque, ψi descrive quello che si chiama legame ionico tra due atomi: uno dei due strappa l'elettrone all'altro, entrambi diventano ioni di segno contrario, e la reciproca attrazione dà vita al legame atomico. Siccome a può strappare l'elettrone a b con la stessa facilità con cui b lo può strappare ad a, è evidente che la configurazione H+H– è statisticamente equivalente a H–H+, e perciò nella ψi si ha che 1sa(1) 1sa(2) e 1sb(1) 1sb(2) sono presenti con pesi uguali. Tale legame fu studiato approfonditamente dal già citato Erwin Madelung (1881-1972).
Quanto a ψc, essa è una combinazione lineare di 1sa(1) 1sb(2) e 1sb(1) 1sa(2), termini in cui un elettrone è legato solo ad un atomo, uno all'altro. Allora i due elettroni sono condivisi dai due nuclei. In questo caso, esattamente come nella molecola ione-idrogeno, il legame è assicurato dalla formazione di un orbitale legante. In questo caso si parla di legame covalente, che fu descritto per la prima volta dal chimico statunitense Gilbert Lewis (1875-1946). Legame ionico e legame covalente sono due modi del tutto diversi di formare un legame chimico, entrambi rappresentati nella (7.3). Non allo stesso modo, però. e basta un piccolo calcolo per rendersene conto. Infatti, l'energia necessaria per strappare l'elettrone a un atomo di idrogeno, detta energia di ionizzazione, vale ben 13,6 eV, pari all'energia tra il primo livello di Bohr e quello all'infinito:
Ha + 13,6 eV → Ha+ + 1 e–
Invece, se l'elettrone è catturato da un atomo d'idrogeno per dar vita a uno ione H–, l'energia liberata è pari solo a 0,715 eV, detta affinità elettronica:
Hb + 1 e– → Hb– + 0,715 eV
Dunque, per creare una coppia Ha+ – Hb–, occorrono 13,6 – 0,715 ≈ 12,9 eV. Ciò può essere suscettibile di un'interessante rappresentazione grafica. Associamo al livello di energia dei due atomi separati, Ha e Hb, un valore pari a zero. Per portarli allo stato ionizzato (Ha+ e Hb–) devo fornire loro 12,9 eV. Ma questi ioni sono, a priori, a distanza infinita; per riunirli in una molecola devo avvicinarli. Sappiamo già che il potenziale presenta una buca; però, come si vede dalla figura sottostante, il minimo della curva sta sempre al di sopra del livello di energia nulla. Naturalmente, avvicinando ulteriormente i nuclei, questi tendono a respingersi, e l'energia cresce. Questo fatto ci dice che il carattere della molecola di idrogeno è quasi esclusivamente covalente.
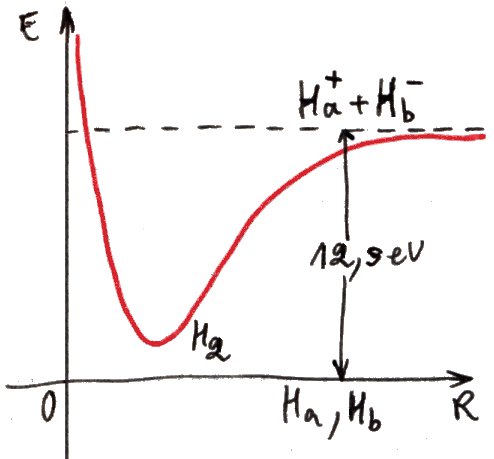
Diverso è il discorso per le molecole eteronucleari, cioè composti da atomi diversi. Consideriamo ad esempio il cloruro di sodio, che compone il comune sale da cucina. Si è visto che il sodio fa parte del gruppo 1 della tavola periodica, i cosiddetti alcalini, cioè ha un solo elettrone nella shell s più esterna. Per "chiudere la shell" e minimizzare la propria energia, esso tende a perdere quell'elettrone, trasformandosi in un ione Na+. Al contrario, il cloro fa parte del gruppo 8, i cosiddetti alogeni, cui manca esattamente un elettrone per completare la sua struttura elettronica più esterna. Dunque tende a conquistarlo, strappandolo a qualcuno. Si dice che il sodio ha un comportamento elettropositivo, il cloro un comportamento elettronegativo. Per ionizzarsi, il sodio richiede 5,14 eV; ma se l'elettrone perso è acquistato dal cloro, questo restituisce 3,72 eV! In altre parole:
Na + 5,14 eV → Na+ + 1 e–
Cl + 1 e– → Cl– + 3,72 eV
Sommando le precedenti membro a membro, si ha:
Na + Cl + 1,42 eV → Na+ + Cl–
Stavolta il dislivello tra gli atomi neutri isolati e gli ioni corrispondenti a distanza infinita è di soli 1,42 eV. Dunque, quando avviciniamo gli ioni per formare la molecola, il minimo del potenziale ha energia inferiore al livello zero di atomi isolati!
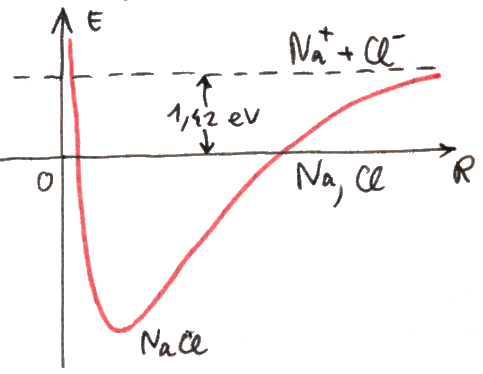
Dunque, lo stato di legame ionico per sodio e cloro è una configurazione energeticamente conveniente: per separare i due atomi legati da un legame ionico io devo fornire loro energia, mentre nel caso dell'idrogeno gli ioni H+ e H– tendono spontaneamente a perdere l'energia residua e a tornare nello stato di atomi neutri singoli. Infatti, nel cloruro di sodio il legame è del tutto ionico. "O quasi", dovremmo aggiungere, avendo imparato che in Meccanica Quantistica lo stato di un sistema è sempre la combinazione lineare di stati differenti; comunque, nella molecola d'idrogeno la percentuale di legame ionico, cioè il modulo quadrato del coefficiente con cui ψi entra nella (7.3), è bassissima, così come nella molecola di NaCl è bassissima la percentuale di legame covalente (in questo caso non si può neppure parlare di "molecola ionica", ma di "cristallo ionico".
I due casi che abbiamo esaminato sono casi estremi di perfetto legame covalente (due atomi uguali) e di perfetto legame ionico (due atomi quasi complementari, uno con un solo elettrone esterno e uno cui manca un solo elettrone esterno). In realtà, nella maggioranza dei casi le molecole sono casi intermedi fra quei due estremi, in cui la funzione d'onda complessiva ψ è una combinazione lineare di una parte ionica e di una covalente con pesi comparabili, esattamente come gli uomini con capelli del tutto neri e quelli con capelli del tutto biondi sono una minoranza rispetto a tutti coloro i cui capelli hanno una delle possibili sfumature intermedie di castano tra di essi.
Tornando ora alla molecola d'idrogeno H2, nella (7.3) il coefficiente della ψi è trascurabile, e quindi possiamo utilizzare la sola ψc, opportunamente normalizzata:
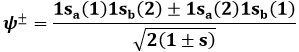
s è l'integrale di sovrapposizione introdotto nel paragrafo precedente. Qui ho due elettroni, esattamente come nell'atomo di elio, dunque posso ripetere tutto il discorso svolto in quel caso sia rispetto alle posizioni degli elettroni, sia rispetto ai loro spin. Anche in questo caso avremo uno stato di singoletto ψ+ con ms = 0 ed s = 0, e uno stato di tripletto ψ– con ms = 1 ed s = – 1, 0 o + 1. Per questo la funzione ψ+ è meglio conosciuta come ψs, e la ψ– come ψt:
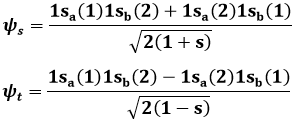
Per analogia con l'elio, si parla di paraidrogeno ed ortoidrogeno. Distinguerli è molto importante se, ad esempio, si vuole dare una corretta descrizione dei calori specifici dell'idrogeno molecolare. Così come per la molecola ione-idrogeno, si dimostra che è l'integrale di scambio k a decidere se la molecola è stabile oppure no: rappresentando le energie dei due stati sopra scritti, si trova un diagramma del tutto analogo a quello visto sopra per la molecola ione-idrogeno, anche se stavolta il valore dell'energia per R → ∞ (quando la molecola è dissociata) è il doppio di quello per la molecola ione-idrogeno, perchè qui abbiamo due elettroni, i quali possono dar vita a due atomi di idrogeno. Però l'energia dello stato di tripletto è sempre superiore a quella della molecola indissociata, dunque tale configurazione molecolare è instabile. L'energia di singoletto presenta invece una buca di potenziale, in cui la molecola di H2 può assumere una configurazione stabile. Dunque lo stato di singoletto è legante, il tripletto è antilegante. Sarà dunque nello stato di singoletto che noi osserveremo i due elettroni della molecola d'idrogeno. Se poi cercheremo il minimo di tale energia Es, lo troveremo in corrispondenza di R = 0,80 Å, in buon accordo con il dato sperimentale di 0,75 Å. Si può verificare che in questo caso la percentuale di legame ionico nella formazione della molecola è pari solo al 6 %. Si aggiunga il fatto che nel 1960 il polacco Włodzimierz Kołos (1928-1996) e l'olandese Clemens C. J. Roothaan (1918-) giunsero a prevedere il valore sperimentale con un errore di meno di un millesimo di elettronVolt, usando per la prima volta un calcolatore elettronico.
.
7.6 L'aufbau molecolare
Consideriamo ora una molecola costituita da due atomi differenti, ad esempio idrogeno e cloro; essi daranno vita ad acido cloridrico (HCl). Come si è visto, per la determinazione degli orbitali molecolari basta applicare il metodo LCAO e l'approssimazione adiabatica di Born-Oppenheimer; stavolta però non bisogna "mescolare" gli stati 1s, bensì orbitali più complicati, perchè l'idrogeno ha un solo elettrone nell'orbitale 1s, mentre il cloro (a parte gli orbitali 1s, 2s, 2p e 3s completi) ha sette elettroni nell'orbitale più esterno 2p. I calcoli diventano particolarmente laboriosi, ma concettualmente non c'è niente di nuovo. Se li si esegue con tutti i crismi, si può arrivare a formulare tre criteri generali con cui gli orbitali atomici si mescolano e danno vita ad orbitai molecolari. Essi sono detti "criteri di mescolamento", e di essi due sono di tipo qualitativo ed uno di tipo quantitativo:
PRIMO CRITERIO: nelle molecole omonucleari (cioè formate da atomi identici, come H2) gli orbitali molecolari si ottengono combinando linearmente orbitali identici, mentre in quelle eteronucleari (ad esempio HCl) gli orbitali molecolari si ottengono combinando orbitali atomici con la più simile situazione energetica dell'ultimo elettrone non legato.
SECONDO CRITERIO: gli orbitali atomici da combinare devono avere un alto grado di sovrapposizione spaziale (in altre parole, l'integrale di sovrapposizione deve essere molto grande)
TERZO CRITERIO: negli orbitali molecolari si deve conservare la componente del momento angolare lungo l'asse di legame.
I primi due criteri ci dicono come gli orbitali atomici devono combaciare tra di loro, a mò dei pezzi di un puzzle, per dare vita ad orbitali leganti, che assicurino la sopravvivenza delle molecole. Il terzo criterio, invece, ha una precisa interpretazione quantitativa: se gli orbitali non sono più sferici come 1s, non si conserva più il modulo quadrato del momento angolare; però il sistema è dotato di simmetria cilindrica intorno all'asse che passa per i due nuclei, in quanto la risultante della forza di attrazione che essi esercitano sull'elettrone giace in un qualsiasi piano passante per quest'asse, che indicheremo con il nome di asse z. Dunque è intuitivo che si debba conservare la componente Lz del momento angolare lungo tale asse, perchè tale forza di attrazione ha momento lungo l'asse di legame. Si devono perciò combinare funzioni d'onda con la stessa componente del momento angolare lungo l'asse di legame. Questo significa che negli orbitali molecolari non esiste un numero quantico che quantizza il modulo quadrato |L|2, ma solo un numero quantico che quantizza la componente Lz del momento angolare, numero quantico che indicheremo con λ. I suoi possibili valori sono λ = 0, ± 1, ± 2, ± 3... ed è l'equivalente del numero quantico magnetico m per l'atomo di idrogeno. Per gli orbitali molecolari infatti si usano lettere greche, per cui diremo che:
come ad l = 0 corrisponde l'orbitale atomico s, a λ = 0 corrisponde l'orbitale molecolare σ;
come ad l = 1 corrisponde l'orbitale atomico p, a λ = ± 1 corrisponde l'orbitale molecolare π;
come ad l = 2 corrisponde l'orbitale atomico d, a λ = ± 2 corrisponde l'orbitale molecolare δ;
come ad l = 3 corrisponde l'orbitale atomico f, così a λ = ± 3 corrisponde l'orbitale molecolare φ;
e così via: ad ogni lettera latina si sostituisce la lettera greca corrispondente. Tali orbitali però sono individuati dalla componente del momento angolare Lz lungo l'asse di legame, mentre quelli atomici erano individuati dal modulo quadrato del momento angolare. L'orbitale con λ = 0 e formato da una combinazione lineare di orbitali 1s si indica di solito con σ(1s). Gli orbitali antileganti si indicano con un asterisco.
Vediamo come arrivare a semplici orbitali molecolari applicando i criteri suddetti. Anzitutto, il terzo criterio ci dice che i due orbitali devono avere la stessa simmetria, altrimenti le forze non potrebbero giacere nel piano assiale della molecola, e tutto il ragionamento cadrebbe. Dunque vanno bene due orbitali 1s, esattamente come nella molecola d'idrogeno analizzata sopra. Gli orbitali 1s hanno la medesima simmetria sferica, dunque possono dar vita facilmente a due orbitali molecolari, che conosciamo già bene: se li combiniamo linearmente con il segno +, abbiamo l'orbitale legante (a) della figura sottostante, disegnata a mano libera dall'autore di questo sito, che è pari e quindi viene chiamato σg(1s) (la g sta per gerade). Se invece li combiniamo linearmente con il segno –, abbiamo l'orbitale antilegante (b) che presenta un nodo nel mezzo della congiungente i due nuclei, è dispari e quindi è indicato con la scrittura σu*(1s) (la u sta per ungerade).

Le cose sono molto simili simili se voglio combinare tra di loro orbitali di tipo p. Prendiamo anzitutto in considerazione gli orbitali pz. Essi sono distesi lungo l'asse che congiunge i nuclei, dunque in base al secondo criterio la sovrapposizione spaziale è molto alta, e si ottengono facilmente degli orbitali molecolari. Tali orbitali hanno l = 1, essendo di tipo p, però la proiezione di L su z è nulla, essendo m = 0 in entrambi gli orbitali da sovrapporre. Dunque, anche la loro sovrapposizione deve avere λ = 0. Se ne deduce che la combinazione di orbitali pz dà vita a un orbitale molecolare ancora di tipo σ! Scriveremo perciò σ(2p).

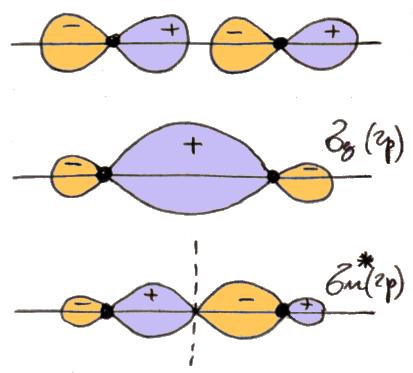
Sono gli orbitali px e py, con m ≠ 0, a dar vita ad orbitali di tipo π. Risolvendo l'opportuna equazione di Schrödinger si trova per essi una simmetria non più lobata, ma di tipo a ciambella, come si vede nella figura sottostante, sempre opera a mano libera dell'autore di questo sito:
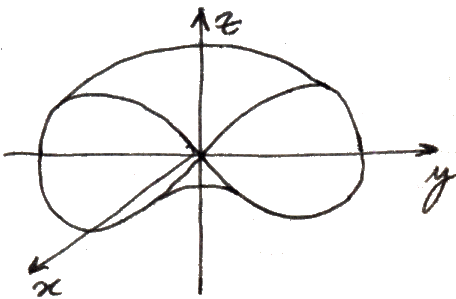
Purtroppo questi orbitali non soddisfano al secondo criterio, perchè non forniscono una sufficiente ricopertura: sono troppo sparpagliati nello spazio. È un po' come chiedere che aderiscano l'una contro l'altra due palle metalliche: aderiscono tanto meglio quanto più io le martello fino a che non presentano entrambe una faccia piatta. Allo stesso modo, perchè i due orbitali atomici si sovrappongano, occorre che presentino delle strutture lobate, simili agli orbitali pz. Ma come facciamo a "martellare" gli orbitali per far cambiare loro forma?
La risposta sta nel fatto che l'equazione di Schrödinger è lineare. Dunque, la combinazione lineare di due sue soluzioni è ancora una sua soluzione, e perciò anche la combinazione lineare di due funzioni d'onda ci dà un orbitale ammissibile. Combinando linearmente gli orbitali che abbiamo disegnato con opportuni coefficienti si trovano soluzioni del tutto differenti dalle precedenti, in cui scompare la simmetria attorno all'asse z e ricompaiono forme bilobate, con i lobi di segno opposto:

Ora tutti gli orbitali p assomigliano ai pz! Nonostante alcuni problemi dal punto di vista matematico, è proprio in questo stato che si trova l'elettrone quando nelle molecole si formano orbitali π. Infatti, gli orbitali px e py a forma di ciambella non potrebbero sovrapporsi adeguatamente ad altri per dae luogo ad orbitali molecolari. In pratica, l'energia complessiva della molecola è molto minore se gli elettroni si trovano in questi orbitali bilobati, che diremo p'x e p'y. Naturalmente l'elettrone "sceglie" automaticamente la configurazione quantistica in cui l'energia è minore, e così la nube elettronica cambia forma per adattarsi alle mutate condizioni fisiche. Le leggi della Meccanica Quantistica glielo permettono; e questo risulta una conferma del fatto, completamente generale, che il modo di descrivere uno stato quantistico dipende dalle condizioni del problema.
A questo punto, se combiniamo gli orbitali così ottenuti paralleli gli uni agli altri con gli stessi spin, otteniamo una situazione legante, con grossi lobi rafforzati, ma se li combiniamo con segni opposti, ho nuclei affacciati ed una evidente situazione antilegante. Questi orbitali hanno momento angolare complessivo ± 1, dunque sono di tipo π. Però, a differenza degli orbitali σ fin qui esaminati, quello legante è dispari, cioè ungerade, mentre quello antilegante è pari, cioè gerade. Questi orbitali perciò si chiamano rispettivamente πu(2p') e πg*(2p'). I risultati sono illustrati nella figura sottostante:

A questo punto ci siamo resi conto che le qualità degli orbitali non sono "cristallizzate" nello spazio e nel tempo come i personaggi del "Giudizio Universale" di Michelangelo nella Cappella Sistina: sono invece qualità dinamiche, in continuo mutamento per adattarsi allo stato del sistema considerato, e possono dar vita a un numero enorme di forme tridimensionali, alcune dall'aspetto veramente artistico! Passando dalla Fisica Atomica a quella Molecolare, la Natura ci ha rivelato un altro dei suoi aspetti inimmaginabili: la bellezza degli orbitali atomici, che già ci pareva superlativa, è stata surclassata dalla loro stessa capacità di autoreplicarsi e di dare vita a nuove forme, nuove architetture, nuove meraviglie di un universo ancora tutto da scoprire.
A questo punto, ci chiediamo: è possibile costruire una tabella degli orbitali molecolari, così come all'inizio di questo capitolo abbiamo costruito una tabella degli orbitali atomici? Bisogna mettere in ordine di energia crescente gli orbitali molecolari ora costruiti, come si vede nella figura sottostante. Come si vede, gli orbitali costruiti con gli 1s e 2s sono sistemati nella "scala energetica" in modo che gli orbitali leganti e antileganti si alternino. Passando alle combinazioni di orbitali 2p, invece, πu(2p) e σg(2p) hanno energie minori sia di πg*(2p) che di σu*(2p), come si può verificare risolvendo esplicitamente le equazioni. Su questa base, è possibile studiare l'aufbau, cioè il riempimento elettronico delle molecole più semplici.

Alla base della scala c'è evidentemente la molecola ione-idrogeno H2+, cui abbiamo dedicato uno dei paragrafi precedenti: abbiamo un solo elettrone nell'orbitale molecolare σg(1s), dunque la sua struttura sarà del tipo (σg(2p))1. La molecola di idrogeno H2 avrà invece due elettroni nel livello energetico più basso, cioè sempe in σg(1s); noi scriveremo perciò che la sua struttura è del tipo (σg(2p))2. Per sistemare ulteriori elettroni, occorre utilizzare un altro orbitale, perchè σg(1s) è saturo in base al Principio di Esclusione di Pauli, che ovviamente vale anche per gli orbitali molecolari. Dunque dobbiamo riempire l'orbitale con energia immediatamente superiore, cioè σu*(1s). Ma tale orbitale, come sappiamo, è antilegante. Tuttavia, si potrebbe dimostrare che una molecola è stabile finché ha più elettroni in stati leganti che antileganti. Infatti, il legame assicurato dagli orbitali leganti è allora sufficiente a neutralizzare la repulsione dovuta agli orbitali antileganti. In questo modo si tratta la cosiddetta molecola ione-elio, He2+. Essa ha necessariamente due elettroni nell'orbitale σg(1s), ed il terzo in σu*(1s). Naturalmente tale molecola è molto meno stabile di H2+ e di H2, ma può sussistere: il "desiderio" delle molecole di minimizzare la propria energia è tale che il terzo elettrone va a cercare l'orbitale antilegante, di energia inferiore, anziché il successivo orbitale legante, che lo costringerebbe ad un maggior sacrificio energetico! Se invece cercassi di realizzare una molecola biatomica di elio He2, dovrei mettere due elettroni nell'orbitale legante σg(1s) e due nell'orbitale antilegante σu*(1s); ciò però pregiudica la stabilità della molecola, che infatti non può sussistere: le molecole dei gas nobili sono sempre monoatomiche.
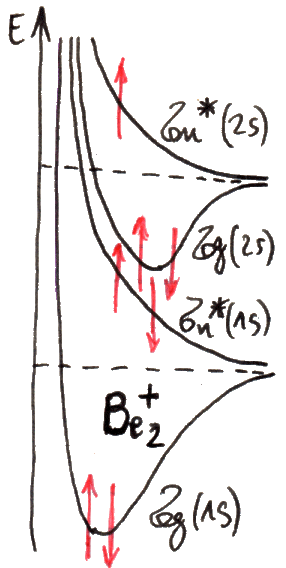 Passando
a molecole biatomiche omonucleari più complesse, il litio
all'equilibrio ha tre elettroni, quindi la molecola
ione-litio ha in tutto cinque elettroni ( 3 ∙ 2 – 1 ). Di questi,
quattro vanno negli orbitali derivati da 1s: due nel legante
σg(1s),
due nell'antilegante
σu*(1s);
il quinto deve giocoforza andare nell'orbitale legante
σg(2s),
del tutto simile a
σg(1s).
Dunque, la sua struttura è del tipo (σg(2s))2
(σu*(1s))2
(σg(2s))1.
Naturalmente la molecola di litio (Li2) completerà questo
orbitale: (σg(2s))2
(σu*(1s))2
(σg(2s))2.
Tale molecola effettivamente esiste, ma è reperibile solo nei
vapori del metallo, che allo stato solido
preferisce un'organizzazione di tipo cristallino.
Dopo il litio nella tavola periodica viene il berillio
(il suo nome deriva dal siriaco e significa "cristallo"). La molecola Be2+,
con sette elettroni, deve per forza piazzare l'ultimo di essi nell'orbitale
antilegante
σu*(2s),
come mostra la figura qui accanto. Tale molecola dunque può esistere, anche se è
piuttosto instabile, come He2+. Invece Be2
avrebbe quattro elettroni in orbitali leganti e quattro in orbitali antileganti,
e quindi non è stabile: infatti non può essere reperita neppure nei vapori del
metallo. E questo, senza che il berillio sia un gas nobile, perchè può formare
molecole eteronucleari come BeF2 o
fluoruro di berillio, e nello stato solido si presenta in forma
cristallina. Come si vede, l'impossibilità di costituire una molecola biatomica
omonucleare non dipende dal riempimento degli orbitali atomici (l'elio ha una
struttura elettronica esterna satura, il berillio no), ma da quello degli
orbitali molecolari! Una cosa dunque è l'atomo, un'altra la molecola. Quando due
atomi si fondono per dare vita a una molecola, i loro orbitali mutano, e muta
dunque anche il completamento rispetto a quelli che sono gli atomi isolati.
Passando
a molecole biatomiche omonucleari più complesse, il litio
all'equilibrio ha tre elettroni, quindi la molecola
ione-litio ha in tutto cinque elettroni ( 3 ∙ 2 – 1 ). Di questi,
quattro vanno negli orbitali derivati da 1s: due nel legante
σg(1s),
due nell'antilegante
σu*(1s);
il quinto deve giocoforza andare nell'orbitale legante
σg(2s),
del tutto simile a
σg(1s).
Dunque, la sua struttura è del tipo (σg(2s))2
(σu*(1s))2
(σg(2s))1.
Naturalmente la molecola di litio (Li2) completerà questo
orbitale: (σg(2s))2
(σu*(1s))2
(σg(2s))2.
Tale molecola effettivamente esiste, ma è reperibile solo nei
vapori del metallo, che allo stato solido
preferisce un'organizzazione di tipo cristallino.
Dopo il litio nella tavola periodica viene il berillio
(il suo nome deriva dal siriaco e significa "cristallo"). La molecola Be2+,
con sette elettroni, deve per forza piazzare l'ultimo di essi nell'orbitale
antilegante
σu*(2s),
come mostra la figura qui accanto. Tale molecola dunque può esistere, anche se è
piuttosto instabile, come He2+. Invece Be2
avrebbe quattro elettroni in orbitali leganti e quattro in orbitali antileganti,
e quindi non è stabile: infatti non può essere reperita neppure nei vapori del
metallo. E questo, senza che il berillio sia un gas nobile, perchè può formare
molecole eteronucleari come BeF2 o
fluoruro di berillio, e nello stato solido si presenta in forma
cristallina. Come si vede, l'impossibilità di costituire una molecola biatomica
omonucleare non dipende dal riempimento degli orbitali atomici (l'elio ha una
struttura elettronica esterna satura, il berillio no), ma da quello degli
orbitali molecolari! Una cosa dunque è l'atomo, un'altra la molecola. Quando due
atomi si fondono per dare vita a una molecola, i loro orbitali mutano, e muta
dunque anche il completamento rispetto a quelli che sono gli atomi isolati.
Quando dal berillio passiamo al boro, la differenza è sostanziale, perchè si passa agli orbitali π. Siccome tali orbitali hanno λ = ± 1, tali orbitali sono degeneri: uno costituito dagli orbitali atomici 2px e uno dai 2py. Tale livello di energia può dunque ospitare quattro elettroni, due con m = + 1 e spin opposti, due con m = – 1 e spin opposti. Il boro va a collocare due elettroni in πu(2p), che ne può contenere quattro e, per via della degenerazione, tali particelle possono presentarsi sia con spin paralleli che antiparalleli. In quest'ultimo caso, ms = 0, cioè stot = 0, e si parla di stato di singoletto; se sono paralleli, ms = 1 e stot = + 1; 0; – 1 ed è uno stato di tripletto. Possiamo benissimo chiamarli paraboro e ortoboro. Naturalmente nell'ortoboro, dove gli spin sono paralleli, un elettrone si trova in πu(2p+1), uno in πu(2p–1), per non violare il principio di Pauli. Siccome gli spin tendono a disporsi paralleli gli uni agli altri, è favorito energeticamente lo stato di tripletto. Il carbonio (C2) completa con altri due elettroni l'orbitale . Il momento angolare totale può essere solo nullo, quindi è possibile il solo stato di singoletto. La molecola di azoto (N2) si riempie con due elettroni il successivo orbitale molecolare σg(2pz), che è ancora legante. Abbiamo ben sei elettroni in orbitali leganti, dunque tale molecola è da considerarsi particolarmente stabile. Con una simbologia che in chimica è nota come formula di struttura, che indica ogni legame con un trattino (–), tale molecola è indicata con la scrittura N≡N, giacché il legame in gioco è triplo: due legami sono di tipo π ed uno di tipo σ, occupati da due elettroni leganti detti elettroni di legame. I successivi orbitali antileganti sono molto lontani energeticamente da quelli occupati, ed è difficile che gli elettroni li raggiungano per eccitazione. Ciò sèiega perchè tali molecole sono tanto riluttanti ad aggregarsi ulteriormente, e restano allo stato gassoso fino a bassissime temperature: l'azoto liquefa solo a – 196°C, ad opera di forze dette di Van der Waals.
 Dopo
l'azoto viene l'ossigeno (O2). I suoi due elettroni devono per
forza andare nell'orbitale antilegante πg*(2p),
per cui la sua struttura è nel complesso più instabile
di quella dell'azoto. Mentre l'azoto ha un momento angolare totale nullo, cioè
si trova nel solo stato di singoletto, come il
carbonio, l'ossigeno può avere i due elettroni antileganti entrambi in
πg*(2p+1),
o entrambi in
πg*(2p–1),
o uno nell'uno, uno nell'altro. Ciò significa che possiamo avere sia lo stato di
singoletto (paraossigeno),
sia di tripletto (ortoossigeno),
con quest'ultimo energeticamente favorito. Dunque l'ossigeno denota la presenza
di un momento di spin, e questo spiega perchè
l'ossigeno è paramagnetico, mentre l'azoto è
diamagnetico. Inoltre, l'ossigeno ha ancora due
elettroni liberi in questo orbitale, anche se esso è sntilegante, e dunque può
reagire con altri atomi, formando ad esempio la molecola di
ozono (O3), che è il gas
che si sprigiona quando accendiamo un fiammifero, facilmente riconoscibile per
il suo odore penetrante, e che, essendo opaco ai raggi
ultravioletti, costituisce la barriera che salva la vita sulla Terra dai
pericolosi ultravioletti sprigionati dal Sole: si forma infatti nell'alta
atmosfera, ad opera dei raggi cosmici che collidono con le molecole di O2,
formando l'O3. Proprio l'assottigliarsi di questo
strato di ozono, il famoso "buco dell'ozono" sopra
il Polo Sud (vedi foto a fianco), creò tanta preoccupazione agli scienziati
negli anni Ottanta del secolo scorso, e contribuì alla messa al bando dei
clorofluorocarburi, molecole usate come propellente
spray e gravemente dannose per l'ozono atmosferico, con il Protocollo di
Montréal (firmato il 16 settembre 1987).
Dopo
l'azoto viene l'ossigeno (O2). I suoi due elettroni devono per
forza andare nell'orbitale antilegante πg*(2p),
per cui la sua struttura è nel complesso più instabile
di quella dell'azoto. Mentre l'azoto ha un momento angolare totale nullo, cioè
si trova nel solo stato di singoletto, come il
carbonio, l'ossigeno può avere i due elettroni antileganti entrambi in
πg*(2p+1),
o entrambi in
πg*(2p–1),
o uno nell'uno, uno nell'altro. Ciò significa che possiamo avere sia lo stato di
singoletto (paraossigeno),
sia di tripletto (ortoossigeno),
con quest'ultimo energeticamente favorito. Dunque l'ossigeno denota la presenza
di un momento di spin, e questo spiega perchè
l'ossigeno è paramagnetico, mentre l'azoto è
diamagnetico. Inoltre, l'ossigeno ha ancora due
elettroni liberi in questo orbitale, anche se esso è sntilegante, e dunque può
reagire con altri atomi, formando ad esempio la molecola di
ozono (O3), che è il gas
che si sprigiona quando accendiamo un fiammifero, facilmente riconoscibile per
il suo odore penetrante, e che, essendo opaco ai raggi
ultravioletti, costituisce la barriera che salva la vita sulla Terra dai
pericolosi ultravioletti sprigionati dal Sole: si forma infatti nell'alta
atmosfera, ad opera dei raggi cosmici che collidono con le molecole di O2,
formando l'O3. Proprio l'assottigliarsi di questo
strato di ozono, il famoso "buco dell'ozono" sopra
il Polo Sud (vedi foto a fianco), creò tanta preoccupazione agli scienziati
negli anni Ottanta del secolo scorso, e contribuì alla messa al bando dei
clorofluorocarburi, molecole usate come propellente
spray e gravemente dannose per l'ozono atmosferico, con il Protocollo di
Montréal (firmato il 16 settembre 1987).
Osserviamo che la successiva molecola di questo tipo, quella di fluoro (F2), si forma riempiendo l'orbitale πg*(2p); la molecola può sussistere, perchè ha sei elettroni leganti e quattro antileganti. La sua energia di dissociazione (l'energia necessaria per dividerla nei suoi atomi componenti) è minore di quella dell'ossigeno, a sua volta minore di quella dell'azoto, perchè continuiamo ad aggiungere elettroni in orbitali antileganti. Naturalmente la molecola di neon (Ne2) andrebbe a riempire anche l'orbitale antilegante σu*(2pz); avremmo sei elettroni leganti e sei antileganti, e la molecola non può sussistere. Abbiamo così completato la rassegna degli orbitali molecolari costruiti con orbitali atomici identici delle prime due shell energetiche delle molecole omonucleari; le loro strutture sono elencate qui sotto, dove (He2) e (Be2) indicano rispettivamente le strutture elettroniche delle ipotetiche molecole di elio e berillio, altrimenti le formule sarebbero diventate troppo lunghe, così come facevamo nel § 7.1 con le strutture dei gas nobili:
| H2+
(σg(1s))1 H2 (σg(1s))2 He2+ (σg(1s))2 (σu*(1s))1 He2 (σg(1s))2 (σu*(1s))1 instabile Li2+ (He2) (σg(2s))1 Li2 (He2) (σg(2s))2 Be2+ (He2) (σg(2s))2 (σu*(2s))1 Be2 (He2) (σg(2s))2 (σu*(2s))2 instabile B2+ (Be2) (πu(2p))1 B2 (Be2) (πu(2p))2 C2+ (Be2) (πu(2p))3 C2 (Be2) (πu(2p))4 N2 (Be2) (πu(2p))4 (σg(2pz))2 O2 (Be2) (πu(2p))4 (σg(2pz))2 (πg*(2p))2 F2 (Be2) (πu(2p))4 (σg(2pz))2 (πg*(2p))2 Ne2 (Be2) (πu(2p))4 (σg(2pz))2 (πg*(2p))2 (σu*(2pz))2 instabile |
.
7.7 Tre molecole misteriose
Diamo ora un'occhiata agli orbitali delle molecole eteronucleari, costruite cioè con atomi di specie diversa, che poi sono la maggioranza delle molecole. Continuano a valere i tre criteri di miscelamento del § 7.6, ma compare una novità, nota come ibridizzazione. Per spiegare questo concetto, useremo tre notissimi esempi di molecole poliatomiche eteronucleari: le molecole di acqua (H2O), ammoniaca (NH3) e metano (CH4).
Partiamo con l'acqua, il composto al quale si deve la nostra stessa esistenza. Si è visto che l'ossigeno ha due elettroni nell'orbitale atomico 1s, due nell'orbitale 2s e quattro negli orbitali 2p; se gli elettroni si disponessero con tutti gli spin antiparalleli, avremmo un orbitale del tutto vuoto e nessuna possibilità di legame. Tuttavia, per la regola di Hund, l'energia è minima se essi si dispongono con il massimo numero possibile di spin paralleli. Se è così, gli orbitali 2p0 e 2p+1 sono occupati da un solo elettrone ciascuno, e possono formare orbitali molecolari con altri due orbitali occupati da un elettrone ciascuno; se essi appartengono a un altro atomo di ossigeno, si ottiene appunto la molecola O2, i cui orbitali abbiamo studiato per filo e per segno. Ma supponiamo che questi due elettroni appartengono ad altrettanti atomi di idrogeno. Possiamo supporre che gli elettroni di tali atomi siano nello stato fondamentale, cioè 1s. Il legame che si viene a creare nella molecola di idrogeno è perciò quello che si vede nella figura sottostante: l'elettrone 1s del primo idrogeno deve formare legame con l'elettrone 2p0 dell'ossigeno, mentre l'elettrone 1s del secondo idrogeno deve formare legame con l'elettrone 2p+1 dell'ossigeno. Dobbiamo perciò mescolare tra di loro orbitali diversi, 1s e 2p.
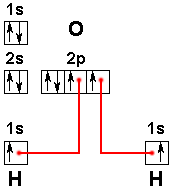

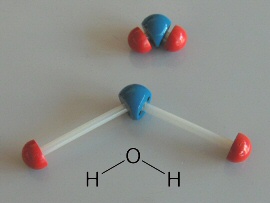
Questa rappresentazione non mette affatto in evidenza l'effettiva forma del legame nello spazio. Ragioniamo insieme: vale lo stesso discorso fatto per i legami π(2p'). Se io utilizzassi gli orbitali p+1 e p–1 a forma di ciambella, la sovrapposizione spaziale di questi con gli orbitali sferiformi 1s non sarebbe buona, e quindi l'energia sarebbe maggiore che nel caso in cui si usassero le loro combinazioni lineari 2p'x e 2p'y. Sono perciò questi, bilobati come 2pz, ad intervenire nel legame della molecola d'acqua. Supponiamo che l'orbitale 2p'y sia tutto pieno: esso non interviene nel legame. In gioco ci sono allora gli orbitali 2p'x e 2p'z. Combinandoli con 1s con segno positivo, trovo un solo grande lobo con l'elettrone spessissimo presente tra i due nuclei, e perciò con funzione di collante; tale orbitale è legante. Se invece la combinazione avviene con segno negativo, l'elettrone non è quasi mai presente tra i due nuclei, l'orbitale è antilegante, e addio molecola d'acqua. Ora, però, se le cose andassero così, i due legami O–H dovrebbero formare tra di loro un angolo di 90°. Invece, con metodi come la diffrazione di neutroni si è potuto appurare che i due legami O–H nella molecola d'acqua sono separati da un angolo di 104°,45. Dunque la teoria della combinazione lineare degli orbitali atomici qui cade in fallo, non coincidendo più con l'esperienza. E non è un caso isolato.
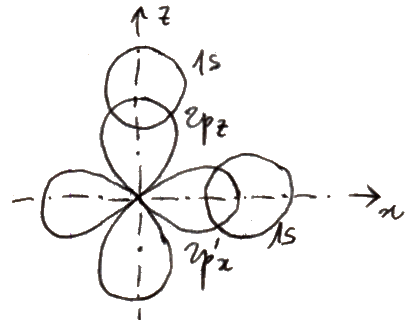
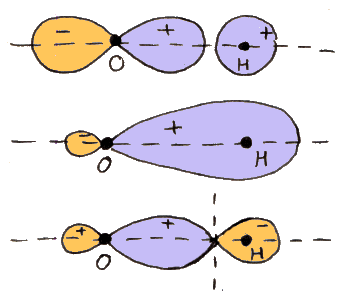
Infatti, consideriamo la molecola di ammoniaca (NH3). L'azoto ha due elettroni in 1s, due in 2s e tre in 2p; questi ultimi, per il Principio di Hund, si dispongono tutti con spin paralleli, uno in 2p–1, uno in 2p0 ed uno in 2p+1, e così ho tre possibilità di legame: la chimica ci dice che in questo caso ha valenza tre. Con altrettanti atomi di idrogeno, si forma proprio l'atomo di NH3:



I tre orbitali leganti N–H sarebbero però diretti lungo i tre assi cartesiani x, y e z, così come 2p'x, 2p'y e 2p'z, a 90° l'uno dall'altro. Anche in questo caso le osservazioni sperimentali ci danno torto: fra i tre legami N–H di NH3 gli spettroscopisti misurano angoli di 107°,8. Il mistero si infittisce.
E si infittisce ancora di più, se pensiamo alla molecola di metano (CH4). Il carbonio ha due elettroni in 1s, due in 2s e due in 2p. Siccome la differenza energetica tra 2s e 2p è scarsa, è possibile che uno dei due elettroni 2s salti nell'orbitale libero tra i tre 2p. Così, oltre che valenza due (due orbitali 2p parzialmente occupati), il carbonio può avere anche valenza quattro (un orbitale 2s e tre 2p parzialmente occupati). Se queste quattro valenze vengono occupate da altrettanti atomi di idrogeno, si ottiene la molecola di metano. Tre di questi legami C–H dovrebbero essere di tipo 1s – 2p, dunque dovrebbero essere orientati a 90° l'uno dall'altro lungo gli assi cartesiani; uno è di tipo 1s – 2s e, siccome tali orbitali sono sferici, questo legame dovrebbe essere orientato casualmente nello spazio rispetto agli altri tre. Tale situazione è manifestamente anisotropa, ed infatti la Natura la rifiuta. Le osservazioni sperimentali ci dicono che i quattro legami C–H sono disposti in modo isotropo nello spazio, cioè a distanze uguali l'uno dall'altro, e quindi gli angoli tra di essi sono pari a 109°,5. Infatti la molecola di metano ha la forma di un tetraedro regolare (la forma che aveva una volta il cartone del latte), con l'atomo di carbonio nel mezzo e i quattro di idrogeno ai tre vertici, come si vede qui sotto. Quanto abbiamo studiato finora non è in grado di dare una spiegazione a queste molecole misteriose.

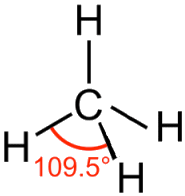

Nel condurre questo
ragionamento, noi non abbiamo tenuto conto di un particolare. Abbiamo visto che,
nelle molecole omonucleari, le funzioni d'onda possono essere solo
pari o dispari
rispetto all'inversione delle coordinate spaziali, cioè
gerade o ungerade. Orbene, per molecole
eteronucleari non è più così. Infatti in queste molecole
la distribuzione di densità di carica non è più necessariamente simmetrica.
Ciò significa che il baricentro delle cariche positive non coincide più con il
baricentro delle cariche negative! Le molecole che si formano così sono dette
polari, perchè sono dotate di un
momento di dipolo
 permanente. Questo è il motivo
per cui, mentre le molecole biatomiche omonucleari, dotate di distribuzioni
simmetriche di carica, sono recalcitranti a formare ulteriori legami, le
molecole polari tendono ad aggregarsi con legami dipolo-dipolo. Per descrivere
questo comportamento, il grande chimico americano Linus
Pauling (1901-1994), due volte premio Nobel, introdusse nel 1928 il
concetto di elettronegatività.
Qualitativamente parlando, essa è la tendenza, da parte di un atomo di attirare
a sé gli elettroni in una molecola. Per capire cosa ciò significhi, aiutiamoci
con un piccolo esperimento. Apriamo un comune rubinetto da cucina e facciamo
uscire da esso un sottile filo d'acqua. Avvicinando ad esso una
bacchetta di vetro strofinata con un panno di lana,
e perciò caricata positivamente, il flusso d'acqua
viene deviato ed attirato dalla bacchetta, come si vede qui sotto a sinistra. E la stessa cosa avviene con una
bacchetta di plastica, che si carica
negativamente. Perchè? La risposta sta nel fatto
che la molecola d'acqua è polare. L'ossigeno è più
elettronegativo dell'idrogeno, cioè attira a sé gli elettroni più strettamente,
in modo che le funzioni d'onda dei corrispondenti orbitali molecolari non sono
né pari né dispari rispetto all'inversione delle coordinate spaziali, ma si
addensano maggiormente sull'atomo di ossigeno: è più probabile trovare lì
l'elettrone, che non sugli atomi di idrogeno, come la famosa coperta troppo
corta: se me la tiro sul mento, mi lascia scoperti i piedi. Allo stesso modo,
gli atomi di idrogeno restano "scoperti" di elettroni, e
su di essi prevale la carica positiva, mentre sull'atomo d'ossigeno prevale
quella negativa. I baricentri delle due cariche non coincidono più, e la
molecola presenta un momento di dipolo elettrico permanente. Dunque basta una
bacchetta caricata per strofinio, sia di segno positivo che negativo,
per deviare un flusso di molecole d'acqua. Invece, come si vede qui sotto a
destra, un liquido non polare come alcool etilico a acetone non vengono affatto
deviati dalla bacchetta caricata, perchè essi sono privi di momento di dipolo
elettrico permanente.
permanente. Questo è il motivo
per cui, mentre le molecole biatomiche omonucleari, dotate di distribuzioni
simmetriche di carica, sono recalcitranti a formare ulteriori legami, le
molecole polari tendono ad aggregarsi con legami dipolo-dipolo. Per descrivere
questo comportamento, il grande chimico americano Linus
Pauling (1901-1994), due volte premio Nobel, introdusse nel 1928 il
concetto di elettronegatività.
Qualitativamente parlando, essa è la tendenza, da parte di un atomo di attirare
a sé gli elettroni in una molecola. Per capire cosa ciò significhi, aiutiamoci
con un piccolo esperimento. Apriamo un comune rubinetto da cucina e facciamo
uscire da esso un sottile filo d'acqua. Avvicinando ad esso una
bacchetta di vetro strofinata con un panno di lana,
e perciò caricata positivamente, il flusso d'acqua
viene deviato ed attirato dalla bacchetta, come si vede qui sotto a sinistra. E la stessa cosa avviene con una
bacchetta di plastica, che si carica
negativamente. Perchè? La risposta sta nel fatto
che la molecola d'acqua è polare. L'ossigeno è più
elettronegativo dell'idrogeno, cioè attira a sé gli elettroni più strettamente,
in modo che le funzioni d'onda dei corrispondenti orbitali molecolari non sono
né pari né dispari rispetto all'inversione delle coordinate spaziali, ma si
addensano maggiormente sull'atomo di ossigeno: è più probabile trovare lì
l'elettrone, che non sugli atomi di idrogeno, come la famosa coperta troppo
corta: se me la tiro sul mento, mi lascia scoperti i piedi. Allo stesso modo,
gli atomi di idrogeno restano "scoperti" di elettroni, e
su di essi prevale la carica positiva, mentre sull'atomo d'ossigeno prevale
quella negativa. I baricentri delle due cariche non coincidono più, e la
molecola presenta un momento di dipolo elettrico permanente. Dunque basta una
bacchetta caricata per strofinio, sia di segno positivo che negativo,
per deviare un flusso di molecole d'acqua. Invece, come si vede qui sotto a
destra, un liquido non polare come alcool etilico a acetone non vengono affatto
deviati dalla bacchetta caricata, perchè essi sono privi di momento di dipolo
elettrico permanente.

Linus Pauling introdusse anche una definizione quantitativa di elettronegatività. Si può verificare che, se non c'è differenza di elettronegatività tra due atomi diversi A e B (es. tra idrogeno e fosforo), l'energia di legame, cioè la profondità della buca di potenziale, è la media geometrica dell'energia di legame delle molecole biatomiche omonucleari A–A e B–B:
![]()
In presenza di una differenza di elettronegatività, EAB è diverso da tale media geometrica. Chiamiamo tale differenza ΔEAB:
![]()
con ΔEAB > 0. Più la polarità delle molecole cresce, più ΔEAB aumenta. Pauing ipotizzò allora una proporzionalità diretta fra le elettronegatività x dei due atomi del legame e l'eccesso ΔEAB:
![]()
Questa ipotesi si rivelò sbagliata. Infatti, se A, B e C sono tre atomi diversi, si deve avere:

Sommando membro a membro le prime due si ha:
![]()
e confrontandola con la terza:
![]()
Ora, i risultati sperimentali non concordano con questa relazione. È piuttosto vero che:
![]()
Dunque, | xA – xB | non è proporzionale a ΔEAB, ma alla sua radice quadrata. Pauling identificò | xA – xB | con la radice quadrata di misurata in elettronVolt:
![]()
In base a questa relazione possiamo stabilire una scala relativa di elettronegatività. Per arrivare a dei valori assoluti, dobbiamo stabilire un riferimento. Pauling decise di assumere come valore di elettronegatività di un certo atomo quello che esso assume nel legarsi con l'idrogeno, cui egli attribuì il valore xH = 2,1 in modo da non avere a che fare con valori negativi. È così possibile determinare l'elettronegatività di ogni elemento secondo Pauling. Io ne ho elencate trentadue nella tabella seguente:
|
H |
2,20 |
Na |
0,93 |
Ca |
1,00 |
Ag |
1,93 |
|
Li |
0,98 |
Mg |
1,31 |
Cr |
1,66 |
Cd |
1,69 |
|
Be |
1,57 |
Al |
1,61 |
Fe |
1,83 |
I |
2,66 |
|
B |
2,04 |
Si |
1,90 |
Co |
1,88 |
Au |
2,54 |
|
C |
2,55 |
P |
2,19 |
Ni |
1,91 |
Hg |
2,00 |
|
N |
3,04 |
S |
2,58 |
Cu |
1,90 |
Fr |
0,70 |
|
O |
3,44 |
Cl |
3,16 |
Zn |
1,65 |
Ra |
0,90 |
|
F |
3,98 |
K |
0,82 |
Br |
2,90 |
U |
1,38 |
Si osserva che essa diminuisce percorrendo i gruppi della tabella periodica verso il basso, poiché allora aumenta la carica nucleare, ma l'attrazione del nucleo sugli elettroni più esterni è schermata da quelli delle shell più interne. Invece, l'elettronegatività aumenta percorrendo i gruppi da sinistra a destra, perchè ci avviciniamo a strutture elettroniche più stabili, con gli orbitale esterni completi. In conseguenza di questo andamento, l'elemento più elettronegativo è il fluoro, mentre quello meno elettronegativo, o più elettropositivo come talvolta si dice, è il francio.
L'esistenza dell'elettronegatività spiega, almeno in parte, la struttura della molecola d'acqua. Infatti, essendo l'ossigeno più elettronegativo dell'idrogeno di quasi un'unità e mezza, cioè del 75 %, la molecola d'acqua risulta fortemente polare; i due atomi di idrogeno risultano "scoperti" di elettroni e si affacciano con i loro nuclei positivi. Essi tendono allora a respingersi, e ciò può spiegare perchè l'angolo tra i legami O–H è pari a 104°,45 e non a 90°. La stessa cosa può dirsi per la molecola di ammoniaca, dove a respingersi sono tre atomi di idrogeno, e quindi la divaricazione è maggiore. Come prova di questo fatto, si può addurre il confronto tra queste molecole e due molto simili ad esse: l'acido solfidrico (H2S) e la fosfina (PH3). L'ossigeno e lo zolfo hanno struttura elettronica esterna assai simile, appartenendo allo stesso gruppo della Tavola Periodica. Però i rispettivi elettroni di legame sono più lontani dai nuclei nello zolfo che nell'ossigeno, dunque i nuclei resterebbero "meno scoperti" e la repulsione è minore: infatti l'angolo tra i due legami S–H è solo di 92°,1. Lo stesso discorso vale per la fosfina: fosforo e azoto sono molto simili, ma l'elettronegatività del fosforo è minore, dunque la repulsione è minore. L'angolo tra i legami è pari a soli 93°,5 contro i 109°,5 dell'ammoniaca.
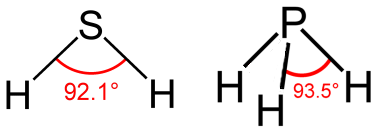
Però è facile rendersi conto che questo ragionamento non è in grado di spiegare il comportamento della molecola di metano, in cui non ci sono legami la cui direzione è lasciata al caso, come invece dovrebbe essere per l'orbitale 1s – 2s. La nostra impressione è che la struttura della molecola di metano comporti l'identità di tutti e quattro i legami C–H, indipendentemente dal fatto che siano originati da orbitali atomici 2s o 2p. Linus Pauling allora si spinse più avanti, e introdusse gli orbitali ibridi. Nella loro corsa verso la minima energia possibile, gli elettroni scelgono opportune combinazioni lineari di orbitali, in modo che i quattro orbitali 2s, 2p'x, 2p'y, 2p'z abbiano più o meno la stessa forma. Le combinazioni lineari sono le seguenti:
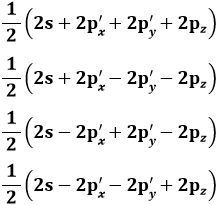
Naturalmente 1/2 serve per la normalizzazione. La forma di questo orbitale è illustrata qui sotto a sinistra: un lobo si "atrofizza", l'altro invece si ingrandisce a dismisura. Se cerchiamo di calcolare la direzione angolare di questi orbitali, scopriamo che i loro assi sono diretti lungo i vertici di un tetraedro regolare, come si vede qui sotto a destra. Dunque è proprio questa la configurazione che consente la formazione di una molecola di metano, perchè questi grossi monolobi sembrano fatti apposta per realizzare legami con gli orbitali 1s dell'idrogeno!
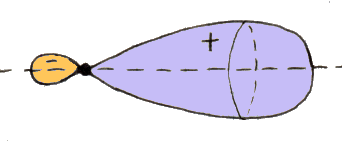

Questi nuovi orbitali però non possono più essere chiamati né s né p: sono completamente diversi dagli ordinari orbitali atomici, però la Natura li sceglie perchè sono utili per minimizzare l'energia. Noi li chiameremo orbitali ibridi sp3, essendo derivati dalla combinazione lineare di un orbitale s e di tre orbitali p. Quando gli orbitali atomici si "rimescolano" per dar vita ad orbitali nuovi distribuiti in modo isotropo nello spazio, onde minimizzare l'energia delle molecole in formazione, si parla di ibridizzazione degli orbitali atomici. Questa ipotesi è l'unica in grado di spiegare perchè nella molecola di metano i quattro legami C–H sono separati da angoli di 109°,5; e non solo.
Infatti, altre molecole possono essere spiegate solo ricorrendo all'ipotesi dell'ibridizzazione. È questo il caso dell'etilene o etene, il più semplice degli alcheni, avente formula bruta C2H4. A temperatura ambiente si presenta gassoso, incolore e fortemente infiammabile, e nell'industria chimica è usato per produrre il polietilene. La sua formula di struttura è la seguente, costruita con appositi modellini:

Come si vede, ha la forma di una chiave inglese, ed i legami C–C e C–H sono separati di angoli di 120°. Anche questo tipo di orbitale resiste ad ogni interpretazione, a meno che gli orbitali 2s, 2p'x e 2p'y del carbonio non siano ibridati tra loro secondo le formule seguenti:

Gli orbitali hanno la stessa forma monolobata vista nel caso precedente, ma stavolta sono tre e sono separati tra loro da angoli di 120°. Infatti, mentre la molecola di metano è tridimensionale, quella di etilene è piana. Due di questi lobi formano legami con orbitali 1s dell'idrogeno, uno invece lo forma con un orbitale dello stesso tipo di un altro atomo di carbonio, mentre restano due orbitali 2pz non ibridati, che formano orbitali π ortogonalmente al piano molecolare. In tal caso si parla di ibridizzazione di tipo sp2, perchè ad essere miscelati sono due orbitali p ed uno s!

Infine, consideriamo la molecola di acetilene o etino, il più semplice degli alchini, scoperto nel 1836 dal chimico inglese Edmund Davy (1785-1857). È un idrocarburo alifatico insaturo fortemente esplosivo, con formula bruta C2H2. A temperatura e pressione standard è un gas incolore ed estremamente infiammabile; è da considerarsi estremamente pericoloso perché può esplodere anche con inneschi minimi, e per questo è normalmente diluito nell'acetone. Viene usato per la saldatura e il taglio dei metalli, dato che la sua combustione con l'ossigeno produce una fiamma la cui temperatura arriva fino a 3300 °C. L'acetilene è anche utilizzato nei dispositivi di illuminazione utilizzati dagli speleologi. La sua formula di struttura, ricostruita con un apposito kit disponibile presso i laboratori scolastici di chimica, è la seguente:

Evidentemente, come tra i due atomi di carbonio dell'etilene c'era un legame doppio (tra due sp2 e tra due pz), qui tra i due atomi di carbonio deve esserci un legame triplo, evidenziato dalle tre bacchette che li collegano nel modellino soprastante. Questa struttura è spiegabile se pensiamo a una combinazione lineare tra 2s e 2p'x, del tipo:
![]()
Uno dei due lobi del si atrofizza, l'altro si amplifica, come si vede qui sotto. Si parla in tal caso di ibridizzazione di tipo sp, perchè si mescola un orbitale di tipo p con uno di tipo s. Lo stesso tipo di ibridizzazione giustifica molte altre molecole lineari, come ad esempio l'anidride carbonica (CO2).

Nella molecola di acetilene i due lobi così ottenuti sono rivolti in direzioni opposte, uno di essi forma legame con l'orbitale 1s dell'idrogeno, l'altro con un altro orbitale di questo tipo dell'altro atomo di carbonio. I due orbitali restanti, del tipo p'x e pz, formano tra di loro legami ortogonalmente alla linea della molecola, come si vede nel disegno a mano libera qui sotto:
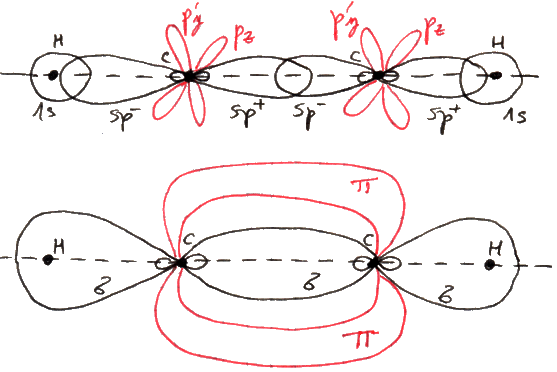
Vi sono casi di molecole in cui lo stesso elettrone è condiviso da molti atomi, ma a questo argomento dedicheremo l'ultimo paragrafo di questo lungo capitolo.
.
7.8 Cristalli ionici e cristalli covalenti
Abbiamo visto che gli atomi non si trovano quasi mai in Natura isolati l'uno dall'altro, ma tendono spontaneamente ad organizzarsi in molecole e in altri aggregati; e questi a loro volta si riuniscono fra di loro a dare vita ai cosiddetti stati di aggregazione della materia, i più semplici dei quali sono lo stato solido, liquido ed aeriforme. Tutta questa spiccata "attività sociale" degli atomi è possibile grazie ai legami chimici. Secondo la definizione data da Gilbert Newton Lewis (1875-1946), Walter Heinrich Heitler (1904-1981) e Wolfgang Fritz London (1900-1954), il legame chimico è la messa in comune di elettroni fra atomi diversi, eseguita allo scopo di raggiungere configurazioni elettroniche stabili. Infatti abbiamo visto che i più stabili fra tutti gli elementi sono quelli con la struttura elettronica esterna del tutto occupata, cioè i gas nobili; infatti i loro orbitali hanno complessivamente energia inferiore a quella degli altri elementi,
Il modo più semplice che gli atomi hanno a disposizione per realizzare questo obiettivo è quello di mettersi assieme, esattamente come due piccole società possono raggiungere il pareggio del bilancio o conseguire guadagni maggiori se si fondono in una sola, più grande. Per essere più precisi, lo scopo delle "società atomiche" è sempre quello di completare l'ottetto elettronico esterno. Se ricordiamo quanto detto nel § 7.1, ci renderemo conto che gli strati esterni degli atomi non sono mai di tipo d, f o g, ma sempre di tipo s o p; prima di riempire gli orbitali con l > 2 di una shell, gli atomi riempiono quelli con l = 0 o l = 1 delle shell successive. Se perciò piazzo due elettroni nell'orbitale s più esterno e sei in quello di tipo p, ho ottenuto il risultato di "simulare" la struttura elettronica degli stabilissimi gas nobili. Tale regola è conosciuta in chimica come regola di Kossel o regola dell'ottetto (del "duetto" nel caso della sola molecola di idrogeno H2, dove lo strato elettronico esterno è costituito da due soli elettroni.
Ad esempio, questa regola è soddisfatta sia nel caso del metano (CH4) che del sale da cucina (NaCl). La differenza tra questi due composti sta nel modo in cui si perviene a questo completamento dell'ottetto. Infatti il carbonio, che nella shell più esterna ha due elettroni 2s e due elettroni 2p, si trova ad avere quattro elettroni esterni, e acquistandone quattro da altrettanti atomi di idrogeno riesce a realizzare il suo scopo. Altrettanto profitto ne traggono i quattro idrogeni, che con i quattro elettroni del carboni, uno per ogni diverso orbitale, completano il proprio duetto. Questo, però, a patto che gli elettroni siano contati due volte: una volta per un atomo, un'altra volta per l'altro. Questo perchè l'orbitale dell'uno e l'orbitale dell'altro atomo si fondono, come visto in precedenza, in un unico orbitale molecolare, che avvolge entrambi i nuclei, e quindi quest'orbitale è occupato da due elettroni (e perciò saturo) sia per un atomo che per l'altro.
 Questo curioso fatto può
essere visualizzato con la cosiddetta rappresentazione di
Lewis, dal nome del chimico americano Gilbert
Newton Lewis (1875-1946), che la propose nel 1916. In tale
rappresentazione, attorno al simbolo dell'elemento si mettono tanti
puntini quanti sono gli elettroni della shell più
esterna. Come si vede a fianco, un elettrone dell'idrogeno e uno del metano
formano un solo orbitale molecolare. L'idrogeno ha così due elettroni, e il
carbonio in tutto otto. Questo tipo di legame, basato sulla formazione di
orbitali molecolari e sulla messa in società di elettroni da parte di atomi
diversi, si dice legame covalente, perchè
gli elettroni di legame sono chiamati anche "di valenza".
Questa è la situazione che si presentava nella molecola di idrogeno (§
7.5) per le funzioni d'onda che condividono i due elettroni.
Questo curioso fatto può
essere visualizzato con la cosiddetta rappresentazione di
Lewis, dal nome del chimico americano Gilbert
Newton Lewis (1875-1946), che la propose nel 1916. In tale
rappresentazione, attorno al simbolo dell'elemento si mettono tanti
puntini quanti sono gli elettroni della shell più
esterna. Come si vede a fianco, un elettrone dell'idrogeno e uno del metano
formano un solo orbitale molecolare. L'idrogeno ha così due elettroni, e il
carbonio in tutto otto. Questo tipo di legame, basato sulla formazione di
orbitali molecolari e sulla messa in società di elettroni da parte di atomi
diversi, si dice legame covalente, perchè
gli elettroni di legame sono chiamati anche "di valenza".
Questa è la situazione che si presentava nella molecola di idrogeno (§
7.5) per le funzioni d'onda che condividono i due elettroni.
Ben diverso è il caso del
cloruro di sodio: in questo caso il cloro, cui manca un elettrone solo per
completare l'ottetto, strappa letteralmente l'elettrone al sodio, che ha un solo
elettrone nello strato esterno, e si formano due ioni, la cui attrazione
reciproca li tiene uniti. Il cloro è contento, perchè con l'elettrone in pi ha
completato l'ottetto esterno, e lo è parimenti il sodio perchè, avendo perso
l'unico elettrone nella shell M che possedeva, esibisce l'ottetto
completo nella sottostante shell L. Infatti, come si è
visto, per separare gli ioni Na+ e Cl–
occorre compiere lavoro, contrariamente a quanto accade per gli ioni H+
ed H– di H2. Questo prende il nome di
legame ionico.
Esso non dà vita a molecole, bensì ad aggregati più complessi, noti come
cristalli ionici, e caratterizzati da una
ordinata  disposizione
di ioni positivi e negativi nello spazio. Il cloruro di sodio si presenta
infatti sotto forma di grossi granuli biancastri, ognuno dei quali è considerato
come una macromolecola, costituita da una cella cubica che si ripete
all'infinito nelle tre direzioni dello spazio, con ioni diversi su due vertici
contigui. In questo modo, ogni ione cloro è circondato da
sei ioni sodio e ogni ione sodio è circondato da
sei ioni cloro nelle tre direzioni x, y e
z. Perciò gli ioni sono reciprocamente imbrigliati dall'azione
elettrostatica, e quindi incastonati nel cristallo, per cui non possono muoversi
dal loro posto, ma al massimo vibrare intorno alla posizione di equilibrio.
Siccome il cristallo è fatto di piani sovrapposti, da qualunque parte lo si
guardi, è possibile spaccare il cristallo lungo superfici
piane. I cristalli ionici poi sono pessimi conduttori di corrente
elettrica, giacché tutti gli elettroni sono vincolati ai rispettivi ioni e non
possono andarsene a zonzo per il solido.
disposizione
di ioni positivi e negativi nello spazio. Il cloruro di sodio si presenta
infatti sotto forma di grossi granuli biancastri, ognuno dei quali è considerato
come una macromolecola, costituita da una cella cubica che si ripete
all'infinito nelle tre direzioni dello spazio, con ioni diversi su due vertici
contigui. In questo modo, ogni ione cloro è circondato da
sei ioni sodio e ogni ione sodio è circondato da
sei ioni cloro nelle tre direzioni x, y e
z. Perciò gli ioni sono reciprocamente imbrigliati dall'azione
elettrostatica, e quindi incastonati nel cristallo, per cui non possono muoversi
dal loro posto, ma al massimo vibrare intorno alla posizione di equilibrio.
Siccome il cristallo è fatto di piani sovrapposti, da qualunque parte lo si
guardi, è possibile spaccare il cristallo lungo superfici
piane. I cristalli ionici poi sono pessimi conduttori di corrente
elettrica, giacché tutti gli elettroni sono vincolati ai rispettivi ioni e non
possono andarsene a zonzo per il solido.
In realtà come si è detto nel § 7.5, un legame non è mai totalmente covalente né totalmente ionico, ma la funzione d'onda elettronica risulta sempre dalla sovrapposizione di una parte covalente e di una parte ionica; come al solito, i moduli quadrati dei coefficienti di queste due porzioni rappresentano le probabilità che gli elettroni si trovino nello stato di legame covalente (in compartecipazione) o di legame ionico (strappati a un atomo e acquistati dall'altro). Quale parametro ci dice se il legame è maggiormente ionico o maggiormente covalente? Questo parametro è l'elettronegatività, della quale abbiamo già parlato in precedenza, e che esprime la capacità di legare gli elettroni a sé da parte degli atomi.
Se infatti due atomi hanno la
stessa elettronegatività, attirano a sé gli elettroni allo stesso modo, e dunque
questi sono condivisi ugualmente dai due nuclei. Si parla allora di
legame covalente omeopolare. Questo è ciò che
accade nella molecola biatomica omonucleare come la
molecola d'idrogeno H2. Se però uno dei due atomi tende a
legare a sé gli elettroni più dell'altro, cioè se è più elettronegativo, il
legame covalente è sbilanciato: non è più vero che i due elettroni sono
condivisi ugualmente dai due atomi. Ad esempio, mettendo in comune gli
orbitali più esterni, i
 due atomi
di idrogeno e cloro che formano la molecola di acido cloridrico (HCl) danno vita a un orbitale molecolare con 8 elettroni, e quindi
particolarmente stabile; però, a differenza della molecola H2,
il cloro possiede una maggior forza di
attrazione
degli elettroni rispetto all'idrogeno, per cui l'orbitale molecolare sarà
asimmetrico, come si vede a sinistra, e gli elettroni tenderanno a trovarsi con
maggiore probabilità attorno al primo che attorno al secondo. In questo caso si
parla di legame covalente polare, e la molecola si
trasforma in un dipolo, essendo il cloro
tendenzialmente negativo e l'idrogeno tendenzialmente positivo.
due atomi
di idrogeno e cloro che formano la molecola di acido cloridrico (HCl) danno vita a un orbitale molecolare con 8 elettroni, e quindi
particolarmente stabile; però, a differenza della molecola H2,
il cloro possiede una maggior forza di
attrazione
degli elettroni rispetto all'idrogeno, per cui l'orbitale molecolare sarà
asimmetrico, come si vede a sinistra, e gli elettroni tenderanno a trovarsi con
maggiore probabilità attorno al primo che attorno al secondo. In questo caso si
parla di legame covalente polare, e la molecola si
trasforma in un dipolo, essendo il cloro
tendenzialmente negativo e l'idrogeno tendenzialmente positivo.
Nella tavola periodica, l'elettronegatività aumenta da sinistra verso destra, e dal basso verso l'alto; gli alcalini hanno tendenzialmente i valori più bassi, gli alogeni quelli più alti. Pauling attribuì all'idrogeno un valore di elettronegatività pari a 2,1, al sodio 0,9, al potassio 0,8, al calcio 1,0, al magnesio 1,2, al carbonio 2,5, all'ossigeno 3,5, al bromo 2,9, al cloro 3,0, al fluoro 4,0. Nel caso della molecola di metano, la differenza di elettronegatività tra i due atomi C e H è pari a 2,5 – 2,1 = 0,4; della molecola di HCl, la differenza di elettronegatività tra Cl e H è pari a 3,0 – 2,1 = 0,9; nella molecola dell'acqua (H2O) quella tra O e H è pari a 3,5 – 2,1 = 1,4.; nel caso del cloruro di sodio tra Cl e Na si arriva addirittura a 3,0 – 0,9 = 2,1. Ne consegue che il legame covalente C – H del metano si può considerare omeopolare, ed infatti l'esperienza del getto d'acqua deflesso dalla bacchetta di vetro elettrizzata non sarebbe riproducibile con del metano liquido. Invece, è evidente che la molecola d'acqua presenta una forte polarità, e ciò ha conseguenze macroscopiche. Se il legame covalente è polare, le molecole si comportano come tanti dipoli che si attraggono fra di loro, favorendo la creazione di legami intermolecolari (o legami secondari), e quindi separare tra di loro le molecole, ad esempio facendo bollire il composto, è più difficile. Invece, le molecole prive di polarità non hanno questa possibilità di formare ulteriore forti legami tra di esse, e danno vita a sostanze a bassa temperatura di ebollizione, come la maggior parte dei gas a temperatura ambiente (l'ossigeno bolle a – 183°C, l'azoto a – 196°C, l'idrogeno a – 253°C). Ma su questo torneremo.
Invece, se la differenza di elettronegatività tra i due atomi supera un certo limite, dell'ordine di 1,7 – 2,0, allora l'atomo più elettronegativo strappa letteralmente elettroni all'atomo più elettropositivo, e si formano due ioni, i quali si legano tra di loro per via dell'attrazione coulombiana. Quindi si forma non il legame covalente, ma il legame ionico. Al crescere della differenza di elettronegatività tra gli atomi del legame, si passa dunque dal legame covalente apolare a quello polare al legame ionico, come mostra questa tabella:
|
| Δx | |
Tipo di legame |
Esempio |
|
0 – 0,4 |
Covalente omeopolare |
H–H in H2 |
|
0,4 – 0,8 |
Covalente polare debole |
H–Br in HBr |
|
0,8 – 1,2 |
Covalente polare medio |
H–Cl in HCl |
|
1,2 – 1,8 |
Covalente polare forte |
H–O in H2O |
|
1,8 – 2,0 |
Quasi ionico |
N–H in NH3 |
|
2,0 – 2,2 |
Ionico debole |
Na–Cl in NaCl |
|
2,2 – 2,4 |
Ionico medio |
K–Cl in KCl |
|
2,4 – 3,2 |
Ionico forte |
Na–F in NaF |
Siccome si possono distinguere chiaramente i due tipi di legame solo per valori estremi di | Δx |, nella maggior parte dei casi c'è una frazione di legame covalente e una di legame ionico; è possibile determinare tali frazioni in modo approssimato. Quella di legame covalente è data da:
Se xA = xB, P = 1 e il legame è covalente puro. Se xA >> xB o xA << xB, si ha e–∞ = 0 e il legame è ionico puro. Nell'acido cloridrico (HCl) si ha xH = 2,1 e xCl = 3,0, dunque si ricava facilmente P ≈ 20 %. Nel cloruro di potassio KCl (il celebre antigelo sparso sulle strade), xK = 0,8 e xCl = 3,0, per cui P ≈ 70 %.
È bene però ricordare che questo criterio vale fondamentalmente per molecole biatomiche. Per molecole poliatomiche, l'interazione tra diversi atomi rende troppo difficile poter stabilire la distribuzione degli elettroni di legame tra i diversi atomi solo in base all'elettronegatività di Pauling. Anzi, lo stesso atomo viene ad avere elettronegatività diverse in molecole diverse! Così il carbonio avrebbe elettronegatività 2,5 nel metano (CH4), ma 3,0 nel cloroformio (Cl3CH) e 3,3 nel trifluorometano (CF3H). Infatti, tutte queste molecole hanno quattro atomi oltre ad uno di carbonio, ma tre di fluoro sono più elettronegativi di tre di cloro, e questi di tre di idrogeno, cosicché essi addensano più carica negativa, e di conseguenza il carbonio si fa più elettronegativo!
Si è parlato di cristalli ionici, ma bisogna sottolineare il fatto che esistono anche dei cristalli covalenti. Un esempio per tutti: il diamante. Come si possono realizzare tali cristalli? Abbiamo già visto che l'esistenza di particolari legami covalenti, come quelle di metano, etilene o acetilene, è spiegabile solo per mezzo dell'ibridizzazione degli orbitali atomici. Ora, se ibridiamo gli orbitali più esterni, cioè uno di tipo s e tre di tipo p, ho al massimo un'ibridizzazione di tipo sp3, cioè quattro orbitali con la stessa forma ed energia, distribuiti uniformemente nello spazio, come mostra questo schizzo:

Ciò significa che si formeranno al massimo quattro legami, ovvero che la massima valenza è quattro. Valenza o numero di ossidazione, ricordiamolo, è il numero di legami che ogni atomo può realizzare. Siccome il Primo e il Secondo Periodo della Tavola Periodica sono costituiti da atomi che non vanno al di là della shell L, è evidente che io posso ibridizzare solo orbitali s e p, in base al ragionamento ora compiuto. Nel metano, ad esempio, il carbonio realizza la sua massima valenza, che è quattro. Ma se passiamo ad atomi del Terzo Periodo, essi dispongono anche dell'orbitale d, quindi saranno possibili anche ibridizzazioni di ordine superiore. Il fosforo nelle molecole di PCl5 riesce a costruire gli orbitali ibridi dsp3, unendo agli orbitali 3s e 3p anche un orbitale di tipo 3d. Essi sono in tutto cinque orbitali, disposti nello spazio come si vede qui sotto a sinistra, cioè il fosforo è al centro della base di due piramidi triangolari sovrapposte. Il fosforo, dunque, può esprimere anche valenza cinque! Lo zolfo, poi, arriva ad esprimere valenza sei nelle molecole di SF6, grazie ad un'ibridizzazione di tipo d2sp3, coinvolgendo ben due orbitali 3d, e la forma spaziale è quella di un ottaedro regolare (vedi figura sottostante a destra).

Queste molecole sono possibili per via della scarsa differenza energetica tra gli orbitali 3s, 3p e 3d; infatti, com'è intuitivo comprendere, è impossibile ibridizzare orbitali troppo diversi energeticamente tra di loro. Ciò spiega perchè la massima valenza degli atomi del Terzo Periodo (e successivi) è sette. Un altro aspetto della chimica macroscopica è stato spiegato con i fondamenti della Fisica Microscopica!
Si osserva che, in tutti e cinque i casi di ibridizzazione finora studiati, gli orbitali ibridi risultano uniformemente distribuiti nello spazio. Questo è evidente nella seguente tabella:
|
Molecola |
Ibridizzazione |
Forma |
Struttura |
|
CO2 |
sp |
|
un angolo di 180° |
|
BF3 |
sp2 |
|
tre angoli di 120° |
|
CH4 |
sp3 |
|
sei angoli di 109° |
|
PCl5 |
dsp3 |
|
tre angoli si 120°
e |
|
SF6 |
d2sp3 |
|
dodici angoli di
90° |
Distribuzione uniforme nello spazio degli orbitali ibridizzati
Come si può verificare, i legami si allontanano al massimo l'uno dall'altro, per quanto la geometria lo consente. Si parla in proposito di criterio del massimo allontanamento uniforme: la Natura cerca spontaneamente distribuzioni regolari di questo tipo, perchè rendono minima l'energia. Ma ci torneremo su.
Questo criterio è comunque
rispettato anche dal diamante. Supponiamo
che ad ogni vertice della molecola di metano si leghino al carbonio centrale non
quattro idrogeni, ma altri quattro atomi di carbonio.
Ognuno di essi ha ancora tre legami liberi, per cui
può legare altri tre atomi di carbonio, ed ognuno altri tre... Siccome vale il
criterio del massimo allontanamento uniforme, questi legami devono
 essere
tutti separati da quattro angoli di 109°. Ne consegue una
struttura regolare che si ripete sempre uguale a se stessa,
esattamente come nel cristallo ionico di cloruro di
sodio (vedi modello a destra). La differenza sta nel fatto che ora gli atomi
del reticolo sono tutti uguali, e quindi (Δx = 0) il legame
tra di essi non è ionico, bensì covalente omeopolare.
Come conseguenza, mentre il cristallo ionici di NaCl viene tenuto assieme
da legami elettrostatici, e per questo non direzionati
(il campo elettromagnetico agisce indifferentemente in tutte le direzioni), il
cristallo di carbonio così costruito è caratterizzato da legami
fortemente direzionati. Non sopportano perciò
modifiche imposte da azioni meccaniche: se se ne sollecita la struttura, i
legami si rompono. Dunque questi, che sono detti legami covalenti, sono
molto duri ed estremamente fragili. Il diamante
infatti è in cima alla scala delle durezze di Mohs,
ideata nel 1812 dal mineralogista tedesco Friedrich Mohs
(1773-1839); se lo colpisco adeguatamente, posso romperlo secondo particolari
piani (si parla di "tagliatura" del diamante),
perchè tutti i legami interessati dalla direzione del colpo si spezzano
bruscamente. Durezza e fragilità non sono affatto in contraddizione fra di loro;
anzi, vanno sempre di pari passo! Infatti, se un materiale è
tenero, è anche lavorabile,
perchè posso deformarlo a poco a poco tramite azioni meccaniche. Man mano che il
corpo diventa duro, i suoi legami interatomici si irrigidiscono, e non si può
lavorare: alla minima sollecitazione, anziché scorrere l'uno sull'altro i legami
si rompono , ed esso va in frantumi. E ne riparleremo nel
capitolo seguente a proposito del legame metallico.
essere
tutti separati da quattro angoli di 109°. Ne consegue una
struttura regolare che si ripete sempre uguale a se stessa,
esattamente come nel cristallo ionico di cloruro di
sodio (vedi modello a destra). La differenza sta nel fatto che ora gli atomi
del reticolo sono tutti uguali, e quindi (Δx = 0) il legame
tra di essi non è ionico, bensì covalente omeopolare.
Come conseguenza, mentre il cristallo ionici di NaCl viene tenuto assieme
da legami elettrostatici, e per questo non direzionati
(il campo elettromagnetico agisce indifferentemente in tutte le direzioni), il
cristallo di carbonio così costruito è caratterizzato da legami
fortemente direzionati. Non sopportano perciò
modifiche imposte da azioni meccaniche: se se ne sollecita la struttura, i
legami si rompono. Dunque questi, che sono detti legami covalenti, sono
molto duri ed estremamente fragili. Il diamante
infatti è in cima alla scala delle durezze di Mohs,
ideata nel 1812 dal mineralogista tedesco Friedrich Mohs
(1773-1839); se lo colpisco adeguatamente, posso romperlo secondo particolari
piani (si parla di "tagliatura" del diamante),
perchè tutti i legami interessati dalla direzione del colpo si spezzano
bruscamente. Durezza e fragilità non sono affatto in contraddizione fra di loro;
anzi, vanno sempre di pari passo! Infatti, se un materiale è
tenero, è anche lavorabile,
perchè posso deformarlo a poco a poco tramite azioni meccaniche. Man mano che il
corpo diventa duro, i suoi legami interatomici si irrigidiscono, e non si può
lavorare: alla minima sollecitazione, anziché scorrere l'uno sull'altro i legami
si rompono , ed esso va in frantumi. E ne riparleremo nel
capitolo seguente a proposito del legame metallico.
Riassumendo, nello stato solido della materia le particelle costituenti la materia (molecole, atomi o ioni), a causa delle notevoli forze attrattive e repulsive che esercitano, sono costrette a rimanere localizzate in una struttura spaziale ben definita, detta la struttura cristallina. Di conseguenza, i solidi presentano una proprietà macroscopica caratteristica: sono rigidi e non comprimibili, possedendo volume e forma propria. Alcuni solidi, come il vetro o lo zolfo, derivano dalla rapidissima solidificazione di un fluido, e non presentano alcuna struttura cristallina; vengono perciò detti amorfi o falsi solidi. Il reticolo cristallino si ottiene ripetendo innumerevoli volte nello spazio una cella elementare senza lasciare spazi vuoti. Ad esempio, tagliando un cristallo di calcite (CaCO3) lungo piani determinati, i frammenti che si ottengono presentano la stessa forma del cristallo di origine, evidenziando a livello macroscopico l'esistenza della cella elementare.
A proposito, quello che vedete qui sotto è l'Atomium, costruzione in acciaio che si trova nel Parco Heysel di Bruxelles, alta 102 metri e realizzata in occasione dell'Esposizione Universale del 1958. Contrariamente a quanto credono molti, visto il nome, essa non rappresenta la struttura di un singolo atomo, bensì i nove atomi di una cella unitaria di un cristallo di ferro! Progettato dall'architetto belga André Waterkeyn (1917-2005), in origine sarebbe dovuto durare sei mesi e poi essere smantellato, ed invece, come la Tour Eiffel per Parigi, è diventato uno dei simboli della città! Le sfere, che hanno un diametro di 18 metri, sono collegate da scale dalle quali, tramite finestrature e oblò, è possibile guardare le altre sfere o il panorama sottostante. Tre delle sfere superiori non hanno alcun supporto verticale e quindi, per motivi di sicurezza, non sono aperte al pubblico. Dalle finestre della sfera superiore però si può godere di una vista panoramica di Bruxelles, mentre le altre sfere ospitano diverse mostre. Sembrerebbe incredibile che una città dedichi un monumento a una struttura cristallina, e invece è accaduto!

La scienza che studia la struttura spaziale dei cristalli prende il nome di cristallografia. Le possibili disposizioni di punti nello spazio per formare celle elementari di una struttura cristallina tridimensionale sono quattordici, e prendono il nome di reticoli di Bravais, dal nome del francese Auguste Bravais (1811-1863) che per primo le descrisse nel 1848. I reticoli di Bravais si classificano in base alla forma della cella elementare, a ciascuna delle quali corrisponde uno dei sette sistemi cristallini: cubico, tetragonale, ortorombico, monoclino, triclino, esagonale e romboedrico. La struttura geometrica più comune è quella cubica, che a sua volta si può presentare in tre forme: cubica semplice; cubica a facce centrate; cubica a corpo centrato. Nel cristallo cubico semplice o sc (tipici esempi ne sono la pirite e il cloruro di sodio), le particelle si dispongono ai vertici di minuscoli cubi che si ripetono all'infinito. Nel cubico a corpo centrato o bcc vi è una particella anche al centro della cella cubica; tale struttura cristallina è tipica di molti metalli come gli alcalini, il bario, il cromo, il molibdeno e il tungsteno. Nel cubico a facce centrate o fcc vi è una particella anche al centro di ogni faccia, ed è comune in molti metalli come il magnesio, il calcio e il cobalto.

Varie sostanze, cristallizzando in condizioni differenti, possono dare vita a strutture cristalline diverse; questo fenomeno prende il nome di polimorfismo. Un esempio di polimorfismo è rappresentato dal carbonato di calcio (il già citato CaCO3), che si può presentare sotto forma di calcite, con struttura cristallina romboedrica, oppure di aragonite, con struttura rombica, con diversa durezza, densità e proprietà ottiche. Se è un elemento a presentarsi in più forme cristalline, si parla di allotropia, termine introdotto da Jöns Jacob Berzelius (1779-1848). Ad esempio, il ferro esiste in tre forme allotropiche, dette ferro alfa (a temperature inferiori a 910°C) con un reticolo cubico a corpo centrato, ferro gamma (per temperature comprese tra 910°C e 1394 C) con un reticolo cubico a facce centrate, e ferro delta (per temperature comprese tra 1394°C e 1538 C), con un reticolo cubico a corpo centrato, più compatto di quello del ferro alfa. Anche lo zolfo esiste in due forme allotropiche, zolfo alfa (sotto i 96°C) con struttura ortorombica e zolfo beta (tra 96° e 119°C) con struttura monoclina. Celeberrime sono poi le tre forme allotropiche del carbonio: grafite (strati facilmente sfaldabili con i legami covalenti disposti a forma di esagoni regolari), diamante (cristalli tetraedrici) e fullerene (una struttura di 60 atomi di carbonio legati tra loro in una struttura chiusa formata da 20 esagoni e 12 pentagoni, come un pallone da calcio, scoperta nel 1985).
 Ma non è tutto. Abbiamo visto
che non sempre tutti gli orbitali disponibili intervengono nell'ibridizzazione.
A volte, alcuni orbitali restano quello che sarebbero se gli atomi fossero
isolati; è il caso dell'ammoniaca e dell'acqua.
Nel primo caso, i tre atomi di idrogeno formano legame covalente con tre
orbitali parzialmente vuoti dell'azoto, tutti di tipo 2p, mentre
l'orbitale 2s è del tutto occupato, e quindi non può intervenire nel
legame. Tale coppia di elettroni si dice lone pair
("coppia solitaria"). L'acqua ne ha addirittura due
perchè, come si è visto, sono occupati interamente sia 2s che uno dei tre
orbitali 2p. L'esistenza di questa coppia solitaria può apparire di
scarsa importanza; eppure, è proprio questa che spiega l'esistenza di certe
molecole (legame dativo) e di certi aggregati
molecolari (legame idrogeno)!
Ma non è tutto. Abbiamo visto
che non sempre tutti gli orbitali disponibili intervengono nell'ibridizzazione.
A volte, alcuni orbitali restano quello che sarebbero se gli atomi fossero
isolati; è il caso dell'ammoniaca e dell'acqua.
Nel primo caso, i tre atomi di idrogeno formano legame covalente con tre
orbitali parzialmente vuoti dell'azoto, tutti di tipo 2p, mentre
l'orbitale 2s è del tutto occupato, e quindi non può intervenire nel
legame. Tale coppia di elettroni si dice lone pair
("coppia solitaria"). L'acqua ne ha addirittura due
perchè, come si è visto, sono occupati interamente sia 2s che uno dei tre
orbitali 2p. L'esistenza di questa coppia solitaria può apparire di
scarsa importanza; eppure, è proprio questa che spiega l'esistenza di certe
molecole (legame dativo) e di certi aggregati
molecolari (legame idrogeno)!
Si consideri per esempio la molecola di acido solforico (H2SO4). Come si può costruirla? Lo zolfo ha la stessa struttura elettronica esterna dell'ossigeno, dunque anch'essa presenta due orbitali completamente occupati (3s e 3p–1) e due occupati solo parzialmente (3p0 e 3p+1); entrambi possono allore formare orbitali molecolari con due orbitali di tipo p0 di altrettanti atomi di ossigeno (ad esempio il 2p0). Questi avanzano un orbitale semivuoto ciascuno (il 2p+1), che possono completare formando legame con altrettanti atomi di idrogeno. Il risultato è la molecola di H2SO2, ignota alla chimica. Non sembra che ci siano altri orbitali liberi per formare altri legami. E allora?
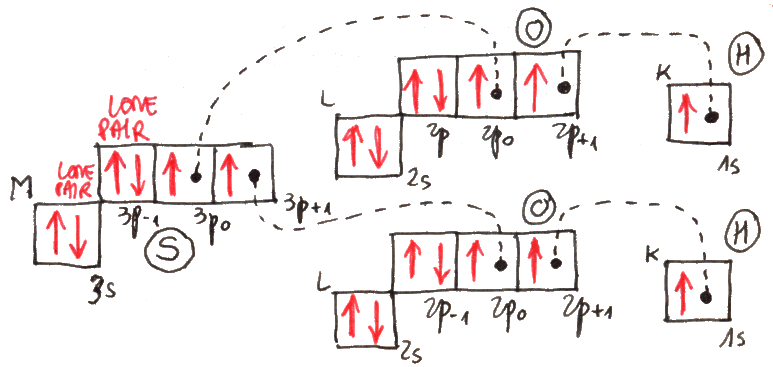
La chiave del rebus sta nell'esistenza dei lone pair 3s e 3p–1 nello zolfo. Infatti, consideriamo l'atomo di ossigeno: per completare l'ottetto, gli mancano due elettroni, e può ottenerli spaiando due elettroni in due orbitali diversi, così da averne due semivuoti, e formando orbitali molecolari come abbiamo appena visto. Ma c'è anche un altro modo per rispettare la regola di Kossel. Infatti l'ossigeno può evitare di spaiare gli elettroni e riempire completamente l'orbitale 2s e due orbitali 2p; il terzo orbitale 2p resta allora tutto vuoto. Se lo zolfo mette in comune tutto intero il suo lone pair con l'ossigeno, riempie l'orbitale mancante e sazia la "fame di elettroni" dell'ossigeno. Si ha così la formazione della molecola di acido solforoso (H2SO3):
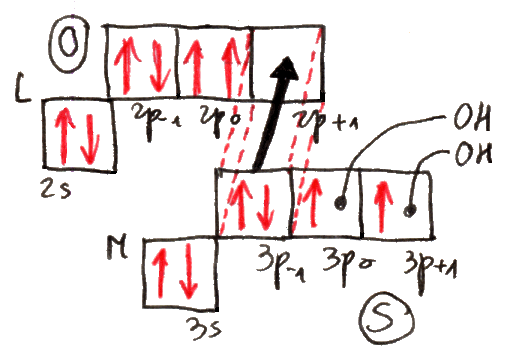
Se poi anche i due elettroni
dell'orbitale 3s dello zolfo vengono messi in società con un altro atomo
di ossigeno, abbiamo proprio la molecola di dell'acido solforico, di cui
qui a destra ho scritto la formula di Lewis e la formula di struttura. La
singolarità di questo legame sta nel fatto che non vengono messi in comune un
elettrone di un atomo uno di un altro, ma due elettroni
appartenenti allo stesso atomo. Si può parlare apertamente di
cessione di una coppia elettronica da un
atomo all'altro, e perciò l'atomo che inizialmente possedeva il lone pair (qui
lo zolfo) si
 dice donatore, quello che la
riceva (qui l'ossigeno) si dice accettore.
Il legame così realizzato si dice legame dativo
o di coordinazione. Il motivo per cui si
forma questo legame è la forte elettronegatività
dell'ossigeno. Esso ha una tale fame di elettroni che, pur di completare
l'ottetto, è disposto ad accettare una lone pair intera. In generale,
l'accettore deve essere più elettronegativo del datore;
e l'accettore è quasi sempre l'ossigeno. Per esercizio, potete provare a
verificare che anche l'anidride solforica (SO3),
l'acido cloroso (HClO2),
l'acido clorico (HClO3) e
l'acido perclorico (HClO4)
si possono costruire solo ricorrendo al legame dativo, a partire dal
monossido di zolfo (SO) e dall'acido
ipocloroso (HClO). Di solito il legame dativo nelle formule di
struttura si indica con una freccia; ma, dopo che
la cessione è avvenuta, non è possibile distinguere l'orbitale molecolare così
ottenuto da quello di un normale legame covalente, cui il legame di
coordinazione assomiglia molto. Anche in esso si può discernere un
frazione elettrostatica, dovuta alla diversa
elettronegatività dei due atomi, ed una covalente,
ma su questo non ci dilungheremo.
dice donatore, quello che la
riceva (qui l'ossigeno) si dice accettore.
Il legame così realizzato si dice legame dativo
o di coordinazione. Il motivo per cui si
forma questo legame è la forte elettronegatività
dell'ossigeno. Esso ha una tale fame di elettroni che, pur di completare
l'ottetto, è disposto ad accettare una lone pair intera. In generale,
l'accettore deve essere più elettronegativo del datore;
e l'accettore è quasi sempre l'ossigeno. Per esercizio, potete provare a
verificare che anche l'anidride solforica (SO3),
l'acido cloroso (HClO2),
l'acido clorico (HClO3) e
l'acido perclorico (HClO4)
si possono costruire solo ricorrendo al legame dativo, a partire dal
monossido di zolfo (SO) e dall'acido
ipocloroso (HClO). Di solito il legame dativo nelle formule di
struttura si indica con una freccia; ma, dopo che
la cessione è avvenuta, non è possibile distinguere l'orbitale molecolare così
ottenuto da quello di un normale legame covalente, cui il legame di
coordinazione assomiglia molto. Anche in esso si può discernere un
frazione elettrostatica, dovuta alla diversa
elettronegatività dei due atomi, ed una covalente,
ma su questo non ci dilungheremo.
Aggiungiamo però almeno due parole sui materiali amorfi (resine, polimeri, vetro, ceramica...). Essi vengono sintetizzati generalmente a partire dallo stato liquido, attraverso un processo di raffreddamento del sistema che ne evita la cristallizzazione: viene mantenuta la tipica struttura microscopica disordinata del liquido, ma portandolo ai livelli di viscosità elevatissimi tipici di un solido. Prendiamo ad esempio il vetro: tipicamente amorfo, è uno dei primi materiali artificiali creati dall'uomo, forse scoperto come sottoprodotto della lavorazione dei metalli. Le qualità che associamo al vetro sono trasparenza, rigidità e fragilità, e nessuno, tranne un fisico, pensa che il vetro non sia un solido. Per i fisici di professione, invece, la questione è molto più complicata. Consideriamo un materiale che certamente non è un vetro, per esempio l'acqua. Quest'ultima a pressione ambiente rimane liquida tra 0° e 100°C, ma non appena abbassiamo la temperatura sotto lo zero diventa ghiaccio. Al punto di fusione, insomma, le proprietà dell'acqua cambiano bruscamente. Nei ruscelli di montagna l'acqua a una temperatura di poco superiore allo zero scorre verso valle proprio come d'estate: l'acqua resta liquida finche non ghiaccia diventando un solido piuttosto duro, così come il ghiaccio non diventa via via più molle prima di squagliarsi. Insomma, tutti suddividiamo i materiali in solidi, liquidi e gassosi e sappiamo che passano da una fase all'altra in maniera istantanea quando si giunge alla temperatura di transizione di fase, ma in realtà siamo circondati da materiali che si comportano in maniera diversa, e il vetro è uno di questi.
Pensiamo a una
candela accesa. Vicino alla fiamma la
cera e un liquido perfetto che, se si rovescia la
candela, cola senza problemi; quando pero comincia a scivolare giù lungo il
bordo della candela, via via che scende si raffredda e cola sempre più
lentamente fino al momento in cui "si blocca" perché la forza di gravità non ce
la fa più a farla scendere. Se interveniamo noi cercando di schiacciarla
(possibilmente non con le dita, per non scottarci), sentiamo che è assai
cedevole e cambia forma senza la necessità di
compiere grandi sforzi. Progressivamente però diventa sempre meno cedevole fino
al punto in cui è a tutti gli effetti un solido. Ma se la cera prima era un
liquido e poi è diventata un solido, quando e a quale temperatura è avvenuto il
passaggio di stato? Difficile rispondere. Possiamo convenzionalmente introdurre
una soglia di durezza e affermare che la cera
diventa solida quando oltrepassa quella soglia, ma la temperatura precisa
dipende dalla soglia scelta. In questa situazione la cera è un
liquido sottoraffreddato, e sotto una certa
temperatura è un solido a tutti gli effetti e diventa quello che i fisici
chiamano vetro. Lo stesso comportamento avviene per
quello che noi chiamiamo comunemente con questa parola: da liquido quasi
perfetto diventa un liquido viscoso e malleabile, un attimo fuggente (per dirla
con l'omonimo film) durante il quale l'artigiano di Murano ne approfitta per
realizzare le sue opere d'arte, ma anche in questo caso non si può individuare
l'istante preciso in cui esso passa da liquido a solido. In pratica,
i materiali amorfi sono metastabili, ovvero si trovano in uno stato
intermedio tra il
 liquido e il solido, e sono
soggetti a lenti cambiamenti strutturali, tali che nell'arco di milioni di anni
essi compiono una vera e propria evoluzione verso configurazioni più stabili. A
lungo è circolata la leggenda (eh sì, anche la Fisica ha le sue leggende!)
secondo cui le vetrate delle antiche cattedrali gotiche,
risalenti al Medioevo, risultano essere più spesse sul
fondo che in cima, e questo dimostrerebbe senza ombra di dubbio che il
vetro è un liquido che scorre molto lentamente. In realtà si tratta solo di una
leggenda metropolitana: non c'è mai stato uno studio scientifico in grado di
dimostrare che quelle antiche vetrate sono più spesse nella parte inferiore; ma,
anche se si rilevassero anomalie, la differenza di spessore non avrebbe nulla a
che vedere con il fatto che il vetro sia un solido o un liquido, bensì sarebbe
dovuta al fatto che il processo di lavorazione del vetro che veniva utilizzato
all'epoca non era in grado di produrre lastre perfette con spessore uniforme.
Conclusione: il vetro è un solido, anche se qualcuno preferisce l'espressione
"falso solido", essendo privo di struttura
cristallina.
liquido e il solido, e sono
soggetti a lenti cambiamenti strutturali, tali che nell'arco di milioni di anni
essi compiono una vera e propria evoluzione verso configurazioni più stabili. A
lungo è circolata la leggenda (eh sì, anche la Fisica ha le sue leggende!)
secondo cui le vetrate delle antiche cattedrali gotiche,
risalenti al Medioevo, risultano essere più spesse sul
fondo che in cima, e questo dimostrerebbe senza ombra di dubbio che il
vetro è un liquido che scorre molto lentamente. In realtà si tratta solo di una
leggenda metropolitana: non c'è mai stato uno studio scientifico in grado di
dimostrare che quelle antiche vetrate sono più spesse nella parte inferiore; ma,
anche se si rilevassero anomalie, la differenza di spessore non avrebbe nulla a
che vedere con il fatto che il vetro sia un solido o un liquido, bensì sarebbe
dovuta al fatto che il processo di lavorazione del vetro che veniva utilizzato
all'epoca non era in grado di produrre lastre perfette con spessore uniforme.
Conclusione: il vetro è un solido, anche se qualcuno preferisce l'espressione
"falso solido", essendo privo di struttura
cristallina.
Non è facile elaborare una teoria microscopica convincente che spieghi le proprietà caratteristiche del vetro e in generale dei materiali amorfi; sono state fatte varie proposte alternative, ma nessuna per ora risolutiva. Un passo avanti importante è stato fatto nel 2018 da Tullio Scopigno del Dipartimento di Fisica della Sapienza di Roma, il quale ha scoperto quali sono gli effetti dell'invecchiamento sulle proprietà elastiche di una resina amorfa utilizzando un fossile di ambra vecchio di 110 milioni di anni, proveniente dal giacimento di El Soplao in Cantabria. La diretta osservazione dell'evoluzione delle proprietà dei materiali amorfi presenta infatti una difficoltà pratica non indifferente: essa avviene su scale temporali estremamente lente, inaccessibili all'osservazione sperimentale. Per osservare sperimentalmente gli effetti dell'invecchiamento sulle proprietà di un sistema amorfo entro un arco temporale geologico di milioni di anni, Scopigno ha riscaldato l'ambra (che altro non è se non resina di alberi fossilizzata) per un certo tempo al di sopra della sua temperatura di transizione vetrosa, e poi raffreddata alla temperatura ambiente seguendo la convenzionale procedura di vetrificazione. In questo modo il fossile è stato riportato allo stato in cui era quando si è formato per la prima volta: una sorta di "lifting" termico per cancellare le tracce del tempo e ottenere un ringiovanimento di 110 milioni di anni. Il confronto delle proprietà dell'ambra prima e dopo il ringiovanimento termico ha permesso di collegare per la prima volta, quantificandolo, il grado di disordine di un materiale amorfo alla sua età, rivelando in che modo le proprietà elastiche del materiale sono evolute durante il processo di stabilizzazione.
Questi studi sono molto importanti, perché i materiali amorfi sono più importanti di quanto si pensi. Molti farmaci, per esempio, sono sintetizzabili solo in forma amorfa perchè la forma cristallina, quando esiste, ha un minor grado di solubilità. La tendenza alla cristallizzazione determina la data di scadenza di un farmaco: ecco perché capire i meccanismi di stabilizzazione di un materiale amorfo è un aspetto di grande interesse per l'industria farmaceutica. In un campo diverso, quello dell'ottica, ci sono almeno tre applicazioni che hanno rivoluzionato la nostra percezione del mondo, tutte basate sull'indice di rifrazione del vetro: il microscopio, lo strumento che ha permesso le più importanti scoperte in biologia; il telescopio, tramite cui è stata dimostrata la veridicità del modello eliocentrico; le fibre ottiche, che hanno radicalmente modificato i nostri standard di comunicazione con un impatto incalcolabile sullo sviluppo sociale ed economico mondiale. I margini di sviluppo tecnologico per i materiali amorfi nel settore dell'ottica sono ancora largamente inesplorati, dall'ingegnerizzazione delle superfici vetrose per indurre proprietà idrofobiche, oleofobiche, antiriflesso, eliminando la necessità di trattamenti esterni soggetti a deterioramento, fino alla sintesi di nuovi materiali con bassa attenuazione, fondamentali nel campo della fotonica (laser al femtosecondo e dispositivi optoelettronici). Ma la rilevanza dei materiali vetrosi non e limitata alle grandi scoperte scientifiche, dato che le applicazioni includono tecnologie largamente diffuse nella nostra vita quotidiana: basti pensare al Gorilla Glass, ormai comunemente usato negli smartphone per la sua resistenza. In questo campo il futuro della ricerca sarà sempre più orientato alla frattografia, lo studio delle caratteristiche delle fratture per risalire alle cause che le generano tramite esperimenti, modellizzazioni teoriche e simulazioni al computer. C'e poi l'ampia classe dei metalli amorfi, modellabili controllandone la viscosità che, nella fase di liquido sottoraffreddato, varia in modo continuo in un ampio intervallo di temperatura. L'assenza di difetti reticolari conferisce a questi materiali maggiore resistenza rispetto alla controparte cristallina, rendendoli particolarmente adatti per applicazioni biomediche o nel campo delle attrezzature sportive. Il futuro della ricerca in questo campo e riuscire a combinare durezza e rigidità del vetro alla resistenza del metallo, senza la fragilità e la malleabilità, gli svantaggi che caratterizzano rispettivamente le due tipologie di materiale.
.
7.9 Perchè l'acqua e l'argo congelano?
Quelli di cui abbiamo parlato finora sono i cosiddetti legami chimici primari, cioè quelli che portano alla formazione di aggregati di atomi, e precisamente molecole, cristalli covalenti, cristalli ionici, legami di coordinazione. Mancano all'appello i cristalli metallici, dovuti al cosiddetto legame metallico, cui però dedicheremo il capitolo successivo, perchè si tratta di qualcosa di fondamentalmente diverso. Vogliamo invece accennare in quest'ultimo paragrafo ai legami chimici secondari, cioè a quelli che portano alla formazione di aggregati di molecole: siamo dunque ad un secondo livello di aggregazione.
Chiediamoci: esistono legami tra le diverse molecole? Certamente. Infatti i solidi e i liquidi si comportano come un tutt'uno proprio perché i loro costituenti fondamentali si aggregano in qualche modo tra di loro. Esistono dei solidi covalenti, ionici e metallici, formati da atomi singoli legati reciprocamente, e che si comportano come enormi molecole; ma esistono anche dei solidi molecolari, formati da aggregati di molecole, così come una casa è fatta di mattoni cementati assieme. Caso tipico di questi solidi è il ghiaccio d'acqua, nel quale le molecole di H2O sono strettamente aderenti le une alle altre e disposte ordinatamente nello spazio. Non possiamo supporre che tra queste molecole si realizzino legami né di tipo covalente né di tipo dativo, perché gli orbitali sono tutti saturi, e non c'è più neanche un elettrone a disposizione. E allora?
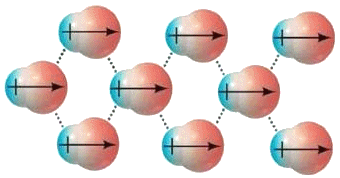 Ricordiamoci
che, nelle molecole d'acqua, ossigeno e idrogeno sono legati tra di loro da un
legame covalente polare, perchè l'ossigeno lega a
sé gli elettroni più dell'idrogeno. La molecola d'acqua dunque si comporta
stabilmente come un dipolo elettrico, e e i dipoli
elettrici si attraggono tra di loro. Il legame è
piuttosto debole: bastano poche decine di kiloJoule
per mole di sostanza per romperlo. Ciò spiega perchè i solidi molecolari,
costruiti su questo principio, hanno un basso punto di
fusione: mentre il ferro (solido metallico) fonde a 1535° e il
cloruro di sodio (solido ionico) fonde ad 808°, il ghiaccio d'acqua fonde
già a 0°C. Inoltre, se sottoposti ad azioni
meccaniche, questi solidi non si rompono in modo geometricamente
determinato, come il diamante e i cristalli ionici, ma
vanno in frammenti, come quando si prende a martellate un blocco di
ghiaccio per metterlo nel cestello dello champagne. Si osservi che la coesione
di questi solidi molecolari aumenta con la polarità della
molecola: la differenza di elettronegatività tra azoto e idrogeno è
minore di quella tra ossigeno ed idrogeno, e di conseguenza la molecola di
ammoniaca (NH3)
è molto meno polare di quella d'acqua. Non è un caso se il suo stato solido
fonde già a – 77°C.
Ricordiamoci
che, nelle molecole d'acqua, ossigeno e idrogeno sono legati tra di loro da un
legame covalente polare, perchè l'ossigeno lega a
sé gli elettroni più dell'idrogeno. La molecola d'acqua dunque si comporta
stabilmente come un dipolo elettrico, e e i dipoli
elettrici si attraggono tra di loro. Il legame è
piuttosto debole: bastano poche decine di kiloJoule
per mole di sostanza per romperlo. Ciò spiega perchè i solidi molecolari,
costruiti su questo principio, hanno un basso punto di
fusione: mentre il ferro (solido metallico) fonde a 1535° e il
cloruro di sodio (solido ionico) fonde ad 808°, il ghiaccio d'acqua fonde
già a 0°C. Inoltre, se sottoposti ad azioni
meccaniche, questi solidi non si rompono in modo geometricamente
determinato, come il diamante e i cristalli ionici, ma
vanno in frammenti, come quando si prende a martellate un blocco di
ghiaccio per metterlo nel cestello dello champagne. Si osservi che la coesione
di questi solidi molecolari aumenta con la polarità della
molecola: la differenza di elettronegatività tra azoto e idrogeno è
minore di quella tra ossigeno ed idrogeno, e di conseguenza la molecola di
ammoniaca (NH3)
è molto meno polare di quella d'acqua. Non è un caso se il suo stato solido
fonde già a – 77°C.
Il legame che dà vita a questi solidi molecolari è dunque di natura elettrostatica, non coinvolge la messa in comune di elettroni, e prende il nome di legame dipolo-dipolo. Ad esso si deve la nostra possibilità di sorbirci una granita o di farci una sciata in montagna. Questo però ci solleva un interrogativo: solo le sostanze costituite da molecole polari possono congelare? Se vi fosse in gioco solo il legame dipolo-dipolo, sarebbe così. Ma c'è un dato di fatto che ci mette in crisi: anche il gas costituito dalla molecola con legame covalente omeopolare per eccellenza, quella di idrogeno (H2), congela, anche se alla bassissima temperatura di – 259,14°C. E non basta: persino i solitari gas nobili, che si accontentano della molecola monoatomica, solidificano: l'argo diventa solido a – 189,2°C. Una cosa è certa: a tenere insieme le molecole di queste sostanze in un solido non è né il legame covalente, né quello dipolo-dipolo. L'argo non forma legami neppure in una molecola, figuriamoci in un solido, e i suoi orbitali, come sappiamo, sono tutti perfettamente simmetrici o antisimmetrici rispetto alle coordinate spaziali: niente dipolo permanente, dunque.
 Tuttavia lo scienziato
olandese Johannes Diderik van der Waals
(1837-1923), Premio Nobel nel 1910, ebbe un'idea geniale.
È vero che l'atomo di argo non presenta
polarità permanente, però è polarizzabile. Infatti
il moto degli elettroni è in realtà fluttuante:
come ormai sappiamo, essi non descrivono affatto un'orbita ben precisa, ma
esiste una regione di spazio in cui è probabile trovarli. Ma chi ci dice che
l'elettrone si muove attorno al nucleo in modo che il baricentro della sua
distribuzione di carica negativa coincida con quello della carica positiva, cioè
con il nucleo? In realtà, sono possibili delle
fluttuazioni. Tutti gli atomi vanno soggetti, nella materia, a moti di
vibrazione e di rotazione, e quindi è probabile che, in certi istanti,
l'elettrone si trovi più frequentemente da una parte dell'atomo che dalla parte
opposta. Ora, se ad un certo istante la molecola omeopolare (o l'atomo, come nel
caso dei gas nobili) si viene a trovare con un momento di
dipolo fluttuante, cioè con la carica negativa più addensata da una parte
che dall'altra della molecola, questo può indurre un analogo momento di dipolo
nelle molecole adiacenti; si formano così dei dipoli
fluttuanti, che si attraggono reciprocamente. Beninteso, dopo poche
frazioni di secondo il dipolo fluttuante verrà meno, ma si costituirà di nuovo
in un'altra direzione per via delle continue oscillazioni elettroniche, e si
ricostituirà un esile legame con gli atomi o le molecole vicine per via
dell'induzione elettrostatica. Si parla di forze di
dispersione, per indicare la mutua attrazione tra i dipoli indotti
dalle fluttuazioni, perchè il legame si disperde e si ricostituisce in
continuazione, o anche di forze di London,
dal nome del chimico tedesco Wolfgang Fritz London
(1900-1954). Il legame che così si viene a formare è detto
legame di van der Waals.
Tuttavia lo scienziato
olandese Johannes Diderik van der Waals
(1837-1923), Premio Nobel nel 1910, ebbe un'idea geniale.
È vero che l'atomo di argo non presenta
polarità permanente, però è polarizzabile. Infatti
il moto degli elettroni è in realtà fluttuante:
come ormai sappiamo, essi non descrivono affatto un'orbita ben precisa, ma
esiste una regione di spazio in cui è probabile trovarli. Ma chi ci dice che
l'elettrone si muove attorno al nucleo in modo che il baricentro della sua
distribuzione di carica negativa coincida con quello della carica positiva, cioè
con il nucleo? In realtà, sono possibili delle
fluttuazioni. Tutti gli atomi vanno soggetti, nella materia, a moti di
vibrazione e di rotazione, e quindi è probabile che, in certi istanti,
l'elettrone si trovi più frequentemente da una parte dell'atomo che dalla parte
opposta. Ora, se ad un certo istante la molecola omeopolare (o l'atomo, come nel
caso dei gas nobili) si viene a trovare con un momento di
dipolo fluttuante, cioè con la carica negativa più addensata da una parte
che dall'altra della molecola, questo può indurre un analogo momento di dipolo
nelle molecole adiacenti; si formano così dei dipoli
fluttuanti, che si attraggono reciprocamente. Beninteso, dopo poche
frazioni di secondo il dipolo fluttuante verrà meno, ma si costituirà di nuovo
in un'altra direzione per via delle continue oscillazioni elettroniche, e si
ricostituirà un esile legame con gli atomi o le molecole vicine per via
dell'induzione elettrostatica. Si parla di forze di
dispersione, per indicare la mutua attrazione tra i dipoli indotti
dalle fluttuazioni, perchè il legame si disperde e si ricostituisce in
continuazione, o anche di forze di London,
dal nome del chimico tedesco Wolfgang Fritz London
(1900-1954). Il legame che così si viene a formare è detto
legame di van der Waals.
Come si intuisce, questo legame è così debole che bastano energie dell'ordine di 1 KJ/mol per distruggerlo. Questo è il motivo per cui i solidi molecolari così ottenuti sussistono sì (cioè l'idrogeno e l'argo possono solidificare), ma solo a bassissime temperature, quelle indicate poco fa. Naturalmente queste temperature sono tanto più alte quanto più facilmente si possono spostare da una parte all'altra gli elettroni di una molecola. Dunque, mentre il legame dipolo-dipolo e i legami primari covalente, ionico e dativo sono governati dall'elettronegatività, il legame di van der Waals è governato dalla polarizzabilità. L'anidride carbonica (CO2) è più polarizzabile dell'argo, quindi solidifica a – 83°C, ma l'argo lo è più dell'idrogeno. In generale, più una molecola è grossa, più è polarizzabile, perchè gli elettroni si spostano maggiormente al suo interno. È il caso degli idrocarburi, come l'esano (C6H14), che bolle a 68,7°C, e l'eptano (C7H16), che bolle a 98,4°, temperature confrontabili a quelle di ebollizione dell'acqua, che al contrario di esse è una molecola fortemente polare.
Facciamo osservare che, in generale, liquidi polari e liquidi non polari risultano immiscibili tra loro, mentre è possibile mescolare liquidi polari diversi o liquidi non polari diversi tra loro. Infatti il legame ione-dipolo si manifesta indifferentemente tra poli positivi e poli negativi di qualsiasi tipo di molecole, purché esse si comportino come dipoli elettrici; e così il legame di van der Waals si manifesta tra dipoli fluttuanti, qualunque sia la loro struttura chimica. Ma, se mescolo un liquido polare ed uno non polare, le molecole polari resteranno unite tra di loro in virtù del legame dipolo-dipolo, e quelle apolari in virtù del legame di van der Waals, e non si mescoleranno mai tra di loro. È per questo motivo che la benzina, costituita da idrocarburi non polari, galleggia sull'acqua senza mischiarsi con essa.
Ma non finisce qui se, oltre alle molecole, entrano in gioco gli ioni. Come abbiamo visto, nel legame ionico la reciproca attrazione elettrostatica tiene uniti ioni di carica diversa. Il legame dipolo-dipolo e quello di van der Waals tengono unite molecole diverse che presentano un momento di dipolo fisso o fluttuante, sempre per via dell'attrazione coulombiana. Non può allora mancare un legame in cui questo tipo di attrazione riunisce ioni e molecole: è il cosiddetto legame ione-dipolo. Se noi prendiamo un solido ionico e lo immergiamo in un liquido opportuno, detto solvente, esso tende a disciogliersi, cioè a perdere la propria integrità. Succede anche a un solido molecolare come una zolletta di zucchero. Però, mentre le singole molecole di glucosio (C6H12O6) si disperdono nell'acqua conservando ciascuna la propria identità chimica, così non accade con un solido ionico come il cloruro di sodio in acqua. Infatti nessuno ignora che l'interazione elettromagnetica si indebolisce in presenza di un dielettrico; il legame ionico in soluzione allora si allenta. Ma il vero motivo per cui il nostro NaCl si scinde in ioni Na+ e Cl– che si disperdono nel solvente, perdendo qualunque proprietà del composto originario, sta nel fatto che ogni ione viene circondato dai dipoli elettrici costituiti dalle molecole d'acqua:
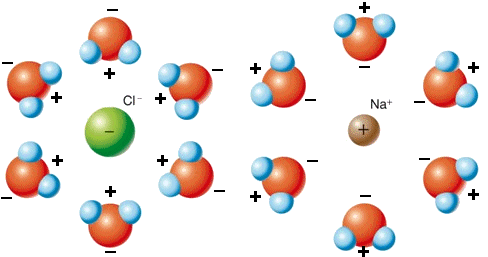
Attorno allo ione Na+ le molecole d'acqua si dispongono rivolgendo verso di esso gli atomi di ossigeno, in cui prevale la carica negativa; lo ione Cl–, è circondato da molecole dalla parte dell'idrogeno, in cui invece prevale la carica positiva. In altre parole, gli ioni Na+ e Cl– si rivestono di molecole d'acqua. Tale fenomeno è detto idratazione e, più in generale, solvatazione, perchè il solvente ricopre rapidamente gli ioni. Questo avviene perchè, come si può dimostrare, l'energia del legame ione-dipolo è minore di quella del legame ione-ione nel solvente. Siccome la Natura cerca sempre di minimizzare l'energia, preferisce sacrificare l'integrità del solido ionico e ricoprire gli ioni d'acqua, e così si spiega perchè i cristalli ionici sono solubili in liquidi polari. Inutile dire che ciò non avviene in liquidi apolari come gli idrocarburi. Il legame ione-dipolo è responsabile della solubilità e delle caratteristiche di certe soluzioni. La soluzione ottenuta sciogliendo cloruro di sodio in acqua è fortemente conduttrice di elettricità, perchè gli ioni negativi o anioni vengono attirati dall'anodo, l'elettrodo positivo, mentre gli ioni positivi o cationi sono attratti dal catodo, l'elettrodo negativo (anodo e catodo in greco significano rispettivamente "strada in salita" e "strada in discesa").
La nostra rassegna sui legami chimici non può chiudersi senza un ceno al cosiddetto legame idrogeno. Anch'esso nasce in conseguenza della forte elettronegatività di certi atomi nei confronti dell'idrogeno. Quando atomi come fluoro, cloro, ossigeno, azoto si trovano legati all'idrogeno, hanno vita molecole di forte polarità, per cui la nube elettronica si sposta verso l'atomo più elettronegativo. L'atomo di idrogeno è così privato della sua copertura elettronica o, come si suol dire, è protonizzato. Esso si comporta allora come la famosa bacchetta di vetro strofinata, in grado di attrarre bacchette di ebanite strofinate a loro volta; può cioè attirare, in virtù della sua carica spiccatamente positiva, gli atomi di altre molecole che con esso formano legame, sui quali è prevalente la carica negativa. Naturalmente, tale legame è caratteristico dell'atomo di idrogeno, da cui il nome; si manifesta tra molecole come l'acqua, l'acido fluoridrico, l'acido cloridrico, l'ammoniaca; e non è un vero e proprio legame, non portando alla formazione di molecole o di aggregati stabili, bensì piuttosto un'interazione, come il legame ione-dipolo, e precisamente di natura elettrostatica. Quest'interazione è la più forte che sia mai stata riscontrata tra molecole differenti, e ciò spiega come mai l'acqua bolla solo a 100°. La molecola omologa di acido solfidrico (H2O), in cui al posto dell'ossigeno c'è il suo parente stretto zolfo, posto sotto di esso nella tavola periodica, bolle molto sotto lo zero centigrado, e precisamente a – 60°C, perchè lo zolfo non è abbastanza elettronegativo da dare vita a legami idrogeno!
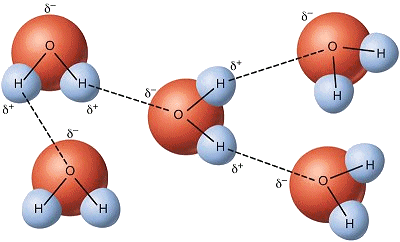
Alcuni autori riconoscono che il legame idrogeno, come quello covalente e quello dativo, è la combinazione lineare di due diverse funzioni d'onda, una delle quali descrive effettivamente l'interazione elettrostatica tra l'idrogeno positivo e il partner negativo, come nel legame dipolo-dipolo, ed una descrive invece il legame come un'effettiva cessione all'idrogeno di un lone pair. Infatti si sa sa che la molecola (specie se molto polare) ha una componente ionica in cui un atomo si prende tutta la carica negativa, e gli altri tutta quella positiva. L'acqua, perciò, può essere descritta come l'interazione tra uno ione ossigeno due volte negativo (O2–) e due ioni idrogeno (H+). Questi ultimi sono completamente denudati, cioè ridotti a due protoni (da cui l'aggettivo "protonizzati"), ed hanno una "fame" incredibile di elettroni; sono perciò disposti ad accogliere un lone pair ciascuno dell'ossigeno di un'altra molecola, come in un legame dativo. Ciò spiega perchè spesso l'idrogeno, l'ossigeno di una stessa molecola e l'idrogeno di una molecola diversa sono allineati, come si dimostra con esperienze di diffrazione. In effetti, questa situazione non è mai evidenziabile in modo diretto, ma il legame idrogeno è una combinazione lineare di questa e di un'altra in cui a prevalere è la semplice attrazione elettrostatica. Questo modello di legame idrogeno fu proposto nel 1920 dai chimici statunitensi Wendell Latimer (1893-1955) e Worth H. Rodebush (1887-1959), ed è sostanzialmente interpretabile come un legame in cui un atomo d'idrogeno lega a sé altri due atomi. Esso è molto più importante di quanto non sembri a prima vista perchè, interessando i legami O–H e N–H, è responsabile della formazione di un gran numero di composti organici, ed in particolare è fondamentale nella struttura delle proteine e del DNA, mattoni base della nostra biologia. È per questo che il legame dativo è detto anche il legame della vita. Del resto, senza di esso l'acqua bollirebbe sotto zero come l'acido solfidrico, e la vita sul nostro pianeta non sarebbe possibile. Se noi stessi viviamo e respiriamo, lo dobbiamo proprio all'apparentemente insignificante legame idrogeno!
Il legame ionico (primario) e i legami dipolo-dipolo, ione-dipolo, idrogeno e di van der Waals (secondari) si dicono legami elettrostatici, mentre il legame covalente, il legame metallico e il legame dativo (primari) si dicono legami di scambio. Si noti come tutti i legami secondari finora analizzati siano di natura elettrostatica; dunque, sia la cosiddetta "forza molecolare" che tiene uniti gli atomi nella molecola, sia la "forza di aggregazione" che tiene unite le molecole tra di loro, ritenute forze fondamentali dai chimici e dai fisici del XIX secolo, sono in realtà casi particolari dell'interazione elettromagnetica.
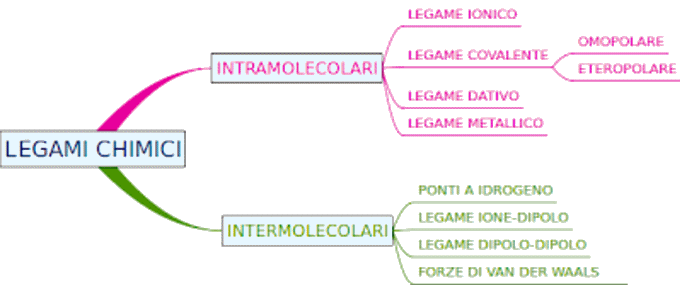
.
Prima di cambiare capitolo, ecco la soluzione del quesito che vi ho proposto sopra circa la configurazione elettronica del ferro: [Ar] 4s2 3d6, quello del gadolinio: [Xe] 6s2 5d1 4f7 e quella del flerovio: [Rn] 7s2 5f14 6d10 7p2. Se ci siete riusciti, mi complimento con voi, perchè avete assimilato perfettamente i contenuti di questo capitolo!
 |
 |
Due divertenti meme
che girano in rete sul
Principio di Esclusione e sulle differenze tra il semplicistico modello atomico
di J.J. Thomson, quello di Bohr e quello difficilissimo ad orbitali. Se avete capito
le battute, questa lezione vi è chiara! :)
.
È ora venuto il momento di approfondire lo studio dell'ultimo tipo di legame che ci manca da analizzare, quello metallico. Ne saprete di più se passerete con me al capitolo seguente; per tornare all'indice, invece, il link è questo.
