Esperienze di Fisica: la rivoluzione di Galileo

	Con questa foto avviamo la meccanica, e non potevamo che cominciare con un busto di Galileo Galilei (1564-1642) conservato nel Museo Galileo di Firenze, dove è stato fotografato dalla mia allieva Sara Scampini (5 G a.s. 2011/12). Lo scienziato pisano è considerato l'ideatore del moderno metodo sperimentale; nei suoi "Discorsi e dimostrazioni matematiche intorno a due nuove scienze attenenti alla meccanica e i movimenti locali" (1638) fondò la Cinematica e la Dinamica, mentre nel suo "Dialogo sopra i due massimi sistemi del mondo" (1632) dimostrò la veridicità del sistema eliocentrico di Copernico contro quello geocentrico di Tolomeo.
	Qui vedete il dispositivo sperimentale adatto per studiare le leggi del moto rettilineo uniforme. Come si vede il trasformatore alimenta il marcatempo elettromagnetico (vedi più sotto), tra i cui rebbi scorre la carta carbone (qui non presente) ancorata al carrellino semovente, a sua volta posto al di sopra dell'apposita guida metallica. I punti lasciati dal marcatempo sulla carta carbone risultano equidistanti. Ecco un filmato di questa esperienza.
	Ed ecco invece il dispositivo sperimentale necessario per la verifica delle leggi del moto rettilineo uniformemente accelerato. Un carrellino non semovente cade lungo un piano inclinato, oppure a trascinarlo è un pesetto che scorre su una carrucola, e la sua velocità in ogni istante è misurata per mezzo di un foglio di carta carbone fissato al carrellino che scorre tra i rebbi di un marcatempo elettromagnetico, descritto subito sotto. Eccovi anche un filmato digitale di questa esperienza.
	Il marcatempo elettromagnetico appena nominato è un geniale accessorio da laboratorio che può utilmente sostituire il comune cronometro. Il suo percussore batte esattamente 50 volte al secondo, e dunque lascia sulla carta carbone in movimento sotto di esso una serie di tracce. Separando le tracce in gruppi di 5, la lunghezza di ciascun gruppo corrisponde dunque allo spazio percorso dalla carta carbone (e dal dispositivo che la trascina) in un decimo di secondo. In tal modo è possibile calcolare velocità ed accelerazione nel moto rettilineo uniforme e nel moto rettilineo uniformemente accelerato.
	Per studiare il moto rettilineo uniforme bisogna fare ricorso ad un carrellino semovente. Lo si aziona mediante l'interruttore posto sulla faccia superiore, può procedere in entrambe le direzioni e la velocità è regolabile da un minimo ad un massimo con l'apposita levetta. Il cilindretto arancione rappresenta il dispositivo di bloccaggio per la striscia di carta carbone che il carrellino si trascinerà dietro, facendolo passare sotto i rebbi del marcatempo (vedi figura precedente). Eseguendo tre prove con velocità minima, intermedia e massima, è facile realizzare i diagrammi orari del moto rettilineo uniforme.
	La fotografia, scattata dai miei alunni di Seconda Liceo Classico, mostra il carrellino non semovente necessario per le suddette esperienze di cinematica. Su di esso è indicata la massa (tara), pari a 50 grammi, e l'asta verticale al centro serve per infilarvi dei pesi, come si vedrà in altre foto successive di questa galleria. A dispetto della sua semplicità, si tratta di un componente piuttosto delicato: se cade in terra si sfascia facilmente, per cui necessita porre un alunno seduto lateralmente rispetto al banco, così da impedire che esso caschi al termine della sua corsa lungo la guida metallica.
	La fotografia di Marta Milano (III B cl. a.s. 2004/2005) mostra l'intero ripiano di cinematica di questo scaffale del nostro Laboratorio Virtuale. In esso si vedono illustrati strumenti d'epoca ma perfettamente funzionanti come una guida metallica, un carrellino semovente ed una leva di primo genere a bracci uguali!
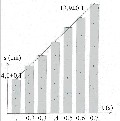
	Lo schema in figura è stato realizzato dal sottoscritto ritagliando i gruppi di cinque puntini lasciati sulla carta carbone dal mio marcatempo elettromagnetico, ed incollandoli verticalmente su di un diagramma cartesiano da me opportunamente approntato. In ascissa vi è dunque il tempo (ogni tratto rappresenta un decimo di secondo), in ordinate la velocità, e non lo spazio, perchè la lunghezza di ogni tratto rappresenta lo spostamento del carrellino nell'unità di tempo!! Come si vede, la velocità cresce linearmente con il tempo, e ciò dimostra che il moto è effettivamente uniformemente accelerato!
	Gli esperimenti di cinematica possono essere eseguiti facendo ricordo ad una guidovia a cuscino d'aria, una guida metallica sulla quale vengono fatti scorrere degli strumenti chiamati cavalieri. La loro posizione e la loro velocità viene registrata tramite un sensore a raggi infrarossi, mentre il tempo viene misurato con un cronometro. Con essa si possono dunque eseguire esperimenti simili a quelli condotti da Galileo Galilei.
	Come fare per simulare il moto rettilineo uniforme? Occorre eliminare l'attrito. A questo scopo si utilizza un accrssorio detto turboventilatore ad aria compressa, in pratica un "aspirapolvere al contrario" che soffia getti di aria dentro la guida; l'aria esce da forellini praticati lungo di essa e mantiene i cavalieri sollevati, così da ridurre l'attrito praticamente a zero. Il moto rettilineo uniformemente accelerato si realizza imprimendo ai cavalieri una spinta con una molla.
	Quella che qui vedete è la riproduzione di un celeberrimo esperimento di Galilei, eseguita nell'ambito di una mostra dedicata a Galileo Galilei nel gennaio 2012 dagli studenti del mio Liceo. Il grande scienziato pisano fece rotolare delle sferette metalliche lungo un piano inclinato, facendole partire da 10, 40, 90, 160 centimetri dalla base del piano, e misurò i tempi impiegati dalle palline contando le gocce d'acqua uscite da un serbatoio durante la discesa (a quei tempi non vi erano cronometri di sorta). Galileo mostrò così che gli spazi percorsi lungo il piano inclinato sono direttamente proporzionali ai quadrati dei tempi necessari per le discese, giusto come previsto dalle leggi del moto rettilineo uniformemente accelerato!
	Combinando un moto rettilineo uniforme orizzontale ed un moto uniformemente accelerato verticale (il moto dei gravi) si ottiene un moto parabolico. L'esempio più chiaro è fornito dai getti d'acqua delle fontane che, come dimostra questa fotografia scattata dall'autore di questo sito, seguono proprio un traiettoria di questo tipo. La dimostrazione che il moto dei proiettili è di tipo parabolico si deve al solito Galileo Galilei.
	La foto a sinistra mostra uno speciale cannoncino in grado di riprodurre in laboratorio il moto parabolico. Basta inserirvi una palla di plastica, tirare la cordicella e una molla lo spara ad una certa distanza lungo una traiettoria chiaramente parabolica. Difficile però effettuare misure di velocità e di gittata, perchè l'attrito dell'aria vanificherebbe ogni tentativo di previsione. Cliccando qui potrete visionare un breve filmato digitale che illustra il moto parabolico della pallina.
	Un'esperienza semplice da realizzare e di sicuro successo: il tubo a vuoto. Si tratta di un tubo dal quale si pompa fuori tutta l'aria mediante l'apposita macchina pneumatica. In esso sono contenuti un piombino ed una piuma. In presenza di aria, capovolgendo il tubo, essi cadono in tempi diversi a causa del forte attrito dell'aria; una volta che quest'ultima è stata aspirata, gli studenti osservano con sorpresa che piombino e piuma cadono insieme verso il basso. Si dimostra così l'assunto di Galileo Galilei secondo il quale il tempo di caduta è indipendente dalla massa dell'oggetto.
	Lo scatto qui accanto rappresenta lo strumento principe per la misura delle forze: il dinamometro. Si tratta di un semplice strumento che applica la legge di Hooke sull'elasticità: le deformazioni della molla sono direttamente proporzionali agli sforzi applicati. Come si vede in questa immagine, il dinamometro in questione è costituito da un cilindro esterno trasparente e da uno interno, nel quale scorre la molla. Quest'ultimo cilindro di colore dorato è tarato direttamente in grammi peso, facilmente leggibili a seconda del numero di taccature che emerge dal bordo inferiore.
	Un semplice dispositivo, ripreso direttamente dal sottoscritto, per eseguire la verifica sperimentale della legge di Hooke. A questo scopo si utilizza un sostegno in metallo, una molla scelta fra le cinque (di diversa costante elastica) contenute nella scatoletta di cartone bianco, diverse masse ed un'asta graduata tenuta in piedi da un sostegno metallico. Si sospende la molla al treppiede e si verifica l'allungamento rispetto alla posizione di equilibrio, quindi si pongono in ascissa questi allungamenti e in ordinate i pesi, verificando facilmente la loro diretta proporzionalità. Semplice, no?
	Lo scatto illustra una molla a spirale, che può essere usata per dimostrare come il momento torcente sia proporzionale all'angolo di torsione, esattamente come la forza traente è proporzionale all'allungamento per la molla lineare. Questo strumento è stato utilizzato negli orologi da tasca e da polso (vedi).
	Questo altro non è che un pendolo, fabbricato sospendendo una massa ad un sostegno con un filo di lunghezza opportuna per poter eseguire la misura dell'accelerazione di gravità terrestre. Basta far compiere al pendolo dieci oscillazioni e misurarne la durata con un cronometro, ripetere la misurazione per cinque volte, eseguire una media, dividere per dieci ed infine adoperare la semplice legge del moto armonico per misurare g con un errore inferiore al 10 %. Impossibile tenere un corso liceale di meccanica senza far eseguire quest'esperienza agli allievi.
	Un'asta orizzontale, uno strumento di misura molto semplice che può essere utilizzato per misurare l'ampiezza delle oscillazioni del pendolo (le quali sono armoniche solo se l'angolo di oscillazione non supera i 10°: legge di Galilei sull'isocronismo delle piccole oscillazioni), ma anche in esperienze più complesse di ottica o di elettrologia.
	L'immagine in figura (le mani sono quelle del mio allievo Edoardo Tovaglieri) illustra il fenomeno della rottura a fatica. Un tondino di metallo è molto difficile da spezzare, ma non se lo si piega e ripiega più volte in direzioni opposte. Il metallo infatti subisce un fenomeno chiamato snervamento ed alla fine si rompe. Il fenomeno fu scoperto a metà ottocento in seguito a un grave incidente ferroviario, che era stato provocato proprio dalla rottura a fatica di un assiale che, girando, era sollecitato in continuazione a trazioni e compressioni ripetute. In figura è il refil di una biro ad essere spezzato a fatica.
	Questa fotografia ripresa dall'allieva Marta Milano mostra sulla destra un grosso disco metallico tenuto in posizione verticale, sulla cui superficie viene steso e trattenuto un foglio di carta ritagliato in forma circolare. Alle due carrucole disposte sulla periferia del disco vengono sospese delle masse, le quali equilibrano una terza massa collegata al gancio del punto di connessione tra i due fili. Per esempio, appendendo 300 g e 400 g alle due carrucole e 500 g al gancio centrale, à immediato verificare che l'angolo formato dai due cavi obliqui è retto, in base alla legge di composizione dei vettori.
	L'immagine rappresenta l'oggetto visibile sulla sinistra nella foto precedente, e cioè il cosiddetto tavolino di Varignon: un altro apparecchio per mostrare in modo semplice la composizione di forze concorrenti. Notevole in quest'esemplare è il goniometro sul piatto orizzontale, che permette una verifica quantitativa anche della somma vettoriale di forze il cui valore non viene a comporre angoli notevoli (di 30°, 45°, 60°). Accanto allo strumento si vedono anche delle masse da utilizzarsi negli esperimenti.
	La fotografia in esame illustra un altro dispositivo per visualizzare in maniera semplice ed efficace il parallelogramma delle forze. Come si vede è stato montato un telaio al quale sono appesi un ripiano verticale, sul quale è fissato un goniometro, e due carrucole che tengono sospese masse di 3 e 4 hg, mentre la massa sospesa al centro è di 5 hg. In base alle leggi del calcolo vettoriale, l'angolo che si forma è di 90°, come si verifica facilmente.
	Un'altra verifica delle leggi del calcolo vettoriale si può effettuare con la disposizione in figura, in cui le due carrucole tengono sospese due masse, entrambe di 3 hg, mentre al centro sono sospesi altri 3 hg. In questo caso le tre forze sono uguali in modulo, e quindi il parallelogramma da esse descritto è un rombo formato da due triangoli equilateri con un lato in comune. Se ne deduce che le tre forze debbono essere separate da tre angoli di 120°, come il goniometro dimostra assai facilmente.
	Questa foto mi è stata messa a disposizione dalla collega Elena Ricci, che ringrazio vivamente (questo il suo sito), e raffigura un altro modo per eseguire l'esperienza della composizione delle forze. In pratica si appende ad un perno del sostegno il dinamometro cui sono sospesi alcuni pesetti, quindi si aggancia all'estremità del dinamometro un filo che passa nella gola di una puleggia ed a cui sono sospesi altri pesetti. Mediante un goniometro si misurano gli angoli formato dalle forze peso e dalla relativa equilibrante al variare delle forze (basta aumentare o diminuire i pesetti), e verificare la legge di composizione vettoriale diventa davvero uno scherzo.
	L'immagine in esame, ripresa dai miei studenti di Seconda Liceo Classico, illustra un'esperienza semplicissima ma assai suggestiva: la verifica del parallelogramma delle forze sul piano inclinato. Un carrellino appesantito opportunamente è posto su di un piano inclinato realizzato mediante la guida metallica ed alcuni libri; il dinamometro misura la componente tangenziale della forza peso, e permette di verificare la scomposizione della forza lungo due direzioni.
	Ed ecco un altro modello di piano inclinato, che non ha bisogno di libri o simili per essere sorretto. La sua pendenza è regolabile, e grazie ad un goniometro è possibile leggere l'angolo che esso forma con l'orizzontale. In tal caso la componente della forza peso parallela al piano è dato dal peso dell'oggetto posto sul piano per il seno di questo angolo, mentre la componente perpendicolare al piano è data dal peso il coseno del suddetto angolo.
	Qui vedete il piano inclinato della foto precedente all'opera, per dimostrare la scomposizione dei vettori: esso è inclinato esattamente di 30°, su di esso si pone un carrellino con una massa di 150 g ed un pesetto da 50 g, per un totale di 200 g; ad esso si lega una fune che passa sulla carrucola, e all'altra estremità c'è una massa di 100 g, dimostrando così che la componente del peso parallela al piano inclinato è pari al prodotto del peso per il seno dell'angolo di inclinazione, dato che sen 30° = 0,5!
	Un modello dimostrativo di turbina (più sotto ne vedremo una di ben altre dimensioni) permette di verificare la scomposizione delle velocità. Infatti un getto d'acqua ad alta velocità investe le pale della turbina, che però sono inclinate di 45°; la velocità delle molecole d'acqua è allora scomposta in due componenti, una perpendicolare al getto ed una inclinata di 135° rispetto ad esso. La prima devia le molecole d'acqua, la seconda spinge le pale e mette in rotazione la turbina.
	La fotografia qui a fianco rappresenta l'esperienza che permette la verifica della legge oraria del moto armonico. In pratica si sospende una molla ad un sostegno, la si carica con una massa facendo attenzione a non snervarla, la si fa oscillare, si contano dieci oscillazioni e poi si divide il risultato per dieci, trovando il periodo del moto armonico. Note la costante elastica della molla (già misurata) e la massa sospesa, si trova facilmente un valore teorico del periodo di oscillazione, da confrontare con il valore sperimentale.
	Quello qui fotografato dalla mia allieva Sara Scampini (5 G a.s. 2011/12) nel Museo Galileo di Firenze è un telaio di legno a forma di cicloide. Lasciando cadere simultaneamente due palline lungo di esso e lungo il piano inclinato rettilineo, si osserva che la pallina lungo l'arco di cicloide anticipa nettamente quella lungo il piano inclinato. In tal modo si dimostra che il percorso congiungente due punti lungo il quale un grave scende nel tempo minore (brachistocrona) è proprio un arco di cicloide, e non un segmento o un arco di cerchio, come fu dimostrato da Jacques Bernoulli nel 1697.
	Sempre presso il Museo Galileo di Firenze è possibile ammirare questo ingegnosissimo apparecchio atto a dimostrare la legge della caduta dei gravi lungo un piano inclinato. Sopra una base esagonale in legno sono montate sei aste ricurve di ottone che formano un paraboloide, attorno al quale corre un binario a spirale. Si lascia cadere una biglia lungo il binario e, quando essa ha percorso la prima spira, viene lasciata cadere una seconda biglia; si osserva così che ogni spira viene percorsa dalle due biglie in tempi uguali, esattamente come previsto dalla legge galileiana del moto uniformemente accelerato dei gravi!
	Ed ecco un classico esempio di paradosso meccanico: su due binari di legno è appoggiata una coppia di coni dello stesso materiale, uniti lungo le loro basi. Ponendo il doppio cono sulla parte inferiore del telaio, esso inizia spontaneamente a salire verso l'alto, dando così l'impressione di contraddire la legge di Gravitazione Universale! Il paradosso però è solo apparente: dato che i binari sono divaricati, il baricentro del doppio cono non sale mentre l'oggetto sembra rotolare verso l'alto, ma scende sempre! Cliccando qui potrete vedere un breve filmato che lo mostra all'opera.
	Lo strano scatto qui a fianco mostra mia mamma, la prof.ssa Enrica Soldavini, intenta ad un'azione molto comune tra le casalinghe: sta asciugando l'insalata in giardino, dopo averla lavata e prima di portarla in tavola. Che ci crediate o no, si tratta di un'evidente applicazione del primo principio della dinamica o principio d'inerzia. Infatti, sbattendo violentemente l'insalata bagnata dentro uno strofinaccio, l'umidità, a cui lo straccio è permeabile, mantiene il proprio stato di moto rettilineo uniforme (a differenza dell'insalata, bloccata dentro lo strofinaccio) venendo spruzzata all'indietro, e così l'insalata si asciuga.
	Come afferma il secondo principio della dinamica, alla base di quasi tutti i problemi dinamici, la forza applicata ad un corpo è direttamente proporzionale all'accelerazione da esso assunta, e la costante di proporzionalità diretta è la massa. In questa figura vediamo una serie di masse, alcune anche con sostegno e gancio, per effettuare varie esperienze di dinamica.
	Il disegno in esame, nel quale è inserita anche una miniatura dell'esperienza vera e propria, si deve agli alunni Filippo Puricelli e Cecilia Spampinato (II B cl. a.s.2007/2008), ed illustra il meccanismo per la verifica sperimentale del secondo principio della dinamica. La verifica è effettuata facendo in modo che il carrellino, di massa nota, venga trascinato da una massa in caduta libera a cui è collegato tramite un filo. Misurando l'accelerazione è facile verificare la veridicità della legge fisica.
	Questo magnifico cannone è stato fotografato dall'autore di questo sito il 23/05/2013 al Museo Nazionale della Scienza e della Tecnica di Milano, nella sezione navale. Cosa ci fa qui? Quello che ci interessa ora sono le sue... ruote. Infatti, quando il cannone sparava, il rinculo lo spostava bruscamente all'indietro, e da qui la necessità delle ruote. Il rinculo è una conseguenza diretta del terzo principio della dinamica (o legge di azione e reazione).
	Quest'immagine quadripartita rappresenta una semplicissima esperienza riguardante il terzo principio della dinamica, da eseguirsi con materiale povero: uno stuzzicadenti, un cerino, carta stagnola. Si arrotolano insieme strettamente il cerino e lo stuzzicadenti, dopo aver tagliato in dimensioni adeguate la stagnola, quindi si pone lo stuzzicadenti in equilibrio sul pacchetto di cerini come mostrato in basso a destra. Avvicinando all'estremità inferiore della stagnola un cerino acceso, lo stuzzicadenti parte come... un missile, poiché la combustione del cerino in ambiente chiuso indirizza il getto di gas combusti verso il basso, e di conseguenza il tutto tende a muoversi in direzione opposta, partendo verso l'alto!
	Questa fotografia sembra stare tra le circostanti come i cavoli a merenda, invece ha un preciso significato fisico. Si vede infatti il cruscotto della mia auto che procede sotto la fitta nevicata del 26 gennaio 2006. I tergicristalli sono in funzione e la neve sembra cadere proprio perpendicolarmente al cruscotto. Vento forte e bufera di neve? No, semplicemente il moto di caduta verticale dei fiocchi di neve si compone verticalmente con il moto orizzontale dell'auto, ed il risultato è questo: la neve che sembra "venire incontro" all'auto. È lo stesso motivo per cui occorre inclinare l'ombrello in avanti quando si corre sotto la pioggia: una chiara ancorché semplice applicazione del moto relativo.
	Uno straordinario quanto datato dispositivo: un parallelogrammo articolato in grado di dimostrare le leggi della statica. Fino a che il pendolino, sospeso nel baricentro, resta all'interno della base, il parallelepipedo rimane in equilibrio, ma esce dall'equilibrio e cade non appena il pendolo esce dalla base di appoggio, come si può vedere in questo video da me realizzato. In pratica è la dimostrazione del perchè la torre di Pisa pende ma non cade!!
	Questa immagine composita mostra un divertente giochetto prestatomi dalla mia allieva Francesca Piotti (III B cl. a.s. 2008/09) che illustra il fenomeno dell'equilibrio. Questa biciclettina di metallo e questa pallina dello stesso materiale paiono del tutto diverse tra di loro, tuttavia il dispositivo è fabbricato in modo che esso possa restare perfettamente in equilibrio sul suo supporto, su una biro o su un polpastrello. Il punto di appoggio dell'oggetto sospeso coincide con il suo baricentro. Ecco in proposito un breve filmato che mostra questo perfetto equilibrio.
	Un altro curioso giocattolo, da noi acquistato negli Stati Uniti d'America, è quest'aquila dalla testa bianca (Haliaeetus leucocephalus), famosa perchè campeggia sullo stemma degli USA dal 1782. Come si può vedere, essa resta in perfetto equilibrio stabile una volta appoggiata su un piedistallo per mezzo della punta del becco. Anche in questo caso è tutta questione di baricentro: quest'ultimo si trova proprio nel becco, grazie alle ali particolarmente spesse e pesanti!
	Questa foto composita mostra altri divertenti esempi di giocattoli il cui funzionamento si basa sull'equilibrio dei corpi: sia la libellula in basso a sinistra che i cavallini in alto a sinistra che l'omino a destra si reggono in equilibrio grazie alla lunga coda che, negli ultimi due casi, è appesantita in modo da spostare il baricentro verso il basso. Queste curiose applicazioni della Statica sono state realizzate da studenti del mio Liceo!
	Questo divertente giocattolo mostra un esempio di pupazzo che oscilla e resta in piedi in qualunque modo lo si sposti dalla posizione di equilibrio (ricorda il celebre "Ercolino sempre in piedi", regalato negli anni settanta con i punti dei formaggini Galbani). Ciò può avvenire grazie alla forma arrotondata della sua base e alla distribuzione del suo peso, il quale fa sì che il baricentro si trovi molto in basso (in effetti, il clown è ripieno di sabbia). Quando il pupazzo viene inclinato, anche di un angolo notevole, il suo peso agisce da forza di richiamo verso la posizione verticale.
	L'immagine raffigura il classico strumento da laboratorio utilizzato per determinare la posizione del baricentro di un corpo, per esempio una lamina metallica a forma di cerchio o di triangolo. Dato che la verticale passa sempre per il baricentro, basta sospendere la lamina in posizioni differenti e tracciare la verticale, segnata da un filo a piombo. Tutte le verticali tracciate passano per il baricentro, che dunque è estremamente facile da individuare.
	Questo treppiede ci permette di introdurre una delle proprietà fondamentali della statica dei corpi: l'isostaticità. Un corpo si dice isostatico quando possiede un numero di vincoli pari ai suoi gradi di libertà. Ad esempio, una porta libera di girare sui cardini non lo è, perchè ha tre gradi di libertà ma solo due vincoli, e può ruotare intorno ai cardini. L'oggetto posto su questo treppiede ha anch'esso tre gradi di libertà, ma altrettanti vincoli, rappresentati dagli appoggi sul terreno: infatti il treppiede non si rovescia. Un tavolino a quattro gambe, invece, ha tre gradi di libertà e quattro vincoli, e quindi si dice iperstatico. Tutto questo è alla base della moderna Scienza delle Costruzioni.
	L'equilibrio dei corpi ci trasporta immediatamente nell'ambito della statica, capitolo fondamentale della Scienza delle Costruzioni. Nell'immagine a fianco vediamo un esempio di capriata, un tipo di copertura delle costruzioni che ha avuto molta fortuna nel passato, specie se decorata con intagli o decorazioni geometriche. È un elemento fondamentale della scienza delle costruzioni, perché assicura la ripartizione sui suoi punti d'appoggio dei pesi della copertura (e dell'eventuale neve sopra di essa)
	La capriata venne usata in epoca paleocristiana come copertura per le prime basiliche cristiane, perché ha il vantaggio di annullare le spinte orizzontali grazie alla sua struttura intelaiata, ed il fatto di non generare spinte laterali permetteva di avere mura lisce, senza bisogno di contrafforti, adatte per essere affrescate con temi sacri. Poco in uso durante il Rinascimento, la capriata ha conosciuto una seconda giovinezza nell'età moderna grazie agli edifici in ferro e in ghisa costruiti per scopi industriali. A fianco si vede un modellino di tempio con copertura a capriata realizzato dagli studenti del mio Liceo.
	Ed ecco una seconda fondamentale struttura architettonica: l'arco. In essa i materiali da costruzione (blocchi di pietra, mattoni, ecc.) sono disposti l'uno sull'altro in modo da scaricare lateralmente il peso della muratura sovrastante, riducendo lo sforzo di flessione dei materiali. Quello in figura è un arco a sesto acuto o ogivale, da me fotografato (come la capriata soprastante) nel santuario di S.Maria a Brunello (VA) con il permesso del rettore, il mio amico don Gianni Pianaro, che ringrazio.
	Nella Biblioteca del mio Liceo la gentile bibliotecaria, prof. Rosita Rioda, mi ha concesso il permesso di fotografare questo fantastico modellino di una tomba etrusca a cupola rinvenuta a Casale Marittimo (provincia di Pisa), realizzato dagli studenti nelle ore di Arte. Si vede il principio costruttivo della cupola, che poi è lo stesso dell'arco appena visto: incastrare i massi l'uno nell'altro in modo da scaricare tutto il peso sul perimetro laterale. Per rinforzare il tutto qui c'è un pilastro centrale.
	Una cupola assai più grande e più perfezionata è quella di Santa Maria del Fiore a Firenze, che qui vediamo in un altro modellino esposto nella Biblioteca del mio Liceo, e dovuta all'abilità degli studenti Elena Borgo e Jacopo Orsini (IV B a.s. 2005/2006) . Il duomo fu iniziato nel 1296 dal grande architetto Arnolfo di Cambio, e completato nel 1434 da Filippo Brunelleschi (1377-1446) con la monumentale cupola, conclusa però solo nel 1461. La lanterna dista 107 m dal suolo, e il duomo è la seconda chiesa del mondo per grandezza dopo San Pietro a Roma. L'immensa cupola ha pianta ottagonale, è a sesto acuto e scarica ingegnosamente tutto l'enorme peso sui contrafforti laterali.
	Quella che qui vedete illustrata è una guida metallica usata per vari esperimenti sulla caduta dei gravi, analoghi a quelli condotti da Galileo Galilei. Le due aste graduate alle estremità della guida servono per misurare le rispettive altezze rispetto al piano del bancone, e quindi il dislivello coperto dalla pallina scivolando lungo la guida. Le due masse da 5 Kg ciascuna poste sui treppiedi servono ad impedire che il peso della guida li faccia ribaltare; la scanalatura della guida poi rendono poi minimo l'attrito. Questa guida può servire ad esempio per dimostrare, nell'ambito degli errori sperimentali (a causa dell'ineliminabile attrito), il...
	...il principio di conservazione dell'energia. In pratica si fa rotolare una sferetta d'acciaio lungo la guida (sulla destra di questa foto) e poi la si fa ricadere, con una traiettoria parabolica, sopra un foglio di carta carbone capovolto, in modo che lasci una traccia ben visibile sul bancone o sul pavimento (maggiore è il dislivello, maggiore sarà la precisione). Nota l'altezza della traiettoria parabolica e la gittata (rilevabile grazie alla suddetta traccia), si ricava la velocità della pallina al momento in cui lascia la guida, e quindi la sua energia cinetica; risulta immediato risalire così alla costanza dell'energia meccanica totale. Se gli studenti osservano una differenza di energia tra l'inizio e la fine, è immediato imputarla all'attrito.
	Una facilissima esperienza eseguita dai miei alunni di Seconda Liceo Classico: ponendo il blocco sulla guida di legno, esso non scivola anche inclinando la guida a causa della presenza dell'attrito statico; il blocco comincia a scivolare solo quando si raggiunge una certa pendenza. È disponibile anche un filmato digitale di quest'esperienza.
	Come è possibile determinare il coefficiente di attrito statico del legno su legno? Misurando la cosiddetta "forza di primo distacco", cioè la minima forza necessaria a muovere il blocco di legno. Per questo basta tirare il blocco con un dinamometro; la forza da esso segnata quando inizia il moto è la forza di primo distacco, cioè la forza d'attrito. Dividendo tale forza per il peso del blocco si ottiene agevolmente il coefficiente di attrito statico.
	Questa foto mostra l'apparato sperimentale per misurare il coefficiente di attrito radente tra un blocco di legno ed una guida dello stesso materiale. Il blocco è messo in moto da un peso in caduta libera, legato ad esso per mezzo di un filo di nylon; dato che la guida di legno non ha i rebbi per incastrarvi una carrucola, essa è stata sovrapposta ad una guida in metallo. La velocità del blocco è misurata mediante un marcatempo elettromagnetico (vedi sopra) e, con facili considerazioni energetiche, è possibile ricavare il coefficiente di attrito legno-legno.
	Come mostra quest'altra fotografia, con il suddetto apparato sperimentale, oltre al coefficiente di attrito legno-legno è possibile calcolare quello legno-panno e quello legno-plexiglas, essendo due facce del blocco ricoperte di questi materiali. Si noti che due facce del blocco, una più larga ed una più stretta, sono di legno senza ricoperture per verificare che il coefficiente d'attrito è indipendente dall'ampiezza delle superfici a contatto.
	L'attrito volvente è circa cento volte più piccolo di quello radente. Mentre quest'ultimo è una conseguenza del reciproco strisciamento di due corpi solidi, quello volvente è dovuto al rotolamento dell'uno sull'altro. È così piccolo perchè anche la superficie di contatto tra i due solidi è piccolissima! Tuttavia è da notare che civiltà avanzatissime come quella Maya sono riuscite a mettere a punto calendari precisissimi e ad edificare imponenti costruzioni senza mai far uso della ruota!
	Questa pinza viene utilizzata in meccanica, termodinamica e chimica per trattenere componenti di apparati sperimentali o per sospendere provette sopra i Bunsen. Perchè si trova in questa posizione dell'Armadio Virtuale? Perchè essa trattiene gli oggetti mediante una vite senza fine o vite di Archimede. La vite funziona mediante il principio dell'attrito; non si svita da sola, cioè, a causa del forte attrito prodotto contro il bullone dal filetto, una sorta di piano inclinato avvolto attorno alla vite.
	Sulla sinistra, ecco un modello di pendolo di Foucault, con il quale il fisico francese Jean Bernard Leon Foucault (1819 – 1868) dimostrò il moto di rotazione della Terra dal . Posto il pendolo in oscillazione in un piano verticale, ma libero di ruotare, a causa del moto di rotazione della Terra il piano di oscillazione ruota leggermente rispetto al terreno sottostante, perchè il pendolo tende a conservare immutato il piano di oscillazione rispetto ad un sistema di riferimento assoluto. Il tutto è montato su di una macchina di rotazione a mano.
	Questa foto differisce dalle altre della galleria, pur rappresentando una versione in scala maggiore del pendolo di Foucault di cui si è detto sopra, perchè è stata scattata nel padiglione astronomico del Museo Nazionale della Scienza e della Tecnica di Milano, visitabile online al sito www.museoscienza.org: ci sono stato con la III A e la III B cl. a.s. 2004/05 il 26/02/2005. Cliccando qui invece potreste scaricare un breve filmato che mostra il pendolo di Foucault del Museo delle Scienze Principe Felipe di Valencia, ripreso il 27/08/2023 dalla mia studentessa Valentina Chimento (3 C a.s. 2022/23)
	La fotografia illustra un oggetto davvero raro da trovare in un laboratorio liceale: un modellino di bilancia di torsione o bilancia di Cavendish. Si tratta del dispositivo ideato da Henry Cavendish (1731-1810), lo scopritore delll'idrogeno, per misurare la costante di gravitazione universale. Le due sfere massicce vengono avvicinate alle sfere più piccole, poste alle estremità di una bacchetta (equipaggio) sospesa ad un filo e chiusa dentro una scatola di plexiglas per ripararla dalle correnti d'aria; misurando la lievissima torsione della bilancia mediante lo specchietto solidale al filo, su cui si fa incidere un raggio di luce, è possibile misurare l'attrazione gravitazionale tra le due sfere, e quindi la costante G.
	La ricostruzione pittorica qui a fianco è dovuta al mio studente Tommaso Alfonsi (4 G a.s. 2010/11), che per realizzarla si è servito del programma Google SketchUp. In essa è rappresentato il campo gravitazionale terrestre: una massa "deforma" lo spazio circostante esattamente come una palla da bowling posta su un letto ne deforma la superficie. Il percorso più breve tra due punti in questo spazio "deformato" non è più rettilineo, ma un arco di curva. Questo spiega perchè la Luna si muove di moto curvilineo attorno alla Terra, essendo costretta a spostarsi nel "pozzo gravitazionale" da essa formato!
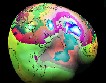
	Il satellite GRACE (Gravity Recorder and Climate) ha ripreso quest'insolita immagine della Terra rilevando le differenze nell'attrazione gravitazionale da un punto all'altro della sua superficie. Ne consegue che la Terra è tutto, fuorché un pianeta omogeneo al suo interno... Per maggiori informazioni sulla meccanica celeste visitate l'Armadio di Geografia Astronomica.
	Vi mostro un'esperienza incredibilmente semplice per misurare l'accelerazione centripeta, nella fattispecie del piatto di un giradischi (da qui potete scaricare la scheda di laboratorio). Non tutti lo sanno, ma ogni smartphone contiene un accelerometro. Io ho scaricato l'app Pysics Toolbox Sensor Suite, ne ho attivato l'accelerometro, l'ho posto sul piatto del giradischi del mio Hi-fi, l'ho fatto girare a 45 giri al minuto, quindi l'ho fermato, ho letto l'accelerazione misurata dal sensore (cliccate qui per vedere la mia lettura) e la ho confrontata con quella calcolata per via teorica. La somiglianza tra i due valori è stata confortante, e quindi la mia esperienza è riuscita! Wow!
	Questa foto di una giostra scattata in un parco divertimenti da Lorenzo Mainini spiega perfettamente il concetto di forza centrifuga, cioè quella forza apparente avvertita dai sistemi non inerziali in moto rotatorio. Un osservatore esterno, in questo caso il fotografo, vede che il trenino ruota di moto circolare uniforme, e perciò su di esso agisce una forza che lo costringe a ruotare, detta forza centripeta perché diretta verso il centro. Invece il bambino sulla giostra vede il trenino in quiete rispetto a se stesso, ma avverte una forza centripeta . Essendo il corpo in quiete, per l'osservatore sulla giostra deve esistere una forza che la controbilanci, e la chiamerà forza centrifuga, perché diretta verso l'esterno.
	Ed ecco a voi una semplicissima esperienza, da eseguirsi nel laboratorio della scuola, la quale fa uso di una macchina di rotazione a motore, cioè di un dispositivo in grado di mettere in rapida rotazione qualunque sistema meccanico, onde verificare gli effetti della forza centrifuga, che sembra far allontanare gli oggetti dall'asse di rotazione, se guardati dal punto di vista di un osservatore non inerziale. A che serve lo strano dispositivo montato su tale asse nella figura in questione?
	Ecco la risposta: come illustra la foto, serve per dimostrare lo schiacciamento polare terrestre dovuto al suo moto di rotazione. Gli anelli di metallo sostenuti dall'asse in rotazione sono flessibili e, quando la macchina entra in rapida rotazione, appaiono visibilmente schiacciati in direzione verticale a causa della forza centrifuga che spinge verso l'esterno la zona equatoriale. Un esperimento di sicuro successo, che spiega come mai più un corpo è rapido a ruotare su se stesso, più appare schiacciato ai poli, come accade ai pianeti Giove e Saturno (vedi l'Armadio Virtuale di Astronomia). Di quest'esperienza è disponibile anche un breve filmato digitale.
	La forza centrifuga può essere verificata anche con questi accessori detti anelli centrifughi: montandoli sulla macchina di rotazione, essi risultano schiacciati perchè le estremità sono soggette per l'appunto a spinta centrifuga!
	Il sottoscritto ha fotografato anche questo dispositivo per la verifica della forza centrifuga: ponendolo sulla macchina di rotazione e facendola girare, si osserva come le palline sono spinte all'estremità proprio dall'esistenza della forza apparente nota come forza centrifuga, che è anche alla base per esempio delle normali lavatrici.
	Sempre la forza centrifuga è alla base dell'ingegnoso regolatore di Watt qui ritratto, che James Watt (1736-1819) ideò per regolare l'afflusso di vapore nel motore da lui inventato, perfezionando la macchina a vapore di Newcomen. Se il vapore è in eccesso, la macchina gira troppo velocemente e rischia di esplodere, ma la forza centrifuga porta all'apertura dei due bracci, la quale agisce su una valvola che limita l'erogazione del vapore; se il vapore diminuisce troppo, i bracci si abbassano a causa della diminuzione della velocità, e la valvola si riapre. Geniale, no? Per vedere il regolatore in azione sotto l'effetto della forza centrifuga, scaricate questo breve filmato.
	Anche questa fotografia composita sembra non avere alcuna relazione con le precedenti, ma non è così. Si vede infatti mia madre che prepara un piatto di carote crude finemente tagliuzzate usando un comune robot da cucina. Come si può vedere, esso sfrutta una lama circolare (in alto a sinistra) contro la quale vengono poste (in alto a destra) e poi premute (in basso a sinistra) le carote; una volta tolta la lama, si può vedere come le carote sono state lanciate contro le pareti del robot, sempre per effetto dell'immancabile forza centrifuga. Per la serie: la Fisica in Cucina!!
	Qui vediamo illustrata un'altra forza apparente, stavolta la forza di Coriolis. Descritta per la prima volta nel 1835 dal fisico francese Gaspard Gustave de Coriolis (1792-1853), essa agisce in un sistema di riferimento in moto circolare rispetto a un sistema di riferimento inerziale. Essa dipende dalla velocità del corpo rispetto al sistema di riferimento rotante e dalla velocità angolare del sistema di riferimento rotante rispetto a quello inerziale. Il fatto che la si osservi sulla terra è una dimostrazione del fatto che il nostro pianeta ruota rispetto al sistema di riferimento delle stelle fisse. Qui la vediamo all'opera nel generare un vortice quando l'acqua scende da una bottiglia ad un'altra! Lo potete vedere anche in questo breve filmato digitale.
	Ed ecco un bellissimo esemplare di giroscopio. Si avvolge uno spago intorno all'asse di rotazione e poi lo si tira, in modo da farlo girare a grande velocità. Il giroscopio comincia a vorticare su se stesso con l'asse in posizione verticale, poi quest'ultimo comincia a ruotare descrivendo un doppio cono; tale moto è chiamato di precessione, ed è dovuto al momento della forza peso applicata nel suo baricentro. Si tratta dello stesso fenomeno che produce la precessione degli equinozi del pianeta Terra; in tal caso la precessione è dovuta all'attrazione solare.
	Questo dispositivo sperimentale è stato realizzato dal sottoscritto con alcuni pezzi del meccano con cui giocavo da bambino (mai buttare niente!!), ed illustra facilmente la trasmissione della quantità di moto durante gli urti centrali. Se sollevo il primo pendolo e lo lascio cadere sul secondo, solo l'ultimo si solleverà, perchè la quantità di moto del primo si trasmette da un pendolo all'altro. Il fenomeno non ha luogo se fra due palline viene interposto un dischetto di materiale deformabile.
	Questa è una versione più "tecnologica" dell'apparecchio sopra rappresentato. Cliccando qui potete scaricare un piccolo filmato digitale che ne illustra il funzionamento: se si solleva una pallina a sinistra, vedremo sollevarsi una pallina anche a destra; se solleviamo due palline a sinistra, se ne solleveranno due anche a destra; sollevando tre palline a sinistra, ne vediamo muoversi tre anche a destra, e così via. La quantità di moto infatti si conserva, e dunque a destra si sollevano esattamente tante palline quante ne alziamo dalla parte opposta! Una verifica davvero convincente di questo principio di conservazione.
	Questa specie di bilancia può venire utilizzata per studiare i tre stati di equilibrio, ed in particolare l'equilibrio instabile. Infatti lo stelo è diviso in due parti, e la parte superiore ha un'estremità convessa che alloggia dentro quella concava della parte inferiore. L'equilibrio appare dunque instabile come quello di una matita tenuta in bilico sulla punta, ma la presenza dei due contrappesi laterali permette ai bracci della bilancia di restare in equilibrio, spostando il baricentro dell'oggetto. Un esperimento intuitivo ma molto significativo persino per i bambini.
	In una sala del Museo Galileo di Firenze è possibile vedere questa bilancia pesapersone a bracci disuguali. All'estremità del braccio sinistro c'è una gabbia in legno nella quale veniva fatta sedere la persona da pesare, mentre all'altra estremità vi è un piatto in rame porta pesi. L'oggetto proviene dalle collezioni granducali, e la foto è stata scattata dalla mia allieva Sara Scampini (5 G a.s. 2011/12). Ma chi lo ha detto che la gente bada alla propria linea soltanto da quando è iniziata l'era del benessere con il boom economico?
	Ed ora, alcune interessanti esperienze sulle macchine semplici dette leve. In particolare, quella in figura è una leva di primo genere perchè ha il fulcro tra la resistenza e la potenza: è il principio della comune bilancia a bracci uguali. Noi sappiamo che l'equilibrio rotazionale è assicurato se la somma vettoriale dei momenti è pari a zero. Questo significa che, se appendo masse uguali ai due bracci della bilancia, devo appenderle ad ugual distanza dal fulcro. Semplice, no?
	Se invece poniamo sui bracci della bilancia masse diverse, sicuramente dobbiamo porle a diversa distanza dal centro , come illustra assai bene questa fotografia. Come si vede, sul braccio destro la massa è tre volte più grande che sul sinistro; questo implica che il braccio di sinistra deve essere tre volte più lungo di quello destro, a causa della inversa proporzionalità tra lunghezza dei bracci e forze applicate, che consegue dalla condizione di equilibrio rotazionale!
	Ed ecco un esempio più complesso. Il sistema a sinistra è in equilibrio rotazionale. Considerando infatti positivi i momenti che ruotano in senso antiorario e negativi quelli in senso orario, a sinistra ho un momento m x 6b + 2m x 3b = 12 m b, dove m è ciascuna delle masse appese e b la distanza tra due ganci sui bracci della leva. A destra invece ho - 2m x 6b = - 12 m b. Come si vede i due momenti sono uguali ed opposti, e quindi il sistema resta in equilibrio!
	Nella foto accanto si vede come è possibile realizzare in laboratorio un modello di leva di secondo genere facendo ricorso alla stessa strumentazione delle esperienze precedenti. In questo caso è necessario utilizzare un telaio con carrucole: il filo che passa su di esso è agganciato all'estremità del braccio della leva di primo genere, e rappresenta la potenza, mentre la resistenza è agganciata a metà dello stesso braccio. Come si vede, una sola massa è in grado di tenere in equilibrio due ad essa uguali, dimostrando in modo incontrovertibile che la leva di secondo genere è sempre vantaggiosa.
	Analogamente è facile realizzare anche un modello di leva di terzo genere: il filo che si avvolge sulle carrucole è ora agganciato alla metà del braccio. Come si vede chiaramente, per tenere in equilibrio una sola massa agganciata all'estremità del braccio ne sono necessarie due appese all'altro capo del filo, dimostrando che la leva di terzo genere è sempre svantaggiosa. Naturalmente se la potenza (il filo) fosse stata agganciata non a metà ma ad un terzo della lunghezza del braccio, sarebbe sta necessaria una potenza pari a tre masse per tenerne in equilibrio una sola. Il concetto vi è chiaro?
	Un semplicissimo esempio di leva di primo genere è fornito dalle forbici, così come dalle tenaglie, dal tronchesino usato per il filo spinato, dalle grandi forbici per potare i rami degli alberi, ecc. Infatti in tutti questi strumenti il fulcro è compreso tra l'oggetto da tagliare (resistenza) e le nostre dita (potenza). Più i manici sono lunghi, maggiore è la potenza con cui l'oggetto viene reciso: ecco perchè i tronchesini hanno dei manici così grossi!
	Altro esempio di leva di primo genere è rappresentato dalla stadera, un particolare tipo di bilancia, le cui origini affondano in epoca romana e forse sannita. Mentre una comune bilancia ha i bracci di lunghezza fissa (di solito uguali tra loro), in questo caso è fisso solo il braccio della resistenza; quest'ultima è rappresentata dal piatto sostenuto da catene, su cui si pone l'oggetto da massare. Ad essere fissa è invece la potenza, rappresentata da un peso chiamato Romano, avendo un tempo la forma di una testa di romano. Per ottenere l'equilibrio si fa scorrere il Romano sul braccio della potenza, che è stato già tarato in unità di massa. Posso pubblicare questa foto grazie alla cortesia dell'allievo Gabriele Bof (1 G a.s. 2011/12) che l'ha scattata.
	Anche la carrucola semplice (eccone due modelli datati) è una leva di primo genere: infatti il fulcro sta in mezzo, dove la carrucola è incernierata nel perno; la resistenza è la forza peso della massa da sollevare; la potenza è la forza di chi solleva; ed il fulcro sta evidentemente in mezzo tra resistenza e potenza. Si tratta in particolare di macchine né vantaggiose né svantaggiose, poiché per equilibrare una certa massa ne occorre una uguale. Vi è una leva di primo genere anche nel corpo umano: il cranio è sorretto dalla vertebra atlante, la resistenza (peso del cranio) tenderebbe a far inclinare la testa in avanti, la potenza è offerta dai muscoli del collo!
	Ed ecco invece un esempio rudimentale di carrucola composta, in cui la resistenza è agganciata ad una seconda carrucola (qui direttamente al filo) che a sua volta è sostenuta da una carrucola semplice. La carrucola composta rappresenta una leva di secondo genere, poiché quello che nel caso precedente era il fulcro, ora diventa la resistenza da sollevare, e si trova tra il fulcro e la potenza; inoltre il braccio della potenza è doppio di quello della resistenza (l'uno è il diametro e l'altro il raggio della carrucola sospesa), per cui con una certa massa posso equilibrarne una doppia.
	Se vogliamo un esempio di leva di secondo genere di uso comune, basterà prendere in considerazione questo modello un po' retrò di schiacciapatate, abilmente utilizzato dalle mani di mia mamma per realizzare degli gnocchi di patate. Come si vede, anche in esso la resistenza (le patate lessate da schiacciare e ridurre in pasta) è compresa fra il fulcro (la vite a destra) e la potenza (le mani della cuoca): schiacciare i tuberi con le mani richiederebbe molta fatica, invece "allungando" il braccio della potenza a parità di braccio della resistenza è possibile ridurre a piacimento la fatica in cucina!
	Questa fotografia del vecchio arcolaio di mia trisnonna (tuttora funzionante) non è fuori posto in questa rassegna, poiché esso rappresenta un ottimo modello di leva di terzo genere, in cui cioè la potenza (il piede) si trova tra la resistenza (la biella che mette in moto l'arcolaio) e il fulcro (il punto dove il pedale è incernierato). Il braccio della resistenza è maggiore di quello della potenza, quindi la leva risulta svantaggiosa; ma il suo scopo non è quello di sviluppare lavoro bensì di mettere semplicemente in rotazione l'arcolaio, per cui la soluzione costruttiva si rivela vantaggiosa.
	Un altro splendido esempio di sistema biella-manovella è quello che aziona la macchina da cucire d'epoca ritratta in questa fotografia. Come nel caso dell'arcolaio precedente, il moto alternativo del piede sul pedale viene trasformato in un moto circolare continuo dall'ingegnoso meccanismo, che viene utilizzato anche nelle locomotive per trasformare il moto alternato del pistone spinto dal vapore nel moto circolare continuo delle ruote del treno.
	Al Museo Nazionale della Scienza e della Tecnica di Milano il 23/05/2013 l'autore di questo sito ha fotografato il complesso sistema biella-manovella di questa locomotiva a vapore del Padiglione Ferroviario. In essa il vapore acque spinge alternativamente a destra e a sinistra uno stantuffo, e questo rende necessario un sistema di leve per trasformare il movimento alternato in un moto circolare uniforme, per far avanzare il convoglio.
	Un altro straordinario gioco di leve fa funzionare questo elevatore ad altezza regolabile. La manopola a sinistra comanda una vite senza fine che avvicina due bracci metallici del sistema di leve, ed allora il ripiano si abbassa; oppure le fa allontanare, ed allora si solleva. Indispensabile per eseguire molte esperienze non solo di meccanica (per es. l'esperienza di Ö ersted), ma anche utile per capire come le leve possono essere applicate alla tecnologia.
	Un ingegnoso sistema di leve era anche alla base del funzionamento di questa Lettera 42 (evoluzione della mitica Lettera 22 di Indro Montanelli), una macchina da scrivere che non necessitava di alimentazione elettrica. Premendo i tasti si mettevano in moto i battenti, che premevano con forza sul nastro (visibile al centro del piano superiore della macchina), imprimendo i caratteri sul foglio. Per imprimere le maiuscole bastava premere un tasto ed abbassare l'intero sistema di leve!
	Gli ingranaggi qui illustrati furono ideati nell'antichità e studiati con impegno e passione da Leonardo da Vinci, ma solo all'inizio dell'era industriale ci si accorse che i loro denti, per ingranare perfettamente l'uno nell'altro, dovevano avere la forma di un evolvente di cerchio. Ricordiamo che si chiama evolvente la linea tracciata dall'estremità di una corda avvolta su di una circonferenza che si srotola senza strisciare.
	Gli ingranaggi possono essere utilizzati facilmente per trasmettere il moto rotatorio a 90°; basta dare loro una forma conica. Questo è il caso dell'antico trapano a mano qui fotografato, in cui il movimento è trasmesso alla punta dalla manovella a mano grazie a due semplici ingranaggi, visibili nel particolare ingrandito. Il trapano apparteneva a mio nonno, Natale Soldavini, e per forare le assi di legno sfrutta un altro principio nella punta, quello della vite senza fine.
	Grazie ad un sistema di ingranaggi più complesso, è stato possibile realizzare questo magnifico modellino di elicottero, le cui pale ruotano agendo sulla manovella laterale; da notare che la stessa manovella comanda anche l'elica posteriore! Il modellino è stato costruito usando una scatola di costruzioni della Lego ®, che mi è stata regalata negli anni settanta!
	Questo ingrandimento della foto precedente mostra chiaramente il complesso gioco di ingranaggi che sono stati necessari per realizzare il modellino. Gli ingranaggi sono di tre tipi diversi: due hanno i denti ad evolvente di cerchio, uno di diametro grande ed uno di diametro molto più piccolo, mentre il terzo ha denti piegati a quarto di cerchio, che servono per ingranare con i precedenti a 90°. Si noti che il modello di elicottero ideato dalla Lego ® è così preciso, da avere persino la possibilità di mutare l'inclinazione delle pale (come fa un elicottero vero per cambiare direzione, per mezzo di un gioco di leve che vengono comandate dalla postazione davanti alle poltroncine nere. Ingegnoso, vero?
	Questo, fotografato in una Scuola Guida, è un suggestivo modellino di automobile (per la precisione, di un'antica Fiat 500), che mostra in bella vista il motore (a sinistra) e i meccanismi di trasmissione del moto alle ruote, ovviamente sempre attraverso alberi ed opportuni ingranaggi. Al centro si vede la scatola del cambio, a destra lil differenziale che attribuisce il moto alle ruote posteriori. Un vero pezzo vintage, se confrontato con la complessa meccanica delle automobili odierne!
	Ed ecco, ingrandito, il differenziale del modellino soprastante, organo meccanico che distribuisce la coppia motrice tra le due ruote motrici posteriori. Esso consiste essenzialmente in una coppia conica, due ingranaggi conici che possono essere affiancati con un certo angolo tra gli assi. Se l'inclinazione dei denti di ciascuna ruota è di 45°, come in questo caso, l'angolo tra gli assi è di 90°.
	Ed ecco, sempre dello stesso modellino a grandezza naturale, la scatola del cambio, che ha la funzione di modificare la caratteristica della coppia (e non della potenza) in uscita dal motore. Esso permette di selezionare di volta in volta un rapporto di trasmissione differente, a seconda della gamma di cui il cambio è dotato. Grazie a questa scatola di ingranaggi è possibile cambiare la marcia, e quindi la velocità, alla quale il veicolo procede.
	Mediante un sistema ancor più complicato di leve ed ingranaggi è possibile mettere assieme praticamente ogni macchina utilizzata dalla moderna tecnologia industriale. L'esempio più semplice è dato da questo splendido esemplare di macchina da cucire manuale, risalente agli anni '30 del secolo scorso: il sistema biella-manovella del pedale è sufficiente per mettere in moto l'ago e permettere ogni tipo di cucitura!
	A proposito di ingegnose combinazioni di ingranaggi in purissimo stile Steampunk, ecco il telaio meccanico esposto all'ingresso della città di Busto Arsizio (VA), città famosa giustappunto per le sue tessiture. Questo tipo di tecnologia meccanizzò l'arte del tessere, prima esclusivamente manuale, ed avviò la Rivoluzione Industriale, nel '700 in Inghilterra e nell'800 nell'Italia del nord.
	Ovviamente gli ingranaggi sono i componenti principali degli orologi meccanici; qui vedete uno splendido esemplare di Gallet, marca di Ginevra che produce orologi addirittura dal 1466, di proprietà del mio amico Sergio German Stinco. I primi orologi meccanici comparvero sui campanili nel Medioevo; nel 1735 l'inglese John Harrison (1693-1776) costruì il primo cronometro che permise di calcolare la longitudine, rivoluzionando la navigazione della flotta britannica.
	Grazie alla collaborazione dell'ingegner Giuseppe Biundo posso pubblicare quest'altra applicazione delle ruote dentate: nella foto composita si vede l'apparato molitorio di un vecchio mulino. Si nota l'asse di trasmissione tramite puleggia che riceveva il moto, attraverso una cinghia, da un motore elettrico da 18,5 kW di potenza visibile in basso a destra. Colpisce la particolarità dei denti delle ruote degli ingranaggi: alcuni sono in ghisa mentre altri sono di legno, dato che in questa maniera si abbassava l'attrito per via dell'incontro tra due sostanze diverse. Si notano anch e i sistemi per inserire e disinserire la rotazione della macina. Il pezzo in questione è stato prodotto dalla ditta F.lli Pagnoni di Monza.
	Un semplicissimo esperimento che però ha un enorme impatto didattico: la conservazione della quantità di moto (o "momento lineare") può essere spiegata facendo realizzare dei semplici urti anelastici fra carrellini, che restano uniti dopo lo scontro grazie alla presenza di un frammento di plastilina nella zona dello scontro. I due carrellini hanno la stessa massa e quindi, se spediti l'uno contro l'altro con la stessa velocità, si uniscono e si fermano (vedi filmato).
	Se invece uno dei carrellini ha massa doppia dell'altro, dopo l'urto si muovono insieme con velocità pari a un terzo di quella iniziale (vedi filmato). Purtroppo la verifica può essere eseguita quantitativamente solo con un sensore di velocità ad infrarossi, ed anche in questo caso l'attrito inficia irrimediabilmente l'esperienza. Tutti gli studenti però possono facilmente toccare con mano la verità di quest'affermazione in modo qualitativo, come mostra il filmato.
	Usando dei respingenti metallici che riducono notevolmente l'attrito, è facile realizzare degli urti elastici. Come si vede nel breve filmato digitale di quest'esperienza, due carrellini di massa uguale che urtano elasticamente ritornano indietro con la stessa velocità. In tal modo è facile far ricavare ai ragazzi che stavolta si conservano sia l'energia cinetica che la quantità di moto.
	È poi possibile far eseguire agli studenti molti altri esperimenti qualitativi sugli urti, facendo variare le masse dei due carrellini. Particolarmente interessante il caso in cui un carrellino venga spinto contro un altro fermo e di massa uguale: come mostra il filmato, il primo si ferma ed il secondo acquista la sua stessa velocità!
	La foto rappresenta un'esperienza che fa davvero colpo su tutti gli studenti: l'urto senza contatto. Stavolta i carrellini non hanno né plastilina né respingenti, ma due magneti orientati in modo da respingersi. L'urto avviene senza che i due carrellini si tocchino, come si può vedere nel filmato digitale corrispondente.
	Mi sembrava giusto dedicare una fotografia ai protagonisti di queste semplici esperienze sugli urti: i respingenti metallici (a sinistra) per gli urti elastici e i respingenti metallici (a destra) per quelli anelastici.
	Nel Museo Galileo di Firenze, dove è stato fotografato dalla mia allieva Sara Scampini (5 G a.s. 2011/12), si può ammirare questo apparecchio per lo studio degli urti. Al telaio sono appese delle palle di legno allineate, alcune delle quali danno vita ad urti elastici, essendo di avorio, altre ad urti anelastici, essendo di argilla. Quando la fila di sfere viene urtata da quella che si trova ad una sua estremità, la serie delle palle resta immobile e la quantità di moto viene interamente trasmessa alla palla che si trova all'estremità opposta, la quale rimbalza. Un'esperienza veramente suggestiva!
	Questi dischi e cilindri servono per esperimenti volti a misurare il momento d'inerzia di diversi corpi. I dischi e i cilindri hanno tutti un peso pressoché identico, ma una diversa distribuzione dello stesso. Possono essere utilizzati anche per esaminare le oscillazioni torsionali.
	Quello che qui vedete raffigurato è un apparecchio di rotazione ideato per verificare le leggi della dinamica rotatoria, e in particolare quella secondo cui il momento delle forze applicate ad un corpo è pari al suo momento d'inerzia per la sua accelerazione angolare. Il momento d'inerzia è quello dell'asta e delle masse ad essa fissate, mentre la forza che le mette in rotazione è quella del peso che cade, e l'accelerazione angolare media è dedotta con una semplice misurazione.
	Questo curioso soprammobile, commercializzato per decorare in modo creativo le scrivanie degli uffici, è composto da centinaia di chiodini, che permettono di modellare la forma di qualsiasi oggetto sia infilato sotto di essi: basta mettere le mani o qualsiasi oggetto sotto i chiodi, per ottenere incredibili sculture tridimensionali, come si vede usando la mia mano destra ed un modellino di Mohai dell'Isola di Pasqua ottenuto con una stampante 3D. Ma... se i chiodi pungono, perchè si può mettere tranquillamente una mano sotto di essi? Perchè la pressione della mano, distribuita su tantissimi chiodini, risulta minore, e non fa male! Ecco spiegato il segreto di tanti presunti fachiri!
	L'esistenza della pressione atmosferica può essere provata con questo semplicissimo esperimento, realizzabile in ambiente domestico utilizzando un bicchiere ed un foglio di carta (io l'ho realizzato nella lavanderia di casa mia il 6/1/2006). Basta riempire il bicchiere d'acqua per metà, chiuderlo con il foglio di carta e poi capovolgerlo (ovviamente mantenendosi per sicurezza sopra ad un lavandino). Con sorpresa si noterà che l'acqua rimane nel bicchiere, grazie alla pressione atmosferica che preme sul foglio di carta. Quasi obbligatorio svolgere quest'esperienza ogni anno in laboratorio di Fisica!
	Un'altra esperienza "casalinga" per la dimostrazione della pressione atmosferica è quella ritratta in queste due fotografie. Occorre prendere una candela e fissare mediante cera colata sul fondo di una vaschetta, in cui vengono versati alcuni centimetri d'acqua. Si prende poi un becker e lo si capovolge sulla candela, che subito si spegne. E allora...
	...si osserva con sorpresa che l'acqua viene spinta dentro il becker. Questo avviene non perchè la candela consuma l'ossigeno creando una depressione, come molti credono, ma perchè l'anidride carbonica prodotta dalla combustione è solubile in acqua, quindi vi si discioglie, diminuendo la pressione interna al becker. Ciò può essere facilmente dimostrato utilizzando un rivelatore di pH, perchè l'anidride carbonica renderà l'acqua leggermente acida. Un'esperienza davvero di grande effetto.
	Un altro strumento fondamentale per verificare l'esistenza della pressione atmosferica è il baroscopio, (dal greco "mostra la pressione"), anche se il suo uso è più delicato di quello del barometro. Si tratta di una piccola bilancia, un braccio della quale è sostituito da un palloncino di vetro nel quale è praticato il vuoto. In pratica il palloncino, oltre al proprio peso, avverte anche la spinta idrostatica dell'aria, che è pari al peso di un volume d'aria uguale a quello del palloncino. Il peso a destra dunque è pari alla differenza tra il peso del palloncino stesso e la spinta idrostatica da esso subita.
	Ed ecco il baroscopio in opera: è posto sotto la campana di vetro e la pompa a vuoto, visibile sulla destra, sta estraendo tutta l'aria. In tal modo è facilissimo verificare che la bilancia si allontana dall'equilibrio e pende dalla parte del palloncino. Questo perchè viene a mancare la spinta idrostatica dell'aria che contribuiva a mantenere in equilibrio lo strumento!! Il successo è assicurato anche se, con le pompe a nostra disposizione, si ottiene soltanto una pendenza piuttosto lieve. Cliccando qui potrete scaricare un breve filmato di questa simpatica esperienza.
	Lo scatto rappresenta una copia in scala ridotta (ma perfettamente funzionante) dei celebri emisferi di Magdeburgo, così detti perché Otto von Guericke (1602-1686) li usò per dimostrare l'esistenza della pressione atmosferica ai Grandi Elettori del Sacro Romano Impero riuniti alla Dieta di Magdeburgo. Dopo aver estratto l'aria dall'interno di essi, un tiro ad otto cavalli non riusciva a separarli! Questi esemplari sono sufficienti affinché una persona da sola non riesca a staccarli l'uno dall'altro.
	Ecco i due emisferi all'opera, grazie alla collaborazione di un mia collega. Dentro di essi è stato praticato il vuoto mediante l'apposita pompa, quindi il rubinetto è stato chiuso (come si vede, i bordi dei due emisferi sono unti di grasso affinché aderiscano meglio e l'aria non filtri). La collega, da sola, non è in grado di separarli; ci sono voluti almeno due studenti robusti per riuscire a farlo. Ad impedire il distacco degli emisferi è la pressione atmosferica esterna, non più controbilanciata da quella interna.
	Quello illustrato in questa foto composita è un altro facile esperimento che dimostra l'esistenza della pressione dell'aria. Si versa dell'alcool da cucina in un barattolo di vetro, lo si chiude con pellicola trasparente avendo cura che sia ben tesa, poi lo si immerge in una bacinella di acqua calda. Il calore fa evaporare l'alcool e la pellicola si gonfia verso l'alto (in alto a destra), ma poi si raffredda, la pressione interna diminuisce e quella atmosferica (in basso a destra) schiaccia la pellicola verso il basso!
	Un'altra prova dell'esistenza della pressione atmosferica è fornita da questa immagine, scattata in una cameretta d'ospedale. Ad un paziente è stata collegata una fleboclisi per iniettargli un farmaco via endovena; quando la bottiglia del farmaco era piena aveva la consueta forma ma, man mano che il liquido entra nel corpo, la bottiglia si schiaccia. Infatti il farmaco defluisce e, siccome nella bottiglia non v'è aria onde evitare la formazione di emboli, la pressione dell'atmosfera comprime la bottiglia, così come comprimeva la pellicola della foto soprastante!
	Naturalmente, parlando di pressione atmosferica, non può mancare una foto ad alta risoluzione di un barometro aneroide. Non si tratta di un barometro a mercurio come quello di Torricelli, ma di un "barometro metallico": esso contiene una scatoletta circolare (visibile nella foto sotto il quadrante) in cui è praticato il vuoto spinto e chiusa con una lamina metallica, a sua volta collegata alla lancetta. Al variare della pressione esterna la lamina si schiaccia o si rilassa, facendo ruotare la lancetta. Alta pressione significa bel tempo, bassa pressione significa la formazione di perturbazioni atmosferiche.
	Ed ecco il vero barometro a Torricelli, composto da una vaschetta piena di mercurio (in basso) in cui è immerso un tubicino alto un metro che viene riempito a sua volta di mercurio e poi capovolto nella vaschetta. Evangelista Torricelli (1608-1647), discepolo di Galileo Galilei, osservò che il mercurio nel tubicino scende fino ad un'altezza di 760 mm al livello del mare, ad un'altezza inferiore a quote più elevate, e concluse che la colonnina di mercurio è tenuta in equilibrio dalla pressione atmosferica, che infatti decresce al crescere della quota. È questa a stabilire i limiti entro cui può funzionare una pompa.
	Si dice invece manometro (dal greco manos, "rarefatto") lo strumento deputato alla misura della pressione di un fluido (un liquido o un gas) diverso dall'aria atmosferica, ad es. l'aria contenuta negli pneumatici di un'automobile o l'olio contenuto nei suoi freni. Quello qui illustrato è il più antico tipo di manometro della storia, il manometro a mercurio. Infilando il tubo di gomma in un fluido, la pressione fa abbassare il livello del mercurio nel tubo di destra e lo fa alzare in quello di sinistra; il dislivello, per mezzo della legge di Stevin, permette di ricavare la pressione. Purtroppo il ramo di sinistra è aperto e dunque lo strumento va usato con attenzione per evitare di rovesciare il mercurio. Questo modello sarà applicato nell'esperienza di Stevin.
	Ed ecco invece un manometro metallico Di questi strumenti si è già parlato abbondantemente nell'Armadio Virtuale dedicato agli Strumenti di Misura, ma anche in questo Armadio giova inserirne uno per ragioni di completezza. Il recipiente del quale si deve misurare la pressione è collegato tramite un tubo ad una membrana metallica che si deforma tanto più quanto maggiore è la pressione del fluido; la deformazione produce il movimento della lancetta sulla scala graduata, tarata direttamente in bar (1 bar = 10.000 Pascal). Il modello fotografato è ancora perfettamente funzionante.
	Ed ecco un microdeprimometro, donato a questo Laboratorio Virtuale dalla mia collega prof.ssa Maria Elena Tarantino. Il deprimometro è uno strumento utilizzato per rilevare il tiraggio delle canne fumarie, il cui principio di funzionamento si basa su due misurazioni di pressione mediante manometri, quella esterna e quella interna alla canna fumaria. La differenza delle due pressioni fornisce il tiraggio della stessa.
	Un dispositivo molto semplice per verificare il principio di Pascal: la pressione si esercita uniformemente in tutte le direzioni (isotropia). Riempiendo d'acqua la provetta e spingendo lo stantuffo, i getti d'acqua sono uguali in tutte le direzioni.
	Il Principio di Pascal è anche alla base del funzionamento di questa siringa per uso clinico: si preme sul fluido contenuto nella siringa tramite lo stantuffo di plastica, la pressione è trasmessa dal fluido in tutte le direzioni, e così il contenuto della siringa può venire espulso dal sottile ugello che termina nell'ago, ed iniettato dentro il corpo umano.
	Il principio di Pascal può essere abilmente sfruttato nel martinetto idraulico, di cui qui si vede un esemplare fotografato dall' autore di questo sito, ed utilizzato per muovere il braccio meccanico di una ruspa. Il tubo scuro fotografato a sinistra pompa olio dentro il martinetto; siccome la pressione si distribuisce uniformemente in tutte le direzioni, è sufficiente una pressione non elevatissima dell'olio per esercitare una forza anche notevole sullo stantuffo del martinetto, e permettergli così di scavare grandi quantità di terriccio.
	Lo stesso principio viene sfruttato per sollevare gli automezzi da riparare attraverso il martinetto idraulico che qui vediamo all'opera in un'officina meccanica. Premendo su un'opportuna leva (nei modelli moderni si sfrutta invece una pompa) viene compresso l'olio contenuto in un serbatoio, che a sua volta spinge verso l'alto quattro stantuffi, i quali reggono la piattaforma su cui è posta l'automobile da riparare. In tal modo, anche con una forza esigua è possibile sollevare un peso enorme, come quello di un'automobile!
	La figura illustra il classico esperimento dei vasi comunicanti, diretta conseguenza della legge di Stevin, la quale afferma che la pressione dovuta ad una colonna di fluido dipende dalla profondità e non dalla sezione del recipiente o dalla sua forma. E quest'esperienza, facilmente comprensibile persino per un alunno delle scuole elementari, lo illustra a perfezione: il livello dell'acqua è lo stesso in tutti e cinque i rami!
	Quello in figura è un bellissimo modello di acquedotto romano realizzato dagli studenti del mio Liceo. Il primo acquedotto di questo tipo fu costruito nel VII secolo a.C. dagli Assiri per rifornire di acqua la loro capitale Ninive, ma furono i Romani ad eccellere nell'arte del trasporto dell'acqua: Roma era servita da 11 acquedotti per una lunghezza complessiva di circa 350 km. L'acquedotto romano a Ponte del Gard (Provenza) ha un dislivello di soli 34 cm per km, scendendo di soli 17 m nella sua intera lunghezza di 50 km. A volte, quando si incontravano lungo il percorso depressioni maggiori di 50 m, venivano utilizzati i sifoni inversi, condotte a gravità in uso anche ai giorni nostri per gli impianti idrici e fognari.
	Qui vedete ritratto un metodo per travasare il vino, cioè per trasferirlo dalla damigiana alla bottiglia. Si immerge per circa venti centimetri un’estremità di un tubo di gomma nel liquido della damigiana; l’altra estremità la si porta alla bocca e si aspira. In questo modo si costringe il liquido a penetrare nel tubo per effetto della diminuzione della pressione interna, che risulterà inferiore a quella atmosferica esterna. Una volta estratto il liquido dal contenitore, l’aspirazione provocherà la spinta verso l’altro recipiente. Per evitare che la corsa rallenti, non appena si avverte l’arrivo del liquido alle labbra bisogna immergere rapidamente il tubo nella bottiglia!
	In questa foto, scattata il 22/03/2005 dai miei studenti Andrea Zaro e Simone Zendali (II A cl. a.s. 2004/05) mostra il becker da 4 litri e la sonda manometrica con la quale è possibile eseguire la verifica sperimentale della legge di Stevin. La sonda è costituita da un pescante, che può essere abbassato grazie ad una vite di regolazione, e da un manometro, nel quale si versa acqua per mezzo di un imbutino. Mano a mano che il pescante viene abbassato aumenta il dislivello tra i due bracci del manometro, ed è possibile verificare in modo semplice la diretta proporzionalità tra profondità e pressione dell'acqua.
	Altra interessantissima esperienza di idrostatica è la verifica del Principio di Archimede mediante l'uso della bilancia idrostatica. Si tratta, come si vede, di una normalissima bilancia, nella quale un piatto è sostituito da una gancio cui è appeso un cilindretto di plastica. Dopo aver equilibrato quest'ultimo sulla bilancia, lo si immerge in un becker pieno d'acqua, e si verifica che la bilancia torna in equilibrio solo dopo aver posto sull'altro piatto un cilindretto di ugual volume, cavo e pieno d'acqua. La spinta del fluido è dunque pari al peso del volume di liquido spostato!!
	Quella qui illustrata è la celeberrima esperienza del diavoletto di Cartesio, così detta dal suo ideatore René Descartes (1596-1650). Si tratta di un "diavoletto" cavo di vetro, contenente aria ed acqua ed immerso in un cilindro di vetro chiuso da una membrana elastica. Esercitando con il pollice una pressione sulla membrana, il diavoletto affonda, e diminuendo la pressione esso risale. Infatti, premendo sulla membrana, questa trasmette la pressione sull'aria, ed essa a sua volta all'acqua, che è forzata ad entrare nel diavoletto, cosicché l'aria in esso contenuta è compressa. Divenendo più pesante, il diavoletto affonda; togliendo il dito, l'aria riprende il volume originario, espelle l'acqua e il diavoletto risale. Questo è il principio su cui si basa la vescica natatoria dei pesci. Ecco un filmato che illustra questa spettacolare esperienza!
	Questa foto, scattata dall'amico Sandro Degiani durante un suo viaggio in Tunisia nell'estate 2007, ci è utile per illustrare il principio di galleggiamento delle navi. Il legno di cui è fatta questa nave ha una densità assai maggiore di quella dell'acqua, ma la forma dello scafo è tale che esso sposta una quantità d'acqua più pesante di esso, e questo le consente di galleggiare e di navigare tranquillamente!
	Una delle glorie del Museo Nazionale della Scienza e della Tecnica di Milano è il sottomarino Enrico Toti, qui fotografato dall'autore di questo sito. Terminato il servizio attivo il 30 giugno 1999, dopo un viaggio lungo e avventuroso il 14 agosto 2005 raggiunse il cortile del Museo, dov'è conservato tuttora. Un sottomarino può immergersi od emergere proprio grazie al Principio di Archimede, riempiendo o svuotando d'acqua le casse di zavorra.
	Questo esemplare di mongolfiera è stato fotografato da Gaia Macchi al Museo Nazionale della Scienza e della Tecnica di Milano. Inventata dai fratelli Joseph-Michel (1740-1810) e Jacques-Etienne Montgolfier (1745-1799), essa consentì all'uomo di staccarsi dal suolo per la prima volta. Si tratta in buona sostanza di un pallone riempito d'aria calda grazie ad un semplice bruciatore posto subito al di sotto dell'involucro; grazie al principio di Archimede, esso "galleggia" sull'aria fredda circostante. In realtà quello presente al Museo è solo un modellino, essendo l'involucro troppo piccolo per sostenere il peso della navicella.
	Uno strumento classico: un pallone di vetro utilizzato per pesare l'aria. In pratica lo si pesa, poi si estrae tutta l'aria con una pompa a vuoto, si pesa nuovamente e la differenza costituisce il peso dell'aria all'interno. In realtà non si pesa affatto l'aria ma la spinta idrostatica che il pallone sente, immerso nell'atmosfera, dopo essere stato svuotato, proprio come lo scafo di una nave, internamente cavo, avverte la spinta dell'acqua che lo fa galleggiare. Proprio questa spinta aveva fatto erroneamente concludere ad Aristotele che l'aria non pesa!
	Quello qui fotografato è un esemplare pressoché storico di pompa ad aria, utilizzato per gonfiare pneumatici di bicicletta. Si tratta di una pompa ad aria detta « aspirante-premente », funzionante ad azionamento manuale, che sfrutta un semplice sistema di valvole di non ritorno. Quando si solleva lo stantuffo con due mani, si chiude la valvola di mandata, che mette in diretta comunicazione la camera d'aria con il tubo collegato allo pneumatico, mentre si apre quella che aspira aria dall'esterno; quando lo stantuffo è abbassato, è quest'ultima a chiudersi e la prima ad aprirsi, cosicché l'aria viene spinta nella gomma.
	Un apparecchio insostituibile per le esperienze di Fisica (soprattutto per quelle di Termodinamica) è la pompa a vuoto, in grado di aspirare gran parte dell'aria da sotto una campana di vetro o da altri dispositivi, come quello fotografato subito sotto. Il modello raffigurato è un po' datato ma tuttora perfettamente funzionante. Si noti che essa ha esattamente lo scopo opposto della pompa a mano precedente; quella inviava l'aria dentro una cavità, questa invece ha lo scopo di pomparla fuori!
	Dopo l'idrostatica, l'idrodinamica. Questo strumento è una semplice pompa idraulica, del tipo utilizzato dentro le comuni lavatrici, smontato dal mio allievo Davide de Alberti (III B cl. 2005/06) e portato in classe a scopo dimostrativo. In basso a sinistra si scorge la girante della pompa, mentre nel pezzo smontato a destra si possono vedere l'ugello di afflusso e quello di deflusso dell'acqua.
	Questo aspiratore chirurgico, fotografato in una stanza d'ospedale dietro permesso dei medici curanti, non è altro che un'applicazione per uso medico delle pompe sopra descritte, necessario ad esempio per aspirare liquidi organici dalla gola di un paziente, che altrimenti potrebbe soffocare. La pressione di aspirazione è regolabile tramite un'apposita manopola, visibile sulla destra del quadro comandi, mentre un vuotometro (cioè un manometro) indica il valore raggiunto da tale pressione. Si noti che i suoi valori sono negativi, come comporta il fatto che la macchina funzioni solo in aspirazione (si arriva fino a - 1 bar). Naturalmente lo strumento è dotato di filtro antibatterico monouso.
	Altre due pompe, molto più complesse e sofisticate della precedente, e tuttora in funzione, comandano l'impianto termico della casa dell'autore di questo sito. Si noti che la pompa, necessaria alla circolazione dell'acqua calda nell'impianto dei caloriferi, è doppia, in modo da poter periodicamente spegnere l'una e far funzionare l'altra, onde ridurre i rischi di usura. Se la pressione del liquido diventa localmente inferiore alla sua tensione di vapore, la pompa subisce il fenomeno della cavitazione, cioè nella colonna d'acqua si formano cavità piene d'aria, che possono danneggiare gravemente lo strumento.
	Un componente essenziale di ogni impianto idraulico è la camera di compensazione o polmone. In pratica è uno spazio chiuso in cui si produce un battente d'acqua sovrastato da aria (cioè l'acqua non lo riempie completamente e sopra il pelo dell'acqua c'è una bolla d'aria); le variazioni di pressione in tal modo non fanno scoppiare i tubi, ma vengono compensate dall'aumento o dalla diminuzione del livello dell'acqua nel polmone. Accanto ad esso si vede un manometro.
	Anche gli impianti idrici più grandi hanno una camera di compensazione: è il caso dell'acquedotto comunale di Lonate Pozzolo (VA), il comune di residenza di chi scrive. Esso era utilizzato, prima dell'avvento delle grandi pompe meccaniche, per permettere all'acqua di arrivare fino ai rubinetti dei piani più alti degli edifici, in base al principio dei vasi comunicanti (vedi). La torre in questione è alta 40 metri, e sopravanza gli alti abeti circostanti.
	In questa foto mi trovo al Museo Nazionale della Scienza e della Tecnica di Milano il 26/02/2005, e la mia studentessa Gaia Macchi (III B cl. a.s. 2004/05) mi ha fotografato accanto alla girante di una turbina Francis, nella sezione del Museo dedicata alle fonti di energia. Ci sono tre tipi di turbine ad acqua: Kaplan, per bassi dislivelli; Francis, per dislivelli intermedi; e Pelton (o "a cucchiai") per dislivelli molto grandi. Queste turbine sono fondamentali negli impianti idroelettrici per la produzione di energia, come quello che viene illustrato qui sotto.
	Dopo la turbina Francis, ecco una turbina Pelton, dalle tipiche pale a forma di cucchiaio, fotografata dall'autore di questo sito al Museo Nazionale della Scienza e della Tecnica di Milano il 23/05/2013. Essa è così detta perchè fu inventata nel 1879 dal carpentiere Lester Allan Pelton, mentre lavorava in California, e risulta la turbina con rendimento più elevato. È utilizzata per grandi salti (di solito tra i 300 e i 1400 m) e piccole portate (inferiori a 50 m³/s). Il braccio della guida del Museo che si intravede aiuta a stimarne le reali dimensioni.
	Volete vedere una turbina Pelton in situ, quindi non in un Museo ma in una centrale idroelettrica? Eccovi accontentati prontamente. La foto mi è stata inviata da Giuseppe Biundo, ingegnere laureatosi a Catania, che ha studiato le antiche centrali idroelettriche del Parco delle Madonie, ed appartiene ad una centrale idroelettrica in contrada Paratore (PA), entrata in funzione nel dopoguerra.
	Questo collage di immagini, dovute ancora all'amico Giuseppe Biundo, ci mostra gli antenati delle moderne centrali a turbine: antichi mulini idraulici fotografati sulle Madonie, che sfruttavano il « carbone bianco » generato dalle abbondanti acque di pioggia e dallo scioglimento delle nevi che alimentano i fiumi Imera Settentrionale, Roccella, Pollina e Imera Meridionale: lungo di essi già nell'XI secolo sono documentate le "flomarie molendorum madonite", frutto del patrimonio di conoscenze che gli arabi ebbero dell’acqua. Una ruota idraulica del tipo di quelle qui illustrate poteva produrre una quantità di farina pari a quella macinata da 40 uomini con macine a mano. Si osservino in particolare gli straordinari apparati molitori qui rappresentati.
	Sempre grazie alla generosità di Giuseppe Biundo, che mi ha fornito queste sue fotografie, posso pubblicare anche un'immagine composita che illustra quanto resta di una centrale idroelettrica costruita nel 1908 a Petralia Sottana (PA) in località Catarratte, nel Parco delle Madonie. In alto a sinistra si vedono le condotte forzate, che portano l'acqua alle turbine coprendo un dislivello di 160 m; in alto a destra c'è il quadro di controllo e misura; in basso a sinistra i gruppi turbina-generatore; in basso a destra le vasche di carico. La centrale produceva corrente elettrica alternata trifase, e rimase in esercizio sino al 1976.
	Quella che vedete ritratta in questa foto composita è la fontana basculante realizzata dallo studente Jacopo Piccoli della 2 B a.s. 2014/15. Si tratta in effetti di un'applicazione dell'equilibrio del corpo rigido: dal secchio appeso al muro gocciola acqua nella canna di bambù libera di ruotare attorno al suo centro; la canna vuota ruota con la parte aperta verso l'alto, mentre la canna piena d'acqua ruota nel senso opposto, svuotandosi, perchè la somma dei momenti ha il segno positivo con la canna vuota, e il segno opposto con la canna piena. Davvero un ottimo lavoro!
	Questa foto, cortesemente speditami dalla collega Antonietta Nisi, rappresenta un ariete idraulico. Che cos'è? Se in un condotto percorso da acqua viene bruscamente arrestato il flusso del liquido, la velocità crolla a zero, ma l'energia cinetica della massa liquida non si annulla, ed aumenta notevolmente la pressione dinamica del liquido contro le pareti. Di conseguenza il liquido rifluisce verso il serbatoio dal quale proviene e si innalza al disopra del livello originario. Per via dell'improvviso aumento della pressione dinamica si sente, alla chiusura del condotto, un colpo secco detto colpo d'ariete. Si riempie l’apparecchio di acqua versandola nell’imbuto, si preme la valvola in basso, l’acqua fluisce e raggiunge una velocità costante; si lascia allora la valvola, che si chiude: contemporaneamente l'acqua sale nel tubo piezometrico e una certa quantità si riversa nell’imbuto.
	L'esperienza qui illustrata, e realizzata dal prof. Giovanni Brazzelli (del quale si vede la mano), è la misura della viscosità di un fluido attraverso la caduta di un grave. A sinistra si vede il materiale necessario per l'esperienza: un cilindro graduato, del fluido viscoso (in questo caso del bagnoschiuma), delle palline di metallo di cui si misura la massa con la bilancia elettronica ed il diametro mediante il calibro, in modo da determinarne la densità. Anche la densità del fluido viscoso è determinata pesando il cilindro graduato, sottraendo la tara e dividendo per il volume. Come si vede a destra, il prof. Brazzelli lascia cadere la sferetta dentro il fluido viscoso (per farla cadere a partire dal livello del fluido si può usare una pinzetta, mentre la calamita serve per recuperare la pallina metallica al termine dell'esperienza)...
	...Intanto un altro studente misura il tempo necessario alla caduta, fissando un livello di partenza e uno di arrivo; per esempio, se il cilindro è tarato da 0 a 250 ml, si scelgono 200 ml come partenza e 50 ml come arrivo, in modo che la velocità di caduta del grave nel fluido viscoso abbia il tempo di andare a regime. Infatti l'attrito viscoso del fluido sulla sferetta fa sì che essa cada con velocità costante, e non di moto accelerato, come mostra questo breve filmato digitale. Determinando la velocità di caduta (dividendo lo spazio per il tempo) si risale con una nota formula alla viscosità misurata in Poise (0,1 Pascal per secondo). Se il diametro della sferetta diminuisce, diminuisce anche la velocità di caduta, come mostra questo secondo filmato.
	Si dice fluido non newtoniano un fluido la cui viscosità varia a seconda dello sforzo di taglio che viene applicato ad esso. Di conseguenza, i fluidi non newtoniani non hanno un valore definito di viscosità. Se la viscosità aumenta all'aumentare della velocità di deformazione, si parla di fluidi dilatanti. Un semplice esempio di fluido non newtoniano dilatante può essere realizzato miscelando acqua e amido di mais. L'applicazione di una forza, come ad esempio fanno queste ragazze del mio Liceo calpestandolo energicamente con i piedi, induce il fluido a comportarsi come un solido più che come un liquido. Applicando una forza sufficiente con i piedi, si può letteralmente camminare sopra un tale liquido.
	Qui vediamo un divertente giocattolo che ha più di una ricaduta didattica. Esso infatti consiste in una ventola (dotata di Led che si accende quando la ventola è in funzione) che soffia verso l'alto un flusso d'aria in grado di tenere in equilibrio a mezz'aria una pallina di plastica (ecco un breve filmato digitale che ne illustra il funzionamento). La portata di un flusso di fluido può essere una portata in massa (la massa di fluido che attraversa la sezione del flusso nell'unità di tempo), misurata in Kg/s, oppure la portata in volume (il volume di fluido che attraversa la sezione del flusso nell'unità di tempo), misurata in metri cubi al secondo e pari anche al prodotto della velocità del flusso per l'area della sezione.
	Questo è un paracadute dispiegato nel corso di una mostra tenutasi presso il mio Liceo e dedicata al 105° anniversario (1909-2014) della fondazione dell'Aeronautica Militare Italiana. Il paracadute (nella parte inferiore della foto se ne vede uno ripiegato di tipo ventrale) è un deceleratore aerodinamico, in grado di imprimere una accelerazione contraria rispetto all'attrazione gravitazionale a un corpo sottoposto a caduta libera nell'atmosfera, del quale rallenta la discesa verso il suolo. Per lo più si crede che esso trasformi il moto rettilineo uniformemente accelerato in uno rettilineo uniforme; in realtà esso trasforma un moto uniforme ad alta velocità in uno a velocità assai più bassa, consentendo l'atterraggio!
	È giusto chiudere questo Armadio Virtuale con un cenno all'aeronautica. Questa foto è stata scattata dal sottoscritto nei pressi di Malpensa 2000 e ritrae un aereo in fase di atterraggio. L'ala è sagomata in modo che il flusso dell'aria sopra di essa è diverso da quello sotto di essa; in base al Teorema di Bernoulli, le diverse velocità producono una diversa pressione, e ciò si traduce in una spinta effettiva verso l'alto dell'ala, chiamata portanza. Se l'aereo rallenta la portanza cessa ed esso cade in stallo.
	Quello che qui vedete rappresentato è un modellino (funzionante!) di Caudron G III, un velivolo francese costruito nel 1911 ed utilizzato durante la Grande Guerra sul Fronte Occidentale. Esso aveva un peso complessivo di soli 736 Kg, perchè le ali erano di stoffa cucita; poteva viaggiare a 125 Km/h (una velocità ridicola, se confrontata a quella dei bolidi di oggigiorno!) e una quota di 3000 metri. L'autonomia era di quattro ore, poteva ospitare due persone e aveva la funzione di ricognitore. Il 7 marzo 1913 esso compì il primo decollo dal ponte di una nave francese!
	Qui vediamo fotografato il seggiolino eiettabile di un velivolo F104. Il suo scopo è quello di garantire la sopravvivenza del pilota quando il velivolo non è più governabile, e dunque bisogna necessariamente lanciarsi al di fuori dell'abitacolo. Nella maggior parte dei modelli, il sedile viene espulso dall'aereo grazie a motori a razzo, e dopo pochi secondi viene si apre automaticamente un paracadute. Per lanciarsi, il pilota deve tirare uno degli anelli che si trovano tra le sue gambe o sopra la testa. Il seggiolino eiettabile fu brevettato in Germania nel 1939; prima di allora l'unico modo per salvarsi da un aereo che precipitava era saltare fuori attraverso il tettuccio: operazione però spesso molto difficile.
	Dopo l'aereo, l'elicottero. Questo esemplare di NH90, realizzato dalle NHIndustries ed ampiamente utilizzato dall'esercito italiano, mostra un classico esempio di ala rotante, in cui la portanza è data non dall'alta velocità del mezzo, ma dalla rapidissima rotazione delle due pale. In tal modo l'elicottero può sollevarsi dal suolo praticamente da fermo. L'elica di coda serve ad impedire che le pale restino ferme e ruoti invece l'elicottero.
	Quella che potete osservare in questa fotografia è l'elica posteriore realizzata in fibra di carbonio di un deltaplano a motore mostratomi dal mio studente Riccardo Dal Cortivo (3 E a.s. 2020/21), che la possiede perchè suo fratello lavora in una azienda che le fabbrica. Si vedono entrambi i lati della pala dell'elica, i quali mostrano il diverso profilo alare necessario per ottenere una differenza di velocità e di conseguenza una portanza in grado di spingere l'ultraleggero. Nel riquadro si vede chiaramente anche la sezione dell'elica con la caratteristica forma.
	In questa rassegna non poteva certo mancare la foto di un drone, progettato e realizzato dal mio brillante studente Domenico Maisto, laureatosi nel 2018 in Ingegneria Fisica. L'ottimista Domenico mi ha scritto: « Appena sentirà uno schianto, vorrà dire che lo avrò collaudato! » Io però sono convinto che grazie alle sue quattro eliche volerà benissimo!
	Chiudiamo questa galleria con quello che fu il sogno di Leonardo da Vinci: trasformare in realtà il volo umano. Questa foto è stata scattata il 23/05/2013 presso il Museo Nazionale della Scienza e della Tecnica di Milano, che è intitolato proprio a Leonardo. A differenza dei moderni parapendio, questo dispositivo è stato pensato ad ali battenti; l'aeronauta avrebbe dovuto sedersi sopra di esse nel sedile che si vede al centro, ed azionarle con braccia e gambe. Non funzionò ma, come diceva Antoine de Saint-Exupery, sarebbe stata una follia abbandonare tutti i sogni perché uno di loro non si è realizzato!
Cliccate qui per scaricare alcune schede per realizzare molte delle esperienze di questa galleria
Queste immagini possono essere liberamente utilizzate da chiunque, purché se ne citi la fonte

Torna alla galleria immagini del mio sito