Home | Eventi | Protagonisti |  Glossario | Bibliografia | Sitografia | Scrivimi

Dicesi laplaciano l'operatore differenziale introdotto da Laplace e definito simbolicamente dalla relazione:

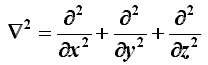
esso rappresenta la divergenza di un gradiente. L'equazione detta “di Laplace” per una funzione U(x, y, z), si scrive U = 0. Le soluzioni di tale equazione con derivate seconde continue prendono il nome di funzioni armoniche. L'equazione di Laplace permette per esempio di determinare le posizioni di una membrana elastica indefinita non soggetta a forze.

Dicesi invece trasformata di Laplace il funzionale lineare associato a una funzione F(t) della variabile reale t simboleggiato da Lz [ F(t) ], definito dalla relazione seguente:

dove z è un numero complesso. L'integrale che compare in tale relazione è detto integrale di Laplace; la funzione F(t) è nota come funzione generatrice di Lz. La classe di funzioni rappresentabili con un integrale di Laplace almeno in una regione del piano complesso z è molto ampia; inoltre la trasformata di Laplace gode di notevoli proprietà che la rendono particolarmente utile in diversi rami non solo della matematica pura, ma soprattutto dell'elettronica.