![]()
L'esercizio numero 5 non richiede solo un calcolo numerico, ma una vera e propria dimostrazione, analoga a quella del paragrafo A.2, dunque è riservato ai solutori più che abili. Come nel caso dell'Equazione di Fourier, è necessario ricorrere all'Analisi Matematica: lo scopo è quello di determinare l'andamento della temperatura in un corpo solido omogeneo di forma allungata, di cui un estremo viene permanentemente tenuto ad una temperatura prefissata T0, mentre il resto della superficie emette calore per convezione in un ambiente fluido tenuto a temperatura costante Ta. Il corpo solido, nel caso dell'esercizio proposto, è rappresentato da una sbarra metallica ad asse rettilineo e con sezione costante, di superficie S e perimetro P; le dimensioni della sezione sono molto ridotte rispetto alla lunghezza dell'asta; per questo motivo tutti i punti della sezione si possono supporre alla stessa temperatura T, che di conseguenza è funzione della sola distanza x dall'estremità tenuta alla temperatura T0. Supponiamo inoltre che il coefficiente di conducibilità λ del materiale di cui la sbarra è costituita sia costante, e non vari né con la posizione né con la temperatura; infine, supponiamo che il coefficiente di convezione h tra la sbarra e l'ambiente sia costante ed indipendente dalla temperatura. Il tutto può essere rappresentato in un diagramma come questo:
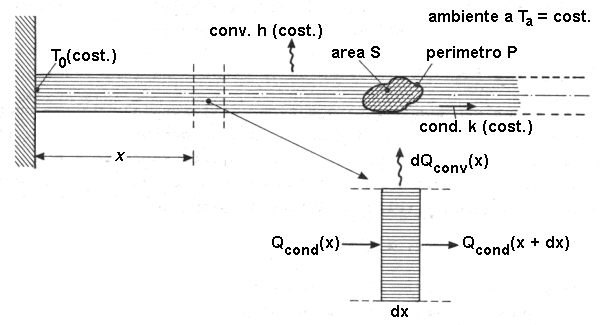
A questo punto, impostiamo un'equazione differenziale per risolvere il problema della trasmissione del calore; tale equazione sarà valida solo in regime stazionario. Consideriamo la generica sezione a distanza x dall'estremità della sbarra a temperatura T0 e quella a distanza x + dx da essa. Per l'elementino di sbarra di spessore dx compreso tra tali sezioni, la differenza fra la potenza termica entrante e quella uscente per conduzione deve essere uguale alla potenza termica uscente per convezione dalla periferia dell'elemento. In simboli:
![]()
La conduzione è regolata dall'equazione (A.1), da noi studiata nel § A.1. Scriviamola in termini differenziali:
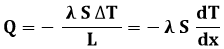
Anche la (A.10), scritta nel § A.3, può essere scritta in termini differenziali:
![]()
perchè l'area della superficie laterale della sbarra attraverso cui avviene lo scambio convettivo è pari al perimetro della sezione per la lunghezza dell'elemento considerato. Sostituiamo le precedenti nel bilancio termico ed avremo:

E per le proprietà delle derivate:

Di conseguenza:
![]()
Otteniamo così la seguente equazione differenziale del secondo ordine:
![]()
Indicando con θ = T – Ta la differenza tra la temperatura della sbarra e quella dell'ambiente circostante, e ponendo:
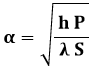
la nostra equazione differenziale può essere riscritta:
![]()
Questa equazione è ben nota a chi ha studiato l'Analisi Matematica, e il suo integrale generale è:
![]()
dove A e B sono costanti da determinare mediante le condizioni al contorno. L'esercizio in questione ci chiede di risolvere questa equazione differenziale nel caso particolare (e più semplice) in cui la sbarra è lunghissima rispetto alle sue dimensioni trasversali, e quindi idealmente infinita. In tal caso, la temperatura alla sua estremità diventa pari a quella Ta dell'ambiente, e quindi le condizioni al contorno si riducono alle seguenti:
![]()
Sostituendo nell'espressione di θ (x) sopra trovata si ha:
![]()
Ma la seconda è possibile solo se A = 0, perchè altrimenti questo addendo diverge all'infinito. Sostituendola nella prima si ricava B = θ0. Quindi l'unica soluzione compatibile con le condizioni al contorno è la seguente:
![]()
Rappresentando graficamente questa soluzione in coordinate cartesiane, troviamo:

Il parametro α è detto smorzamento rispetto alla coordinata x, ed ha le dimensioni dell'inverso di una lunghezza. Lo smorzamento evidenzia con quale rapidità la temperatura tende all'asintoto T = Ta: maggiore è α, più rapidamente la temperatura si avvicina a Ta. Si osservi che, a parità di materiale (λ) e di forma della sbarra (P / S), lo smorzamento α aumenta con h. Esso è dunque molto più elevato in acqua che in aria, così come è più elevato in aria in movimento che in aria stagnante. Invece, a parità di forma della sbarra (P / S) e di coefficiente di convezione (h), lo smorzamento α cresce al diminuire di λ; ad esempio, esso è molto più elevato con il ferro che con l'alluminio, con l'alluminio che non con il rame. A parità di materiale (λ) e di coefficiente di convezione (h), lo smorzamento α aumenta all'aumentare del rapporto P / S, e conseguentemente a parità anche di S aumenta all'aumentare di P. Ora, a parità di sezione S, si può dimostrare che il perimetro P minimo corrisponde alla sezione circolare, che logicamente ha lo smorzamento α minimo; se invece la sezione ha una forma frastagliata, cioè è dotata di alette, il rapporto aumenterebbe incredibilmente, e con esso aumenterebbe α. È questo il famoso "effetto aletta", fondamentale per il raffreddamento di motori e componenti meccanici, misurato dal parametro P / S. Ecco ad esempio le alette di cui sono dotati dei componenti hardware di alluminio, studiati per raffreddare le schede madri dei Pc domestici (da questo sito):

Dopo aver trovato il profilo di temperatura, vale la pena di trovare anche la potenza termica dissipata a una distanza x dalla parete:
![]()
Alla base della sbarra (per x = 0), si ha:
![]()
Confrontiamo questa potenza con quella che la superficie S, alla temperatura T0, disperderebbe per convezione nell'ambiente a temperatura Ta (come se la sbarra non ci fosse):
![]()
Si introduce il coefficiente di amplificazione termica β della sbarra, un numero adimensionale definito come il rapporto tra la potenza termica alla base della sbarra e quella che si avrebbe senza sbarra:

Il coefficiente di amplificazione β della sbarra può essere maggiore, uguale o minore di uno. L'effetto aletta per un materiale metallico che disperde calore in un fluido può far arrivare β a valori molto elevati, superiori a 1000!
Ora torniamo al nostro esercizio numerico. Nel nostro caso, la sezione è rettangolare e quindi S = 3 x 0,5 cm = 1,5 cm2, mentre P = 2 ( 3 + 0,5 ) = 7 cm. Di conseguenza, P / S = 4,67 mentre lo smorzamento α vale 4,91 m–1. Siccome θ0 = 300° – 20° = 280°, la formula risolutiva è:
![]()
Sostituendo in essa i tre valori di x riportati nel testo dell'esercizio si trova:
T ( x = 5 cm ) = 219° + 20° = 239°
T ( x = 50 cm ) = 24° + 20° = 44°
T ( x = 100 cm ) = 2,1° + 20° = 22,1°
La risposta esatta perciò è la numero 2. Si osservi che la numero 4 è sbagliata perchè si tratta dei valori di θ, non di T: ad essi bisogna sommare i 20° dell'ambiente per trovare gli effettivi valori di temperatura cercati. Per curiosità, il coefficiente di amplificazione nel nostro caso vale circa β = 95. Se invece che 3 x 0,5 cm la sbarra in questione misurasse 30 x 0,05 cm, la sezione S sarebbe la stessa, ma il perimetro P salirebbe a 60,1 cm, per cui lo smorzamento α salirebbe a 14,4 m–1, e il coefficiente di amplificazione β addirittura a 278!
In realtà gli studenti più accorti mi faranno notare che non tutte le ipotesi semplificative da noi introdotte sono realistiche. Per esempio, considerare costante il coefficiente h è poco verosimile, dato che la temperatura della sbarra varia enormemente da 300° a 20°C; considerare tuttavia h dipendente dalla temperatura renderebbe impossibile risolvere in maniera semplice la nostra equazione differenziale, richiedendo piuttosto l'uso di calcoli numerici che esulano dalle competenze richieste per comprendere il nostro testo di Termodinamica.
E con questo, almeno per quanto riguarda il presente ipertesto, siamo arrivati davvero ai titoli di coda...

![]()