DATI E LORO ELABORAZIONE:

Inseriamo in una tabella tutti i dati che abbiamo raccolto, nell’ordine: il numero della misurazione, la profondità a cui si trovava la membrana, il livello dell’acqua nel tubo di sinistra, il livello nel tubo di destra e la differenza di pressione in millimetri d’acqua (notare come l’errore si sia sommato).

#

P [cm]

Sx [mm]

Dx [mm]

DP [mm H2O]

1

0 ± 0,1

0 ± 1

0 ± 1

0 ± 2

2

1 ± 0,1

5 ± 1

-5 ± 1

10 ± 2

3

2 ± 0,1

10 ± 1

-10 ± 1

20 ± 2

4

3 ± 0,1

15 ± 1

-15 ± 1

30 ± 2

5

4 ± 0,1

20 ± 1

-20 ± 1

40 ± 2

6

5 ± 0,1

25 ± 1

-25 ± 1

50 ± 2

7

6 ± 0,1

30± 1

-30 ± 1

60 ± 2

8

7 ± 0,1

35 ± 1

-35 ± 1

70 ± 2

9

8 ± 0,1

40± 1

-40 ± 1

80 ± 2

10

9 ± 0,1

45 ± 1

-45 ± 1

90 ± 2

11

10 ± 0,1

50 ± 1

-50 ± 1

100 ± 2

N.B. = per non complicare eccessivamente i calcoli, dal momento che già inizialmente si presentava un dislivello di 5 mL ineliminabile anche dopo numerosi tentativi, abbiamo sottratto 5 ad ogni valore della colonna di sinistra.

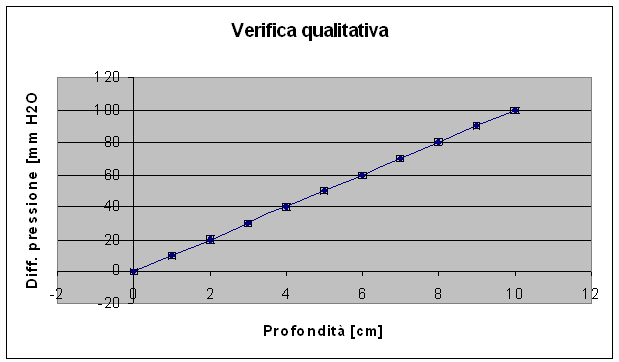
Prima di effettuare qualsiasi altro calcolo, procediamo con una verifica di tipo qualitativo (o euristico), prendendo in considerazione i valori di profondità e variazione di pressione in millimetri d’acqua e collocandoli nel piano cartesiano.

Poi, dal momento che 1 mm H2O = 9,8 Pa, abbiamo calcolato la pressione in Pascal, moltiplicando i risultati della quinta colonna per 9,8.

Per ogni valore dell’ultima colonna si sottintenda quindi un errore pari a ± 2 x 9,8 Pa.

#

P [cm]

Sx [mm]

Dx [mm]

DP [mm H2O]

DP [Pa]

1

0 ± 0,1

0 ± 1

0 ± 1

0 ± 2

0

2

1 ± 0,1

5 ± 1

-5 ± 1

10 ± 2

98

3

2 ± 0,1

10 ± 1

-10 ± 1

20 ± 2

196

4

3 ± 0,1

15 ± 1

-15 ± 1

30 ± 2

294

5

4 ± 0,1

20 ± 1

-20 ± 1

40 ± 2

392

6

5 ± 0,1

25 ± 1

-25 ± 1

50 ± 2

490

7

6 ± 0,1

30± 1

-30 ± 1

60 ± 2

588

8

7 ± 0,1

35 ± 1

-35 ± 1

70 ± 2

686

9

8 ± 0,1

40± 1

-40 ± 1

80 ± 2

784

10

9 ± 0,1

45 ± 1

-45 ± 1

90 ± 2

882

11

10 ± 0,1

50 ± 1

-50 ± 1

100 ± 2

980

 

Calcoliamo ora la pressione ad ogni livello di profondità ricorrendo alla legge di Stevin.

In questo caso, però, la profondità deve essere considerata in metri, mentre P0 si annulla a causa della pressione dell’aria esercitata contemporaneamente sul tubo del manometro a U e sull’acqua nel becher.

  1. P = rgh = 1000 x 9,8 x 0 = 0 Pa
  2. P = rgh = 1000 x 9,8 x 0,01 = 98 Pa
  3. P = rgh = 1000 x 9,8 x 0,02 = 196 Pa
  4. P = rgh = 1000 x 9,8 x 0,03 = 294 Pa
  5. P = rgh = 1000 x 9,8 x 0,04 = 392 Pa
  6. P = rgh = 1000 x 9,8 x 0,05 = 490 Pa
  7. P = rgh = 1000 x 9,8 x 0,06 = 588 Pa
  8. P = rgh = 1000 x 9,8 x 0,07 = 686 Pa
  9. P = rgh = 1000 x 9,8 x 0,08 = 768 Pa
  10. P = rgh = 1000 x 9,8 x 0,09 = 882 Pa
  11. P = rgh = 1000 x 9,8 x 0,1 = 980 Pa

Confrontiamo ora i valori ricavati attraverso questi ultimi calcoli con quelli dell’ultima colonna della tabella per vedere se effettivamente equivalgano.

HOME