Bonaventura Cavalieri

Biografia:
Cavalieri, Bonaventura (Milano 1589 ca. - Bologna 1647), matematico italiano. Gesuita, di formazione umanistica,
si dedicò alla predicazione, ma compì anche studi matematici a Pisa, dove fu allievo di Galileo Galilei.
Nel 1616 si trasferì a Pisa dove divenne allievo di Benedetto Castelli (1577/8-1643), che lo presentò a Galileo.
Dal 1626 si trasferì a Roma, per sostituire il Castelli allo Studio, durante le frequenti assenze. Il giovane aspirava
ad una lettura di matematica, ma per quella di Pisa gli fu preferito Niccolò Aggiunti (1600-1635). Nel 1628, resasi
vacante quella di Bologna per la morte di Giovanni Antonio Magini (1555-1617), Cavalieri chiese aiuto a Galileo che
riuscì a fargliela ottenere.
Nel 1629 ottenne a Bologna la cattedra di matematica che conservò fino alla morte. La sua fama è legata soprattutto
al 'metodo degli indivisibili' rigorosamente sviluppato nell'opera Geometria indivisibilibus continuorum nova quadam
ratione promota (1635). Tale metodo considera qualsiasi grandezza geometrica – linee, piani, solidi – come l'insieme
di costituenti elementari quali punti, linee e piani che vengono denominati 'infiniti indivisibili'. Questa teoria,
che sollevò aspre polemiche tra i contemporanei, influì notevolmente sullo sviluppo della geometria e costituì
un'anticipazione dei principi che avrebbero ispirato il calcolo infinitesimale. Cavalieri compì anche importanti
ricerche nei campi della trigonometria piana e sferica, del calcolo logaritmico, dell'ottica e dell'astronomia,
spetta infatti a lui il merito di aver diffuso l’uso dei logaritmi in Italia.
I suoi studi:
Bonaventura Cavalieri (1598-1647), allievo di Galileo e professore in un liceo di Bologna, fu influenzato da
Keplero e da Galileo e spinto da quest’ultimo a occuparsi dei problemi del calcolo infinitesimale.
Cavalieri sviluppò le idee di Galileo e di altri sugli indivisibili, incorporandole in un metodo geometrico e
pubblicò un’opera sull’argomento intitolata “Geometria indivisibilibus continuorum nova quadam ratione promota”
(1635). Egli considera un’area come costituita da un numero indefinito di segmenti paralleli
equidistanti e un volume come composto da un numero indefinito di aree piane parallele; questi elementi sono
detti rispettivamente indivisibili di area e di volume.
Cavalieri si rende conto che il numero di indivisibili
che costituiscono un’area o un volume deve essere indefinitamente grande, ma non cerca di approfondire questo
fatto.
In parole semplici, gli indivisibilisti sostenevano, come dice Cavalieri nelle sue
“Exercitationes geometricae sex”
(1647), che una retta è composta da punti come un rosario da grani; che un piano è composto
da rette come una stoffa da fili e che un volume è composto
da aree piane come un libro da pagine. Essi ammettevano tuttavia che gli elementi costituenti fossero in numero
infinito.
Il metodo o principio di Cavalieri è illustrato dalla seguente
proposizione, che può naturalmente essere
dimostrata in altri modi:
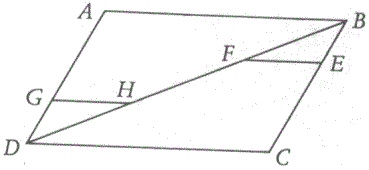
Per provare che il parallelogramma ABCD ha area doppia di quelle dei triangoli ABD
o BCD, Cavalieri osservava che, se GD = BE, allora GH = FE. I triangoli ABD e BCD sono perciò composti da un
numero uguale di segmenti uguali come GH ed EF e devono perciò avere aree uguali.
In modo analogo trattava l’area compresa fra due curve; considerando le aree principio Cavalieri dimostrò che il volume di un cono è uguale a 1/3 di quello del cilindro come somma delle ordinate, e se le ordinate stanno l’un l’altra in un rapporto costante, allora, dice Cavalieri, anche le aree stanno nello stesso rapporto.
Cavalieri aveva successo nell’ottenere risultati corretti perché applicava il suo principio al calcolo di rapporti di aree e di volumi in cui il rapporto degli indivisibili che li costituiscono era costante. Gli indivisibili di Cavalieri furono criticati dai suoi contemporanei e Cavalieri tentò di rispondere alle critiche, senza però essere in possesso di una giustificazione rigorosa. Nonostante le critiche, il metodo degli indivisibili venne applicato intensivamente da molti matematici. Altri, come Fermat, Pascal e Roberval, si servirono del metodo e anche dello stesso suo linguaggio adoperando espressioni come la somma delle ordinate, ma pensavano all’area come a una somma di rettangoli infinitamente piccoli piuttosto che come a una somma di segmenti.
Nell'opera "Geometria indivisibilibus continuorum nova quadam ratione promota" (Bologna, 1635), dedicata a Giovanni Ciampoli (1589-1643), anticipò il calcolo infinitesimale leibnitiano e ebbe la trovata di genio di applicare gli indivisibili alla spirale di Archimede. Dato l'alto grado di tecnicismo, il libro, assai apprezzato nella cerchia galileiana e giudicato dai postumi un capolavoro, non fu compreso fino in fondo dai contemporanei. Lo stesso Galileo, travolto in quegli anni dalla condanna, non poté concentrare molte attenzioni sull'opera del matematico milanese.
Durante la sua vita entrò in polemica col gesuita Paul Guldin (1577-1643), che lo aveva accusato di aver plagiato Keplero e di aver contraddetto in certi particolari Galileo senza appigli sufficienti, gli rispose con la Trigonometria plana e sphaerica linearis et logaritmica (Bologna, 1643) e con la terza delle Exercitationes geometricae sex (Bologna, 1647), riuscendo anche a dimostrare con gli indivisibili un teorema pensato, ma non completamente dimostrato, dallo stesso Guldin, ormai morto.