Testo
Il candidato risolva uno dei due problemi e 5 dei 10 quesiti del questionario.
PROBLEMA 1
Sia f la funzione definita da: ![]()
1. Disegnate il grafico
G di f.
2. Nel primo quadrante degli assi cartesiani,
considerate la retta y = c che interseca G in due punti distinti e le
regioni finite di piano R e S che essa delimita con
G. Precisamente: R delimitata dall'asse y, da
G e dalla retta y = c.
3. Determinate c in modo che
R e S siano equivalenti e determinate le corrispondenti ascisse
dei punti di intersezione di G con la retta y = c;
4.
determinate la funzione g il cui grafico è simmetrico di G
rispetto alla retta ![]()
PROBLEMA 2
ABC è un triangolo rettangolo di ipotenusa BC.
1. Dimostrate che la mediana relativa a BC è congruente alla metà di
BC.
2. Esprimete le misure dei cateti di ABC in funzione delle
misure, supposte assegnate, dell'ipotenusa e dell'altezza ad essa relativa.
3. Con BC=![]() metri, determinate il cono K di volume massimo
che si può ottenere dalla rotazione completa del triangolo attorno ad uno dei
suoi cateti e la capacità in litri di K.
metri, determinate il cono K di volume massimo
che si può ottenere dalla rotazione completa del triangolo attorno ad uno dei
suoi cateti e la capacità in litri di K.
4. Determinate la misura
approssimata, in radianti ed in gradi sessagesimali, dell'angolo del settore
circolare che risulta dallo sviluppo piano della superficie laterale del cono
K.
QUESTIONARIO
1. Trovate due numeri reali a e b, a![]() b, che hanno
somma e prodotto uguali.
b, che hanno
somma e prodotto uguali.
2. Provate che la superficie totale di un cilindro
equilatero sta alla superficie della sfera ad esso circoscritta come 3 sta a 4.
3. Date un esempio di funzione f(x) con un massimo relativo in (1,
3) e un minimo relativo in (-1, 2).
4. Dimostrate che l'equazione
![]() ammette una
e una sola soluzione reale.
ammette una
e una sola soluzione reale.
5. Di una funzione g(x) , non costante,
si sa che: ![]()
Trovate una espressione di g(x).
6.
Verificate che le due funzioni ![]() hanno la stessa
derivata. Quale giustificazione ne date?
hanno la stessa
derivata. Quale giustificazione ne date?
7. Un triangolo ha due lati e
l'angolo da essi compreso che misurano rispettivamente a, b e
d. Quale è il valore di d che massimizza l'area del triangolo?
8. La
misura degli angoli viene fatta adottando una opportuna unità di misura. Le più
comuni sono i gradi sessagesimali, i radianti, i gradi centesimali. Quali ne
sono le definizioni?
9. Calcolate: ![]()
10.
Considerate gli insiemi { A={1,2,3,4} e B={a,b,c} ; quante sono le applicazioni
(le funzioni) di A in B?
SOLUZIONE
Problema 1
 1. La
funzione f(x) è definita in
1. La
funzione f(x) è definita in ![]() , passa per
l’origine degli assi ed è simmetrica rispetto a tale punto.
, passa per
l’origine degli assi ed è simmetrica rispetto a tale punto.
Taglia l’asse
delle ascisse nei punti ![]() e
e ![]() .
.
Si ha f ‘ (x) = ![]() per
per ![]() e
e ![]() .
.
La funzione
ha dunque un minimo relativo ![]() ed un massimo
relativo
ed un massimo
relativo ![]()
 2. e 3.
Indicati con C e D i punti in cui la retta
2. e 3.
Indicati con C e D i punti in cui la retta
y = c interseca G, con A e
B le rispettive proiezioni sull’asse x e con b l’ascissa
del punto B.
L’equivalenza delle superfici R ed S implica
che l’area del rettangolo OBCE è uguale all’area della regione limitata dalla
curva G, dall’asse x e dalla retta BC, cioè si ha:
Area (OBCE) =
![]() =
AreaReg
=
AreaReg  .
.
Cioè: ![]()
![]()
![]()
Ma il punto
C (b;c) appartiene al grafico e pertanto si ha il seguente
sistema:
![]()
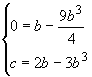
![]()
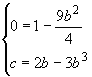
![]()
![]()
Il sistema ovviamente ammette anche altre soluzioni, ma non
soddisfano le limitazioni poste (primo quadrante).
La retta richiesta ha
pertanto equazione ![]()
4. La simmetria rispetto alla retta ![]() ha equazioni:
ha equazioni:
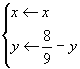
La
funzione g richiesta ha pertanto equazione: ![]()
ovvero ![]()
Problema 2
 1. La
mediana coincide con il raggio del cerchio circoscritto al triangolo il cui
diametro è l’ipotenusa.
1. La
mediana coincide con il raggio del cerchio circoscritto al triangolo il cui
diametro è l’ipotenusa.
2. Posto AB = x , AC = y, BC = a, AH = h,
si
ha il sistema simmetrico: 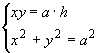
le cui soluzioni, convenendo ![]() , sono:
, sono:
3. Posto ![]() e l’angolo
e l’angolo ![]() , per ragioni di simmetria, è sufficiente considerare il caso
, per ragioni di simmetria, è sufficiente considerare il caso
![]() . Si
distinguono due casi: rotazione intorno al cateto
. Si
distinguono due casi: rotazione intorno al cateto ![]() , rotazione
intorno al cateto
, rotazione
intorno al cateto ![]() . I volumi di K, nei rispettivi due casi,
sono:
. I volumi di K, nei rispettivi due casi,
sono:![]()
![]() .
.
Nell’intervallo considerato è sempre ![]() e quindi
e quindi ![]() . Il massimo va
pertanto calcolato sulla funzione
. Il massimo va
pertanto calcolato sulla funzione ![]()
Derivando si
ha: y ‘ = ![]() . Dallo studio del segno della derivata si ottiene il massimo
quando
. Dallo studio del segno della derivata si ottiene il massimo
quando ![]() ,
,
che dà l’angolo ![]() .
.
Il volume
massimo richiesto è![]()
![]() litri
litri![]() litri.
litri.
4. La misura di ![]() in radianti
è:
in radianti
è: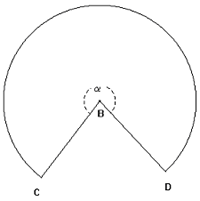
![]() rad
rad![]()
![]() 5.13 rad.
5.13 rad.
La sua misura in gradi sessagesimali è
![]() ° =
° =
![]()
![]() 294°
294°
3. 

Autori
Prof. Gianfranco Pistoni - Liceo Scientifico “ARCHIMEDE” Roma
Prof. Ferruccio Rohr - Liceo Scientifico “NOMENTANO” Roma