![]()
|
I fuochi d'artificio erano di Gandalf, ed ora li proiettava nel cielo creando effetti particolari di piogge incandescenti e di razzi multicolori... SdA, libro I, capitolo I |
Questa volta la prenderemo molto alla lontana, almeno apparentemente. Come si sa, il primissimo capitolo del Signore degli Anelli è intitolato "Una festa a lungo attesa", perché descrive il party di addio di Bilbo Baggins, che ha ormai raggiunto l'età di 111 anni e ha allestito una memorabile festa di compleanno a cui sono invitati tutti gli abitanti di Hobbiville; alla fine di essa egli sparirà nel nulla, essendosi infilato l'Anello, per trasferirsi segretamente a Gran Burrone, ospite di Elrond. In particolare il party viene accompagnato da splendidi fuochi d'artificio realizzati da Gandalf, conoscitore di tutti i segreti del fuoco. Ecco il passo in questione
«
Si vedeva solo una quantità di gente che mangiava e beveva senza interruzione,
e ciò dalle undici alle sei e mezzo, ora in cui cominciò lo spettacolo
pirotecnico.
I fuochi d'artificio erano di Gandalf: non solo era stato lui a portarli fino a
casa Baggins, ma li aveva anche progettati e costruiti, ed ora li proiettava nel
cielo creando effetti particolari di piogge incandescenti e di razzi
multicolori. Nel frattempo veniva
distribuito un gran numero di petardi, girandole, mortaretti, castagnole,
fiaccole, candele nane, fontane elfiche e scatole a sorpresa. Erano gli uni più
belli degli altri. L'arte e l'abilità di Gandalf si erano perfezionate con il
passar del tempo. Il cielo era illuminato a giorno: voli di scintillanti uccelli
dal dolce canto; verdi alberi dai tronchi di fumo
scuro, le cui foglie si aprivano come tutta una primavera sbocciata in un solo
attimo; rami incandescenti dai quali piovevano sfavillanti
fiori sui piccoli Hobbit
strabiliati, boccioli che si dileguavano in un profumo soave prima di sfiorare i
loro visi rivolti verso l'alto; zampilli di farfalle svolazzanti che brillavano
tra gli alberi; colonne di fuoco colorato
si innalzavano trasformandosi in aquile, nani e falangi di candidi
cigni in volo; tempeste rosse,
acquazzoni dalle gocce color limone; una foresta di lance
argentate
che si rizzò nello spazio col rumore di un esercito all'assalto, per piombare
poi nell'acqua fischiando come cento serpenti arroventati. Vi fu poi l'ultima
sorpresa in onore di Bilbo che, come aveva previsto Gandalf, sbigottì ed
emozionò i presenti. Le luci si spensero; una massa di fumo s'innalzò: prese
la forma di una montagna dalla cima incandescente vista in lontananza. Vomitava fiamme
verdi e scarlatte,
quindi dal suo ventre volò fuori un drago d'oro rosso,
non in grandezza naturale, ma estremamente verosimile; sputava fuoco dalle
possenti mascelle e lanciava verso il pubblico sguardi infuocati e terribili; ci
fu un ruggito; poi il drago passò sibilando tre volte sulla testa della gente.
Tutti si gettarono a terra e molti batterono la testa. Il drago tornò a passare
su di loro alla velocità di un treno, fece un salto mortale e scoppiò nel cielo di Lungacque
con un boato assordante.
»
(SdA, libro
I, cap. I)
Come si vede, nella fantasmagorica descrizione dei fuochi artificiali domina un tripudio di colori, che abbiamo evidenziato rispetto al resto del testo: razzi multicolori, alberi verdi, fiori sfavillanti, fuoco colorato, candidi cigni, tempeste rosse, un acquazzone di pioggia gialla, lance argentate, fiamme verdi e scarlatte, un drago d'oro rosso. La descrizione è tanto vivida, da far sorgere agli appassionati di Tolkien più di un interrogativo, rintracciabile nei forum, come questo: se nella Terra di Mezzo i depositari del sapere più antico conoscono la tecnologia dei fuochi d'artificio (di probabile origine númenoreana, vista l'avanzata civiltà dell'Isola dei Re), perchè non possiedono invece armi da fuoco, dato che nel "nostro" mondo proprio dai fuochi artificiali venne derivata la polvere da sparo? In effetti solo Saruman, in tutto l'universo di Tolkien, fa uso di una mina per aprire una breccia nelle fortificazioni nemiche durante l'Assedio del Fosso di Helm; Sauron, colui che più potrebbe trarre beneficio da una simile tecnologia in battaglia, sembra ignorarne l'esistenza, anche se sia Curunír (Saruman) che Olórin (Gandalf) che Sauron sono tutti e tre dei Maiar, e Morgoth è detto essere dotato di tutti i doni degli Ainur. Il problema resta aperto, nonostante tutte le ingegnose soluzioni escogitate dai fan per dargli una soluzione, e molti appassionati si sono chiesti come avrebbe dovuto essere riscritto il Legendarium, se Uomini, Elfi, Nani e Orchi avessero imbracciato moschetti, pistole, obici e mortai. Ovviamente non è certo di questo dilemma che vogliamo discutere in questa sede, quanto piuttosto concentrarci sull'origine di quei meravigliosi colori che Tolkien ha saputo descrivere con tanta maestria.

Gandalf (a sinistra) e Niels Bohr (a destra) sullo sfondo di uno spettacolo pirotecnico
Noi sappiamo che i materiali utilizzati per realizzare i fuochi d'artificio sono miscele che bruciano rapidamente, e che contengono l'ossigeno necessario alla combustione; il materiale più adoperato è la polvere nera, una miscela di nitrato di potassio, carbone e zolfo in proporzioni variabili, per ottenere diversi valori della velocità di combustione. I colori vengono dati dalla combustione, insieme alla polvere, di varie sostanze. Alluminio e magnesio ad esempio producono luce bianca; antimonio, arsenico e zinco producono luce bianco-azzurra; i composti del sodio danno luce gialla; quelli del calcio e dello stronzio danno luce rossa; quelli del bario e del rame, luce verde. Ma perchè? Intendo dire: perchè ciascun elemento produce luce proprio di quel colore, e non un'altra? Per rispondere a questa domanda, la chimica da sola non ci basta, e neppure la Fisica Classica (quella fondata da Galilei e Newton): dobbiamo inoltrarci fin nell'interno dell'atomo, avventura che inaspettatamente ci permetterà di introdurre alcuni dei concetti fondamentali della Fisica Atomica e della Meccanica Quantistica: un risultato davvero incredibile, se si pensa che siamo partiti da un semplice spettacolo pirotecnico!

Tanto per cominciare, il concetto di atomo è molto più antico di quanto si pensi. Secondo Aristotele, il primo ad introdurre tale concetto fu il filosofo greco Leucippo di Mileto, vissuto nel V secolo a.C., del quale però nulla sappiamo al di là di quanto Aristotele ci racconta di lui. A sistematizzare la teoria atomica nei suoi dettagli fu invece Democrito di Abdera (460-370 a.C.), il quale sostenne che la materia non è infinitamente divisibile (come propugnava invece Aristotele), ma è costituita da mattoni fondamentali detti atomi (in greco "non più divisibili"), i quali si aggregherebbero e disgregherebbero a caso, determinando la formazione dei corpi che costituiscono l'universo. Tale teoria fu poi ripresa da Epicuro (342-270 a.C.) e dal poeta latino Tito Lucrezio Caro (94-50 a.C.), che descrisse la teoria atomica nel suo capolavoro in versi "De Rerum Natura". Osteggiato dal Cristianesimo perchè il concetto di aggregazione e disgregazione casuale degli atomi faceva a pugni con il concetto di Provvidenza (Dante pone nel Limbo « Democrito che 'l mondo a caso pone », Inf. IV, 136), l'atomismo fu riabilitato già nel seicento dall'abate Pierre Gassendi (1592-1655), che nel suo "Syntagma philosophiae Epicuri" del 1649 interpretò la filosofia epicurea in senso cristiano, usandola per respingere l'astratta metafisica cartesiana. Nell'ambito della nuova visione scientifica dell'universo inaugurata da Galileo Galilei, Gassendi fu il primo a riconoscere che l'atomismo fosse l'unica teoria fisica compatibile con il metodo di indagine scientifica che si andava delineando sempre più chiaramente, in contrapposizione alle teorie aristoteliche ormai imperanti; non a caso, Ludovico Geymonat affermò a ragione che l'atomismo di Democrito ebbe un ruolo determinante, nel XVI e XVII secolo, per la nascita stessa della scienza moderna. Il trionfo dell'atomismo coincise con la grande stagione del Razionalismo e poi dell'Illuminismo: il primo ad introdurre l'atomo non già come concetto filosofico ma come unica realtà scientifica sulla quale era possibile fondare l'intera chimica fu l'inglese John Dalton (1766-1844), che nel 1803 formulò cinque ipotesi fondamentali:
a) la materia è formata da atomi piccolissimi, indivisibili e
indistruttibili;
b) tutti gli atomi di uno stesso elemento sono identici e hanno uguale massa;
c) gli atomi di un elemento non possono essere convertiti in atomi di altri
elementi;
d) gli atomi di un elemento si combinano, per formare un composto, solamente con numeri interi di atomi di altri
elementi;
e) gli atomi non possono essere né creati né distrutti, ma si trasferiscono interi da un composto ad un altro.
Dalton dedusse queste ipotesi dalla cosiddetta Legge delle Proporzioni Multiple, da lui stesso enunciata: quando un elemento si combina con la stessa massa di un altro per formare composti diversi, le masse del primo elemento stanno tra loro in rapporti esprimibili mediante numeri interi e piccoli. La quarta ipotesi deriva invece dalla Legge delle Proporzioni Definite, enunciata nel 1799 dal francese Joseph Proust (1754-1826): quando due o più elementi reagiscono per formare un determinato composto, si combinano sempre secondo proporzioni in massa ben definite e costanti. Come si vede, il concetto di atomo era entrato stabilmente a far parte della Chimica moderna. Per tutto l'ottocento, si guardò all'atomo nella sua accezione etimologica, cioè come il frammento più piccolo ed indivisibile di materia cui si potesse pensare. Le cose cambiarono in seguito alla scoperta dell'elettrone.
Le prime idee circa una possibile struttura discontinua dell'elettricità emersero nel 1835 in seguito agli esperimenti di Michael Faraday (1791-1867) sulle celle elettrolitiche: dallo studio della conduzione nelle soluzioni emerse infatti che, come la materia e fatta di atomi, anche quello che allora era chiamato "fluido elettrico" doveva essere formato da corpuscoli estremamente piccoli, ma questo fatto divenne una certezza in seguito alla scoperta nel 1869 dei raggi catodici. Dopo l'invenzione delle pompe in grado di creare il vuoto spinto dentro appositi tubi di vetro, i tedeschi Julius Plücker (1801-1868) e Johann Wilhelm Hittorf (1824-1914) osservarono come, inserendo alle due estremità di un tubo a vuoto (detto appunto tubo di Plücker) due elettrodi collegati rispettivamente all'anodo e al catodo di un generatore di alta tensione, il tubo emanava una tenue luminosità, la cui intensità dipendeva dalla differenza di potenziale agli elettrodi e dalla pressione residua nel tubo. Successivamente il britannico Sir William Crookes (1832-1919) fece notare che, riducendo ulteriormente la pressione nel tubo di Plücker, l'anodo veniva illuminato da una luce molto intensa, prodotta da radiazioni uscenti dal catodo. Eugene Goldstein (1850-1930) chiamò tali radiazioni raggi catodici, ma ne ignorava la natura. Nel 1895 il francese Jean Baptiste Perrin (1870-1942) mise in evidenza come tali raggi avessero in realtà natura corpuscolare, perchè erano in grado di mettere in rotazione un mulinello, e quindi erano dotati di massa; nel 1897 il britannico Joseph John Thomson (1856-1940) arrivò a calcolare il rapporto fra la carica e la massa di quei corpuscoli, e li battezzò elettroni. Era stata scoperta la prima particella subatomica (per questo Thomson ricevette il Premio Nobel per la Fisica nel 1806). Allo stesso Thomson si deve il primo modello di atomo che evidenziava una sua struttura interna: secondo lui l'atomo era una sfera di carica positiva, nel quale gli elettroni erano contenuti come le uvette in un plumcake, tipico dolce anglosassone, da cui il nome di "modello a plumcake" dell'atomo. Era un modello semplicistico, ma permetteva di spiegare perchè le sostanze, riscaldate, emettono luce: dentro la sfera carica gli elettroni possono muoversi solo di moto armonico, e così facendo generano un'onda sinusoidale, che rappresenta l'onda luminosa osservata. Attraverso complessi calcoli, Thomson e i suoi collaboratori tentarono di determinare le lunghezze d'onda osservate sperimentalmente degli spettri degli elementi, ma con risultati poco soddisfacenti.
Un passo avanti notevole venne compiuto dal fisico neozelandese Ernest Rutherford (1871-1937), allievo di Thomson, studiando lo scattering, cioè la diffusione, delle particelle alfa generate da un isotopo radioattivo contro una sottilissima lamina d'oro, come si vede nel disegno sottostante. Se l'atomo fosse una semplice palla di carica positiva, le particelle alfa che lo investono dovrebbero subire deflessioni nulle o assai ridotte, come accade sparando proiettili dentro un covone di fieno. Invece Rutherford osservò angoli di deflessione anche notevoli, ed alcune particelle alfa addirittura tornavano indietro. Se noi spariamo contro un covone e notiamo che esso respinge i proiettili secondo angoli notevoli, siamo costretti a concludere che dentro il covone c'è un grosso sasso, o un ferro da stiro, contro cui i proiettili rimbalzano. Allo stesso modo, Rutherford concluse che quasi tutta la carica positiva dell'atomo deve essere concentrata in un nucleo centrale, di dimensioni assai ridotte, mentre gli elettroni gli ruotano attorno come i pianeti intorno al sole. Era il 1911 ed era nato il modello planetario, tuttora utilizzato per spiegare grosso modo come sono distribuite le cariche dentro l'atomo.
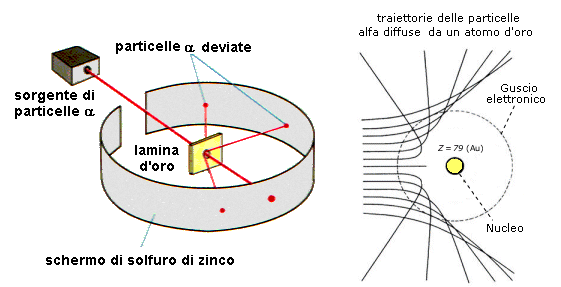
Purtroppo però l'atomo descritto da Rutherford è fatalmente instabile. Infatti gli elettroni sono particelle cariche, e come tali obbediscono alle famose quattro equazioni di Maxwell. Ma l'elettrodinamica basata su tale leggi ci insegna che una carica, se accelerata, irraggia tutta la propria energia nello spazio circostante, sotto forma di radiazione elettromagnetica (è il principio in base al quale funzionano le antenne). Ipotizzando che l'elettrone si muova di moto circolare uniforme intorno al nucleo, esso sarebbe soggetto inevitabilmente ad un'accelerazione centripeta, e di conseguenza irraggerebbe tutta la sua energia cinetica nello spazio, finendo per ricadere a spirale sopra il nucleo in un tempo brevissimo, appena 10–8 secondi.
Dunque tutto il modello planetario dell'atomo è da buttare al macero? Certamente no, vista anche la sua estrema semplicità ed eleganza; il famoso rasoio di Occam infatti ci insegna che la soluzione più semplice in genere è quella corretta. Si tratta solo di modificare questo modello, per giustificare perchè l'elettrone può continuare a ruotare attorno al nucleo senza perdere energia, restando quindi su un'orbita stazionaria. La soluzione giusta la trovò Niels Bohr (1895-1962), brillante fisico danese, rampollo di una famiglia della buona borghesia di Copenaghen (suo padre, Christian Bohr, insegnava Fisiologia all'Università di quella città, e suo fratello Harald, matematico, partecipò alle Olimpiadi del 1908 giocando nella Nazionale Danese di calcio e vincendo la medaglia d'argento). Allievo di Rutherford all'Università di Manchester, fu definito dal suo maestro « uno dei giovani più intelligenti che io abbia mai incontrato ». Evidentemente Rutherford aveva ragione, perchè Bohr, resosi conto che le leggi della Fisica Classica erano insufficienti a giustificare la validità di un modello peraltro in perfetto accordo con le verifiche sperimentali, decise di rivolgersi ad una nuova Fisica, quella appena introdotta da un geniale professore tedesco, Max Planck (1858-1947).
Quest'ultimo cercava di risolvere il problema del cosiddetto spettro di corpo nero. Si dice corpo nero un oggetto che assorbe qualunque radiazione ricevuta, riemettendo poi energia secondo un ben preciso spettro di lunghezze d'onda. Come conferma l'esperienza, la forma di tale spettro dipende unicamente dalla temperatura assoluta della sorgente, non dal materiale di cui essa è costituita. La radiazione del corpo nero presenta tipicamente un massimo per una certa frequenza, crescente all'aumentare della temperatura, mentre diminuisce sia per le alte che per le basse frequenze. Applicando al corpo nero le leggi dell'Elettrodinamica classica, basate sulle equazioni di Maxwell, si giunge però a conclusioni in totale disaccordo con l'esperienza. Ipotizziamo infatti che tutti gli atomi di cui il corpo nero è composto siano oscillatori armonici classici, che obbediscono a quelle equazioni. I fisici inglesi John William Strutt, Terzo Barone di Rayleigh (1842-1919), e Sir James Hopwood Jeans (1877-1946) ricavarono, su questa ipotesi, la cosiddetta Legge di Rayleigh e Jeans, che descriveva in modo corretto lo spettro di corpo nero per basse frequenze, ma falliva completamente per frequenze più elevate. Infatti, in contraddizione con le osservazioni sperimentali, tale legge affermava che l'intensità dovrebbe crescere indefinitamente all'aumentare della frequenza. Se così fosse, ogni oggetto radiante che si comporta come un corpo nero, incluso un normale forno da cucina, dovrebbe diventare una pericolosissima sorgente di raggi ultravioletti e di raggi X. Questo fenomeno prende il nome di "catastrofe ultravioletta", ed evidentemente non ha luogo, né nel nostro universo, né nel mondo secondario di Tolkien: lo spettro di corpo nero ci dice che l'intensità di radiazioni con frequenze nell'ambito dei raggi ultravioletti, X o gamma è praticamente zero.
L'impotenza delle equazioni di Maxwell ad interpretare lo spettro di corpo nero mise in crisi, di fatto, i fondamenti della Fisica Classica, che già negli stessi anni stava ricevendo un duro colpo dall'esperienza di Michelson e Morley (descritta in questa pagina), i quali misero in evidenza l'inesistenza dell'etere luminifero, spianando la strada alla grande rivoluzione di Albert Einstein, cui ho dedicato un altro ipertesto. Orbene, il 14 dicembre 1900 Max Planck, docente di Fisica Teorica all'Humboldt-Universität di Berlino, e tutt'altro che simile, per aspetto e comportamento, ad un rivoluzionario giacobino, presentò all'Accademia Tedesca delle Scienze un lavoro intitolato "Zur theoriedes Gazetzes der Energieverteilung in Normalspektrum" ("Sulla legge della distribuzione dell'energia negli spettri normali"), con il quale riuscì perfettamente ad interpretare la radiazione spettrale di corpo nero, facendo però ricorso ad un'ipotesi rivoluzionaria: l'energia della radiazione emessa dal corpo nero non può assumere valori qualsiasi, ma solo multipli di un valore fondamentale, detto quanto di energia, pari ad E = h f, dove f è la frequenza della radiazione, ed h è una costante che oggi è universalmente nota come costante di Planck, ed è uno dei parametri basilari della Fisica:
h = 6,626 x 10–34 J s
Come un fantasma onnipresente, questa costante salta fuori ogni qualvolta si studia un fenomeno legato all'infinitamente piccolo. La sua estrema piccolezza invece esclude un suo ruolo nelle leggi che descrivono fenomeni macroscopici, dove continua a valere la Fisica di Galilei, Newton e Maxwell; per questo, i quanti di Planck sono inosservabili su scala umana, mentre assumono un'importanza basilare nella Fisica Atomica e nella Fisica Nucleare. Dal termine "quanto" scaturisce ovviamente il nome di Fisica Quantistica dato ad ogni studio che coinvolge la diabolica h. A dir la verità, una volta introdotto il concetto di quanto, il mite professore berlinese ne fu quasi spaventato, rendendosi conto che esso assestava una spallata micidiale a tutto il perfettissimo edificio della Fisica Classica, considerato una struttura concettuale completa, sicura e definitiva, e tentò di modificare la sua teoria per farla rientrare nel tranquillo alveo dell'elettrodinamica maxwelliana, ma non ci fu nulla da fare. Naturalmente, se persino lo stesso Planck era scettico circa la quantizzazione dell'energia, era logico che la stragrande maggioranza dei suoi contemporanei guardasse a questa ipotesi come a qualcosa di stravagante, se non addirittura di sacrilego, da eliminare al più presto dal panorama della Fisica. Questo atteggiamento però non fu condiviso da un certo Albert Einstein, che nel 1905 usò proprio la nuovissima legge E = h f per interpretare un altro fenomeno fino ad allora sfuggito ad ogni tentativo di interpretazione attraverso l'elettrodinamica classica, l'effetto fotoelettrico. Con il suo lavoro "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt" ("Sull'emissione e la trasformazione della luce da un punto di vista euristico"), per il quale (e non per le successive ricerche sulla Relatività Ristretta e Generale) Einstein riceverà il Premio Nobel per la Fisica nel 1921, il genio tedesco mostrò una volta per tutte che i fondamenti della teoria dei quanti potevano rappresentare la chiave per aprire molte porte del mondo atomico e subatomico, rimaste fino ad allora ermeticamente chiuse.

Chi ne approfittò per "correggere" il modello planetario di Rutherford, fu proprio Niels Bohr. Per spiegare come, però, dovremo riprendere in mano proprio l'argomento con il quale abbiamo aperto questa lezione, cioè il colore dei fuochi pirotecnici con i quali Gandalf ha festeggiato il compleanno di Bilbo. Infatti tali colori possono essere previsti e studiati facendo uso della spettroscopia. Porta questo nome la scienza che si occupa dell'analisi degli spettri luminosi emessi dalle varie sostanze quando vengono eccitate, in genere riscaldandole ad alta temperatura. In particolare essa studia, in funzione della lunghezza d'onda, la distribuzione energetica delle onde elettromagnetiche emesse o assorbite dai costituenti della materia. Tale disciplina nacque quando Isaac Newton (1642-1727) mise in evidenza la decomposizione della luce bianca nelle sue componenti monocromatiche per mezzo di un prisma trasparente, il cosiddetto fenomeno della dispersione cromatica; il termine "spettro" è stato ideato proprio da Newton. Nella Terra di Mezzo tale fenomeno è ben noto, perchè viene citato da Saruman durante il drammatico dialogo con Gandalf che portò all'incarcerazione di questi sulla cima del pinnacolo di Orthanc, come lo stesso Stregone narra ai suoi amici durante il Consiglio di Elrond:
«
Lo guardai, e vidi che le sue vesti non erano bianche come mi era parso, bensì
tessute di tutti i colori, che quando si muoveva scintillavano e cambiavano
tinta, abbagliando quasi la vista. "Preferivo il bianco", dissi.
"Bianco!" sogghignò. "Serve come base. Il tessuto bianco può
essere tinto, la pagina bianca ricoperta di scrittura, e la
luce bianca decomposta." »
(SdA, libro II, cap.
II)
Comunque, a partire dal 1830 la spettroscopia assurse al rango di scienza esatta, grazie ai tedeschi Robert Bunsen (1811-1899) e Gustav Robert Kirchhoff (1824 -1887), lavorando insieme all'Università di Heidelberg, costruirono il primo spettroscopio moderno, e si resero conto che gli spettri ottenuti dalla luce emessa dai vari elementi cambiavano da sostanza a sostanza, e nessun composto aveva uno spettro identico a quello di un altro; in pratica, dalla distribuzione delle cosiddette "righe spettrali" (o "righe di Fraunhofer"), scoperte nel 1814 da Joseph von Fraunhofer (1787-1826) nello spettro della luce solare, era possibile risalire alla composizione chimica di qualsiasi oggetto. Per questo l'analisi spettroscopica divenne in breve uno dei più validi sistemi di indagine per identificare e studiare le proprietà della materia. È vero che uno stesso elemento può emettere spettri distinti (alcune righe appaiono, altre scompaiono), ma ciò deriva dal grado e dalla modalità di eccitazione; ogni spettro di righe è sempre caratteristico dell'elemento in quelle determinate condizioni di eccitazione. Naturalmente noi studieremo insieme lo spettro a righe dell'atomo di idrogeno, cioè l'atomo più semplice di tutti; non a caso, tale spettro è stato il primo a venire interpretato, e poi è servito da modello per descrivere e suddividere in serie le ben più complesse distribuzioni di righe negli spettri degli altri elementi.
Modello didattico di spettroscopio (cliccate per ingrandire)
Mediante l'analisi spettroscopica, Bunsen e Kirchhoff scoprirono due elementi fin qui sconosciuti, il rubidio e il cesio, e misero le basi della moderna astrofisica, deducendo dagli spettri delle stelle la loro composizione chimica (la prima stella diversa dal Sole del quale venne studiato lo spettro fu Vega, nel 1872). Inoltre fu proprio usando tecniche spettroscopiche che l'inglese Sir Joseph Norman Lockyer (1836-1920) e il francese Pierre Jules César Janssen (1824-1907), indipendentemente l'uno dall'altro nello stesso anno 1868, scoprirono nelle righe spettrali del Sole delle righe fino ad allora sconosciute, non appartenenti a nessun elemento tra quelli noti; compresero così di essere davanti ad un nuovo elemento, che fu chiamato elio (in greco "Sole"), ritenendo che esso esistesse solo nell'astro solare; in seguito lo scozzese Sir William Ramsay (1852-1916) lo identificò anche sulla Terra.
Se si osserva attraverso un prisma la luce emessa da una sostanza opportunamente eccitata (spesso scaldata fino a portarla allo stato aeriforme, si ottiene la formazione di uno spettro di emissione, che può essere di vari tipi:
a) spettro
continuo, formato da una successione continua di frequenze, dal rosso al
violetto nel visibile. Di solito viene e messo dai solidi e dai liquidi
riscaldati.
b) spettro a righe: è formato da una successione
discreta di righe che possono estendersi dall'infrarosso fino all'ultravioletto.
Questo vuol dire che l'elemento riscaldato non emette tutte le lunghezze d'onda
possibili in un dato intervallo, ma solo particolari lunghezze d'onda,
corrispondenti a particolari colori nella regione del visibile.
c) spettro a bande: è formato da una serie di
righe fittissime che si addensano intorno a certe lunghezze d'onda, in modo da
dar vita ad una serie di bande continue. Viene in genere emesso da gas formati
da molecole poliatomiche.
Noi ci occuperemo in particolare dello spettro a righe. Si noti che si può avere anche uno spettro di assorbimento: facendo passare un fascio di luce bianca attraverso una data sostanza, in genere attraverso un gas o dei vapori, nello spettro continuo appaiono delle righe scure trasversali, segno del fatto che la sostanza ha "assorbito" determinate frequenze. Tali sono le righe di Fraunhofer osservate nello spettro solare: la luce dell'astro attraversa i suoi strati più esterni, i cui componenti assorbono parte di tale luce. Oggi sappiamo ad esempio che le righe catalogate da Fraunhofer come A e B (le meglio visibili) sono dovute all'ossigeno, la riga C all'idrogeno (quella che nel seguito chiameremo Hα), le righe D1 e D2 al sodio e la D3 all'elio. Confrontando gli spettri di emissione e di assorbimento di una medesima sostanza, nel 1859 Gustav Kirchhoff si accorse che le righe scure di assorbimento corrispondono perfettamente alle righe chiare di emissione; in altre parole, ogni sostanza è in grado di assorbire quelle lunghezze d'onda che nelle stesse condizioni fisiche è capace di emettere. Questo è oggi noto come il Principio di Inversione dello Spettro.
A questo punto, però, sorge un problema. Le righe spettrali emesse dagli atomi di un dato elemento presentano una successione di righe, e quindi di lunghezze d'onda, che apparentemente appaiono distribuite senza alcuna regolarità. Perchè dunque certi elementi emettono solo particolari lunghezze d'onda, e non altre? Qual è il meccanismo, per così dire intrinseco, in base al quale il sodio emette solo luce di lunghezza d'onda tipica del colore giallo, per cui Gandalf con il sodio può fabbricare solo fuochi artificiali di colore giallo e non, ad esempio, di colore verde? Per tutto il XIX secolo, tale domanda rimase senza risposta, a causa della nostra ignoranza circa la struttura intima della materia. Un primo, timido passo lo fece nel 1885 il fisico svizzero Johann Jakob Balmer (1825-1898), insegnante liceale, il quale con pazienza certosina cercò una possibile regolarità nella distribuzione di tali lunghezze d'onda nello spettro di emissione dell'idrogeno, ed elaborò la formula seguente, passata alla storia appunto come formula di Balmer:
in essa R è una costante determinata sperimentalmente dallo svedese Johannes Robert Rydberg (1854-1919), e detta per questo Costante di Rydberg, ed n è un numero intero maggiore di 2. Al variare di n, si trovano le frequenze di quelle che vengono solitamente chiamate le righe della "serie di Balmer", cioè quelle nella regione della luce visibile. Da notare che si tratta di una legge empirica, cioè dedotta dall'analisi dei dati sperimentali, non per via teorica da altre già consolidate leggi fisiche. Il valore più attendibile della costante di Rydberg, trovato attraverso numerosissime misurazioni successive, è:
R = 1,097 x 107 m–1
In seguito altri epigoni di Balmer trovarono formule analoghe per esprimere le righe spettrali dell'idrogeno nelle regioni dell'infrarosso e dell'ultravioletto: Theodore Lyman (1874-1954) nel 1906 elaborò una legge che esprimeva la regolarità delle righe spettrali ultraviolette emesse dall'idrogeno attraversato da una corrente elettrica, mentre il tedesco Friedrich Paschen (1865-1947) nel 1908, l'americano Frederick Brackett (1896-1988) nel 1922, l'americano August Herman Pfund (1879-1949) nel 1924 e l'americano Curtis Judson Humphreys (1898-1986) nel 1953 ne scoprirono altrettante nell'infrarosso, via via sempre più lontano. Tutte quante però derivano da generalizzazioni della (1) del tipo:
Se in essa si pone:
m = 1 ed n = 2, 3, 4, 5... si ottiene la serie di Lyman;
m = 2 ed n = 3, 4, 5, 6... si ottiene la serie di Balmer;
m = 3 ed n = 4, 5, 6, 7... si ottiene la serie di Paschen;
m = 4 ed n = 5, 6, 7, 8... si ottiene la serie di Brackett;
m = 5 ed n = 6, 7, 8, 9... si ottiene la serie di Pfund;
m = 6 ed n = 7, 8, 9, 10... si ottiene la serie di Humphreys;
e così via (le serie per valori superiori di m sono senza nome e difficilissime da osservare). In pratica, tutte le lunghezze d'onda delle righe spettrali dell'idrogeno si possono esprimere attraverso la differenza di due termini, detti termini spettrali, di cui il primo è costante del tipo R/m2, ed il secondo è variabile del tipo R/n2. Questo, detto Principio di Combinazione, fu enunciato per la prima volta dal fisico svizzero Walter Ritz (1878-1909): esso afferma che è possibile ricavare l'inverso della lunghezza d'onda di una data riga spettrale, combinando tra loro opportunamente gli inversi delle lunghezze d'onda di altre due righe dello spettro. Per elementi diversi dall'idrogeno, la (2) mantiene la sua validità, anche se cambia il valore della costante R. Trovate per tentativi, a lungo le formule (1) e (2) rimasero solo un procedimento mnemonico per ricavare le righe spettrali dell'idrogeno, ma acquistò un significato fisico proprio grazie alle ricerche di Niels Bohr.

Le diverse serie nelle righe spettrali dell'idrogeno

Consideriamo un atomo di idrogeno. Secondo il modello di Rutherford, esso è formato da un nucleo dotato di carica positiva uguale a quella dell'unico elettrone che gli ruota attorno. La forza responsabile di questo moto è quella elettrostatica, con cui il nucleo e l'elettrone si attraggono, e che è espressa dalla Legge di Coulomb:
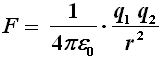
dove q1 e q2 sono le due cariche che si attraggono, r è la loro distanza ed ε è la costante dielettrica del vuoto, pari ad 8,859 x 10–12 N m2/C2. Nel nostro caso, le due cariche sono quelle del protone e dell'elettrone, cioè + e e – e, ed r è il raggio dell'orbita, per cui la precedente diventa:
Poiché la forza F espressa dalla (3) è dello stesso tipo della forza gravitazionale che determina il moto dei pianeti intorno al Sole (vedi in proposito un altro mio ipertesto), se ne conclude che anche il moto dell'elettrone attorno al nucleo di idrogeno è dello stesso tipo. La traiettoria dell'elettrone attorno al nucleo, quindi, dovrebbe essere ellittica. Per semplificare i calcoli, supponiamo che sia circolare, come si fa anche in molti casi in cui si studia la gravitazione. Il moto dell'elettrone allora sarà circolare uniforme. Se m è la massa dell'elettrone, v la sua velocità ed a l'accelerazione centripeta, potremo scrivere:
Il segno meno della (3) e della (4) indica che sia la forza agente sull'elettrone, sia la sua accelerazione centripeta, sono dirette verso il centro del nucleo. Uguagliando le due formule si ha:
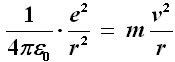
Dalla quale si ricava:
Passiamo ora ad una descrizione in termini di energia. L'energia potenziale dell'elettrone nel campo generato da nucleo è dato dalla formula:
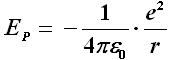
E siccome l'energia totale Etot dell'elettrone è dato dalla somma della sua energia cinetica e della sua energia potenziale, potremo scrivere:
Sostituiamo la (5) nella (6) al posto di m v2. Si ottiene così:
Supponendo che il nucleo sia fermo, quest'ultima esprime l'energia totale dell'atomo, energia che, a causa del segno meno, aumenta all'aumentare della distanza dell'elettrone dal nucleo.
A questo punto Bohr avanzò l'ipotesi fondamentale del suo modello: le orbite dell'elettrone sono quantizzate, cioè l'elettrone può ruotare intorno al nucleo solo su quelle orbite per le quali il momento angolare è un multiplo di h/2π.
Questa ipotesi può sembrare bizzarra, ma essa ha un senso ben preciso, come si evince attraverso un'analisi delle dimensioni fisiche della costante h di Planck, chiamata anche quanto di azione. Noi sappiamo infatti che Planck introdusse la costante h in modo che l'energia E fosse legata alla frequenza f dalla formula E = h f. L'energia si misura in Joule, pari a metro al quadrato per chilogrammo al secondo al quadrato, mentre la frequenza in Hertz, pari a secondi alla meno uno. Si ricava perciò:
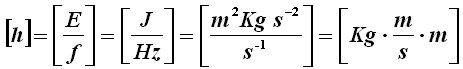
Siccome il momento angolare dell'elettrone rispetto al nucleo è dato da m v r (massa dell'elettrone per la sua velocità per la sua distanza dal nucleo), e quindi si misura in chilogrammi per metro al secondo per metro, se ne deduce che la costante di Planck ha le dimensioni fisiche di un momento angolare; dato che quest'ultimo nell'ottocento era chiamato anche "azione", da qui deriva il nome di "quanto di azione". Su queste basi, l'ipotesi di Bohr significa che sono permesse solo quelle orbite il cui raggio r è tale che:
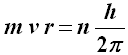 con n = 1, 2, 3...
con n = 1, 2, 3...
La presenza del 2π si giustifica tenendo conto della cosiddetta ipotesi di de Broglie, della quale riparleremo più avanti. Ricavando v da quest'ultima e sostituendola nella (5) si trova:
Questo ci dice che anche il raggio delle orbite risulta quantizzato! In altre parole, non può assumere valori qualsiasi, ma solo quelli che si ottengono sostituendo nella (8) valori interi di n. Sostituendo nella precedente i valori delle costanti fisiche e ponendo n = 1, si ha il raggio di quella che viene chiamata la prima orbita di Bohr, che vale r1 = 0,53 x 10–10 m. La (8) ci dice anche che l'n-esima orbita di Bohr ha raggio espresso dalla semplicissima formula:
![]()
cioè i raggi sono direttamente proporzionali ai quadrati del numero n. Sostituiamo ora la (8) nella (7); con facili calcoli si ottiene:
Ma allora anche l'energia totale dell'elettrone è quantizzata, e precisamente è inversamente proporzionale al quadrato di n. Questo si può anche esprimere affermando che i livelli energetici dell'atomo rappresentano un insieme discreto; n si chiama il numero quantico principale, perchè quantizza l'energia delle orbite, e quindi i loro raggi. Spesso le orbite stazionarie, nelle quali secondo Bohr l'elettrone può ruotare senza perdere energia, anziché essere designate con il numero quantico principale, per motivi storici sono indicate con le lettere maiuscole K, L, M, N, O, P, Q, corrispondenti rispettivamente ai valori 1, 2, 3, 4, 5, 6, 7 di n. Andando da K verso Q, l'energia dello stato stazionario aumenta, pur conservando il segno negativo. Il valore zero è assunto per n tendente all'infinito, cioè praticamente quando l'elettrone si trova a una distanza dal nucleo tale, che l'attrazione coulombiana da parte di esso diventa trascurabile.
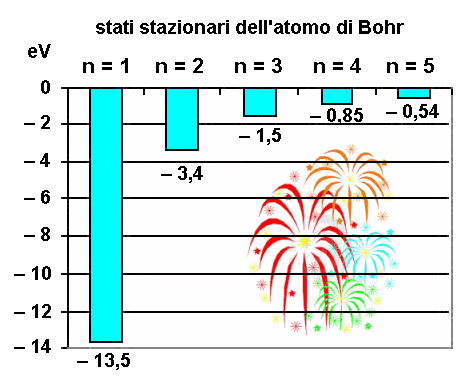
Sostituendo i valori delle costanti fisiche e ponendo n = 1, si ottiene l'energia dell'elettrone nella prima orbita di Bohr. Tale energia è detta energia di prima ionizzazione, perchè è quella necessaria per spostare l'elettrone dalla prima orbita di Bohr fino all'infinito, cioè praticamente fuori dall'atomo, e un atomo privato di un elettrone si dice ionizzato. Essa vale:
E1 = – 2,166 x 10–18 J = – 13,5 eV
dove l'elettronVolt è l'unità di misura dell'energia su scala atomica (1 eV = 1,6 x 10–19 J). I valori di energia corrispondenti ai successivi livelli energetici si trovano a partire da E1 con la semplice formula:
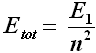
Affermare che il livello K dell'atomo d'idrogeno ha energia pari a – 13,5 eV significa dunque affermare che occorrono 13,5 eV (cioè 2,166 x 10–18 J) per ionizzarlo, ovvero per prendere un elettrone posto su tale livello e portarlo fuori dal raggio d'azione del nucleo. Il livello L (con n = 2) avrà energia pari a – 13,5/4 = – 3,4 eV , e questa sarà l'energia di seconda ionizzazione, cioè occorreranno 3,4 eV (cioè 5,415 x 10–19 J) per portare un elettrone dal livello L all'infinito. Il livello M (con n = 3) avrà energia – 13,5/9 = – 1,5 eV , il livello N (con n = 4) avrà energia – 13,5/16 = – 0,85 eV , e così via. Questi livelli energetici vengono chiamati anche gusci, in inglese shell, da cui il nome di "modello atomico a shell" assegnato all'atomo di Bohr. In cosa questo modello differisce dall'atomo di Rutherford? Nel fatto che l'elettrone non può ruotare attorno al nucleo lungo orbite qualsiasi, perchè in tal caso (come detto) perderebbe tutto la propria energia irraggiandola nello spazio sotto forma di onde elettromagnetiche, ma solo dentro particolari "gusci" nel cui ambito le orbite sono stazionarie, cioè l'elettrone non irradia energia. Solo quando un elettrone "salta" da un livello ad un altro, si ha una variazione dell'energia dell'elettrone stesso. In particolare, se questa transizione avviene da un'orbita più esterna ad una più interna, l'atomo emette un fotone, la cui energia h f è pari alla differenza fra l'energia dello stato di partenza e quella dello stato finale. Ora, supponiamo di aver scaldato un campione, che nel caso del "Signore degli Anelli" sarà la polvere pirica dei fuochi di artificio lanciati da Gandalf durante la festa in onore di Bilbo. L'energia attribuita all'atomo dalla reazione di combustione farà saltare gli elettroni dal loro stato originario ad uno "stato eccitato", dove l'energia sarà maggiore. Ma l'elettrone non può rimanere a lungo su tale stato eccitato; ne consegue che esso tende a ritornare sul suo livello di partenza. La differenza di energia fra i due livelli non va certo perduta, ma viene riemessa sotto forma di un fotone. Detto m il numero quantico dello stato di partenza ed n quello dello stato di arrivo, la frequenza f del fotone sarà data da:
h f = Em – En
Em ed En possono essere ricavate dalla (9). Sostituendo i loro valori nella precedente, si ha:
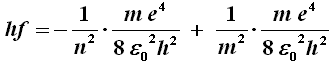
che si può riscrivere:
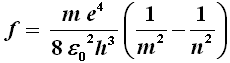
E siccome v = λ f, se ne può ricavare la lunghezza d'onda:
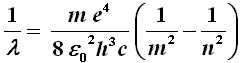
E questa è precisamente la (2), nella quale si pone:
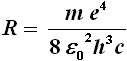
Sostituendo in quest'ultima i valori delle costanti fisiche, Bohr trovò precisamente il valore della costante di Rydberg da noi fornito sopra! In tal modo, appare evidente come spiegare le righe spettrali discrete osservate nello spettro di emissione dell'idrogeno. Dentro l'atomo, secondo il modello di Bohr, sono possibili solo ben determinati livelli energetici, corrispondenti ai valori di m = 1, 2, 3, 4... Ma allora, sono permessi solo un determinato numero di "salti" da un livello all'altro. Come si vede qui sotto, ponendo m = 1 abbiamo i salti da tutti i livelli successivi fino al primo, le cui lunghezze d'onda in nanometri sono indicate accanto ad ogni possibile salto; e questa è precisamente la serie di Lyman, le cui lunghezze d'onda sono minori di quelle della luce rossa, e quindi sono tipiche dell'infrarosso. Se m = 2, la (2) si trasforma nella (1), abbiamo tutti i salti dai livelli successivi fino al secondo, e otteniamo le lunghezze d'onda tipiche della serie di Balmer, che si trovano nella luce visibile, e perciò sono state le prime ad essere osservate. Se m = 3, abbiamo i salti dai livelli successivi sino al terzo, corrispondenti alla serie di Paschen, e i calcoli forniscono lunghezze d'onda tipiche dell'ultravioletto vicino. Allo stesso modo, anche se non li ho indicati in figura, se m = 4 abbiamo i salti dai livelli successivi sino al quarto, e otteniamo la serie di Brackett; se m = 5 abbiamo i salti dai livelli successivi sino al quinto, e otteniamo la serie di Pfund; se m = 6, abbiamo i salti dai livelli successivi sino al quinto, e otteniamo la serie di Humphreys, tutte con le lunghezze d'onda tipiche dell'ultravioletto sempre più lontano. Tutte le transizioni che conducono al medesimo livello finale formano dunque una serie spettrale. Tuttavia, più si alza m, più rari saranno i salti che gli elettroni compiranno, poiché l'energia dovrà essere sempre maggiore, e le righe spettrali corrispondenti saranno più tenui, fino a sparire. Per spiegare i magnifici colori dei fuochi d'artificio osservati dagli Hobbit, basterà la serie di Balmer, quella nel visibile.
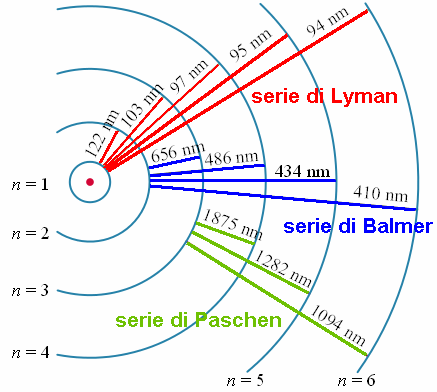
Abbiamo dunque scoperto che i colori dei fuochi artificiali in onore di Bilbo sono costituiti da luce che proviene... da dentro l'atomo! Balmer aveva introdotto nella (2) la R come un fattore empirico di proporzionalità, e noi siamo riusciti, sulla scorta dell'ipotesi di Bohr, a fornire un preciso significato fisico a tale costante e alla legge in cui essa compare. Se ne conclude che solo con l'ipotesi secondo cui l'energia è quantizzata, è possibile fornire le basi razionali per spiegare le osservazioni spettroscopiche, e con esse anche i colori dei magnifici fuochi d'artificio di cui Gandalf era maestro.
Naturalmente, però, lo Stregone non ha certo usato idrogeno nei propri spettacoli pirotecnici. Infatti, tra tutte le frequenze da noi calcolate e riportate nell'immagine soprastante, solo cinque valori, tutti appartenenti alla serie di Balmer, ricadono nella luce visibile; e agli Hobbit non sarebbe certo piaciuto uno spettacolo di raggi infrarossi o ultravioletti giacché, per quanto ne sappiamo, il loro occhio e il loro cervello erano in grado di distinguere le stesse frequenze che osserviamo noi, dal rosso al violetto, e precisamente da 390 a 760 nanometri. I cinque valori ricavabili dalla (1) e compresi entro questo spettro sono Hα = 656 nm, Hβ = 486 nm, Hγ = 434 nm, Hδ = 410 nm ed Hε = 397 nm; la H sta per idrogeno, e le lettere greche progressive α, β, γ, δ, ε corrispondono ai valori 1, 2, 3, 4, 5 di m. Come si vede nella figura sottostante, la riga detta Hα, che corrisponde alla transizione da n = 3 ad m = 2, corrisponde alla luce rossa ed è una delle più frequenti nell'universo a causa dell'abbondanza in esso dell'idrogeno: è estremamente brillante in moltissimi oggetti astronomici, e contribuisce a conferire loro un colore tendente al rosso. La riga Hβ (da n = 4 ad m = 2) ricade invece nel verde, le righe Hγ (da n = 5 ad m = 2), Hδ (da n = 6 ad m = 2) ed Hε (da n = 7 ad m = 2) nel violetto; le righe oltre quest'ultima transizione invece ricadono nella banda ultravioletta dello spettro. Se ne conclude che Gandalf ha dovuto fare ricorso ad altri elementi chimici, per ottenere ad esempio petardi di colorazione gialla o azzurra. Il giallo proviene probabilmente dal sodio, il cui spettro nel visibile presenta un'unica riga gialla a 599 nm.

Nel 1914 i tedeschi James Franck (1882-1964) e Gustav Ludwig Hertz (1887 -1975, nipote del famoso Heinrich Rudolf Hertz, cui è intitolata l'unità di misura della frequenza) condussero un famosissimo esperimento, oggi noto come esperienza di Franck ed Hertz, grazie al quale scoprirono che gli elettroni, attraversando dei vapori di mercurio, subiscono una perdita di energia secondo "livelli" discreti, e che a tale perdita di energia corrisponde una emissione di radiazioni ultraviolette con lunghezza d'onda di 254 nm da parte del mercurio. L'apparato sperimentale è quello visibile qui sotto. Tra il filamento emittente F e la griglia G viene applicata una differenza di potenziale variabile. Tra la griglia G ed il collettore C viene applicata una differenza di potenziale costante di segno opposto di -1,5 V che esercita un’azione frenante, in modo che solo gli elettroni che hanno acquistato una sufficiente energia cinetica sono in grado di raggiungere il collettore C e contribuire alla circolazione di corrente. Finché la differenza di potenziale è inferiore a 4,9 V gli elettroni urtano gli atomi di mercurio con urti elastici, senza cedere energia e, attraversata la griglia, possiedono sufficiente energia per raggiungere il collettore e generare una corrente elettrica, come indica l'amperometro. In corrispondenza di una tensione di 4,9 V gli elettroni hanno sufficiente energia per eccitare gli atomi di mercurio, che emettono una riga spettrale nell’ultravioletto a 254 nm. La cessione di energia agli atomi di mercurio rallenta gli elettroni, facendo diminuire l’intensità di corrente al collettore. Aumentando ulteriormente la tensione il fenomeno si ripresenta con regolarità per valori di tensione multipli di 4,9 V. Infatti, in corrispondenza di una tensione doppia (9,8 V) un elettrone ha sufficiente energia per eccitare in successione due atomi di mercurio, mentre con una tensione tripla (14,7 V) può eccitarne tre e così via. In seguito Niels Bohr si rese conto che si trattava di una chiara conferma della validità del suo modello atomico quantizzato.

Inoltre, la teoria di Bohr dell'atomo di idrogeno riesce ad interpretare gli spettri atomici più semplici; ad esempio, osservando lo spettro dell'idrogeno ad alta risoluzione, si scopre che la riga Hα, proprio una delle più comuni, è in realtà costituita da un doppietto, cioè da due righe estremamente vicine tra di loro, che il modello di Bohr come lo abbiamo descritto qui sopra non è in grado di interpretare. Molte altre righe, se risolte con strumenti di elevatissima sensibilità, mostrano una configurazione ancora più complessa (tripletti, quadripletti...), rappresentate da un certo numero di righe tra loro vicinissime, anche se con frequenza lievemente diversa. Per esempio, la riga gialla del sodio è in realtà formata da un doppietto di righe, le cui lunghezze d'onda differiscono solo di 0,6 nanometri. Si parla in tal caso di struttura fine dello spettro dell'idrogeno. Per poter ricavare tutte le frequenze delle righe che caratterizzano tale struttura fine, è necessario perfezionare il modello di Bohr introducendo altri numeri quantici. Nel 1915 infatti il tedesco Arnold Sommerfeld (1868-1951), amico e collaboratore di Bohr, migliorò il suo modello introducendo un secondo numero quantico l, detto numero quantico angolare, che quantizzava il momento angolare degli elettroni nell'ambito dello stesso guscio atomico, permettendo solo certi valori dell'eccentricità delle orbite ellittiche, e quindi solo certe forme delle orbite. In seguito i fisici tedeschi Otto Stern (1888-1969) e Walther Gerlach (1889-1979) realizzarono nel 1922 quello che è passato alla storia come esperimento di Stern e Gerlach; esso dimostrò che anche il momento magnetico associato alle orbite elettroniche è quantizzato: facendo passare atomi di argento vaporizzato attraverso un campo magnetico non uniforme, i due scienziati dimostrarono che il fascio di atomi non produce una distribuzione continua sullo schermo di un rivelatore, ma le particelle che passano attraverso il campo magnetico sono deflesse o in alto o in basso di una quantità ben precisa. Di conseguenza anche il momento magnetico può assumere solo valori discreti, e sono possibili solo certi orientamenti spaziali delle orbite. Per questo venne introdotto il terzo numero quantico m o numero quantico magnetico. I primi tre numeri quantici sono legati tra di loro da queste semplici relazioni:
![]()

A questo punto, però, occorre far notare una debolezza intrinseca del modello di atomo fin qui descritto, e noto comunemente con il nome di modello atomico di Bohr-Sommerfeld. Ad accorgersene per primo fu lo stesso Ernest Rutherford, in una lettera datata 20 marzo 1913 che il grande scienziato spedì a Bohr subito dopo la pubblicazione del suo primo lavoro sulla quantizzazione applicata all'atomo di idrogeno. Vale la pena di leggere uno stralcio di quella lettera, contenuta in "I quanti e la vita" dello stesso Bohr:
« Caro dottor Bohr, ho ricevuto il suo lavoro e l'ho letto con grande interesse, ma mi riservo di rivederlo con cura appena ne avrò il tempo. Le sue idee sull'origine dello spettro dell'idrogeno sono molto ingegnose, e sembrano funzionare bene; ma la mescolanza delle idee di Planck con la vecchia meccanica consente molto difficilmente di formarsi un'idea fisica della base di tutto il discorso... »
In un'altra occasione, sempre Rutherford ebbe a dire che non capiva come si potesse usare « la Fisica Classica il lunedì, il mercoledì e il venerdì, e la Fisica dei Quanti il martedì, il giovedì e il sabato ». In altre parole, siccome la quantizzazione espressa dalla formula E = h f non trova nessuna giustificazione nell'elettrodinamica classica, si ha la sensazione di due formulazioni matematiche giustapposte tra loro sebbene risultino incompatibili. Bohr infatti utilizzava la quantizzazione dell'energia introdotta da Planck per giustificare perchè solo certe orbite elettroniche sono ammissibili, ma poi, per calcolare le energie di ogni livello e per derivare la formula di Balmer (2), sfrutta ancora le formule tipiche della Meccanica Classica. Proprio per questo motivo il modello di Bohr-Sommerfeld è oggi noto come modello quantomeccanico, risultante dell'utilizzo contemporaneo della Fisica dei Quanti e della Meccanica di Newton. Questo fatto lasciava una sensazione per dir così di incompletezza, che poteva essere risolta solo dando vita a una formulazione matematica completamente nuova della Fisica Atomica, che prescindesse dalla Fisica Classica, ma la contenesse come caso particolare nel caso di sistemi macroscopici.
Questa riformulazione rappresentò uno dei maggiori sforzi concettuali della scienza di tutti i tempi, e fa parte della rivoluzione scientifica degli anni venti e trenta, che andò a braccetto con la scoperta di una realtà fisica senza la quale imbastire un modello puramente quantistico, e non più quantomecanico, sarebbe stato impossibile. Parliamo del dualismo onda-particella, introdotto per la prima volta nel 1924 dal fisico francese Louis-Victor de Broglie (1892-1987) nell'ambito della sua tesi di laurea. Egli ipotizzò infatti che ogni particella può manifestare anche un comportamento ondulatorio, unificando due concetti che fin qui la Fisica aveva tenuto rigidamente separati. Se è così, anche gli elettroni che orbitano sulle shell di Bohr devono essere associati ad onde, che de Broglie battezzò onde di materia. Siccome un'onda di energia E deve avere una frequenza f = E / h, de Broglie ebbe l'idea di associare all'onda una particella avente quantità di moto p pari a E / c = h f / c = h / λ. Viceversa, ad una particella con quantità di moto p si può associare un'onda avente lunghezza d'onda λ = h / p. Tuttavia, gli elettroni sulle orbite di Bohr si muovono lungo orbite chiuse, e quindi le onde di materia ad esse associate devono essere giocoforza onde stazionarie. Siccome le onde stazionarie hanno lunghezza d'onda pari ad un sottomultiplo intero della distanza fra gli estremi tra i quali oscillano, se r è il raggio dell'n-esima orbita di Bohr avremo:
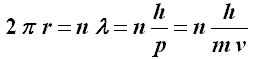
da cui si ricava immediatamente:
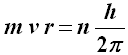
E questa, come abbiamo visto, coincide con l'ipotesi di Bohr alla base del suo modello atomico! Perfino il 2π , che inizialmente ci sembrava comparso quasi per magia, trova piena giustificazione grazie all'ipotesi avanzata da de Broglie.
Naturalmente, una cosa è avanzare un'ipotesi matematica, un'altra è verificarla sperimentalmente in natura. A riuscirci nel 1926 fu George Paget Thomson (1892-1975), figlio del già citato Joseph John Thomson. La vita gioca davvero degli strani scherzi: il padre aveva dimostrato che gli elettroni, costituenti dei raggi catodici, sono particelle; il figlio dimostrò che hanno anche un comportamento ondulatorio! Mentre G.P. Thomson lavorava sugli elettroni in Inghilterra, negli Stati Uniti Clinton Joseph Davisson (1881-1958) e Lester Halbert Germer (1896-1971), contemporaneamente e indipendentemente, ottennero una figura di diffrazione di elettroni attraverso il reticolo cristallino di una lamina di nichel, la cosiddetta Esperienza di Davisson e Germer. La teoria di de Broglie trovò così una clamorosa e inaspettata verifica sperimentale.
Lavorando sul dualismo onda-particella, nel 1926 il grande fisico teorico austriaco Erwin Schrödinger (1887-1961) riuscì infine ad elaborare un'equazione che permette di descrivere l'evoluzione nel tempo di ogni sistema microscopico e perciò legato al mondo dei quanti, indipendentemente dai postulati della Fisica Classica. Tale equazione, descritta nell'articolo "Quantisierung als Eigenwertproblem" ("Quantizzazione come problema agli autovalori"), rappresenta l'equivalente quantistico del Principio Classico di Conservazione dell'Energia Meccanica Totale, ed oggi è universalmente nota come Equazione di Schrödinger. Potete vederla, nella sua scrittura più comune, in questo fotomontaggio sopra il desolato panorama di Mordor, visto che risolverla è quasi altrettanto complicato quanto attraversare quell'inospitale regione a piedi, come hanno fatto Frodo e Sam:
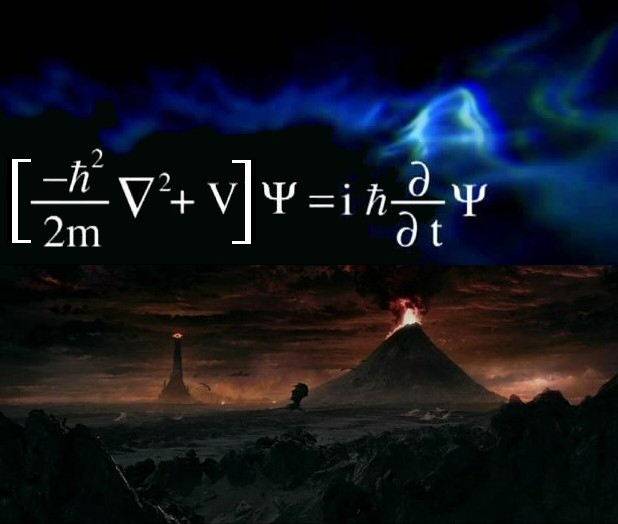
In essa, Ψ è la cosiddetta "funzione d'onda", che descrive lo stato fisico dell'onda di materia associata ad ogni sistema quantistico. Si tratta di una complicatissima equazione differenziale alle derivate parziali, e noi non ne affronteremo lo studio in questa sede, andando ben al di là delle finalità di questo ipertesto. Basti dire che essa può essere applicata anche all'atomo di idrogeno. Risolvendola, con non poche difficoltà matematiche, da essa emergono spontaneamente i tre numeri quantici n, l, m che noi abbiamo incontrato in quel che precede. Ne consegue che la quantizzazione (rispettivamente dell'energia, del momento angolare e del momento magnetico dell'elettrone) non è un mero escamotage matematico per risolvere un problema altrimenti insolubile, ma rappresenta una realtà fisica che emerge in modo naturale dallo studio della Meccanica Quantistica, la nuova branca della Fisica che ha sostituito la Meccanica di Newton nell'analisi dei sistemi microscopici. Questo elegante risultato ha però un prezzo, rappresentato dal cosiddetto Principio di Indeterminazione di Heisenberg, dal nome del fisico tedesco Werner Heisenberg (1901-1976) che è considerato con Schrödinger il fondatore della Meccanica Quantistica, avendo elaborato nel 1925 la Meccanica delle Matrici, la prima (complicatissima) formalizzazione di tale nuova meccanica. In base a tale principio, non è possibile misurare simultaneamente due grandezze fisiche tra loro coniugate (posizione e quantità di moto, oppure energia e tempo) con precisione grande a piacere: minore sarà l'incertezza sulla misura della prima, maggiore sarà l'incertezza sulla misura della seconda. Ne consegue che, all'interno dell'atomo, io non posso conoscere con grande precisione sia la posizione che la quantità di moto (e quindi la velocità) di un elettrone. Quest'ultimo dunque non si muove su un'orbita classicamente intesa: il concetto di traiettoria del punto materiale, che è alla base della Meccanica di Galilei e Newton, nel mondo quantistico semplicemente perde di senso.
A Max Born (1892-1970), allievo del famosissimo matematico David Hilbert, è attribuita la cosiddetta interpretazione probabilistica della Meccanica Quantistica, in base alla quale la funzione d'onda Ψ viene ad avere un preciso significato fisico. Siccome gli elettroni si comportano sia come onde che come particelle, in presenza di una fenditura opportunamente piccola un elettrone deve "diffrangere" attraverso di essa, nel senso che l'onda di materia descritta dalla funzione d'onda Ψ si "distribuisce" nello spazio al di là della fenditura. Schrödinger inizialmente pensava che l'elettrone effettivamente si "sciogliesse" al di là della fenditura, distribuendosi nello spazio, ma Max Born rifiutò tale concezione come "metafisica", ed affermò piuttosto che il quadrato del modulo della funzione d'onda, cioè |Ψ|2, rappresenta la probabilità (più precisamente la densità di probabilità, essendo spazio e tempo variabili continue) di trovare l'elettrone al di là della fenditura. Se insomma io mando un fascio di un milione di elettroni verso la fenditura, la maggior parte delle particelle al di là di essa si distribuirà nello spazio in modo da "disegnare" una figura di diffrazione. Dove Ψ assume valori più elevati, la figura risulta più marcata, perchè lì è più probabile trovare elettroni! Di conseguenza il concetto di "orbita" dell'elettrone intorno al nucleo va sostituito con quello di orbitale, inteso come la regione dove è più probabile individuare l'elettrone intorno al nucleo.
Questa concezione probabilistica della nuova Meccanica dei Quanti si attirò fin dal principio ogni sorta di critiche. Albert Einstein non la accettò mai, e sintetizzò la sua opposizione ad essa nel celeberrimo aforisma "Gott würfelt nicht" ("Dio non gioca a dadi"). Inoltre, se applicata a fenomeni che hanno rilevanza anche nel mondo macroscopico, essa conduce a risultati assolutamente stravaganti. Per comprendere il perchè, rileggiamo insieme le ultime righe de « Le Due Torri »:
«
Sam urlò brandendo Pungolo, ma la sua piccola voce si perse nel tumulto.
Nessuno si accorse di lui. La grande porta si chiuse fragorosamente. Bum. Le
sbarre di ferro la sprangarono. Clang. Il cancello era serrato. Sam si
scaraventò contro le impenetrabili lamine d'ottone e cadde a terra privo di
sensi. »
(SdA, libro
IV, cap. X)
Com'è logico, gettandosi contro il portone della Torre di Cirith Ungol, il povero Mastro Samvise rimbalza indietro, e non ha alcuna speranza di attraversarne lo spesso strato di metallo. Ma ciò avviene perchè egli non obbedisce alle leggi della Meccanica Quantistica, bensì a quelle della Meccanica Quotidiana. Risolvendo invece l'equazione di Schrödinger per un elettrone accelerato verso una barriera di potenziale, scopriamo che esso può anche essere trovato dall'altra parte della barriera, nel senso che la sua funzione d'onda Ψ può avere valori non nulli anche al di là di essa. Ciò si esprime dicendo ad esempio che l'elettrone ha il 65 % di probabilità di essere riflesso dalla barriera e il 35 % di essere trasmesso al di là di essa: tale comportamento piuttosto bizzarro va sotto il nome di effetto tunnel. In tal modo, un sistema quantistico può trovarsi in più stati diversi contemporaneamente, ciascuno con la sua probabilità. Un esempio di questo fatto può essere formulato, nell'ambito del Legendarium di Tolkien, facendo ricorso ad una celeberrima affermazione del Grigio Pellegrino, riferita da Faramir a Frodo, nella quale egli elenca tutti i nomi con cui è conosciuto:
« Molti i nomi che ho nelle diverse terre. Mithrandir sono per gli Elfi, Tharkûn per i Nani; Olòrin ero da giovane nell'ormai obliato Ovest, nel Sud Incànus, nel Nord Gandalf; nell'Est non vado mai. »
(SdA, libro
IV, cap. V)
È come se egli affermasse
di essere contemporaneamente Mithrandir, Tharkûn, Olòrin, Incànus e Gandalf,
ciascuno con una sua probabilità: se nella sua vita (poniamo) è stato per il
25 % del tempo fra gli Elfi, per il 10 % tra i Nani, per il 30 % nell'obliato
Ovest, per il 5 % al Sud e per il 30 % al Nord, lo "stato quantico"
dello  Stregone può
essere descritto come formato simultaneamente da un 25 % di Mithrandir, da un
10 % di Tharkûn, da un 30 % di Olòrin, da un 5 % di Incànus e da un 30 % di
Gandalf. Dato che all'Est non va mai, la percentuale dello stato "Gandalf
ad est" è zero. Consideriamo tuttavia il celeberrimo esempio, adattato
all'universo di Tolkien, di un orchetto posto in una stanza insieme a una
bottiglia chiusa contenente un gas velenosissimo, la cui apertura è comandata
dal decadimento di un isotopo radioattivo, un fenomeno eminentemente di natura
quantistica. Se l'isotopo ha il 60 % di probabilità di decadere e il 40 % di
probabilità di non farlo, ne consegue che anche l'orchetto allo stesso tempo
sarà per il 60 % vivo, e per il 40 % morto!
(nell'originale era stato usato un gatto, per cui si parla comunemente del Paradosso
del Gatto di Schrödinger. Esso è entrato nell'immaginario collettivo
e ha dato vita a non poche parodie, come mostra l'immagine scherzosa qui a
fianco)
Stregone può
essere descritto come formato simultaneamente da un 25 % di Mithrandir, da un
10 % di Tharkûn, da un 30 % di Olòrin, da un 5 % di Incànus e da un 30 % di
Gandalf. Dato che all'Est non va mai, la percentuale dello stato "Gandalf
ad est" è zero. Consideriamo tuttavia il celeberrimo esempio, adattato
all'universo di Tolkien, di un orchetto posto in una stanza insieme a una
bottiglia chiusa contenente un gas velenosissimo, la cui apertura è comandata
dal decadimento di un isotopo radioattivo, un fenomeno eminentemente di natura
quantistica. Se l'isotopo ha il 60 % di probabilità di decadere e il 40 % di
probabilità di non farlo, ne consegue che anche l'orchetto allo stesso tempo
sarà per il 60 % vivo, e per il 40 % morto!
(nell'originale era stato usato un gatto, per cui si parla comunemente del Paradosso
del Gatto di Schrödinger. Esso è entrato nell'immaginario collettivo
e ha dato vita a non poche parodie, come mostra l'immagine scherzosa qui a
fianco)
Per risolvere il Paradosso dell'"Orchetto di Schrödinger", come potremmo definire la nostra versione dell'esperimento mentale testé descritto, sono state proposte diverse soluzioni. Niels Bohr (sua è la celebre "Interpretazione di Copenaghen") suggeriva che è l'osservazione a far "collassare" il sistema su una delle due possibilità quantistiche. In altre parole, quando apro la stanza mi rendo conto se l'orchetto è vivo (per la precisione, al 100 % vivo e allo 0 % morto) o defunto (per la precisione, allo 0 % vivo e al 100 % morto). Infatti, nella Meccanica Quantistica l'osservatore interagisce con l'osservazione: se voglio conoscere la posizione esatta di un elettrone, devo illuminarlo, ma i fotoni con cui lo illumino hanno energia paragonabile a quella dell'elettrone, ed allora ne perturbano la quantità di moto, rendendo quest'ultima inosservabile con precisione. Ma allora a determinare la vita o la morte dell'orchetto non è l'isotopo, bensì l'osservatore! Per risolvere questo ulteriore paradosso, Hugh Everett III (1930 -1982) nel 1957 propose la cosiddetta Interpretazione a Molti Mondi. Ogni volta che uno stato quantico può presentarsi in due o più modalità, si generano altrettanti mondi diversi. Nel nostro caso, avremo due mondi paralleli, uno nel quale l'orchetto è vivo, l'altro in cui esso è deceduto. La maggior parte dei fisici all'epoca respinse tale interpretazione giudicandola fantascientifica, ma nel tempo essa ha raccolto un numero sempre crescente di consensi, anche se introducendo delle varianti, come hanno fatto Murray Gell-Mann (1929-) e David Deutsch (1953-).
Prima di chiudere questa lezione dedicata alla Meccanica Quantistica, occorre accennare ad un ultimo argomento; i numeri quantici che caratterizzano gli elettroni negli atomi, infatti, non sono tre, ma quattro. Il quarto è chiamato numero quantico di spin s, e venne introdotto nel 1924 da Wolfgang Pauli (1900-1958) per spiegare alcune anomalie nelle righe spettrali degli elementi alcalini (litio, sodio, potassio, cesio, rubidio e francio) che non erano interpretabili usando solo i primi tre numeri quantici. Pauli si convinse che era necessario aggiungere quello che chiamò un "grado di libertà quantico a due valori", cioè un ulteriore numero quantico che potesse assumere solo due valori possibili. Come interpretare fisicamente questo ulteriore grado di libertà? Due giovani fisici olandesi, George Uhlenbeck (1900-1988) e Samuel Goudsmit (1902-1978) proposero che esso fosse legato alla quantizzazione del momento angolare intrinseco dell'elettrone. Già si è detto che l'elettrone possiede un momento angolare orbitale, dovuto al fatto che ruota attorno al nucleo. Se però immaginiamo l'elettrone come una piccolissima sfera conduttrice con la carica negativa distribuita sulla sua superficie, possiamo pensare che esso ruoti anche attorno al proprio asse, così come la Terra gira sia intorno al proprio asse che attorno al Sole. Tale movimento di rotazione porta un ulteriore contributo al momento angolare, contributo detto di "spin" (dall'inglese "trottola"), che può assumere solo due valori, se si ipotizza che l'elettrone giri intorno a se stesso con velocità costante, in senso antiorario oppure orario, e quindi con l'asse di rotazione rivolto verso l'alto (up) oppure verso il basso (down), come nella figura a fianco. Per questo si parla di "spin up" e "spin down". Il momento angolare risultò poter avere i due valori possibili + 1/2 h/ 2π oppure –1/2 h/ 2π , da cui si deducono i due possibili valori ± 1/2 del numero quantico s.
 Il problema però consiste
nel fatto che, in tutti gli esperimenti in cui si è cercata un'eventuale
struttura interna dell'elettrone attraverso lo scattering, cioè bombardandolo
con altre particelle come aveva fatto Rutherford con gli atomi d'oro, esso
finora si è sempre rivelato perfettamente puntiforme.
Ma allora, come può ruotare su se stessa una particella praticamente priva di
raggio? La risposta corretta fu fornita dal fisico britannico Paul Adrien Maurice Dirac
(1902-1984), che nel 1928 descrisse per la prima volta l'elettrone da un punto
di vista relativistico, cioè tenendo conto del
fatto che esso si muove a una velocità prossima a quella della luce: un
aspetto che Schrödinger ed Heisenberg avevano del tutto trascurato. Egli
scrisse una nuova equazione, oggi universalmente nota come Equazione
di Dirac, che rappresenta una generalizzazione di quella di Schrödinger
per le energie relativistiche, e che gli permise tra l'altro di prevedere
l'esistenza del positrone, cioè l'antiparticella
dell'elettrone, con ugual massa e carica positiva, poi effettivamente scoperta
nel 1932 da Carl David Anderson (1905-1991): era
la prima prova dell'esistenza dell'antimateria.
Orbene, applicando l'equazione di Schrödinger
all'atomo di idrogeno, abbiamo visto come da esso emergano i primi tre
numeri quantici. Applicando invece all'atomo di idrogeno l'equazione di Dirac
e risolvendola, i numeri quantici che ne risultano sono quattro.
In altre parole, derivando da un'equazione che governa i sistemi quantistici e
relativistici, ne consegue che lo spin è un effetto
relativistico! In altre parole, non è legato a una presunta rotazione
dell'elettrone su se stesso, ma è un "momento angolare aggiuntivo"
che va sommato a quello orbitale perchè l'elettrone si muove a una velocità
prossima a quella della luce, e perciò non obbedisce alla dinamica delle
basse energie (classica o quantistica che sia), bensì a quella delle alte
energie. Ad ogni modo, il termine "spin" ormai si era affermato e
non venne modificato. La scoperta del quarto numero quantico peraltro permise
a Wolfgang Pauli di formulare il famoso Principio di
Esclusione, il quale stabilisce che due elettroni distinti all'interno
dello stesso atomo non possono avere i quattro numeri quantici n,
m, l ed s tutti uguali tra di loro.
Tale principio permette di "costruire" la struttura elettronica di
tutti gli atomi della Tavola Periodica di Mendeleev,
a cui proprio Bohr diede una nuova veste, dimostrando che essa rispecchia il
"riempimento" (in tedesco Aufbau) dei
successivi orbitali che circondano un nucleo atomico.
Il problema però consiste
nel fatto che, in tutti gli esperimenti in cui si è cercata un'eventuale
struttura interna dell'elettrone attraverso lo scattering, cioè bombardandolo
con altre particelle come aveva fatto Rutherford con gli atomi d'oro, esso
finora si è sempre rivelato perfettamente puntiforme.
Ma allora, come può ruotare su se stessa una particella praticamente priva di
raggio? La risposta corretta fu fornita dal fisico britannico Paul Adrien Maurice Dirac
(1902-1984), che nel 1928 descrisse per la prima volta l'elettrone da un punto
di vista relativistico, cioè tenendo conto del
fatto che esso si muove a una velocità prossima a quella della luce: un
aspetto che Schrödinger ed Heisenberg avevano del tutto trascurato. Egli
scrisse una nuova equazione, oggi universalmente nota come Equazione
di Dirac, che rappresenta una generalizzazione di quella di Schrödinger
per le energie relativistiche, e che gli permise tra l'altro di prevedere
l'esistenza del positrone, cioè l'antiparticella
dell'elettrone, con ugual massa e carica positiva, poi effettivamente scoperta
nel 1932 da Carl David Anderson (1905-1991): era
la prima prova dell'esistenza dell'antimateria.
Orbene, applicando l'equazione di Schrödinger
all'atomo di idrogeno, abbiamo visto come da esso emergano i primi tre
numeri quantici. Applicando invece all'atomo di idrogeno l'equazione di Dirac
e risolvendola, i numeri quantici che ne risultano sono quattro.
In altre parole, derivando da un'equazione che governa i sistemi quantistici e
relativistici, ne consegue che lo spin è un effetto
relativistico! In altre parole, non è legato a una presunta rotazione
dell'elettrone su se stesso, ma è un "momento angolare aggiuntivo"
che va sommato a quello orbitale perchè l'elettrone si muove a una velocità
prossima a quella della luce, e perciò non obbedisce alla dinamica delle
basse energie (classica o quantistica che sia), bensì a quella delle alte
energie. Ad ogni modo, il termine "spin" ormai si era affermato e
non venne modificato. La scoperta del quarto numero quantico peraltro permise
a Wolfgang Pauli di formulare il famoso Principio di
Esclusione, il quale stabilisce che due elettroni distinti all'interno
dello stesso atomo non possono avere i quattro numeri quantici n,
m, l ed s tutti uguali tra di loro.
Tale principio permette di "costruire" la struttura elettronica di
tutti gli atomi della Tavola Periodica di Mendeleev,
a cui proprio Bohr diede una nuova veste, dimostrando che essa rispecchia il
"riempimento" (in tedesco Aufbau) dei
successivi orbitali che circondano un nucleo atomico.
Infine, le particelle subatomiche vengono oggi classificate in fermioni, che obbediscono alla cosiddetta Statistica di Fermi-Dirac ed hanno spin semintero (ad esempio protoni, elettroni e neutroni), e bosoni, che obbediscono alla cosiddetta Statistica di Bose-Einstein ed hanno spin intero (ad esempio fotoni e particelle alfa). Ma di tutto questo parleremo ampiamente nella prossima lezione, se vorrete seguirmi in questo nostro itinerario, cliccando qui!
![]()