Un versetto poco conosciuto della Bibbia
recita:
« Ed egli fece un mare di
bronzo, largo dieci cubiti da un'estremità all'altra; era di forma rotonda, e
la sua altezza era di cinque cubiti; ed una corda lunga trenta cubiti poteva
farne il giro » (I libro dei Re 7, 23)
 Lo stesso versetto si può ritrovare in II
Cronache, 4,2. Esso fa parte di una lunga lista di arredi del grande Tempio di
Salomone, costruito attorno al 950 a.C. Come si vede, la Bibbia dava a pi greco,
cioè al rapporto tra circonferenza e cerchio, il non precisissimo valore di 3.
Molto prima di Salomone, in Mesopotamia (da cui pure Abramo proveniva) era stato
trovato per
Lo stesso versetto si può ritrovare in II
Cronache, 4,2. Esso fa parte di una lunga lista di arredi del grande Tempio di
Salomone, costruito attorno al 950 a.C. Come si vede, la Bibbia dava a pi greco,
cioè al rapporto tra circonferenza e cerchio, il non precisissimo valore di 3.
Molto prima di Salomone, in Mesopotamia (da cui pure Abramo proveniva) era stato
trovato per  il valore di 25/8 = 3,125. A difesa del passo biblico si
può far notare che la misura è indubbiamente approssimativa e che, essendo la
Bibbia un libro religioso e non un trattato di ingegneria, un'elevata precisione
nelle misure era ritenuta superflua.
il valore di 25/8 = 3,125. A difesa del passo biblico si
può far notare che la misura è indubbiamente approssimativa e che, essendo la
Bibbia un libro religioso e non un trattato di ingegneria, un'elevata precisione
nelle misure era ritenuta superflua.
Nel "Papiro di
Rhind", risalente al 1650 a.C. circa ma forse copia di un testo più
antico, si attribuisce a  il valore di 4 (8/9)2 = 3,16. Il
primo calcolo teorico preciso risale però al greco Archimede
di Siracusa (287-212 a.C.), che ottenne la seguente approssimazione:
il valore di 4 (8/9)2 = 3,16. Il
primo calcolo teorico preciso risale però al greco Archimede
di Siracusa (287-212 a.C.), che ottenne la seguente approssimazione:
223/71 <  < 22/7
< 22/7
Notiamo che Archimede, a differenza
dell'ignoto autore del Papiro di Rhind, aveva capito che  non vale né
223/71 né 22/7, e non fece alcun tentativo per calcolarne l'esatto valore, a
differenza di tanti matematici venuti dopo di lui, e con ben altri strumenti di
calcolo a disposizione. Se prendiamo come valore di pi greco il valore medio
dell'intervallo archimedeo, otteniamo 3,1418, con un errore appena pari a
0,0002. Ecco il ragionamento di Archimede. Consideriamo un cerchio di raggio 1,
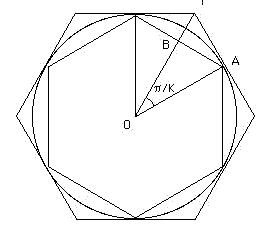
in cui inscriviamo un poligono regolare di 3 * 2n-1 lati, ed a cui
circoscriviamo un poligono regolare di 3 *
2n-1 lati, i cui semiperimetri siano rispettivamente bn ed
an. Il risultato è il diagramma a sinistra.
non vale né
223/71 né 22/7, e non fece alcun tentativo per calcolarne l'esatto valore, a
differenza di tanti matematici venuti dopo di lui, e con ben altri strumenti di
calcolo a disposizione. Se prendiamo come valore di pi greco il valore medio
dell'intervallo archimedeo, otteniamo 3,1418, con un errore appena pari a
0,0002. Ecco il ragionamento di Archimede. Consideriamo un cerchio di raggio 1,
in cui inscriviamo un poligono regolare di 3 * 2n-1 lati, ed a cui
circoscriviamo un poligono regolare di 3 *
2n-1 lati, i cui semiperimetri siano rispettivamente bn ed
an. Il risultato è il diagramma a sinistra.
 Si
ottiene così una successione crescente:
Si
ottiene così una successione crescente:
b1, b2, b3, ...
ed una decrescente:
a1, a2, a3, ...
entrambe queste successioni hanno come limite
il nostro  .
.
Usando la notazione trigonometrica moderna
si ha che i semiperimetri sono dati da:
an = K tg ( /K)
, bn
= K sen (
/K)
, bn
= K sen ( /K)
/K)
dove K = 3 . 2n-1 (vedi figura). Ragionando
analogamente, si ha:
an+1 = 2K tg ( /2K)
, bn+1 = 2K sen (
/2K)
, bn+1 = 2K sen ( /2K)
/2K)
Non è un difficile esercizio di trigonometria
dimostrare che:
(1/an + 1/bn) = 2/an+1
(1)
an+1bn = (bn+1)2
(2)
Archimede, Partendo da a1 = 3 tg
( /3)
= 3
/3)
= 3 3 e b1 = 3 sen
(
3 e b1 = 3 sen
( /3) = 3
/3) = 3 3/2,
calcolò il valore di a2 usando la (1), e quello di b2
usando la (2); trovò poi quello di a3
usando la (1), poi quello di b3 usando la (2), e così via fino a
trovare a6
e b6. La conclusione che egli trasse fu che:
3/2,
calcolò il valore di a2 usando la (1), e quello di b2
usando la (2); trovò poi quello di a3
usando la (1), poi quello di b3 usando la (2), e così via fino a
trovare a6
e b6. La conclusione che egli trasse fu che:
b6 <  < a6.
< a6.
Notiamo che Archimede non possedeva né la
trigonometria né la notazione decimale, entrambe introdotte dagli Arabi nel
Medioevo, per cui egli derivò la (1) e la (2) per via puramente geometrica, e
facendo uso di sole frazioni i cui termini sono numeri interi. Oggi quindi le
sue deduzioni hanno del meraviglioso, e non è degno di meraviglia solo il fatto che
egli si fermò ai poligoni di 96 lati, ma che egli si sia spinto così lontano!
Usando lo stesso metodo di Archimede, e
giungendo fino ai poligoni con 1030 lati, i matematici successivi ne affinarono
i risultati:
| Tolomeo
| (ca. 150 d.C.)
| 3,1416
|
| Tsu Ch'ung
Chi
| (430-501 d.C.)
| 355/113
|
| Al-Khwarizmi
| (ca. 800 )
| 3,1416
|
| Al-Kashi
| (ca. 1430)
| 14 cifre
|
| Viète
| (1540-1603)
| 9 cifre
|
| Roomen
| (1561-1615)
| 17 cifre
|
| Van
Ceulen
| (ca. 1600)
| 35 cifre |
Nel 1699, Sharp
si spinse fino a 71 cifre decimali, usando invece la convergenza di una serie
numerica. Nel 1701, Machin
usò un'altra serie da lui scoperta per sfondare il muro delle 100 cifre
decimali. Nel 1789 Vega
toccò le 126 cifre e le portò a 136 nel 1794. Nel 1873,
Shanks calcolò (a mano!) 707 cifre di
cui 527 esatte. Oggi, con l'uso dei moderni calcolatori digitali, si è giunti
al milione di cifre decimali, e si spera di poter arrivare ancora più in là.
Concludiamo questo capitolo citando un
metodo mnemonico, ideato negli USA, per poter ricordare le prime cifre di  quando ancora non esistevano le calcolatrici tascabili.. Ogni cifra successiva
è data dal numero di lettere di ogni parola della seguente tiritera:
quando ancora non esistevano le calcolatrici tascabili.. Ogni cifra successiva
è data dal numero di lettere di ogni parola della seguente tiritera:
« How I want a drink, alcoholic of course, after the heavy
lectures involving quantum mechanics. All of thy geometry, Herr Planck,
is fairly hard... »
Da cui si ricava 3.14159265358979323846264...
 Lo stesso versetto si può ritrovare in II
Cronache, 4,2. Esso fa parte di una lunga lista di arredi del grande Tempio di
Salomone, costruito attorno al 950 a.C. Come si vede, la Bibbia dava a pi greco,
cioè al rapporto tra circonferenza e cerchio, il non precisissimo valore di 3.
Molto prima di Salomone, in Mesopotamia (da cui pure Abramo proveniva) era stato
trovato per
Lo stesso versetto si può ritrovare in II
Cronache, 4,2. Esso fa parte di una lunga lista di arredi del grande Tempio di
Salomone, costruito attorno al 950 a.C. Come si vede, la Bibbia dava a pi greco,
cioè al rapporto tra circonferenza e cerchio, il non precisissimo valore di 3.
Molto prima di Salomone, in Mesopotamia (da cui pure Abramo proveniva) era stato
trovato per  Si
ottiene così una successione crescente:
Si
ottiene così una successione crescente: