Se
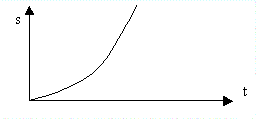
il punto materiale si muove su una traiettoria rettilinea e il modulo della sua
velocità non si mantiene costante nel tempo si parla di moto vario.

Dal grafico (s,t),
calcolando le pendenze delle tangenti nei vari istanti di tempo, si possono
determinare i valori delle velocità istantanee.
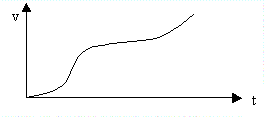
Dal grafico (v,t),
calcolando le pendenze delle tangenti nei vari istanti di tempo, si possono
determinare i valori delle accelerazioni istantanee.
MOTO
UNIFORMEMENTE VARIO
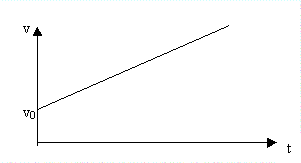
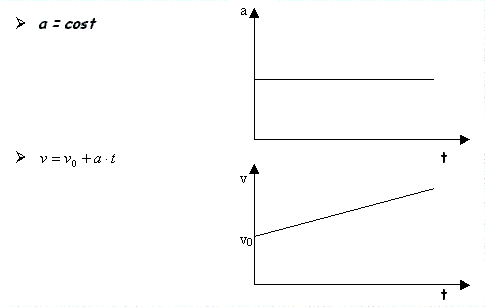
Se il grafico (v,t) è rappresentato da
una retta non orizzontale, la velocità varia linearmente nel tempo: la tangente
al grafico in ciascun punto è la retta stessa, il cui coefficiente angolare,
costante, dà il valore dell’accelerazione che caratterizza il moto, che si
dice uniformemente vario.
In particolare, se a > 0 si
parla di moto uniformemente accelerato, se a < 0 di moto uniformemente
decelerato.
LEGGE
DELLE VELOCITA’
Per un moto ad accelerazione costante,
l’accelerazione istantanea coincide con l’accelerazione media relativa a
qualunque intervallo di tempo considerato. Se il corpo, partito nell’istante t0
con velocità iniziale v0 , possiede nell’istante di
tempo t la velocità v si può scrivere:
![]()
dove
![]() e
e
![]() .
.
Ne
segue che:
![]()
Se
supponiamo di iniziare l’osservazione del moto nell’istante di tempo t0
, allora, nel nostro caso, è t0 = 0.
Di
conseguenza la relazione precedente diventa:
![]()
LEGGE
ORARIA
Consideriamo sempre lo stesso corpo,
partito nell’istante t0 con velocità iniziale v0
dalla posizione s0, e che occupa nell’istante di tempo t
la posizione s con velocità v.
Il moto del corpo, in realtà
uniformemente vario, può essere assimilato a un moto rettilineo uniforme,
caratterizzato da una velocità media data dalla media aritmetica delle velocità
iniziale e finale del corpo:
![]()
La legge oraria del moto è dunque:
![]()
Tenendo conto, poi, della legge delle
velocità
![]() , e inserendo tale relazione nella precedente si ha:
, e inserendo tale relazione nella precedente si ha:
![]()
Questa
relazione fornisce il legame esplicito tra la posizione assunta dal corpo e il
tempo, in funzione della sua velocità e della sua accelerazione: rappresenta
dunque la legge oraria del moto.
OSSERVAZIONI
Ø
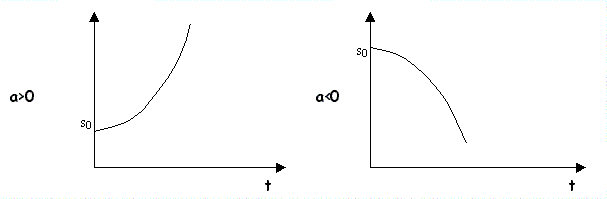
Se
rappresentiamo in un sistema di assi cartesiani la grandezza s in ordinata
(variabile dipendente) e la variabile t in ascissa (variabile indipendente), il
grafico che si ottiene sarà una parabola, con concavità rivolta verso l’alto
se a>0
(moto uniformemente decelerato), verso il basso se
a<0 (moto uniformemente
accelerato)
Ø
La pendenza
della retta tangente al grafico orario in ciascun istante di tempo t
rappresenta il modulo della velocità istantanea relativa all’istante
considerato.
Ø
Dal momento
che l’accelerazione istantanea coincide con l’accelerazione media calcolata
in qualunque intervallo di tempo
![]() , allora essa è data dalla pendenza della retta che rappresenta il grafico
(v,t).
, allora essa è data dalla pendenza della retta che rappresenta il grafico
(v,t).
LEGGI
DEL MOTO UNIFORMEMENTE VARIO
ESEMPI
SVOLTI MOTO UNIFORMEMENTE ACCELERATO
1)
Un’auto, su una pista rettilinea lunga 5 km, raggiunge in 8 s la
velocità di 95 km/h. Determinare lo spazio percorso nel tempo considerato.
Determina poi in quanto tempo raggiunge la velocità di 160 km/h, supponendo che
continui a muoversi sempre con la stessa accelerazione.
DATI
d
= 5 km = 5000 m
t
= 8 s
v0
= 0
v
= 95 km/h = 26,4 m/s
v2
= 160 km/h = 44,4 m/s
RISOLUZIONE
Scegliamo
un sistema di riferimento rettilineo, con il verso concorde al verso di moto
dell’auto e avente l’origine nel punto in cui l’auto inizia a muoversi.
La
legge della velocità dell’auto è:
![]()
Risolvendo
rispetto ad a, determiniamo con quale accelerazione si muove l’auto:
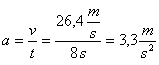
L’equazione
oraria dell’auto è:
![]()
Per
cui, sostituendo i dati a disposizione:
![]()
Per
determinare in quanto tempo raggiunge la velocità v2 = 44,4 m/s,
basta risolvere la legge delle velocità rispetto a t:
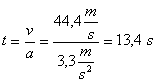
2)
Un oggetto parte da fermo e percorre di moto rettilineo uniformemente
accelerato 1,8 m in 3,0 secondi.
Qual
è l’accelerazione dell’oggetto?
DATI
s
= 1,8 m
t
= 3,0 s
RiSOLUZIONE
L’equazione
oraria del moto dell’oggetto sarà data da :
s
=
![]() essendo s0 = 0 e v0 = 0
essendo s0 = 0 e v0 = 0
da
cui si ricava che:
a
=
![]() e sostituendo i dati del problema, si ottiene:
e sostituendo i dati del problema, si ottiene:
a
=
![]() = 0,4 m/s2
= 0,4 m/s2