ACCELERAZIONE MEDIA

Consideriamo un punto materiale che si muove su una traiettoria qualsiasi.

L’accelerazione  media  del corpo è il rapporto tra l’intervallo tra due velocità, , assunte dal punto materiale in moto e l’intervallo tra i corrispondenti istanti di tempo :

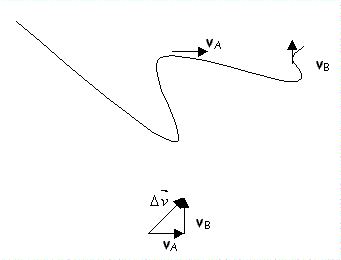
Dal punto di vista dimensionale l’accelerazione, essendo definita come il rapporto tra una velocità e un intervallo di tempo, è ricavabile da:

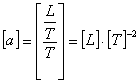
Essa, nel S.I., si misura in m/s².

Un’informazione importante deriva dalla pendenza del grafico definita come il rapporto tra  e , dove è l’incremento subito dalla variabile y in seguito all’incremento  della variabile indipendente x:

pendenza =

In un grafico v-t la pendenza della tangente al grafico indica l’accelerazione media del corpo nell’intervallo temporale considerato. Nel caso rappresentato nella figura (a) il corpo è dotato di un’accelerazione media positiva, nel caso (b) negativa, nel caso (c) nulla.

ACCELERAZIONE ISTANTANEA

Supponiamo, adesso, di voler determinare l’accelerazione assunta da un punto materiale in un ben determinato istante. Dal momento che, come già detto, è impossibile dal punto di vista operativo parlare di “istante di tempo”, l’accelerazione istantanea è definita come l’accelerazione media del punto materiale relativa ad un intervallo di tempo piccolissimo, al limite tendente a zero. Dal punto di vista formale:

In questo caso la pendenza della retta coincide con la tangente in quel punto e pertanto indica l’accelerazione istantanea nell’istante considerato.

ESEMPI SVOLTI

1)      Un ciclista pedala alla velocità di 36 km/h e, durante gli ultimi 5 secondi dello sprint finale, aumenta la sua velocità con una accelerazione media di 0,2 m/s². Calcola la velocità con cui il corridore taglia il traguardo.

DATI

              v_i = 36 km/h

               = 5s

              a = 0,2 m/s²

RISOLUZIONE

Dalla formula inversa dell’accelerazione ricaviamo la variazione di velocità:

     =a · = 1 m/s

    Trasformiamo nel S.I.:

          36 km/h = 10 m/s

    La velocità con cui il corridore taglia il traguardo sarà pertanto:

           v_f =  + v_i = (1+10) m/s = 11 m/s = 39,6 km/h

2)    Una moto viaggia alla velocità di 70 km/h. Premendo il pedale dell’acceleratore la velocità aumenta con accelerazione costante di 2 m/s² fino a 142 km/h. Calcola il tempo in cui è avvenuta tale variazione di velocità.

DATI

v_i   = 70 km/h

v_f = 142 km/h

a = 2 m/s²

RISOLUZIONE

     La variazione di velocità subita dalla moto è :

     = (142-70) km/h = 72km/h = 20 m/s

Dalla formula inversa dell’accelerazione ricaviamo il tempo:

t= =10 s