![]()
|
Io li credetti; e ciò che’n sua fede era, (Par. VI 19-21) |
Come si arguisce da questi versi, nella Divina Commedia è possibile trovare numerosi riferimenti alla disciplina che è alla base di ogni branca della Matematica e della Fisica: la Logica. Naturalmente con questo termine non si vuole indicare la Logica Matematica fondata intorno alla metà del XIX secolo da Georges Boole (1815-1864), ma alla Logica di Aristotele (384-322 a.C.), il filosofo greco che fu precettore di Alessandro Magno e che Dante riconosce come massima espressione del pensiero umano, dal « Maestro di color che sanno » (Inferno IV, 131). Il filosofo di Stagira fondò la Logica negli scritti cui i posteri daranno il titolo di "Organon", cioè di "strumento" propedeutico ad ogni studio scientifico.
L'Organon comprende:
le Categorie, che trattano della classificazione di tutto ciò che vi è;
il De Interpretatione, riflessioni sul linguaggio e sul concetto di necessità;
gli Analitici Primi, ovvero la sillogistica;
gli Analitici Secondi, comprendenti problemi di filosofia della logica;
i Topici, prescrizioni su come argomentare durante le dispute;
le Confutazioni Sofistiche, discussioni di argomentazioni fallaci.
Il termine "Logica" comparirà solo più tardi, nella trattazione stoica, ma Aristotele ha il merito di aver inaugurato lo studio consapevole ed approfondito del ragionamento corretto. Tuttavia prima di lui, di quella che oggi chiamiamo Logica , faceva già parte la dimostrazione per assurdo, ideata dai pitagorici, i quali se ne erano già serviti ad esempio per dimostrare che il rapporto tra la diagonale e il lato di un quadrato non è un numero razionale. La dimostrazione per assurdo si prefigge di dimostrare la proposizione A negandola e dimostrando che non A conduce ad una contraddizione: per la prima volta era emersa una struttura di tipo logico. Aristotele però va in là, arrivando al concetto di sillogismo, attraverso l'impostazione della proposizione nella coppia soggetto-predicato (S-P).
L’Organon aristotelico vuole stabilire le regole del ragionamento corretto, in modo che, partendo da alcune verità e seguendo delle regole precise, si possa automaticamente affermare quale proposizione è inconfutabilmente vera e quale è falsa. La verità dipende dalle premesse e non incide sulla validità del ragionamento. Per questo la logica aristotelica verrà poi definita formale, in quanto non intacca il contenuto e nemmeno ne dipende; verrà detta anche simbolica, perchè si avvale di simboli per indicare i termini di cui si compone il suo linguaggio, proprio per sottolinearne l’indipendenza dai contenuti. La Logica di Aristotele parte da queste tre leggi fondamentali:
1) Principio di identità: ogni proposizione è determinata ed equivalente a se stessa (A=A è sempre vera).
2) Principio di non contraddizione: una proposizione non può essere contemporaneamente vera e falsa.
3) Principio del terzo escluso: ogni proposizione può essere solo o vera o falsa, senza altre possibilità (cioè non vi è qualcosa di intermedio fra la verità e la falsità). In Metaphysica, B 2 Aristotele afferma:
« È necessario in ogni caso affermare o negare, ed è impossibile simultaneamente essere e non essere ».
A partire da queste basi, Aristotele fonda il sillogismo categorico (cioè le cui proposizioni esprimono l'appartenenza di un predicato ad un soggetto), essenza di ogni ragionamento. In pratica, il sillogismo (dal greco "ragionamento concatenato") è costituito da tre proposizioni: premessa maggiore, premessa seconda e conclusione. Ogni proposizione categorica è caratterizzata quantitativamente (è universale o particolare) e qualitativamente (è affermativa o negativa). Sono quindi possibili quattro forme che una proposizione categorica può assumere:
universale affermativa (« Tutti gli S sono P »), l’estensione del soggetto è totalmente inclusa nell’estensione del predicato;
particolare affermativa (« Qualche S è P »), nel caso in cui l’estensione del soggetto sia parzialmente inclusa nell’estensione del predicato;
universale negativa (« Nessun S è P »), se l’estensione del soggetto è totalmente esclusa dall’estensione del predicato;
particolare negativa («Qualche S non è P»), se l’estensione del soggetto non è totalmente inclusa nell’estensione del predicato (esiste almeno un individuo che cade sotto S ma non sotto P).
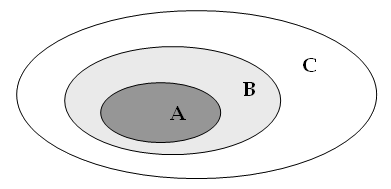
Si hanno poi quattro possibilità, le cosiddette quattro figure del sillogismo, in base alla posizione che assumono i termini nella proposizione, cioè a quale costituisce il soggetto e quale il predicato delle premesse. In tutto dunque si ottengono 256 schemi, detti "modi del sillogismo": per ogni figura abbiamo 4 possibilità per la premessa maggiore, 4 per la seconda e 4 per la conclusione, quindi 64 modi (4 x 4 x 4) in ogni figura; moltiplicandole per le quattro figure del sillogismo, si ottengono 256 modi possibili. Non tutti saranno però forme di ragionamento corretto: sono ritenuti validi solo 19. Ad esempio, nella prima figura sono possibili quattro modi, delle quali sono possibili altrettante rappresentazioni insiemistiche usando l'operazione di inclusione di un insieme in un altro:
|
Tutti
i B sono C |
Tutti gli ateniesi
sono uomini |
|
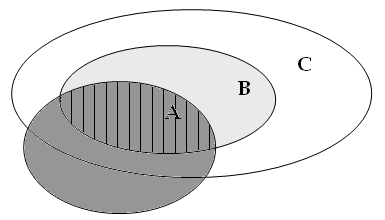
Tutti
i B sono C |
Tutti i primati sono
mammiferi |
|
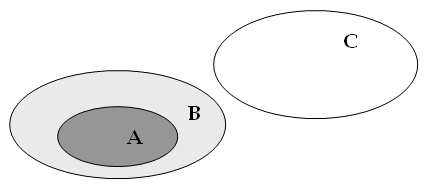
Nessun
B è C |
Nessun uomo è
immortale |
|
Tutti
i B sono C |
Tutti i primati sono
mammiferi |
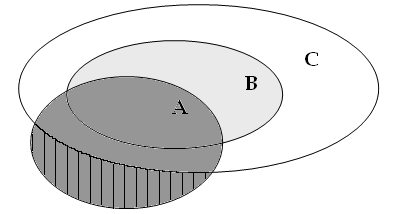
Nella manualistica medievale furono poi introdotti vari meccanismi mnemonici per ricordare i 19 sillogismi validi, ma non è il caso in questa sede di insistere su di essi. Teniamo piuttosto a mente il terzo dei modi sopra riportati, perchè tra poco vedremo come il « ghibellin fuggiasco » ne farà uso.
![]()
Di tutto questo abbiamo discusso così ampiamente perchè è da Aristotele che derivano le basi di tutti gli studi logici del Medioevo, incluso il pensiero di Tommaso d'Aquino (1225-1274), il "Doctor Angelicus" che Dante incontra nel X Canto del Paradiso. Nel suo "Trattatello in laude di Dante", Giovanni Boccaccio accenna ad un viaggio di Dante a Parigi, in cui avrebbe appreso le basi della logica aristotelica. Di questo viaggio non esistono prove storiche, ma l'aristotelismo contava esponenti di gran spicco anche nella Facoltà di Bologna che Dante sicuramente frequentò. Anzi, gli studi di logica modale a Bologna non andarono incontro alle condanne che subirono invece a Parigi, dal momento che Bologna mancava della facoltà di teologia, e quella di giurisprudenza era protetta dall’imperatore. D'altra parte nessuno contesterebbe la formazione prettamente logica del filosofare dantesco, visto che nel Medioevo alla base di ogni insegnamento vi erano le tre discipline del Trivio: Grammatica, Retorica e Dialettica, e quest'ultima in particolare comprende gran parte degli studi di logica.
Nel passo del Paradiso da cui la nostra investigazione ha preso avvio, l’imperatore Giustiniano (482-565) si appresta a ripercorrere la storia dell’Impero Romano, dall'eroe virgiliano Pallante (VI, 36) fino a Carlo Magno (VI, 96), ma prima accenna alla propria vicenda terrena, e in particolare al fatto (non confermato dagli storici moderni) che egli avrebbe inizialmente aderito all’eresia monofisita, e si sarebbe in seguito convertito al cattolicesimo in seguito all'incontro con Papa Agapito (535-536), che si era recato a Costantinopoli per mediare la pace tra Giustiniano e Teodato, re degli Ostrogoti. Dante sottolinea l'irrazionalità dell'ingenua adesione al monofisismo, basata solo su un puro atto di fede:
«
Una natura in Cristo esser, non piùe,
credea, e di tal fede era contento » (VI, 14-15)
Inizialmente anche la conversione al cattolicesimo è basata sull'abilità di predicazione da parte del Papa, e quindi sulla fede nelle sue parole:
«
'l benedetto Agapito, che fue
sommo pastore, a la fede sincera
mi dirizzò con le parole sue.
Io li credetti... » (VI, 16-19)
In seguito l'adesione fideistica al credo niceno assume i connotati di verità dimostrabile logicamente, tanto che l'imperatore lo vede con la stessa chiarezza ed evidenza con cui Dante comprende che, tra due proposizioni che si contraddicono, una è necessariamente vera e l'altra falsa:
«
...e ciò che 'n sua fede era,
vegg'io or chiaro sì, come tu vedi
ogni contraddizion e falsa e vera. » (VI, 19-21)
Evidentemente qui Dante fa riferimento al suddetto principio del terzo escluso, che come abbiamo visto è uno dei postulati della logica aristotelica. In tal modo Giustiniano fa riferimento diretto al proprio cammino di fede: dopo aver conosciuto due teorie opposte sulla natura di Cristo, e averne seguita una per fede, ora è in grado di vedere in modo logicamente chiaro che la prima era falsa, e la seconda vera. Così infatti scrive il Benvenuto, commentatore dantesco del XIV secolo:
« Quicquid tenebam de fidem per solam credulitatem, nunc video per certitudinem ita clare, sicut tu cognoscis aliquam rem vel conclusionem in tua scientia » (Ciò in cui credevo solo per fede, ora lo vedo con certezza e così chiaramente, come tu intendi questo o quell'oggetto o conclusione della tua scienza)
Vale la pena di riportare anche la teoria di Bruno d'Amore, docente di Didattica della matematica alle Università di Bologna e Bolzano, che preferisce leggere in questi versi un riferimento al cosiddetto "Metateorema dello Pseudo-Scoto", enunciato nelle "Summulae logicales" di Pietro Ispano, Papa dal 15 settembre 1276 al 20 maggio 1277 con il nome di Giovanni XXI (tra l'altro fu l'unico pontefice portoghese della storia), che Dante conosceva e cita nel Paradiso (XII,135: « lo qual giù luce in dodici libelli »). Secondo tale teorema, a partire da una contraddizione si può dimostrare qualunque cosa, sia il falso che il vero. D'Amore afferma di preferire questa seconda interpretazione perché più coerente con il senso dell’intero passo: mentre il principio del terzo escluso, in quanto postulato, ha ancora teoricamente qualcosa del puro atto di fede, quello dello Pseudo-Scoto è un vero e proprio Teorema, e quindi più vicino alla nuova dimensione dimostrativa e razionale in cui Giustiniano vede la fede cattolica.
L'ipotesi non è priva di fascino. Ma questo non è certo l'unico passo in cui Dante dimostra di aver appreso a perfezione le strutture della Logica aristotelica, al punto che, nella dimensione ultraterrena del suo Oltremondo, le strutture di pensiero della scienza vengono estese a qualunque tipo di realtà, anche nell'ambito della filosofia e della teologia. Ad esempio, nel Cielo del Sole, presentando a Dante l'anima di Sigieri di Brabante, il maggior pensatore della corrente averroistica nel XIII secolo, Tommaso d'Aquino dice di lui:
«
Essa è la luce etterna di Sigieri,
che, leggendo nel Vico de li Strami,
silogizzò invidïosi veri. » (Par. X, 136-138)
Questi difficili versi significano che Sigieri, insegnando ("leggere" era verbo usato a quel tempo per indicare le lezioni universitarie) nella Rue du Fouarre, la "Via della Paglia" a Parigi, dove sorgevano le scuole di filosofia, "sillogizzò", cioè sostenne con rigorose argomentazione dialettiche dei concetti filosofici che gli avrebbero portato la fama di eretico, facendolo perseguitare da parte del clero parigino. Infatti Sigieri morì ad Orvieto nel 1283, assassinato dal proprio stesso segretario. Tra le idee "eretiche" da lui sostenute vi erano la negazione della creazione dal nulla, dell'immortalità dell'anima e del libero arbitrio, anche se egli sostenne sempre che come credente in Gesù Cristo poteva rinnegare quelle teorie che sosteneva sul piano filosofico (e per questo l'Alighieri lo pone nel Paradiso). Come si vede, qui Dante usa il verbo "fare sillogismi" come sinonimo stesso di "pensare"! E all'inizio del canto seguente Dante ribadisce questo concetto con i seguenti, famosissimi versi:
«
O insensata cura de' mortali,
quanto son difettivi silogismi
quei che ti fanno in basso batter l'ali! » (Par. XI, 1-3)
L'apostrofe dantesca ha questo significato: o folle preoccupazione degli uomini, come sono falsi i ragionamenti che rivolgono gli animi degli uomini ai soli interessi terreni! Si ritrova qui l'eco di un passo di Persio:
« O curas hominum! O quantum est in rebus inane! » (Satira I, 1)
Non basta. Nel Cielo delle Stelle Fisse Dante è interrogato da San Pietro circa la Fede, e gli domanda da chi e come essa gli fu donata. Il Poeta replica:
«
La larga ploia
de lo Spirito Santo, ch'è diffusa
in su le vecchie e 'n su le nuove cuoia,
è sillogismo che la m'ha conchiusa
acutamente sì, che 'nverso d'ella
ogne dimostrazion mi pare ottusa. » (Par. XXIV, 91-96)
Vale a dire: l'ispirazione, che si effonde come pioggia copiosa ("larga ploia") nelle pagine ("cuoia", perchè fatte di pergamena) del Vecchio e del Nuovo Testamento, è un argomento così efficace e così convincente, che ogni altra dimostrazione al confronto mi pare poca cosa. Il concetto è ripreso da San Bonaventura di Bagnoregio ("In Hexaemeron I, 30), ma soprattutto ritorna il concetto di "sillogismo" aristotelico come sinonimo dell'atto di ragionare. Ora, voi vi chiederete: è possibile ritrovare in Dante non solo l'allusione al mettere insieme sillogismi, ma un vero e proprio sillogismo come quelli da noi esemplificati sopra? La risposta è sì, anche se ci stupirà. Infatti sembrerà assurdo, ma uno dei personaggi che più fa sfoggio di una logica inoppugnabile nel poema di Dante non è Virgilio, né Beatrice, bensì… un diavolo.
![]()

Dante e Virgilio nella bolgia dei consiglieri fraudolenti, visti da Gustave Dorè
Ci troviamo per la precisione nel XXVII Canto dell'Inferno (successivo a quello celeberrimo di Ulisse), e Dante incontra Guido da Montefeltro (1220-1296), « il più sagace e il più sottile uomo di guerra ch'al suo tempo fosse in Italia » (Villani, Cronica, VII, 80). Questo astuto uomo d'arme, per certi versi una sorta di secondo Ulisse:
«
Mentre ch'io forma fui d'ossa e di polpe
che la madre mi diè, l'opere mie
non furon leonine, ma di volpe.
Li accorgimenti e le coperte vie
io seppi tutte, e sì menai lor arte,
ch'al fine de la terra il suono uscie. » (XXVII, 73-78)
Insomma, secondo Guido stesso (abbastanza vanaglorioso, in verità) la fama di questa sua astuzia volpina si diffuse fino agli estremi confini della terra. Scomunicato in quanto capo dei ghibellini di Romagna, il furbacchione si riconciliò con la Chiesa nei suoi ultimi anni e si fece frate francescano:
«
Quando mi vidi giunto in quella parte
di mia etade ove ciascun dovrebbe
calar le vele e raccoglier le sarte,
ciò che pria mi piacea, allor m'increbbe,
e pentuto e confesso mi rendei;
ahi miser lasso! e giovato sarebbe. » (XVIII, 79- 84)
Guido nella vecchiaia decide di ammainare le vele e raccogliere le funi (una metafora assai comune, forse non casuale rimando "marittimo" all’Ulisse del canto precedente). Il peccato però è in agguato, e gli si manifesta sotto le spoglie dello stesso pontefice Bonifacio VIII ("Lo principe d'i novi Farisei"). Questi infatti lo convince a dargli l'ultimo consiglio fraudolento, in particolare come porre fine alla resistenza di Palestrina, roccaforte dei Colonna, che si erano ribellati al suo controllo, dietro la promessa dell’assoluzione:
«
E' poi ridisse: "Tuo cuor non sospetti;
finor t'assolvo, e tu m'insegna fare
sì come Penestrino in terra getti. » (XVIII,
100- 102)
Fra Guido ci casca e fornisce il suo cattivo consiglio: indurre i Colonna ad arrendersi dietro promessa della restituzione dei loro privilegi, per poi disattendere alla parola data. Alla sua morte, avvenuta non molto tempo dopo, Dante mette in scena una vera e propria "sacra rappresentazione" dal sapore medievale: spesso nelle piazze dei Comuni italiani venivano rappresentate delle dispute tra un diavolo e un santo, immancabilmente vinte da quest'ultimo. Ma nel nostro caso le cose vanno diversamente: ad aver la meglio è « un de’ neri cherubini », e per di più a rigor di logica!
« Francesco venne poi, com’io fu’ morto,
per me; ma un de’ neri cherubini
li disse: "Non portar: non mi far torto.
Venir se ne dee giù tra’ miei meschini
Perché diede il consiglio fraudolente,
dal quale in qua stato li sono a’ crini;
ch’assolver non si può chi non si pente,
né pentere e volere insieme puossi
per la contraddizion che nol consente!" » (XXVII, 112-120)
Questo grottesco bisticcio per il possesso dell’anima del poveretto è vinto dal demonio facendo ricorso ad un vero e proprio sillogismo di stampo aristotelico. Traducendolo in termini logici, esso suona più o meno così:
Ogni pentito
può essere assolto.
Nessun pentito è peccatore volontario.
Quindi Guido non può essere assolto.
Ovvero, con la notazione insiemistica moderna (U = l'insieme universo formato da tutti gli uomini; A = l'insieme degli assolti; P = l'insieme dei pentiti; V = l'insieme dei peccatori volontari):
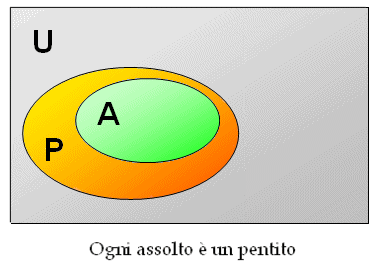
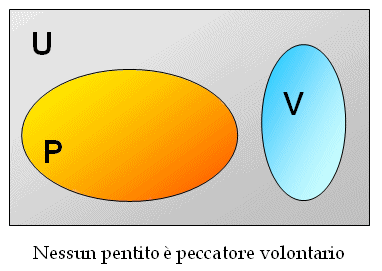
quindi:
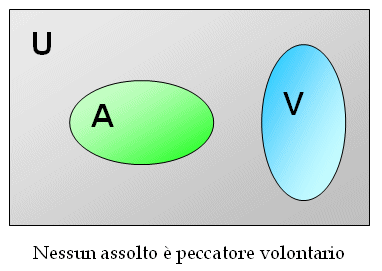
E questo è precisamente il terzo dei modi del sillogismo aristotelico che abbiamo preso in considerazione sopra! La conclusione è talmente inconfutabile sul piano razionale, che l'angelo caduto si permette persino di prendere in giro la sua vittima: chi lo avrebbe mai detto che anche i diavoli sono "loici" (logici), sanno cioè padroneggiare così bene la logica aristotelica, da mettere nel sacco anche colui che si era vantato di conoscere tutti « li accorgimenti e le coperte vie »?
«
Oh me dolente! Come mi riscossi
Quando mi prese dicendomi: "Forse
tu non pensavi ch’io loico fossi!" » (XXVII 121-123)
Questo breve eppur concitato passo ci dà un chiaro esempio di come la chiarezza dei ragionamenti, l'impostazione deduttiva di stampo aristotelico, la nitida struttura del pensiero, tutto ciò che insomma non potremmo definire con altro termine che logica, è innegabilmente presente in ogni aspetto della visione dantesca del mondo.
Un altro chiaro riferimento alla logica dei sillogismi lo troviamo nel Paradiso, messo in bocca nientemeno che al già citato San Tommaso d'Aquino:
...o se necesse
con contingente mai necesse fenno » (Par. XIII 98-99)
Così Bruno d'Amore nel suo lavoro commenta questi versi:
« Si tratta di un passaggio "tecnico" di logica modale: in un sillogismo una premessa necessaria e una contingente possono dare una conseguenza necessaria? Il problema, non banale, era già stato affrontato e negativamente risolto da Aristotele in Analitici primi I 16. Dunque, una questione erudita di logica tecnica che Dante mostra di conoscere e alla quale fa volentieri ricorso (tutta l'argomentazione di questo brano è logica, dato che si sta dibattendo una questione teologica ed è risaputo che Tommaso d'Aquino era ben noto per le sue argomentazioni teologiche con strumenti di sofisticata logica). »
Una picccola curiosità per chiudere. Avete mai sentito parlare del "Comma 22"? Si tratta di un neologismo moderno che indica una situazione paradossale, o meglio ancora una procedura assurda. Questa espressione trae origine dal "paradosso del Comma 22" contenuto nel romanzo "Tranello 22" (1961) dello scrittore americano Joseph Heller (1923-1999). Esso narra le avventure di un gruppo di aviatori statunitensi in Italia durante la seconda guerra mondiale, i quali consultano i regolamenti militari vigenti e si rendono conto dell'esistenza in essi di due articoli di invenzione letteraria, di fatto contraddittori tra loro: l'Articolo 12, Comma 1 per il quale l'unico motivo valido per chiedere il congedo dal fronte è la pazzia; l'Articolo 12, Comma 22 che dichiara che chiunque chiede il congedo dal fronte non è pazzo. Si tratta di una rivisitazione del più noto paradosso di Philip Jourdain (1879-1919), espresso come segue: « la frase seguente è falsa. La frase precedente è vera ». E anche questo a Dante era già ben noto!
Ma questo non è certo l'unico passo del Poema in cui è possibile rintracciare le conoscenze matematiche dell'uomo Dante, e quindi dell'intero Medioevo, di cui l'Alighieri è la sintesi somma. Per sincerarvene, cliccate qui e seguitemi nel nostro viaggio attraverso il testo in terzine.