Babele, nel paese di Sennaar

Come si arguisce dalla citazione qui sopra, in questo capitolo parleremo della Torre di Babele, la mitologica costruzione che i discendenti di Noè, poche generazioni dopo il diluvio, eressero come sfida a Dio, perchè nessun diluvio potesse più abbatterla. Il racconto contenuto nel capitolo 11 della Genesi lo conosciamo tutti; è di tradizione Jahvista (risale dunque al Regno di Davide e Salomone) e intende spiegare la molteplicità delle lingue sulla Terra come conseguenza del castigo di una colpa collettiva che, come quella di Adamo ed Eva, consiste in un peccato di orgoglio dissennato. La Genesi non specifica esattamente chi ebbe l'idea di costruirla, come se la responsabilità cadesse su tutti gli uomini dell'epoca, ma siccome nel capitolo precedente ha presentato in questi termini il personaggio di Nimrod, nipote di Cam:

« L'inizio del suo regno fu Babele, Uruch, Accad e Calne, nel paese di Sennaar... » (Gen 10, 10)

fu facile attribuire al mitologico sovrano « valente nella caccia » la responsabilità della costruzione della Torre, dato che il suo regno era inizialmente centrato attorno a Babele (cioè a Babilonia). Dante Alighieri crede a questa attribuzione, tanto da ritrarre in maniera quasi scultorea, nella cornice del Purgatorio dedicata ai Superbi, il mitico sovrano intento a rimirare i propri sudditi e il proprio lavoro, destinato a rimanere in eterno simbolo di incompiutezza e di superbia punita:

« Vedea Nembròt a piè del gran lavoro
quasi smarrito, e riguardar le genti
che 'n Sennaàr con lui superbi fuoro. » (Purg. XII, 34-36)

Della nostra Torre parla anche il Libro dei Giubilei, un testo apocrifo dell'Antico Testamento scritto nel II secolo a.C. da un pio giudeo che rivisitò la storia di Israele dividendola in Giubilei, cioè in periodi di 49 anni. Così esso descrive la costruzione e la fine della Torre:

« E la costruirono per quaranta anni e, per tre anni, stettero a costruire mattoni ognuno della larghezza di tre, della lunghezza di dieci e dell'altezza di tre. Ed essa si innalzò per 5433 cubiti, due spanne e quindici me'eraf. E ci disse il Signore, nostro Dio: "Ecco, erano un sol popolo. Hanno cominciato a lavorare ed ora nessuno di loro la finirà. Venite! Scendiamo e confondiamo le loro lingue: l'uno non comprenderà la parola dell'altro e siano dispersi fra i paesi e i popoli e non vi sia più, così, fra di loro, un solo modo di intendersi, fino al giorno del giudizio". E il Signore discese, e noi con Lui, per vedere la città e la torre che i figli degli uomini avevano costruito. Ed Egli confuse tutte le parole dei loro linguaggi e l'uno non intese più le parole dell'altro e interruppero, allora, la costruzione della città e della torre. E, perciò, tutta la terra di Sennar fu chiamata Babele poiché colà il Signore disgregò tutti i linguaggi dei figli degli uomini e di là furono dispersi in tutti i loro paesi, ognuno secondo il proprio linguaggio e la propria nazione. E il Signore mandò un gran vento sulla torre e la abbatté a terra ed ecco, quella torre è fra la terra di Assur e di Babilonia, nella terra di Sennaar, e si chiama Deqat. » (Giubilei X, 18-26)

Sui dettagli di questo fantasioso racconto, che aggiunge molti particolari alla Genesi, soddisfacendo la fantasia dei lettori molto più degli scarni versetti biblici, torneremo tra poco. Per ora vale la pena di spendere due parole sull'origine di questo episodio, divenuto uno dei più noti soggetti della Storia dell'Arte, come dimostra un celebre dipinto del 1563 di Pieter Bruegel il Vecchio (1525-1569). Oggi si pensa che la vicenda della Torre, così come ci è pervenuta, si sia originata durante la cattività babilonese (fra il 586 e il 539 a.C.): una volta portati in esilio nella grande Babilonia, i Giudei vi trovarono la grande ziggurat Etemenanki, la tradizionale torre a gradoni mesopotamica costruita probabilmente all'epoca di Hammurabi (1792-1750 a.C.) e ampliata varie volte fino all'epoca di Alessandro Magno. In particolare gli Ebrei trovarono incompiuto il rifacimento del re caldeo Nabopolassar (625-604 a.C.) e di suo figlio Nabucodonosor II (604-562 a.C.), il distruttore del Tempio di Gerusalemme. La ziggurat Etemenanki (in lingua sumerica "pietra angolare del cielo e della terra") era dedicata al dio Marduk, e all'epoca di Nabucodonosor II era alta 30 cubiti, cioè circa 15 metri, come si deduce dalle iscrizioni del tempo. Ne parla con ammirazione anche Erodoto di Alicarnasso (484-430 a.C.), secondo il quale (Storie I, 181), nel momento di massimo splendore, l'Etemenanki aveva la base quadrata di 91,5 metri di lato, misura verificata archeologicamente, e si pensa che avesse anche la medesima altezza, il che ne faceva il terzo edificio più alto del mondo antico dopo le Piramidi di Cheope e di Chefren.

A Babilonia, inoltre, gli Ebrei sentivano parlare tutte le lingue del mondo, giacché essa era capitale di un impero immenso, esteso dai deserti dell'Arabia fino ai monti dell'Armenia, e delegazioni di ogni popolo sottomesso vi si recavano per omaggiare il sovrano. Babilonia in lingua accadica significa "Porta di Dio" (Bab-El), ma gli intellettuali d'Israele associarono il nome della città al termine ebraico "balal", cioè "confusione". Collegando il caos delle lingue alla mole imponente della ziggurat ancora incompiuta, nacque la leggenda della torre costruita dagli antichi per scalare il Cielo, simbolo dell'arroganza umana punita con la confusione delle lingue e con la dispersione dei suoi costruttori su tutta la faccia della Terra.

Molto più tardi. il Targùm Yerushalmi (traduzione e parafrasi in ebraico dell'intera Torah con alcune digressioni retoriche, poetiche e mistiche, composta al più tardi nella seconda metà del VII secolo) commenta il brano della Torre di Babele affermando che in cima ad essa doveva esserci una statua d’uomo con una spada in mano, e quindi un idolo. L'autore di questo Targum intravede dunque chiaramente nell'opera dei costruttori un atto di idolatria e di ribellione contro Dio. Si noti che questo commento cancella di colpo tutte le interpretazioni rabbiniche che vedono in Babele un tentativo di giungere fino al Cielo, dimora del Signore, o di offrire protezione contro un eventuale secondo Diluvio Universale, per tornare a quello che era il vero significato originale della ziggurat mesopotamica, e cioè una montagna artificiale sopra la quale era edificato il tempio di una divinità (con il suo idolo, di solito una scultura imponente), analogamente a quanto si faceva in età protostorica, quando gli déi erano venerati in cima ad una montagna per avvicinarsi il più possibile alla sua dimora celeste!

Dato poi che questo è un ipertesto scientifico, tra le interpretazioni più fantasiose della Torre di Babele è degna di menzione quella di Rabbeinu Bachya, studioso vissuto a Saragozza nell'XI secolo, il quale suggerisce che forse quei nostri lontani antenati stavano fabbricando... il primo parafulmine! Infatti essi sapevano che Dio aveva promesso di non mandare un altro diluvio (Gen 9, 14-15), e temevano che Egli avrebbe invece punito i peccatori del futuro con il fuoco dei fulmini. Perciò speravano che la torre avrebbe deviato qualsiasi tempesta elettromagnetica mandata da Dio! Si noti peraltro che Rabbeinu Bachya era vissuto sette secoli prima di Benjamin Franklin, l'inventore del parafulmine!

Infine, la Torre di Babele ha ispirato nel 1976 anche il compositore Edoardo Bennato: « Non vi fermate, / dovete costruire la vostra torre, / la Torre di Babele: / sempre più grande, / sempre più alta e bella / ...Siete o non siete i padroni della terra? » Molto significativa è la copertina del 45 giri, visibile qui sotto, delle Edizioni Musicali Cinquantacinque, nel quale la biblica Torre è identificata con l'intera umanità di tutti i tempi, con le sue armi e con la sue conquiste tecnologiche, che culminano nel "Saturno V" al posto del Tempio di Marduk:

Detto questo, possiamo porci il quesito che dà il titolo al capitolo presente: quanto era alta la Torre di Babele? La Genesi, come si è visto, non fornisce cifre, a differenza di quanto fa per l'Arca di Noè, lasciando alla fantasia dei fedeli la possibilità di immaginare un edificio di proporzioni strabilianti. Il famoso poeta romanesco Giuseppe Gioacchino Belli (1791-1863) infatti così descrive il patatrac che accade ai costruttori della « Torre di Babbelle » in seguito all'intervento divino, nel sonetto "Er Monno muratore" del 17 febbraio 1833:

« Già ssò ar par de la croce de San Pietro,
quanno, ch’edè? Je s’imbroja er filello,
e invece d’annà avanti vanno addietro... »

La cupola di San Pietro è alta 133,3 metri, dunque molto più della massima altezza supposta della Ziggurat di Babilonia, che fece da modello per la mitologica costruzione. Ma si tratta solo della fantasia di un poeta ottocentesco, che misurava tutto il mondo sulle proporzioni della sua Roma, e dunque come prototipo di edificio altissimo non poteva che prendere il Cupolone. Il Libro dei Giubilei, come si è letto sopra, parlava invece di « 5433 cubiti, due spanne e quindici me'eraf ». Come si è visto, un cubito biblico misurava 44,45 centimetri, una spanna 22,46 centimetri; sul me'eraf non abbiamo informazioni; la misura della Torre secondo l'autore dei Giubilei sarebbe dunque almeno pari a 5433 x 0,4445 + 2 x 0,2246 = 2415,42 metri. Una misura decisamente iperbolica, se si pensa che il più alto grattacielo mai costruito dall'uomo, il Burj Khalifa di Dubai, negli Emirati Arabi Uniti, raggiunge "appena" gli 829,8 metri, e fu inaugurato solo nel 2010. La più alta struttura artificiale costruita nell'antichità, la Piramide di Cheope, misurava in origine 146,6 metri (oggi la punta è scomparsa e si è ridotta a 138,8 metri), e dunque la Torre di Babele sarebbe stata sedici volte e mezza più alta! Quando dovrebbe essere stata vasta, dunque, la sua base? Davvero solo l'intera umanità riunita avrebbe potuto edificare un simile colosso. Naturalmente si tratta di una misura altrettanto fantasiosa di quella cui alludeva il Belli, tale da giustificare il modo di dire "dimensioni bibliche"!

Nulla però è neppure lontanamente paragonabile ai colossali obelischi di Egira, nell'omonimo romanzo del 1973 del grande autore di fantascienza Greg Bear (1951-). Egira è un mondo più grande della Terra, sulla superficie del quale sorgono imponenti obelischi di pietra alti mille chilometri e con un chilometro quadrato di base, piantati dai cosiddetti "Primogeniti" per tramandare ai "Secondogeniti" le loro conoscenze, la loro storia e la loro religione. In basso sono incise le conoscenze più semplici, mentre quelle più avanzate, tipiche di una società tecnologica dedita ai viaggi spaziali, sarebbero incise nella parte superiore, che nessuno è mai riuscito a leggere (con le mongolfiere, gli abitanti di Egira non sono riusciti a salire più di qualche chilometro. Questi obelischi sfiorano veramente il cielo, e questo li accomuna alla Torre di Babele; come la Torre, inoltre, anch'essi ad un certo punto crollano, causando cataclismi devastanti, ma permettendo agli abitanti di Egira di leggere tutte le iscrizioni su di essi: in un certo senso anch'essi aumentano la conoscenza umana, così come la fine della Torre di Nimrod segnò il nascere di tutte le lingue della Terra!

« Gli Obelischi erano un enigma del quale ben poco si era risolto nella storia dei Secondogeniti. Erano alti circa mille chilometri , e i quattro lati di un chilometro ognuno formavano sempre un quadrato perfetto. Durante il giorno, scomparivano nel blu infinito, e di notte riflettevano fiocamente la luce degli uccelli di fuoco, stagliandosi contro il cielo a perdita d'occhio. Sulle loro pareti erano scolpite intere civiltà; storia, filosofia, letteratura e descrizioni della Terra, che era il pianeta dei Primogeniti. [...] Più in alto si leggeva, più si andava avanti nel tempo, e più diventava sofisticata la tecnologia. A Ibis, i lettori erano arrivati fino a dieci chilometri di altezza usando palloni aerostatici. "Da ognuno sceglierete il sapore della vostra nascita", diceva il primo testo di ogni Obelisco, "il tempo del vostro tempo, le parole che pronuncerete e le cose che adorate. Tutto il resto sarà come il nulla per voi". » ("Egira", cap. 5, trad. di Marco Pinna)

In un certo senso, gli obelischi di Egira, dall'alto della loro mole straordinaria, realizzano il sogno degli autori della Genesi e del Libro dei Giubilei. Tuttavia, chiediamoci: è davvero possibile realizzare un obelisco di pietra alto mille chilometri, anche da parte di una civiltà così avanzata da sembrare quasi onnipotente? Per rispondere a questa domanda, dobbiamo calcolare la pressione esercitata alla base da un simile colosso. Com'è noto, la pressione è pari al rapporto tra la forza premente perpendicolare alla superficie e la superficie medesima. Se appoggio un mattone su una superficie orizzontale, la pressione è pari al rapporto tra la forza premente, cioè il peso del mattone, ottenuto moltiplicando la sua massa m per la sua accelerazione di gravità g, per l'area A della faccia del mattone appoggiata al suolo:

Questo semplice calcolo può essere eseguito per una torre a forma di parallelepipedo, con area di base A prefissata e di altezza H anch'essa prefissata, se però la torre non è troppo alta, in modo che l'accelerazione di gravità g si possa ritenere costante in ogni punto del suo volume. Il volume della torre è pari ad A H, e detta ρ la densità della torre, la sua massa è pari a m = ρ A H. La pressione P sulla sua base è perciò data da:

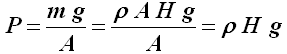
Consideriamo ad esempio ognuna delle due Torri Gemelle di New York distrutte nell'attentato terroristico dell'11 settembre 2001, e nella quale i terroristi islamici vedevano proprio una moderna Torre di Babele che incarnava l'arroganza plutocratica degli Stati Uniti d'America. Ciascuna torre era alta H = 415 metri ed aveva una base A = ( 63,4 m )² = 4019,56 m², e si stima che la sua massa fosse di 500.000 tonnellate, da cui si ricava che la pressione alla sua base era pari a 5 x 10⁸ kg x 9,8 m s^–2 / 4019,56 m² = 1,2 x 10⁶ Pa, cioè 12 atmosfere: una pressione 12 volte maggiore di quella atmosferica al livello del mare, ma sopportabile dal suolo dell'isola di Manhattan, e soprattutto dai primi piani che devono reggere tutti gli altri.

Il calcolo però non è così immediato se la torre diventa davvero altissima, come i mitologici obelischi di "Egira", poiché mano a mano che si sale lungo la torre, se la sua altezza è comparabile con il raggio terrestre, cambia anche la forza di gravità che la Terra esercita sui piani più alti. Si consideri dunque una sezione sottile delle torre, perpendicolare alla sua altezza, di spessore dx e posta alla quota x rispetto al suolo (la ho evidenziata in giallo nella figura sottostante):

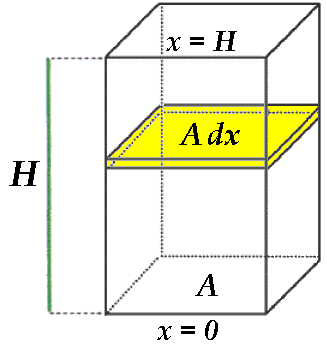
Il volume di tale sezione è A dx; detta ρ la densità della torre, la massa della sezione è dm = ρ A dx. Per questo calcolo adopereremo la legge di Newton, che potete trovare in questa pagina del mio ipertesto "La Mela di Newton". Siccome sappiamo (fu determinato rigorosamente da Newton) che la massa M_T della Terra può essere considerata come concentrata nel suo centro, se R è il raggio terrestre per la suddetta legge si ha:

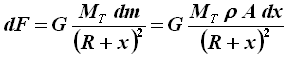
Per ottenere la forza complessiva esercitata dalla gravità sulla torre occorre integrare per x che va da 0 (la sua base) ad H (la sua sommità), ottenendo:

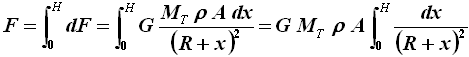
Risolviamo l'integrale:

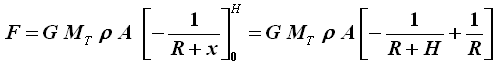
Con semplici calcoli si ottiene:

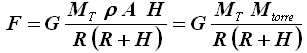
Infatti A H è il volume della torre, e ρ A H è la sua massa. Si osservi che quest'ultima si può scrivere:

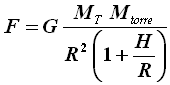
Allora, se H <<R, il rapporto H/R è trascurabile rispetto ad 1 e la precedente diventa F = G M_T M_torre / R², che è la formula di Newton valida per una massa puntiforme. In tal caso, infatti, la dimensione della torre è trascurabile rispetto al raggio terrestre, ed essa si comporta come tutti gli altri corpi di questo mondo. Ciò ci rassicura circa l'esattezza dei nostri calcoli.

A questo punto, possiamo determinare la pressione P alla base della nostra torre, che è pari al rapporto tra forza F e superficie A. Si ottiene così:

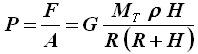
Consideriamo dunque uno dei tremendi obelischi di Egira, per i quali H = 1000 km = 10⁶ m. Supponiamo che fossero fatti di granito e pieni all'interno; la densità ρ del granito vale all'incirca 2750 kg/m³. Conoscendo G = 6,67 x 10^–11 N m²/kg², M_T = 6 x 10²⁴ kg e R = 6370 km = 6,37 x 10⁶ m, sostituendo i dati nella formula precedente si ottiene P = 2,34 x 10¹⁰ Pa = 2,3 x 10⁵ atmosfere. Si tratta della pressione che si riscontra all'interno della Terra a circa 1000 km di profondità, ed essa è tale da cambiare completamente la struttura della materia, sbriciolando letteralmente la base della torre e facendola collassare su se stessa. Conclusione: se è vero che l'altezza dell'atmosfera terrestre si può ritenere dell'ordine dei 1000 km, e per "toccare il cielo" (cioè lo spazio) occorre salire fino a questa quota straordinaria, pari a quella degli obelischi di Greg Bear, ebbene, occorre arrendersi all'evidenza dei nostri calcoli: nessun popolo, neppure i famosi Giganti dei tempi antichi, potrà mai cristallizzare la propria superbia in una torre di Babele così alta.

La torre Eiffel vista dal basso (da questo sito)

Tutto questo però nell'ipotesi che la torre di Babele avesse la forma di parallelepipedo. Ma noi sappiamo che non era così: l'autore del racconto del capitolo 11 della Genesi ha infatti presente la grande ziggurat di Babilonia, l'Etemenanki, che si stringeva mano a mano che si inerpicava verso l'alto. Tali sono anche le piramidi egiziane e le piramidi a gradoni Maya e azteche, oltre alle innumerevoli strutture analoghe scoperte in ogni parte del mondo. Ma non c'è bisogno di invocare Atlantide per spiegare la fortuna di questa modalità architettonica: infatti chiunque voglia costruire un edificio molto elevato con materiale povero, è portato a restringerlo verso l'alto per conferirgli maggiore stabilità. Allora poniamoci il problema contrario: quale forma deve avere la torre, in modo da raggiungere la massima altezza compatibile con la resistenza dei materiali a disposizione? Sorprendentemente, per rispondere a questa domanda conviene riferirci ad una delle più famose torri elevate nel nostro evo moderno: la Torre Eiffel, costruita in 2 anni, 2 mesi e 5 giorni di lavoro tra il 1887 al 1889, per l'Esposizione Universale del 1889, che si tenne a Parigi per celebrare il centenario della Rivoluzione Francese. Essa trae il nome dall'ingegnere Gustave Eiffel (1832-1923), che costruì anche la struttura interna della Statua della Libertà di New York. Alta 324 metri, pesa circa 8.000 tonnellate e può resistere a venti fino a 800 km/h. Oggi la torre è visitata ogni anno da almeno cinque milioni e mezzo di turisti, e rappresenta sicuramente una delle meraviglie del mondo moderno. Ma perché Eiffel diede alla sua opera più famosa proprio quella forma? Proviamo a fare insieme qualche calcolo.

Sia ρ è la densità del ferro. Stavolta l'area della sezione della torre non è costante, ma dipende dalla quota, pur rimanendo sempre quadrata; sia dunque A(x) l'area della sezione alla quota generica x. Ovviamente la torre Eiffel, rispetto agli obelischi di Bear, ha il vantaggio di avere una struttura cava all'interno, ma noi useremo lo stesso procedimento concettuale utilizzato sopra, in base al quale il volume di uno strato di altezza dx è A(x) dx, e la sua massa è ρ g A(x) dx. Il peso della parte di torre compresa fra la quota x e l'altezza totale H della torre è:

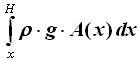
e, considerato il peso massimo che la struttura sottostante può reggere, vale 1'equazione:

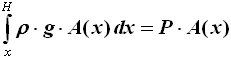
dove P è la pressione massima che può essere sopportata. Differenziamo entrambi i membri rispetto alla variabile x:

Quest'ultima si può riscrivere:

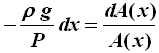
Integrando entrambi i membri tra 0 ed x si ottiene:

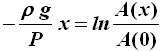
Da cui si ricava A(x), che è una funzione esponenziale:

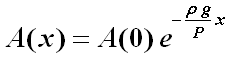
A(x) indica come varia la sezione orizzontale al variare dell'altezza x, e permette di ricavare il profilo della struttura, che può essere descritto dalla funzione del lato y della sezione al variare della quota, ossia dalla funzione:

Che rappresentata su un diagramma cartesiano appare così:

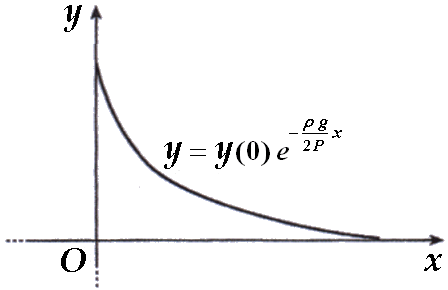
dove y(0) è il lato di base, pari alla radice quadrata di A(0). Come si vede, somiglia moltissimo al profilo della Torre Eiffel vista di lato! La sagoma di quest'ultima però non è esattamente esponenziale, perché 1'ingegner Eiffel non trascurò il soffiare del vento, che deve essere controbilanciato dalla tensione tra gli elementi della costruzione. Questo si traduce in un'equazione integrale non lineare molto complicata, le cui soluzioni forniscono la sagoma della struttura oggi visibile, esponenziale a tratti con due differenti esponenti. II monumento che vediamo oggi ha una base quadrata di 124,90 metri di lato (in altre parole, y(0) = 124,90 m), una dimensione notevole, perchè in un'epoca in cui non esistevano ancora i computer, Gustave Eiffel non era sicuro dei suoi calcoli, e preferì esagerare le dimensioni della base, in modo da essere certo che il vento non abbattesse la sua torre. Tra l'altro, quest'ultima avrebbe dovuto essere smontata al termine dell'Esposizione Universale, ma grazie al Cielo si decise di lasciarla al suo posto, dove la vediamo ancor oggi.

Aggiungiamo che la Torre Eiffel fu l'edificio più alto del mondo dal 1889, anno della sua costruzione, fino al 1930; nell'arco di soli due anni, l'edificio più alto del mondo fu costruito tre volte a New York: la Banca di Manhattan (oggi Trump Building) alta il 282,5 metri dall'aprile al maggio del 1930, il Chrysler Building alto 319 metri dal 27 maggio del 1930 al 1 maggio del 1931, e subito dopo l'Empire State Building alto 381 metri, sulla cima del quale è ambientato il kolossal "King Kong". Il 4 novembre 1972 il primato passò ai 416 metri delle Torri Gemelle del World Trade Center, sempre a New York, che già il 4 maggio 1973 ha lasciato spazio ai 443 metro della Sears Tower di Chicago (oggi Willis Tower). Ma era il canto del cigno dei primati a stelle e strisce: nel 1998 il titolo di edificio più alto del mondo passava alle Petronas Towers di Kuala Lumpur (Malaysia), alte 452 metri, e dopo un regno di sette anni il 14 novembre 2003 succedevano loro i 509 metri del Taipei 101 (Taiwan). Nulla però in confronto agli 828 metri della già citata Burj Khalifa a Dubai, che detiene il record dal 4 gennaio 2010. Ma c'è già chi si prepara a spodestare il colosso degli Emirati Arabi: la Sky City in progetto nella città cinese di Changsha si arrampicherebbe fino a 828 metri con ben 220 piani, e nel 2018 potrebbe iniziare la costruzione della King Tower a Gedda, in Arabia Saudita, che si propone di raggiungere la soglia psicologica dei 1.000 metri.

Questa gara ad arrampicarsi nei cieli potrà mai avere fine? Non nel prossimo futuro, almeno. Ma ci deve pur essere una sorta di punto di arrivo, un'altezza massima che un edificio può raggiungere. Ci sarà alla fine l'edificio più alto del mondo che sarà per sempre imbattibile? I progettisti di grattacieli vi diranno che ci sono molte limitazioni che impediscono alle moderne torri di Babele di salire sempre più in alto: materiali, comfort umano, tecnologia degli ascensore e, forse la cosa più importante, i soldi giocano un ruolo nel determinare l'altezza cui un edificio può o non può arrivare. Ma sicuramente ci devono essere alcune limitazioni fisiche che impediscono ad un edificio di andare troppo in alto. Abbiamo visto che non potrebbe esistere un edificio con un attico nello spazio, oltre l'atmosfera terrestre, come gli obelischi di Egira. Ma quanti chilometri potrebbe realisticamente diventare alto un grattacielo? Adrian Smith, l'architetto progettista dell'attuale edificio più alto del mondo e della futuribile King Tower di Gedda, ritiene che il problema predominante consista nel sistema di ascensori e di mezzi di trasporto. E l'ingegnere strutturale William Baker, che ha lavorato con Smith al Burj Khalifa, ha progettato il sistema che ha permesso alla torre di Dubai di salire così in alto, dei contrafforti a tre ali che consentono la stabilità senza che tutto lo spazio utilizzabile sia occupato dagli elementi strutturali. Egli si è spinto ad affermare: « Oggi si potrebbe facilmente erigere un palazzo alto un miglio e forse più. »

In effetti un edificio così alto dovrebbe essere vuoto internamente, proprio come la Torre Eiffel, per evitare il collasso dei piani inferiori che farebbe crollare gli obelischi di Greg Bear, ma dovrebbe anche avere una base enorme, per resistere al soffio del vento. Nel 1990 la Taisei Corporation ha concepito una supertorre a forma di vulcano che avrebbe dovuto sorgere non lontano da Tokyo, chiamata X-Seed 4000, di struttura non troppo dissimile da quella della Torre Eiffel e alta due miglia e mezzo, cioè 4000 metri, per un totale di 800 piani! Si pensi che il Monte Fuji, la cima più alta del Giappone, misura "solo" 3.776 metri. Esso potrebbe ospitare fino ad un milione di abitanti, e sarebbe stato realizzato con oltre tre milioni di tonnellate di acciaio rinforzato. Il fantascientifico progetto è finito in un cassetto a causa del crollo del mercato immobiliare alla fine degli anni 2000, e probabilmente anche per un po' di buon pragmatismo vecchio stile. Tokyo infatti si trova lungo il cosiddetto "Anello di Fuoco" del Pacifico, e la torre giapponese sarebbe esposta al rischio di terremoti e tsunami. Ripetendo i calcoli di Eiffel sopra descritti per l'X-Seed 4000, poi, si ottiene come risultato che la base di questa superstruttura dovrebbe essere un quadrato di 6 chilometri di lato! Per non parlare del costo stimato dell'opera, oltre mille miliardi di dollari.

Un edificio più alto di una montagna sembra un'idea assurda, ma secondo la maggior parte degli ingegneri oggi sarebbe del tutto possibile innalzarlo. Dal punto di vista tecnico sarebbe possibile anche elevare una torre alta 8.849 metri, cioè un metro più alta del Monte l'Everest, perché gli edifici sono di gran lunga più leggeri delle montagne, fatte di solido granito pieno: si stima che il volume del Burj Dubai sia occupato da circa il 15 % di elementi strutturali e dall'85 % di aria. Sulla base di un rapido calcolo, se un edificio pesa solo il 15 % di un obelisco pieno, potrebbe essere 6,7 volte più alto pur avendo il suo stesso peso. Questa salita di quota però avverrebbe a prezzo di una base sempre più ampia: estrapolando i calcoli dell'ingegner Eiffel, risulta che un edificio alto un metro più dell'Everest dovrebbe avere una base di ben 4.100 chilometri quadrati: un ingombro enorme per un edificio, anche uno con struttura per lo più cava. Conclusione della favola: purtroppo non posso darvi un numero tondo circa la massima quota che la mitica Torre di Babele potrebbe avere una volta per tutte: come la corsa fra le superpotenze alla costruzione dell'edificio più alto, così la stima della più elevata costruzione che l'ingegneria umana può concepire potrebbe aumentare da un giorno all'altro, sentendo il parere di qualche altro architetto ancora più ardito. Dopotutto, lo riconosceva lo stesso Signore Dio:

« Questo è l'inizio della loro opera e ora quanto avranno in progetto di fare non sarà loro impossibile! » (Gen 11, 6b)